The s-convexity of support functions of spherically convex sets

TAN Xue， GUO Qi

（School of Mathematical Sciences，SUST，Suzhou 215009，China）

Abstract： In this paper，we investigated the spherical support functions of s-convex sets，attempting to find their essential properties.For a given proper closed s-convex set，there is s-convex set decomposition on the domain of its s-support function，such that its s-support function is s-convex or s-concave on each component of such a decomposition.The results obtained here might be helpful in establishing a systematic spherical convexity theory.

Key words： spherically convex set；spherical support function；spherical convexity

1 Introduction

As known，the convexity of sets or functions in the Euclidean spaces plays an important role in various mathematics areas，such as analysis，geometry and optimization theory etc.In light of the success of convexity in linear spaces，it is natural to look for a systematic theory of convexity in the Euclidean sphere spaces.Actually，the attempt on this topic already appeared in the early 1920’s （see [1－2] and the references therein）.

Since 1940’s，various distinct definitions of convexity for sets in spheres have been proposed （cf.[1－4]）.All these convexities and the like were often called spherical convexity.Several equivalent definitions or necessary and suffcient conditions of these spherical convexities were given later （see，e.g.[3－6]）.We would like to point out that，among all these definitions，the one given in[4] or [6] is of its own feature：it is the only one given in the analytic form.

The earlier study on spherical convexity focused on combinatorial properties of spherically convex sets （with different definitions），such as，the theorems of Helly’s type （see，e.g.[2，7-9] and the references therein）.Then，the studies on other properties and applications of spherical convexity emerged gradually （see 3，10-13]）.Recently，the theorems of Radon’s type and Carathéodory’s type were established in [6].More interestingly，in [14]the concept of （spherically） convex function defined on the so-called weakly convex sets in a sphere was introduced and investigated systematically，e.g.as an application，necessary and suffcient optimality conditions for constrained convex optimization problems on the sphere are derived.The spherical minimax location problem was studied in [15-16].There are too many references to mention here.

Although some progresses have been made in the study on spherical convexity，the task to establish a systematic theory of spherical convexity is far away from being completed，simply because many counterparts of concepts and definitions for convex sets in Euclidean spaces have not been found for spherical convexity.So，in this paper，we make an effort to study the spherical support functions of spherically convex sets，attempting to find the essential properties of spherical support function.

2 Preliminaries

Rnand Sn-1denote the Euclidean n-space and the unit sphere in Rnrespectively.“〈·，·〉” and ||·|| denote the standard inner product and the norm induced by “〈·，·〉” on Rn，respectively.Often we also view Rnas an affine space，so we will not distinguish vectors and points intentionally.The origin（or zero vector） of Rnis always denoted by the letter o.R，R+and R*+stand for the set of reals，nonnegative reals and positive reals respectively.

For non-zero u∈Rnand α∈R，Hu，αdenotes the hyperplane {x∈Rn|〈u，x〉=α}.The sets of the form{x∈Rn|〈u，x〉＞α} andare called the open and the closed half space determined by u，α espectivelyare defined in a similar way）.In particular，when α=0，we write simply Hu，Hu+andinstead ofrespectively.A set of the form V∩Sn-1is called a k-sphere （0≤k≤n-1），where V is a （k+1）-dimensional subspace of Rn.Observe that a 0-sphere is of the form {x，-x} for some x∈Sn-1.A set of the formis called a closed （resp.open） hemisphereare defined in a similar way）.

Nonzero x，y∈Rnare called （a pair of） antipodes （or antipodal） if y=－x.For other notation refer to [17].

The radial projection ρ:Rn→Sn-1∪{o} is defined by

It is easy to check that the radial projection is of the following properties：

（i） ρ°ρ=ρ，where “°” denotes the composition of operators；

（ii） ρ（tx）=ρ（x），ρ（-x）=-ρ（x） for x∈Rnand t>0；

（iii） ρ（x）=x if and only if x∈Sn-1or x=o.

The spherical addition “+s” on Rnwas introduced in [4，6] as：x+sy:=ρ（x+y），x，y∈Rn.Clearly “+s” is a map from Rn×Rnto Sn-1∪{o}.And the spherically convex combination composition was also introduced in [4，6]：

For k≥1，x1，x2，…，xk∈Rnand nonnegative λ1，λ2，…，λkwith，define

called a spherically convex combination （an s-convex combination for brevity） of x1，x2，…，xk.Instead，（s）（λx+（1-λ）y） is often written as λx+s（1-λ）y.

Denote，for x，y∈Rn，[x，y]s:={λx+s（1-λ）y|0≤λ≤1}，which is a subset of Sn-1∪{o}.When x，y∈Sn-1（x=y is allowed） are not antipodal，[x，y]sis called the short arc connecting x and y （it can be checked easily that the short arc defined here coincides with the usual one defined in geometric languages），and [x，-x]s={o，x，-x} for x∈Sn-1.（x，y）s，（x，y]sand [x，y）sare defined in similar manners.

There are several distinct definitions for spherical convexity by different authors （see，e.g.[1－4，6] and the references therein），which lead to different families of spherically convex sets.We mention that all these definitions except the one in[4] or[6] are given in geometric languages.Here，we adopt the one given in [3]，but rewrite it equivalently in analytic languages （cf.[18]）.

Definition 1A set C⊂Sn-1is called spherically convex（s-convex for brevity） if for any w1，w2∈C and 0≤λ≤1，λw1+s（1-λ）w2∈C whenever λw1+（1-λ）w2≠o.

An s-convex set is called proper if it contains no antipodes.

Remark 1It was shown in [4，6] that if C is a proper s-convex set，then for any k≥1，（s）for all ui∈C，λi∈[0，1] with

We call an s-convex set closed if it is closed with respect to the usual Euclidean topology on Sn-1.The family of closed s-convex sets （called s-convex bodies usually） in Sn-1is denoted by K（Sn-1）.Clearly，all k-spheres and all closed hemispheres are in K（Sn-1）.The family of proper closed s-convex sets in Sn-1is denoted by Kp(Sn-1).It is easy to check that if Ci∈K（Sn-1），i∈I，then the nonempty intersection

The following fact mentioned without proofs in many papers （see.e.g.[3] and the references therein） was proved formally in [6].

Proposition 1Let s-convex C⊂Sn-1be proper.Then

（i） there is u∈Sn-1such thatis contained in a closed hemisphere.

（ii） if further C is closed，there are u∈Sn-1and α>0 such thati.e.C is contained in a closed cap.In particular，C is contained in an open hemisphere.

For C⊂Sn-1，define its radial hull as RC:=R+C，which is a cone.In [3]，C⊂Sn-1is defined as a spherically convex set if RCis convex，i.e.RC=coneC，the convex cone generated by C.This definition is equivalent to Definition 1 as shown in [6，18].The following facts were known and proved repeatedly by different authors （see，e.g.[6，18] and the references therein，or check directly）.

Proposition 2Let C⊂Sn-1.Then C=RC∩Sn-1and

（i） C is a （closed） s-convex set if and only if RCis a （closed） convex cone.

（ii） C is a proper s-convex set if and only if the convex cone RCis pointed，i.e.RC∩（-RC）={o}.

Thanks to Proposition 2，for an s-convex set C⊂Sn-1，we denote intC:=int（RC）∩Sn-1，riC:=ri（RC）∩Sn-1，bdC:=bd（RC）∩Sn-1，rbdC:=rbd（RC）∩Sn-1and clC:=cl（RC）∩Sn-1，called the interior，relative interior，boundary，relative boundary and closure of C respectively.

We need more preparations for the discussions in this article.

Definition 2[6，18]Let S⊂Sn-1.Then，the set

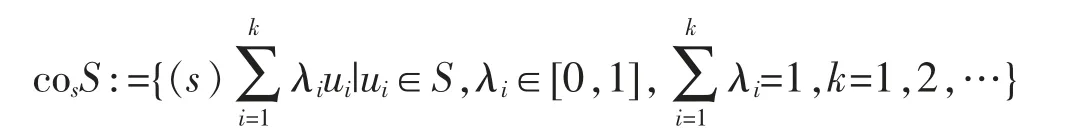
is called the spherically convex hull （s-convex hull for brevity） of S.

Remark 2By the spherical Carathéodory theorem shown in [6]，when S is contained in an open hemisphere，the k in Definition 2 can be limited in {1，2，…，n}.

Let C∈K（Sn-1）.A point w∈C is called an extreme point of C if u1，u2∈C and u=（1/2）u1+s（1/2）u2imply u1=u2=u.The set of extreme points of C is denoted by extsC.The following structural theorem of Minkowski type was shown also in [6].

Theorem 1Let C∈Kp（Sn-1）.Then extsC≠Ø and C=cos（extsC）.

3 Spherical support functions of s-convex sets

The support function of a convex body （i.e.a compact convex set） in Euclidean spaces is a crucial tool in convex geometric analysis：since a function on Rnis the support function of some convex body if and only if it is sub-linear，many nice properties and meaningful compositions of convex bodies can be derived/realized through their support functions.In light of these advantages，it is natural to look for the counterparts for closed s-convex sets in sphere spaces，including the definition of spherical support functions and their essential characteristics.There are already some attempts on this topic.Here we discuss the one introduced in [10] or [19] （see the references therein for more information）.

To define and study the spherical support functions of s-convex sets，some more notation and preparations are needed.The spherical （or intrinsic） distance ds（u，v） between u，v∈Sn-1is defined as ds（u，v）:=arccos〈u，v〉.It is easy to check that ds（·，·） is indeed a metric on Sn-1，and 0≤ds（·，·）≤π.Moreover，ds（u，v）=0 if and only if u=v，and ds（u，v）=π if and only if u=-v.As usual，for u∈Sn-1，S⊂Sn-1，denote ds（u，S）:=inf{ds（u，w）|w∈S}，called the distance between u and S.We point out also that the intrinsic distance and the Euclidean distance are equivalent on Sn-1.

Let SV:=V∩Sn-1be a k-sphere （0≤k≤n-1）.Then，the spherical projectionis traditionally defined （see [3] or [19]） by

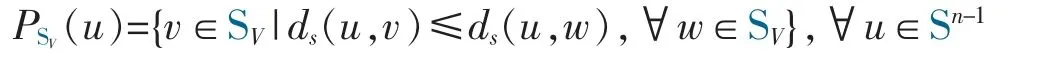
Definition 3Let SV:=V∩Sn-1be a k-sphere and PVbe the orthogonal projection from Rnto V.Then the map PSV:Sn-1→P（SV） defined by

is called the spherical projection from Sn-1to SV，where kerPVdenotes the kernel of PV.

In terms of Definiton 3，we can easily show that the spherical projection is s-convexity-preserving （see [18]for more general conclusions）.

Theorem 2Let SV:=V∩Sn-1be a k-sphere.Then for each (closed) s-convex set C⊂Sn-1，SVis （closed） s-convex.Moreover，if C is proper and C∩kerPV=Ø，then so is PSV（C）.

Proof.We discuss the the closedness-preserving property first.If C∩kerPV≠Ø，then PSV（C）=SVis closed clearly.If C is closed and C∩kerPV=Ø，then PSV（C） is closed by the continuity of ρ and PVand by the compactness of C.

Next，we consider the s-convexity.If C∩kerPV≠Ø，then PSV(C) is s-convex trivially.Now，assume C∩kerPV=Ø.Let u1，u2∈PSV（C） and λ∈[0，1].Then u1=PSV（w1） and u2=PSV（w2） for some w1，w2∈C.If λu1+（1-λ）u2≠o，then λw1+（1-λ）w2≠o，and so

Facing the child s clear and glistening4（） eyes, the hostess was stupefied, leaning on the door feebly（） and holding her face with two hands, afraid to look him in the eye.

Finally，since for w1，w2∉kerPV，PSV（w1）=-PSV（w2） implies w1=－w2（which can be checked easily），we see that PSV（C） contains no antipodes if C contains no antipodes and C∩kerPV=Ø.

Now，we recall the definition of spherical support functions for proper closed s-convex set.For v∈Sn-1，denote Sv:=Hv∩Sn-1（a （n-2）-sphere），Sv+:=Hv+∩Sn-1（an open hemisphere） and（a closed hemisphere）.Then write Kp（Sv+）:={C⊂Sv+|C is a closed s-convex set} （observe that every C∈Kp（Sv+） is automatically proper）.

Definition 4[19]Let v∈Sn-1，C∈Kp（Sv+）.Then the spherical support functionof C is defined by

where “sgn” is the sign function and S（u，v）:=lin{u，v}∩Sn-1，where lin{u，v} is the linear subspace generated by the set {u，v}，denotes the unique great circle containing u，v.

Remark 3By the compactness of PS（u，v）（C），for each u∈Sv，there is w0∈C such that

Theorem 3Let v∈Sn-1，C∈Kp（Sv+）.Then，for each u∈Sv，there is w∈extsC such that

To prove Theorem 3，we need the following lemmas.

Lemma 1Let C1be a proper s-convex set，f:C1→R be an s-convex function and PSV:Sn-1→Svbe the spherical projection.If C2is s-convex and PSV（C2）⊂C1，then for any m≥1，wi∈C2，λi∈[0，1]，1≤i≤m，withthere exist μi=μi（w1，…，wm；λ1，…，λm）∈[0，1]，1≤i≤m，withsuch that

Proof.We point out first that C2has to be proper in this case since PSVmaps antipodes into antipodes and C1contains no antipodes.Let w1，w2，…，wm∈C2and λ1，λ2，…，λm∈[0，1] withDenoting（observingand PV（wi）≠o），we have

The proof is complete.

Lemma 2For any u∈SVand w∈SV+，〈u，PV（w）〉=〈u，w〉 and 〈v，PV（w）〉=〈v，w〉，where V:=lin{u，v}，and so

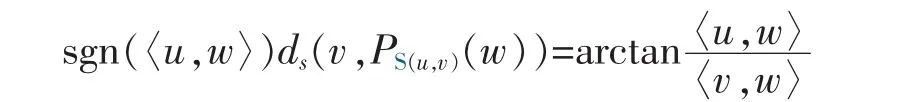
Proof.Since PV（w）=〈v，w〉v+〈u，w〉u，we have

where we used the facts that 〈u，v〉=0 and 〈u，u〉=〈v，v〉=1.Thus，

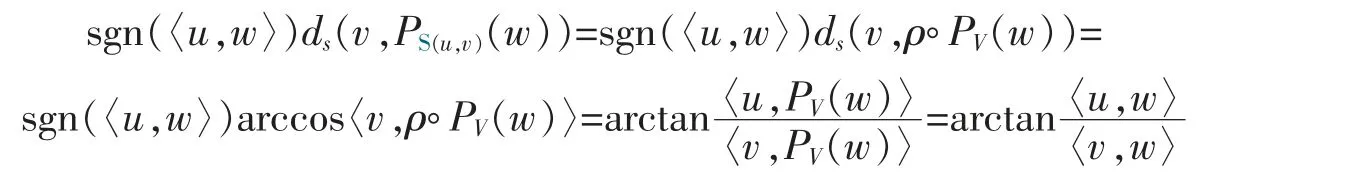
Proof of Theorem 3Consider the case hv（C，u）≥0 first and denoteThen by the definition of hv（C，·） and Lemma 2 （observing that 〈u，PV（w）〉≥0 iff 〈u，PS（u，v）（w）〉≥0），C2is a nonempty proper closed s-convex set in the case hv（C，u）≥0.Now，consider the s-convex function f（·）:=ds（v，·）on C1（see [14] for the s-convexity of such an f）.Observe also that in this case，

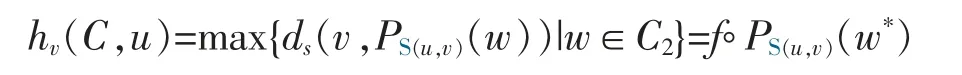
for some w*∈C2.

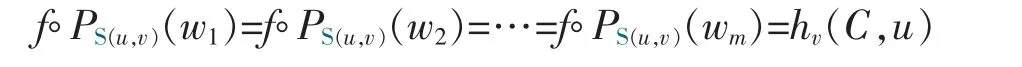
i.e.ds（v，PS（u，v）（wi）=hv（C，u） for 1≤i≤m.

Now，if hv（C，u）>0，then wi∉C∩Husince ds（v，PS（u，v）（w））=o for all w∈Hu∩Sv+.So，it is easy to see that wi∈exts（C）.If hv（C，u）=0，then，whereand:={x∈Rn|〈u，x〉≤0}，and hv（C，u）=PS（u，v）（w） for all w∈C∩Hu=C∩Su，in particular，for all w∈exts（C∩Su）（notice that C∩Suis clearly a proper closed s-convex set and so exts（C∩Su）≠Ø by Theorem 1）.Next，we show that exts（C∩Su）⊂extsC：

Let w∈exts（C∩Su） and w1，w2∈C，λ∈（0，1） with λw1+s（1-λ）w2=w.Then

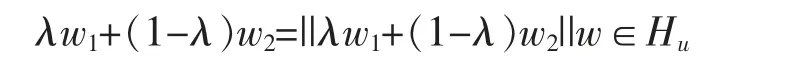
which leads to w1，w2∈Husince Huis a face ofand in turn w1，w2∈C∩Su.So，w1=w2since w∈exts（C∩Su）.Thus，we confirmed w∈extsC.

For the case hv（C，u）<0，takeandThen g is s-convex on Su-and hv（C，u）=max{PS（u，v）（w）|w∈C}（observing C⊂Sv+∩Su-in this case）.Thus，the same argument as above works well.

4 S-convexity and s-concavity of s-support functions

As mentioned previously，the support function of compact convex sets plays an important role and the sublinearity is its crucial property.It is reasonable to look for the crucial properties of s-support functions.This is clearly an important and a tough problem at same time.However，we have known almost nothing about this topic.

In this section，we try a little more to understand the s-support functions through its s-convexity or s-concavity.

Given C∈Kp（Sv+）.For w*∈bdC，denote Cv（w*）:={u∈Sv|hv（C，u）=sgn（hv（C，u））ds（v，PS（u，v）（w*）}.Then，we have the following conclusion first.

Theorem 4Let C∈Kp（Sv+）.Then Cv（w*）（⊂Sv） is a non-empty closed s-convex set for each w*∈bdC.

Proof.Let w*∈bdC.Then w*∈bdRCby the definition and further there is a hyperplane Hu*supporting RCat w*，where u*∈Sn-1is chosen so that（Theorem 3.1.9 in [17]）.Now，let u be the （only） intersect point ofWe shall show u∈Cv（w*）：by the choice of u，lin{v，u*}=lin{v，u}=:V.By Lemma 2，for all w∈C，〈u*，PV（w）〉=〈u*，w〉≤0 sinceand in turnWith the fact w*∈Hu*，an elementary geometric argument leads to sgn（hv（C，u））ds（v，PS（u，v）（w*））＝hv（C，u），i.e.u∈Cv（w*）.

Next，we show that Cv（w*） is s-convex.First，for u1，u2∈Cv（w*） with u2≠-u1and λ∈（0，1），denoting u¯λ:=λu1+（1-λ）u2and uλ:=λu1+s（1-λ）u2，we have by Lemma 2，for any w∈Sv+，

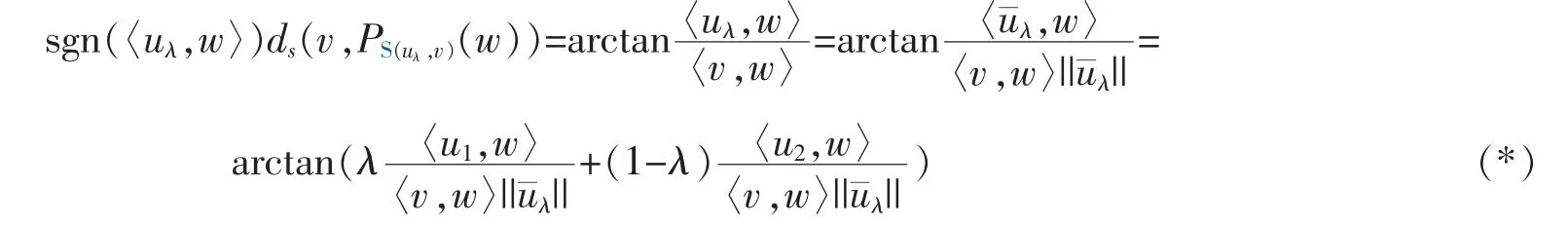
Thus，let hv（C，uλ）=sgn（〈uλ，w′〉）ds（v，PS（uλ，v）（w′）） for some w′∈C.By definition，we have

If sgn（〈uλ，w′〉）ds（v，PS（uλ，v）（w′））>sgn（〈uλ，w*〉）ds（v，PS（uλ，v）（w*）），we would have by （*）

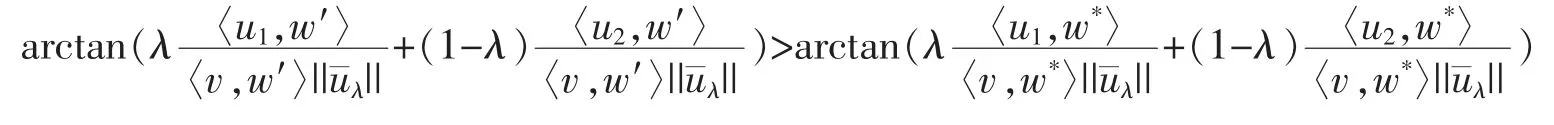
which leads to

This inequality implies that at least one of

holds.So，by Lemma 2 again，at least one of

holds，a contradiction.So，hv（C，uλ）=ds（v，PS（uλ，v）（w*）），i.e.uλ∈Cv（w*）.

Finally，the continuity of hv（C，·） and sgn（〈·，w*〉）ds（v，PS（·，v）（w′）） ensures the closedness of Cv（w*）.The proof is complete.

From Theorem 3 and Theorem 4，we have immediately the following decompositions of a sphere through closed s-convex sets.

Proposition 3Let C∈Kp（Sv+）.Then

The next theorem shows the s-concavity of s-support functions on some s-convex sets and indicates at the same time the value of Proposition 3.

Theorem 5Let C∈Kp（Sv+）.Then，for each w∈bdC，hv（C，·） is s-concave on Cv+（w） and s-convex on Cv-（w），where Cv+（w）:={u∈Cv（w）|〈u，w〉≥0} and Cv-（w）:={u∈Cv（w）|〈u，w〉≤0} are closed s-convex sets.

Proof.Let u1，u2∈Cv+（w） and λ∈[0，1].Denoting uλ:=λu1+s（1-λ）u2and:=λu1+s（1-λ）u2，we have uλ∈Cv（w） by Theorem 4，and 〈uλ，w〉=||||-1（λ〈u1，w〉+s（1-λ）〈u2，w〉≥0）.So uλ∈Cv+（w） and Cv+（w） is s-convex.The closedness of Cv+（w） is straightforward.Similarly，the same argument works well for Cv-（w）.

Observe that，for u1，u2∈Cv（w） and λ∈[0，1]，we have，by （*） in the proof of Theorem 4

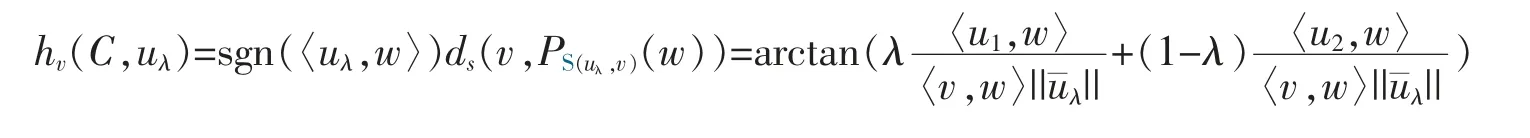
So，if u1，u2∈Cv+（w），then

since the function arctant is increasing and concave on [0，+∞），where we used the fact that

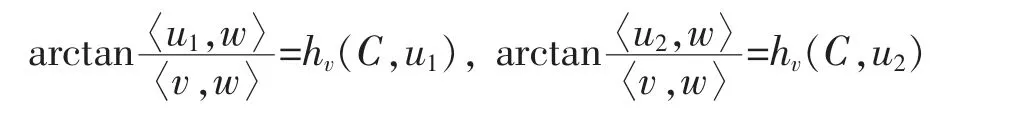
by （*）.

Similarly，if u1，u2∈Cv-（w），then

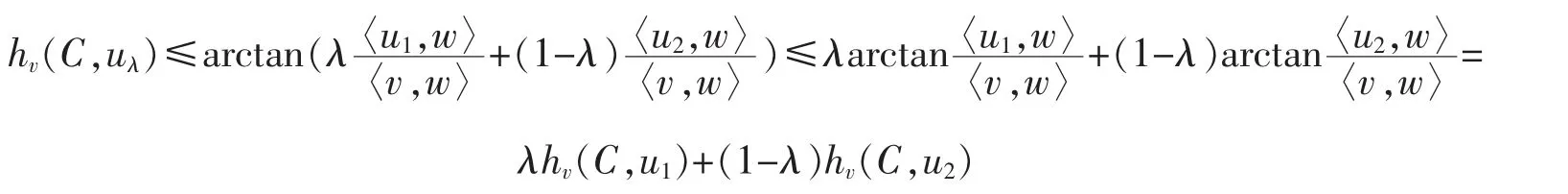
since the function arctant is increasing and convex on （-∞，0].

In practice，we often choose v∈C so that hv（C，u）≥0 for all u∈Sv，which implies that，for each w∈bdC，〈u，w〉≥0 for all u∈Cv（w）.Hence，by Proposition 3 and Theorem 5，we have the following corollary concerning with spherical polytopes.

Corollary 1Let C=cos{v1，v2，…，vm}∈Kp（Sv+） and v∈C.Then there exist closed s-convex sets D1，D2，…，Dk（k≤m） such thatand hv（C，·） is s-concave on each Di.

Proof.Sinceby Proposition 3 and Theorem 5 the proof is finished as long as we denote Di:=Cv（vji），1≤i≤k.

Final RemarkIn this article，we study the s-convexity and the s-concavity of the s-support functions，trying to find the key properties of the s-support function.Even if the outcomes are not as satisfactory as we hoped，there is still some progress in this direction.We will continue such an investigation to this topic in the future.