基于EMD 分解的MEMS 加速度计随机误差补偿

田易 李继秀 钟燕清 阎跃鹏 孟真 张兴成

(1.中国科学院微电子研究所,北京 100029;2.中国科学院大学,北京 100049)

0 引言

MEM S加速度计是惯性导航系统中的核心器件之一,其测量精度直接影响惯性导航系统的导航及姿态测量精度,因此需要对M E M S 加速度计数据进行随机误差补偿,提高其测量精度。

目前关于陀螺随机误差降噪方法已经有了广泛深入的研究, 包括基于多尺度小波变换[1]的方法、基于A R M A 建模的卡尔曼滤波[2]等方法。但由于小波分解参数具有非自适应性,不适用于时变信号[3],而A R M A 建模需要信号满足线性、平稳性的要求,因此限制了其应用。EMD方法于1998年由Huang N.E.提出[4],是一种新型的信号分解方法,在非线性、非平稳信号的处理中具有良好的效果[5]。本论文将基于EMD分解的滤波算法应用于加速度计数据降噪,实现提高加速度计测量精度的目的。

1 基于EMD分解的随机误差补偿

Huang等人针对非平稳信号提出了一种经验模态分解的信号处理方法，该方法基于以下的设定：

（1）被分析信号至少包含极大值和极小值两个极值点；

（2）根据两个相邻极值点的时间距离定义固有振荡模式的特有时间尺度。对信号x(t)进行EMD分解过程如下。

步骤1：确定原序列x(t)的全部极大值和极小值点，利用三次样条函数分别把它们拟合为该信号的上下包络线，计算两包络线的均值m1，进而求出m1和x(t)的差值h1，h1=x(t)-m1，判断h1是否满足IMF的两个条件：

（1）整个数据序列的极大极小值数目与过零点数目相等或最多相差一个；

（2）数据序列的任意点上，由极大值确定的包络与由极小值确定的包络的均值始终为0，即信号关于时间轴局部对称。

若满足，则令其为x(t)的第一个IMF成分IMF1，IMF1=h1，并求出原信号x(t)与该IMF1的差值r1，r1=x(t)-IMF1。

步骤2：若h1不满足I M F 条件，则将h1视为新的信号序列，重复步骤1，重复上述过程n 次，直至满足I M F 条件，并令其为x(t)的第一个IMF成分IMF1，并求出原信号x(t)与IMF1的差值r1=x(t)-IMF1。把r1当作一个新的“原始”序列。

步骤3：重复步骤1 ～2，逐次提取出I MF2、I MF3、…、IMFn，其中rn=rn-1-IMFn，当rn变成一个单调序列，则完成E MD 分解，rn是原始信号的余项或者趋势项。

基于E M D 分解的加速度计随机误差补偿算法首先通过EMD分解后,将加速度计信号分解为多个IMF和一个趋势项,满足:

通过连续均方误差分析及计算IMF与原始信号的l2阶范数将IMF分为噪声主导IMFs、噪声/信号混合IMFs和信号主导IMFs。对于噪声IMFs直接去除,混合IMFs采用阈值滤波,将滤波后结果与信号主导IMFs和残留趋势项一起进行信号重构,得到降噪后的加速度计信号。

1.1 噪声主导的IMFs与混合IMFs的区分

本文采用CMSE的方法来区分噪声主导的IMFs与混合IMFs,首先,依次递增选择IMFs重构信号如下:

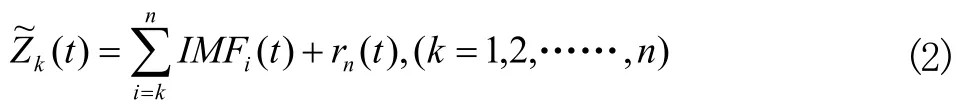
然后,计算两个连续重构信号的C MS E 值如下:

则噪声主导的IMFs与混合IMFs的区分参数M1可由下式得出:

1.2 信号主导的IMFs与混合IMFs的区分

本文采用l2范数方法计算信号与I M F 的P D F 之间的距离来确定信号主导的IMFs与混合IMFs。设两组数据的P D F 的值分别为P与Q,则l2范数计算公式如下所示:

图1 降噪前后加速度信号Fig.1 Acceleration signal before and after noise reduction

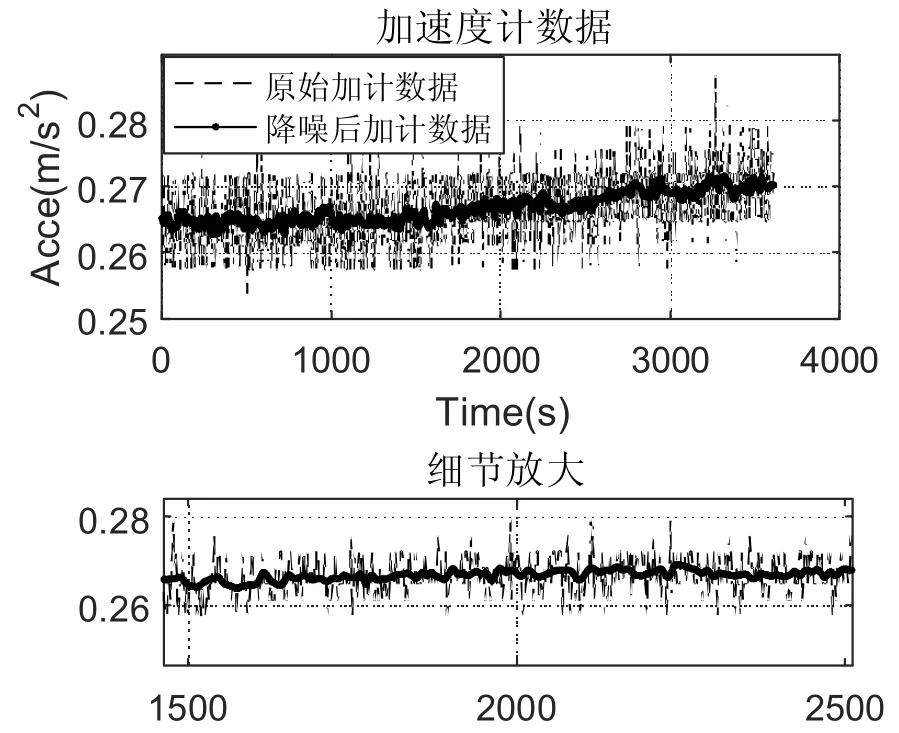
图2 实采加速度计信号降噪前后对比Fig.2 Comparison of real accelerometer signal before and after noise reduction

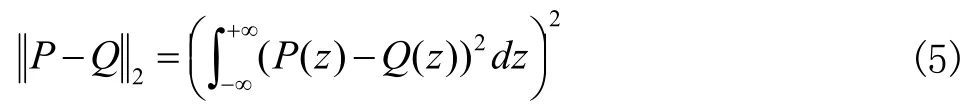
通过PDF表示的原始信号与每个IMF之间的相似性度量具有以下形式:

其中“dist”表示通过l2范数计算两个PDF的距离。信号主导的IMFs与混合IMFs的区分选择规则是D(i)的局部极大值之后的一个IM F所对应的阶数。

1.3 基于软阈值滤波的混合IMFs降噪

采用EMD-SIT法实现混合IMFs的降噪,利用两相邻过零点区间与过零点区间内的极值信息建立基于两相邻过零点区间与区间内极值的阈值滤波规则,另IMF中两相邻的过零点为,消噪方法为:

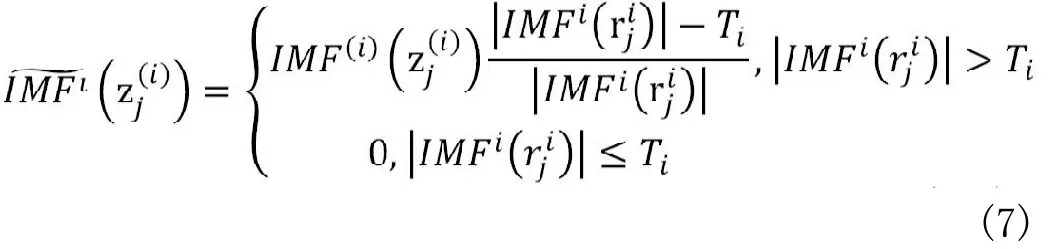
对每一个IMF系数采用固定的阈值进行去噪,第i个IMF的阈值定义如下:

其中σi表示噪声方差,通过中值估计法得到:

其中,Median为取中值运算,IMF(i)(t)表示第i个IMF。

2 仿真动态数据验证

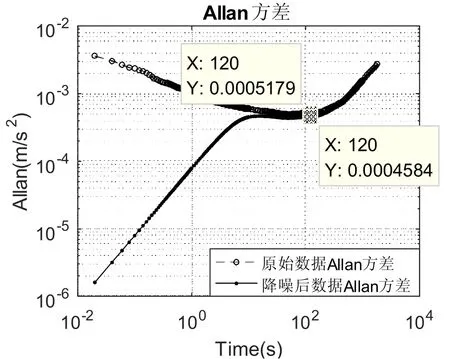
图3 滤波前后Allan 方差对比Fig.3 Comparison of Allan variance before and after filtering

仿真生成加速度计数据,使敏感轴分别处于水平、向上和向下位置,并添加均方差为0.5的白噪声。采用文中方法对加速度计数据进行降噪,与原始信号对比如图1所示,使信号噪声的均方差由0.498降低到0.101,数据噪声降低了79.7%。

3 实采静态数据验证

以50Hz采样率,采集1h加速度计数据,通过基于EMD分解的随机误差滤波方法,实现对加速度计数据的滤波降噪, 对比结果如图2 所示。并对滤波前后的数据进行Allan方差分析,加计的零偏稳定性由0.053mg(5.18e-4m/s^2)降低至0.047mg(4.58e-4m/s^2),同时大幅度降低了加速度计中的随机游走误差,有效提高了加速计的测量精度,对比结果图3所示。

4 结语

采用一种基于E M D 分解的滤波降噪方法, 可以对M E M S 加速度计的随机误差进行滤波消除,有效降低加速度计随机噪声对测量精度的影响。本文首先对加速度计的数据进行了EMD 分解,得到若干个本征模态函数和一个残余分量,将IMF分量分为噪声主导分量、信号/噪声混合分量及信号主导分量三类,通过阈值处理实现信号/噪声混合分量降噪;将经过降噪的信号/噪声混合分量与信号主导分量进行重构,得到降噪后的加速度计信号。通过仿真动态数据验证,使信号噪声的均方差由0.498降低到0.101,数据噪声降低了79.7%;通过实采静态数据验证,可将加速度计的零偏稳定性由0.053mg(5.18e-4m/s^2)降低至0.047mg(4.58e-4m/s^2),同时大幅度降低了加速度计中的随机游走误差,有效提高了加速计的测量精度。