计算机视觉中双目测距系统研究

李宏伟，崔羊威，张贺磊

（1.漯河职业技术学院，漯河462000；2.郑州航空工业管理学院，郑州450046）

近年来随着计算机技术发展，更多研究学者和公司开始着手于人工智能技术的研究和应用。以机器视觉中双目测距系统为研究对象，搭建一套双目视觉系统进行测量；利用MATLAB和OpenCV平台工具，先采集20对棋盘格图像进行摄像机的标定，再利用标定结果进行立体校正，运行BM、SGBM、GC和SIFT四种算法，分别对它们进行测距计算；结果表明，错误率分别是5%、3.6%、2.4%和4.1%，准确率都很高，都表现出较好的测量性能。

人工智能；机器视觉；测距；OpenCV；错误率

0 前言

近些年来，在世界范围内软件和硬件技术都有着很大的发展和突破，使很多科学理论研究变为现实为可成。19世纪50年代的模式识别[1]，它是让计算机使用数学的思想方法去解决模式（环境与客体）的分析处理问题；再到近十年来被人们广泛谈起的人工智能，让机器具有人类思维去分析处理现实中的问题。很多研究学者都认为模式识别技术就是早期的人工智能。人工智能有着广泛的应用范围，其中机器视觉[2]是它很重要的一个分支方向。机器视觉在无人驾驶[3]、电力巡检[4]、物体尺寸测量[5]、车牌识别[6]、农业果蔬采摘[7]等众多领域有着广泛应用。等本文选择一个双目摄像头，搭建了双目测距系统平台，利用MATLAB与OpenCV工具[8]，对实验过程中的数据进行处理分析，最后通过结论验证实验数据的准确性和可靠性。

1 双目视觉测距理论介绍

所谓的双目测距系统[9]，简单地说就是在自然的真实场景中，采用一个摄像头在不同的位置采集两张图像或者使用双目摄像头采集两张图像。然后将这两张图像通过相应的计算机视觉图像算法处理，便可得到所需的数据结果。双目测距系统主要是由双目立体匹配和测距计算两个部分组成的[10]。其中双目立体匹配技术的研究分析一直是研究学者近些年来探究的热点[11]，它又可以分为基于区域的和基于全局的。测距的计算部分是在立体匹配算法得到视差图后，通过测距数学模型进行的数据计算和分析[12]。

如图1，在理想情况下，左摄像头的中心O1与右摄像头的中心Or位于同一水平线上，O1Or称为基线b，都位于三维坐标系OaXaYaZa中。其中，Zl、Zr分别是左摄像头与右摄像头的光轴，二者是相互平行的，且在空间位置上分别垂直于三维坐标系中的Xa轴。三维坐标系中任意一点P在左右摄像机成像平面上的映射点分别是点Pl、点Pr，点P、点Pl、点Pr、点O1、点Or这5这个是共面的，这个平面与左右两个摄像机成像平面两条相交线分别称为左极线与右极线[13]。

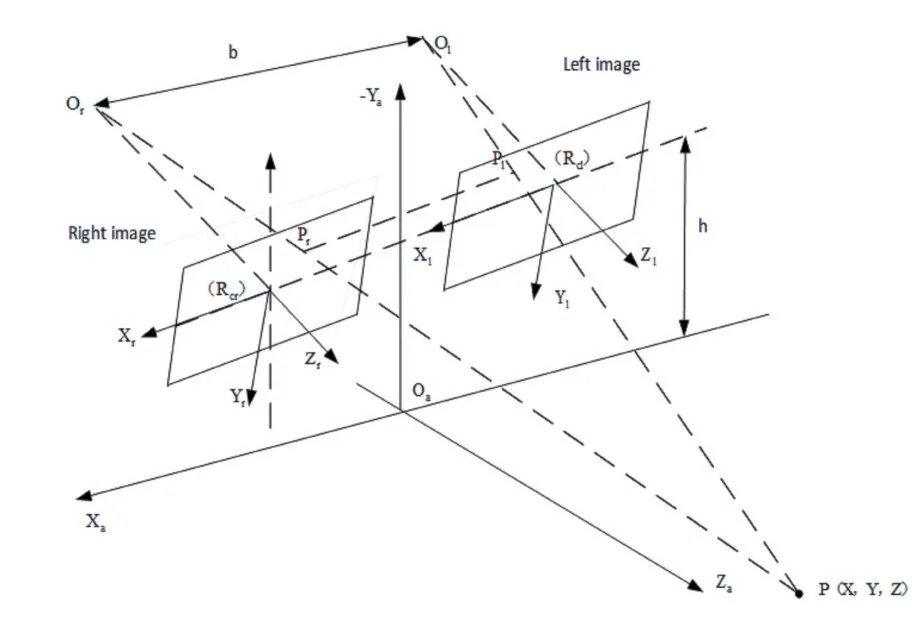
图1 双目立体系统

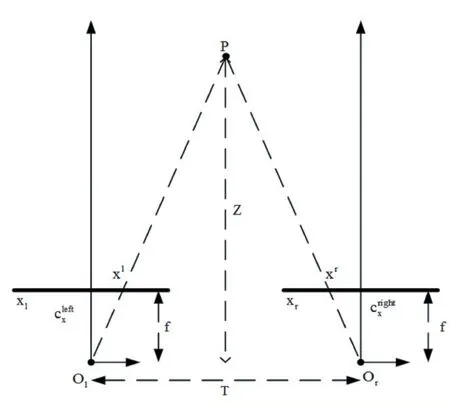
图2 测距原理

如图2，假设我们的摄像机是前向平行排列的[14]，也就是左摄像机每一个像素行与右摄像机的每一个像素行相互准确对齐的。点P是物理世界中任意点，Pl是左图像上的成像点，横坐标为xl；Pr是右图像上成像点，横坐标为xr。在这种理想情况下，我们得到视差与深度（距离）成反比，其中视差被简单定义为d，再利用三角形相似我们可以得到如下式子：

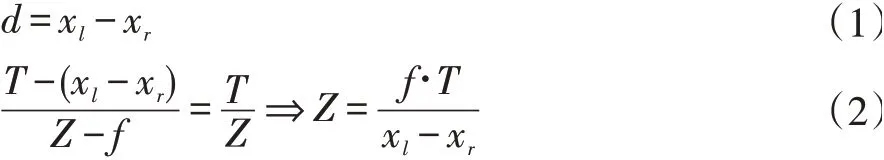
通过以上对测距系统主要内容的介绍，我们可以得到本文中算法的流程图如图3所示。

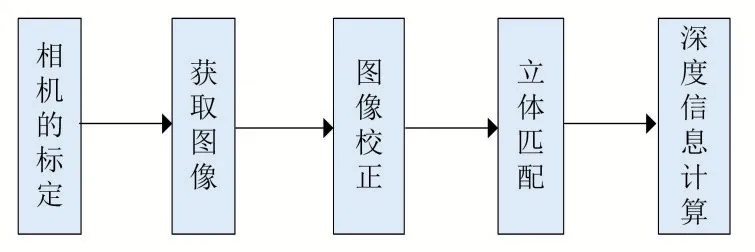
图3 测距系统流程图

2 实验过程

2.1 摄像机的标定

在摄像机的标定部分，目前来说主要有MATLAB和OpenCV两种工具可以选择。在MATLAB中又有MATLAB标定工具箱和手动标定TOOLBOX_calib两种方法，我们选择使用标定精度比较高的TOOL⁃BOX_calib工具箱进行摄像头的标定[15]。下图是我们使用双目摄像头采集到的20对棋盘格标定图像，尽量使每一对图像都有不同的姿态，这样我们的标定结果越准确。

图4 20对棋盘格图像

左摄像机参数如下：

选择使用非线性优化方法法对投影误差进行最小化操作，得到优化后数据：

焦距：

fc=[484.81152 483.18178]±[2.32920 2.35419]

图像中心点：

cc=[307.04251 229.27620]±[2.09426 1.54072]

相机两坐标轴夹角：

alpha_c=[0.00000]±[0.00000]→angles of pixel axes=90.00000±0.00000 degree

畸变：

kc=[0.09218- 0.08036 0.00389- 0.00313 0.00000]±[0.00991 0.02505 0.00122 0.00000 0.00000]

对右摄像机进行同样的处理，得到其参数如下：

选择使用非线性优化方法法对投影误差进行最小化操作，得到优化后数据：

焦距：

fc=[488.64709 487.20682]±[1.78000 1.83256]

图像中心点：

cc=[297.32973 231.38645]±[1.80916 1.41391]

相机两坐标轴夹角：

alpha_c=[0.00000]±[0.00000]→angles of pixel axes=90.00000±0.00000 degree

畸变：

kc=[0.07817-0.04069 0.00334-0.00168 0.00000]±[0.00932 0.03458 0.00117 0.00000 0.00000]

先分别对两个相机进行单目标定，再使用立体标定工具箱(Stereo Camera Calibration Toolbox)进行立体标定。选择使用左相机坐标系作为世界坐标系，求出相机间的旋转矩阵R和平移向量T：

2.2 真实场景图像采集

本文利用双目摄像头对真实场景中的图像进行采集，随机选择水杯盒子距离摄像头300mm的图像，如图5所示。

图5 300mm真实场景图像

3 实验数据分析

本文分别在水杯盒子距离摄像头200mm、300mm、400mm、500mm距离处，在每个距离点都采集5张图像，共采集20张图像，在每一张图像中选择同一平面上距离相等的10个点进行求均值作为最终距离。使用MATLAB中我们标定的摄像机参数，利用的BM、SGBM、GC[16]和SIFT[17]这四种算法，对实验结果数据进行记录并分析，所得结果如表1。

图6 SIFT角点匹配图

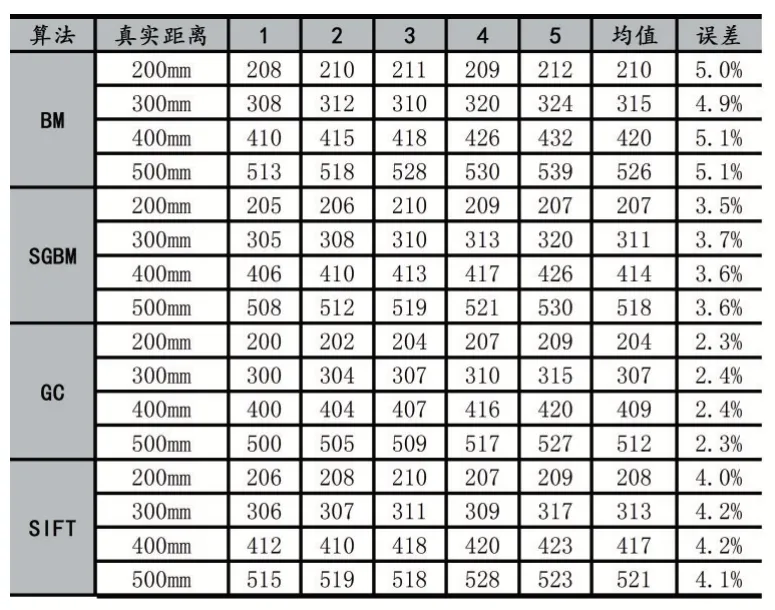
表1 BM、SGBM、GC、SIFT测距数据

从表1中的误差可以看出：BM算法的精度为5.0%，GC算法的误差为2.4%，SIFT角点匹配算法和SGBM算法表现居中，误差分别为4.1%和3.6%。

4 结语

本文在双目视觉系统的基础上，介绍了双目测距的原理，结合OpenCV和MATLAB工具，对BM、SG⁃BM、GC、SIFT四种算法的精度进行比较分析。一般来说，双目立体匹配算法越精确，在最后的测距计算部分越准确。在今后的研究学习过程中，我们可以继续研究双目立体匹配算法优化上来，得到更加准确的视差图；也可以往实时的双目立体技术进行研究，应用到具体的工程项目中去。