利用空间分布熵的改进VLAD图像检索
2021-03-23孙明思赵宏伟赵浩宇王也然
孙明思,赵宏伟,赵浩宇,王也然
(1.吉林大学计算机科学与技术学院,吉林长春130012;2.吉林农业科技学院电气与信息工程学院,吉林吉林132101;3.吉林大学符号计算与知识工程教育部重点实验室,吉林长春130012;4.吉林大学学报(工学版)编辑部,吉林长春130012)
1 引 言
互联网应用的普及产生了大量的图像信息,如何快速准确地检索到所需图像,是亟待解决的技术问题,也是目前图像检索领域的研究热点[1]。在图像检索的过程中,需要提取图像的特征,通过图像特征的比对,实现图像的识别与分类,所以在图像检索的各种方法中,图像特征占有重要地位,也是图像识别与分类的重要依据。不同的图像检索方法提取的图像特征有所不同。尺度不变特征变换(Scale Invariant Feature Trans⁃form,SIFT)描述子[2]是一种应用比较广泛的图像特征,在对SIFT描述子的进一步研究中,产生了局部聚集描述子向量(Vector of Aggragate Locally Descriptor,VLAD)[3]、词袋模型(Bag of Words,BOW)[4]等新的特征描述子。
SIFT是由Lowe提出的。SIFT描述子通过检测图像兴趣点来选择图像标识的稳定的关键点,并进一步确定关键点方向,形成关键点梯度描述特征向量。在图像识别的过程中,对检测图像按照同样的方法产生特征向量描述子,并进行特征匹配,进而实现图像目标检测的目的。SIFT描述子稳定性好,并具有图像尺度、旋转的不变特性[5]。
BOW是一种词袋模型,早期用于信息检索领域,引入计算机视觉领域后用于图像分类。BOW方法把图像块的特征向量作为“单词”,用直方图的方式统计单词出现的频率。在BOW方法中,图像块的特征向量可以采用SIFT描述子表达[6],对图像训练集中的全部图像进行SIFT特征提取,获得特征点的SIFT描述子,然后采用K均值聚类算法(K-means clustering algorithm,K-means)方法[7-8]对SIFT特征进行聚类,得到相应的聚类中心,由这些聚类中心构成词典,其中的聚类中心就是“单词”。每一个新的特征点都会映射到某一个聚类中心之上。如果把聚类中心点的个数作为横坐标,把相应聚类中心中特征点的个数作为纵坐标,就会得到一个图像特征的概率直方图,从而形成一个图像的一维的BOW向量,以此实现图像的检索。对比于SIFT图像特征,BOW算法的图像特征复杂度更低,图像特征维度也更低,所以,在图像检索效率方面有更好的表现,但是,在某些应用场景,图像检索准确率表现得不够好,借助于VLAD,则在BOW的基础上可以有效提升图像检索的准确率。
VLAD算法在图像初期处理时与BOW算法基本相同,采用K-means算法对SIFT特征进行聚类,得到相应的聚类中心,采用最近邻方法方法(Nearest Neighbors,NN)[9]将新的特征描述子映射到聚类中心,与BOW算法不同的过程在于,VLAD算法需要获得一个聚类中心VLAD值,这个聚类中心VLAD值由聚类中心全部残差之和组成。图像VLAD值由全部聚类中心VLAD值组合表达。
分析VLAD特征向量的形成过程,可以发现该方法存在的问题:VLAD特征向量是一个累加残差,是由各个SIFT描述子与聚类中心的差值累加得到的结果,这一结果可能导致不同的图像具有相同的累加残差,降低了依据VLAD特征向量识别图像的能力。分析出现这种情况的原因,主要是VLAD算法侧重提取描述子特征表达的具体数值,没有考虑相关的图像空间信息。如果VLAD特征向量能够融合描述子空间信息,将有效改善上述情况。一些现有的算法针对这一问题也做了一些改进,但主要体现在补充信息上,这种补充信息加大了向量维度,从而降低了图像检索效率。本文提出的方法结合了信息熵方法,维度低,节省内存占有量,且有效提高了图像检索效率和准确度。
2 算法原理
2.1 VLAD特征
VLAD算法采用非监督式的K-means聚类方法进行训练[10]。聚类中心记为ci,i表示聚类中心的编号,i={1,2,…,k},k表示聚类中心的个数,预先设定。一个SIFT描述子记为si,j,i表示这个描述子所在聚类中心的编号,i={1,2,…,k},j表示这个描述子在该聚类的编号,j={1,2,…,mi},mi表示第i个聚类中心具有的SIFT特征的个数,这种标记可理解为:si,j是聚类中心ci所属聚类中的一个描述子,编号为j,聚类中心ci所属聚类中有多个描述子,最大描述子编号为mi。
采用NN最近邻方法把一个图像SIFT特征描述子si,j划归到一个聚类中,按照NN最近邻方法思想,这个聚类就是ci所属的聚类,而ci就是这个聚类的聚类中心。之后,计算每一个聚类中的残差,残差ri,j可以通过式(1)计算得出:

因为ci是由si,j进行聚类训练求得,所以两者具备相同的维度。si,j是SIFT描述子,可表示为一个128维的向量,同样,ci也可表示为一个128维的向量,在计算残差时,按照对应的向量维度进行减法操作,即可得到一个128维的ri,j残差向量。
在一个聚类中,每一个SIFT描述子按照公式(1)与该聚类的聚类中心ci进行差值计算后,都可以获得一个残差,mi个SIFT描述子就可以得到mi个残差,将这mi个残差进行累加,就可以求得一个子VLAD。一个聚类中描述子贡献的子VLAD(vi)可以通过式(2)求得:

将k个vi放在一起,形成一个k×128长度的向量,即VLAD。VLAD能克服单个SIFT特征的局部限制,在更大范围表达图像的特征。
2.2 信息熵
本文利用熵[11]对SIFT描述子的空间分布信息进行统计。熵的概念被应用于众多领域,反映系统的混乱程度。在信息系统中,这种混乱程度可以用变量的概率分布来表示。
在一个系统中,假设有n个变量,变量范围标记为1~n,如果把该系统中的所有变量记为X,则X中的一个变量可标记为xi,其中i={1,2,…,n}。如果用P(xi)表示X中xi的取值概率,就可以用式(3)来计算熵值:
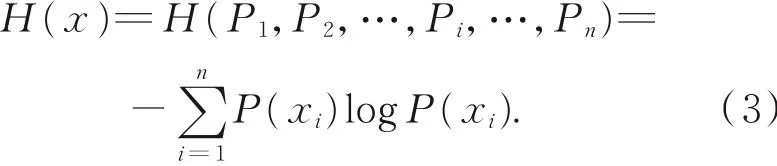
一个变量值xi按照式(3)将其概率值P(xi)与概率值P(xi)的对数值logP(xi)进行乘法计算,按照这一计算过程,将X中xi(i={1,2,…,n})的全部计算结果统一标记为H(x),就形成了该系统的熵值。
3 算法流程
本文算法利用SIFT描述子原始空间分布熵改进VLAD特征向量表达。图像中提取的SIFT特征包括向量信息和位置信息,位置信息可以用直角坐标系表达,其在直角坐标系中分布可以用熵来表达。
本文算法按照熵的计算方法对SIFT描述子的位置信息进行统计,并将产生的熵命名为空间分布熵。将空间分布熵添加到VLAD中,能够丰富VLAD特征的内容,从而达到提高VLAD特征检索能力的目的。具体计算过程如图1所示。
3.1 预处理及提取描述子
先用训练集中的全部图像训练得到k个聚类中心。然后,提取待检索图像的SIFT特征,并标注其位置信息。
3.2 分配描述子
选用最近邻算法将输入图像所有的SIFT描述子按照聚类中心进行聚类分配。依据表达SIFT描述子位置的坐标值的最大值和最小值可以确定出k个矩形区域。确定出的区域作为k个聚类中的描述子求取熵值的计算平面,计算熵值的矩形平面记为Bi,其中i={1,2,…,k}。
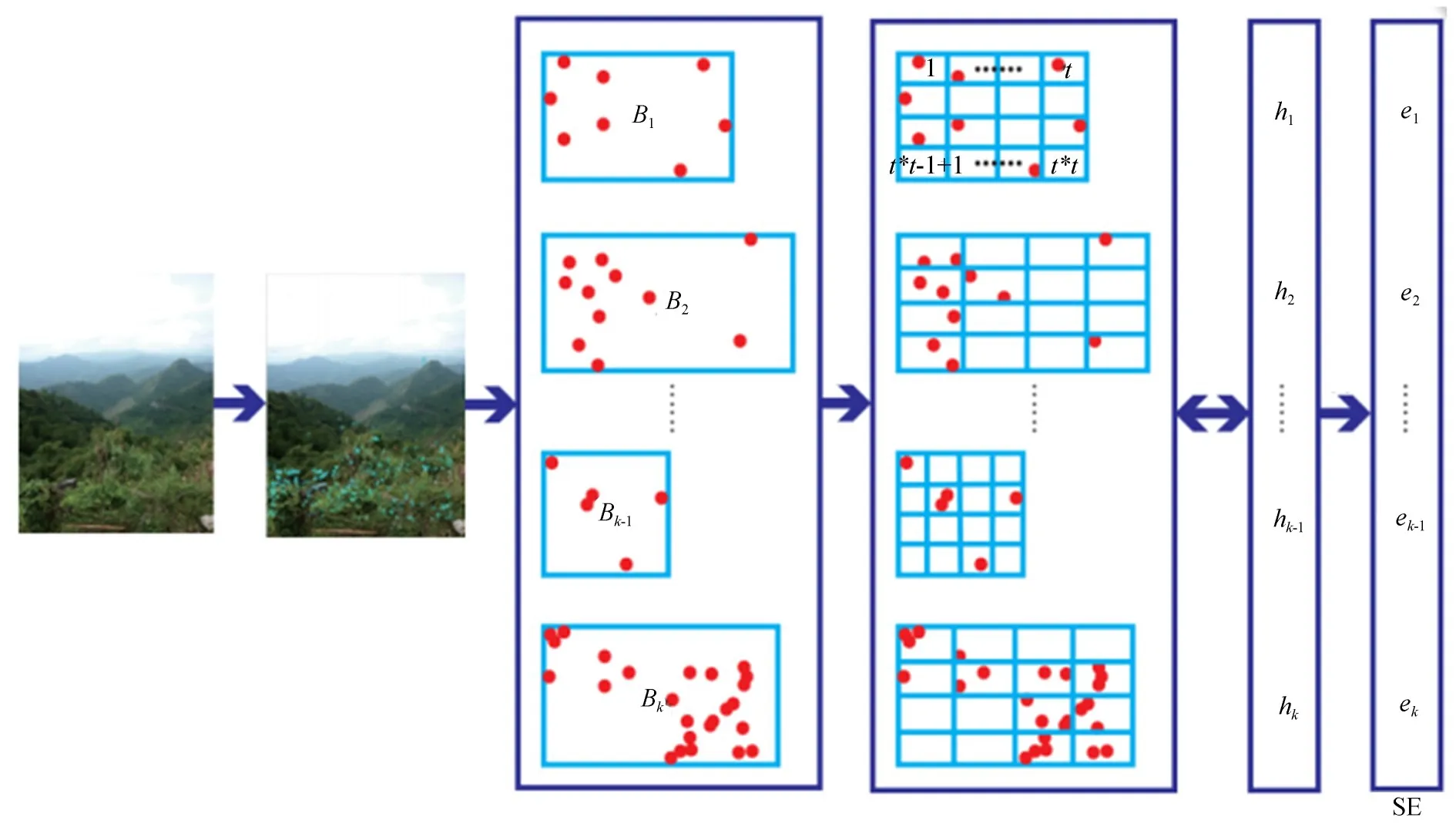
图1 改进VLAD计算模型Fig.1 Computational model of improved VLAD
3.3 计算每一子块熵值
将每一个平面分成相等的若干块,记为T块,且T=t×t。因为描述子可能是从图像中的任意像素点提取出的,所以这个描述子会以相同的概率被划分到不同的子块。如果用Pi,j表示聚类中心ci的Bi计算平面的j子块中描述子的个数,那么在这种表示中,i表示聚类中心ci的编号,其中i={1,2,…,k},k表示聚类中心的个数,j表示Bi计算平面中子块的编号,其中j={1,2,…,T},T表示一个计算平面中子块的个数。Pi,j的初始值为0。
SIFT描述子熵值的计算采用如下方法:如果描述子坐标被划分到Bi计算平面的j子块上,则聚类中心ci的Bi计算平面的j子块的描述子的个数加1。按照上述步骤确定每一个描述子所在的子块,并按照公式(4)所示,统计Bi某一子块中存在描述子的个数。

从Bi计算平面子块号1~T计算该聚类中的所有子块的Pi,j,然后对Bi计算平面这些Pi,j做归一化计算,结果记为P′i,j,之后用P′i,j来表示一个描述子划分到聚类中心ci的Bi计算平面的j子块的概率值,归一化计算过程可以通过式(5)来实现:
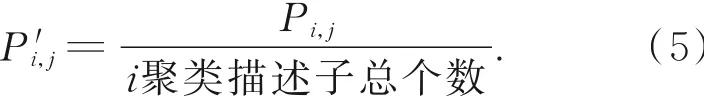
通过子块的概率值P′i,j可以计算子块的熵,计算的方法可以比照公式(3)。假设用Hi,j表示聚类中心ci的Bi计算平面的j子块的熵,则按照Hi,j=−P′i,jlog(P′i,j)可以计算其熵值,在计算过程中,如果出现P′i,j为0的情况,则log(P′i,j)也取值为0。对聚类中心ci的Bi计算平面中的所有子块(子块号j={1,2,…,T})进行Hi,j熵值计算,就会获得一个子块熵值的集合{Hi,1,Hi,2,…,Hi,j,…,Hi,T},这个熵值集合就是分布表示的该聚类的熵,记为hi。
3.4 计算空间分布熵
按照熵的概念,需要对整个体系中不同变量产生的子熵值进行累加处理,如式(6)所示,将每块求得的熵值进行累加:
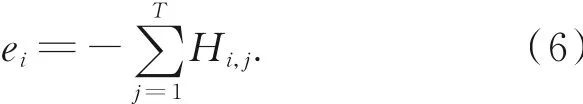
累加结果ei显示聚类中心ci的SIFT描述子位置的分布状态,表现出SIFT描述子的空间分布信息。按照这样的计算过程,每一个聚类都可以计算得到一个聚类熵值。计算全部聚类熵值后,可以获得一个k×1的熵值向量{e1,e2,…,ei,…,ek},记为SE。这个k×1的熵值向量就可以作为图像的空间分布熵。
图像的SE值是k×1的熵值向量,图像的VLAD值是k×128的特征向量,将k×128特征向量VLAD值与k×1熵值向量SE值拼接,形成了新的向量,这个新的向量是k×129的,既包含了VLAD特征信息,也包含了空间分布熵信息,本方法命名为SEVLAD。
4 实验结果
SEVLAD图像检索算法实验使用平均查准率(Mean Average Precision,mAP)指标,在IN⁃RIA Holiday[12]和Oxford5k[13]公开数据集上实现图像检索测试。
4.1 数据库介绍
Holidays公开数据集侧重风景图片,根据场景的变化分割成500组,涵盖自然风景、人工建筑等方面的高分辨率图像,在一个图像组中,待检索图像放在初始位置,随后是检索过程使用的相关图像。Holidays数据集中也包含了多组具有多种干扰的非相关图像,这些干扰包括旋转变化、角度变化、光照变化和不同程度的模糊等干扰,用于测试图像检索算法的稳定性和鲁棒性。
在Holidays公开数据集中,待检索图像和与之相关的图像涵盖了较多的场景,但对于实际需要检索的图像而言,其场景覆盖度仍然是有限的,不能保证实际检索图像涵盖与数据集内,因此在聚类中心训练时还不能依赖Holidays公开数据集提取的信息,需要补充采用Flickr60k[14]数据集中提取到的SIFT描述子进行训练。Flickr60k数据集包含了在Flickr网站上随机下载的6 000幅图片。
训练Holidays数据集聚类中心的一般方法是:利用Flickr60k数据集,在该数据集中获取SIFT描述子,利用得到的SIFT描述子训练聚类中心,将这些聚类中心用于Holidays公开数据集。
Oxford5k数据集包含有5 062幅图像,这些图像是在Flickr上对牛津大学地标性建筑搜索得到的。Oxford5k数据集对11个各异的地标性建筑依据环境状况给予标注,并且为每一个地标性建筑设置了5个用于查询的标准图像,设置了550个不同的对象。
Paris6k是一个巴黎旅游的图像数据集,共计6 412幅图像。通常的方法是利用Paris6k数据集中提取的SIFT描述子来进行聚类中心的训练。
对于Holiday和Oxford5k两个数据集,本文设定5种聚类中心对算法进行测试,具体大小为:16,32,64,128和256。现有的多种方法通常使用64或256,本算法实验采用16,32,64,128和256等5个聚类中心,通过实验数据观察聚类中心数量变化引起的检测结果的变化趋势。
4.2 图像特征归一化数据处理
作为数据处理的基本方法,在本文SEV⁃LAD算法的数据处理过程中对VLAD特征值和SE熵值采用了归一化处理方法。VLAD特征值的获取利用了SIFT描述子与聚类中心的残差向量,SE熵值的获取利用了反映位置信息的SIFT描述子划分概率累加聚类熵值,二者性质不同,各自处理。
本文SEVLAD算法实验利用空间分布熵结合多种归一化方法。在相应的归一化处理中,用VLAD来代表一般性VLAD值,用VLAD+E代表结合空间分布熵的VLAD值。在图像处理过程中,首先提取图像中一个聚类的VLAD值,并对其进行一次power归一化[15-16]。之后,依次获取图像中全部聚类的VLAD值,并对其进行一次L2归一化[17],得到的归一化结果用VLAD1表示,同时,用VLAD1+E代表结合空间分布熵的VLAD1值。这种归一化处理过程也可以采用另外一种方法,就是首先获取图像中全部聚类的VLAD值,然后统一采用power方法和L2方法进行归一化处理,按这种过程方法获取的VLAD值用VLAD2表示,用VLAD2+E代表结合空间分布熵的VLAD2值。
这里涉及到VLAD,VLAD+E,VLAD1,VLAD1+E,VLAD2及VLAD2+E 6种特征类型,按这些特征类型进行图像检索测试,并通过mAP指标评价图像检索效果。
4.3 针对Holidays数据集的实验结果
SEVLAD算法实验的检索图像来自于Holi⁃days数据集,mAP计算方法以召回1 000个图像为基准。图像检索求得的mAP值统计在表1中。表中位于同一列的数据是由不同的方法使用相同聚类中心计算出的VLAD结果。表中由左至右的聚类中心个数逐渐增多。
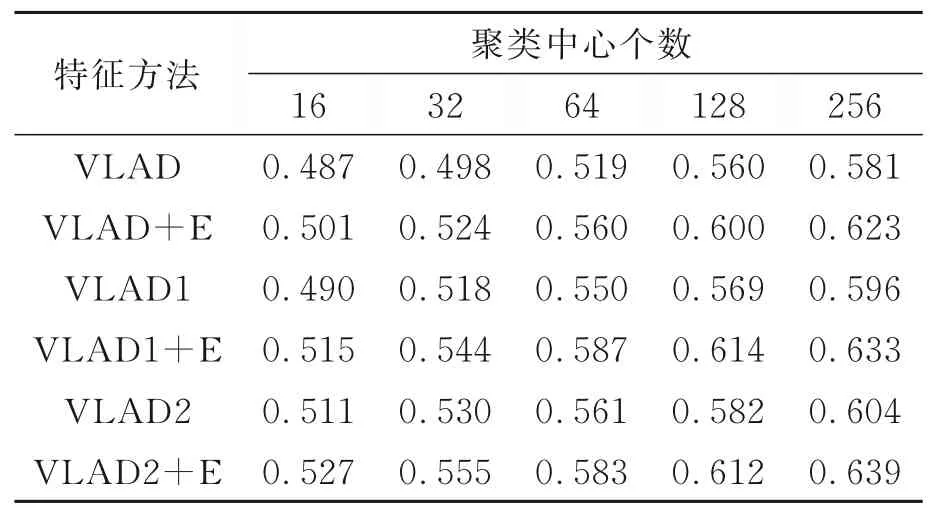
表1 基于Holidays数据集的图像检索mAP Tab.1 Image retrieval mAP on Holidays dataset
随着聚类中心个数的增加,通过SIFT描述子提取的VLAD值对图像特征的表达也更加丰富,体现在mAP指标上就是mAP值增大。具体的情况是,在VLAD一行,随着聚类中心的个数由16增加到256,mAP值也逐渐增大,而VLAD1一行相对于VLAD一行的每一列的mAP值都有增加,表现出更好的图像特征描述能力,这是因为VLAD1相对于VLAD的每一个聚类补充了power归一化处理。类似的情况也体现在VLAD2一行,包括VLAD2一行与VLAD1一行、与VLAD一行的对比。同时,由于VLAD+E、VLAD1+E和VLAD2+E分别是在VLAD、VLAD1和VLAD2基础上结合了空间分布熵,使得mAP值均有不同程度的提高,而且,实验结果也反映出VLAD2+E一行具有更好的表现力。从整体趋势上看,结合了空间分布熵的特征向量可以获得更好的检索结果。
分析SEVLAD算法在Holidays公开数据集上的实验数据,可以明显地体现出在传统VLAD方法基础上引入空间分布熵带来的变化,也就是体现在平均查准率mAP值上的变化,特别是在增加了power归一化处理过程后,这一变化显得更加突出。
4.4 针对Oxford5k数据集的实验结果
在SEVLAD算法的另一个实验中,检索图像来自于Oxford5k数据集,实验方法与在Holi⁃days公开数据集上实验的方法一样,采用SIFT描述子、SIFT描述子+归一化、SIFT描述子+空间分布熵等不同的方法完成对比实验。
SEVLAD算法针对Oxford5k数据集的图像检索mAP值统计在表2中。在表2的结构中,最上面2行表示聚类中心的个数,该实验设计了5种聚类中心,每种聚类中心包含的具体个数分别是16,32,64,128,256,表格由左至右,聚类中心个数逐次增加。通过聚类中心个数的增加,观察图像检索mAP值的变化情况。在表2结构的最左侧的一列,设计了6个栏目,表示实验采用的6个方法。与在Holidays公开数据集上实验的方法一样,使用VLAD表示采用SIFT描述子获取特征向量,使用VLAD1表示采用SIFT描述子及分步归一化方法获取特征向量,使用VLAD2表示采用SIFT描述子及统一归一化方法获取特征向量,使用+E表示结合空间分布熵获取特征向量,这样,形成的6个实验方法分别是VLAD,VLAD+E,VLAD1,VLAD1+E,VLAD2及VLAD2+E,实际上,这也是6种特征类型,是按照这些特征类型来完成图像检索实验。
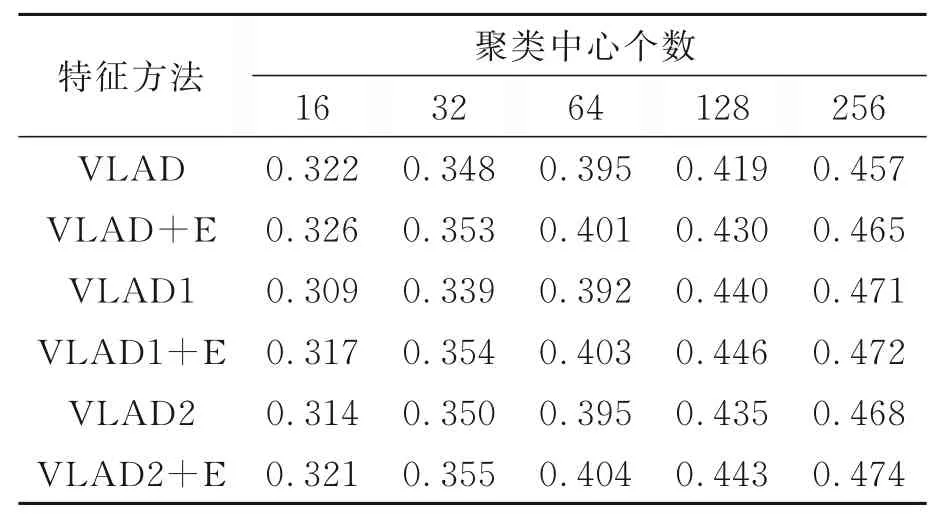
表2 基于Oxford5k数据集的图像检索mAP Tab.2 Image retrieval mAP on Oxford5k dataset
观察针对Oxford5k数据集的图像检索mAP值可以看出,对于每一行的实验结果,mAP值都跟随聚类中心数量的正向变化而呈增大趋势。mAP值越大,查准率就越高,也就意味着图像检索的结果更加准确。
不同的行,代表着不同的特征类型,实际上也代表了不同的检索方法,对比其数据,可以发现,在聚类中心的个数为16,32,64时,VLAD1的mAP值表现得不如VLAD的相应实验数据,分析其原因,VLAD1是在VLAD的基础上对一个聚类进行了归一化处理,这一处理过程导致一些特征发生变化或损失,一定程度地降低了图像描述能力。类似情况也出现在VLAD2的实验中。这些状况在聚类中心的个数为128,256时有较好的改观,说明在聚类中心个数足够多时,归一化处理带来的特征变化或损失不会影响相应方法的图像描述能力。同时,从实验数据结果中我们也可以发现,即便是在聚类中心个数较小时出现一些mAP值趋势波动,但是在融入空间分布熵后,实验数据的变化都在向增加的趋势发展。
表2 实验数据反映的情况是,SEVLAD算法使用SIFT描述子针对Oxford5k数据集的图像检索,在采用归一化处理后,特别是融入了空间分布熵后,mAP值得到增加,图像检索能力得到提升。
4.5 结合RN方法的实验结果
残差归一化(Residual Normalization,RN)方法通过预先的归一化处理来改进VLAD特征。通常利用归一化方法改进VLAD特征的途径可以从局部和全局两个角度考虑。在局部归一化方面,可以考虑在形成一个聚类VLAD值之前的过程进行归一化处理。在全局归一化方面,则一般考虑在形成一个图像VLAD值之时进行归一化处理。RN方法采用的是局部归一化思路,在形成一个聚类VLAD值之前,对残差值做L2归一化操作,规范化各个元素对VLAD值的贡献。
本文将这种方法与利用空间分布熵的方法结合,在Holiday和Oxford5k两个数据集上利用大小为64的聚类中心进行实验,得到的实验结果mAP值如表3所示。
由表可知,在本文方法的基础上结合使用RN方法能够进一步提高VLAD特征在图像检索时的查准率。

表3 添加RN方法实验结果Tab.3 Experimental results of adding RN method
5 结 论
空间分布熵的计算具有较低的空间复杂性,利用空间分布熵的VLAD与传统的VLAD相比只多出一维数据,所需的运行时间较短。在取聚类中心个数为64时,在Holidays数据集上,本文方法可将VLAD的mAP值由0.519提高到0.601,而在Oxford5k数据集上可以由0.395提高到0.408。由此可见,空间分布熵的利用能大幅度促进VLAD特征的图像检索能力。
目前,机器学习算法已经在多个领域得到应用。在图像检索应用方面,已经出现了一些利用深度卷积神经网络改进VLAD特征的方法,在此基础上,有学者设计一种新的特征表达NetV⁃LAD[18],实验数据显示,该特征并未结合其他方法就已经获得良好的效果,若进一步结合空间分布熵方法可期产生更加理想的结果。
