基于L2,1-范数距离的约束相似矩阵的聚类算法
2021-03-23马盈仓杨小飞朱恒东
张 要,马盈仓,杨小飞,朱恒东,杨 婷
(西安工程大学 理学院,陕西 西安 710600)
0 引 言
在过去的几十年中,大量的聚类方法得到了广泛的发展,并取得了令人瞩目的成就[1,2]。文献[3,4]将聚类分析的方法分为以下几类:基于密度的聚类、划分法聚类、基于网格的聚类、基于模型的聚类、层次法聚类、基于图论的聚类。
近些年来,聚类算法得到广泛的研究。学者们也发现:在聚类算法中相似度矩阵的构建是重要而基础的,对聚类结果起决定性作用[5]。所以学者们纷纷围绕如何构建更好的相似度矩阵展开研究。
经典谱聚类[6]算法使用了传统的高斯核函数来构造相似矩阵;文献[7]为消除噪声的影响,从数据自身特性出发来构造相似度矩阵,提出了一种基于自然最近邻相似图的谱聚类算法(NSG-SC);文献[8]利用欧式距离将数据集划分为若干个子集,计算其协方差,并利用设定阈值来剔除交叉点,用剔除交叉点后的新数据集来学习相似度矩阵,最后用K-Means对特征分解后的相似度矩阵进行聚类,提出了基于局部协方差矩阵的谱聚类算法。文献[9]在经典谱聚类的基础上进行改进,在无向图数据构成邻接矩阵的基础上,利用SimRank计算数据集的相似度矩阵,提出了一种基于SimRank的谱聚类算法;文献[10]提出了一种自适应模糊聚类算法(AFCM),AFCM算法中构造的观察矩阵、判断矩阵和集合划分可以自动确定合适的聚类数,为得到更好的图像分割效果,采用核距离作为相似性度量;文献[11]提出了区间模糊谱聚类图像分割方法,该方法通过区间模糊隶属度构造的区间模糊相似性测度来学习相似度矩阵,并通过规范切图谱划分准则对图像进行划分,得到最终的图像分割结果;文献[12,13]提出构建一种无参数相似图,即密度自适应邻域(DAN),它结合了距离、密度和连通性信息,反映了数据集的局部特征。
文献[14]利用距离指数变换函数和稀疏化算法构建了分块对角矩阵以重新解释样本之间的相似度;文献[15]根据核参数和共享近邻点的个数计算所有样本点之间的相似度并进行聚类。文献[16]通过改进传统谱聚类中的度量方式,用基于传递距离的度量方式度量样本间相似性;文献[17]利用密度差来调整样本点之间的相似度构造新的相似矩阵函数;文献[18]运用共享近邻来度量不同数据之间的相似程度,并利用两数据点间的主动约束信息找到他们的关系;文献[19]利用有向连接矩阵作为新的相似性度量方法;文献[20]提出一种以HowNet语义词库和BTM主题建模为基础的相似度计算方法,将两者进行线性组合,综合考察文本的相似性。文献[21]运用幂高斯核函数来求解不同数据点间的相似性,但该算法比较依赖先验信息,没有先验信息的话,就难以找到合适的参数来调节邻域尺度。
然而,许多改进后的算法仍是基于平方欧式距离来学习相似度矩阵的,如Fuzzy K-Means(FKM)[22]、CLR_W[23]、CAN[24]等。众所周知,虽然使用平方欧式距离较为方便,但却不如L2,1-范数距离更具有鲁棒性[25]。二次损失函数对异常值不具有鲁棒性。为了克服这个缺点,应该用一个对异常值不敏感的二次损失函数来代替,例如L2,1-范数。
关于算法的鲁棒性问题,CSCA算法使用了基于L2,1-范数距离的目标函数。基于“L2,1-范数”距离,它不是平方的,通常用于诱导稀疏性,与平方欧式距离相比,离群值对聚类结果带来的影响更小。考虑到用L2,1-范数距离代替平方欧式距离可以减小离群值对聚类结果带来的影响,但同时也对噪声比较不敏感。所以,本文对相似度矩阵的施加平方的约束。并且本文在优化算法上采用K邻近法来消减噪声带来的影响。最后在学习相似度矩阵的过程中,约束相似度矩阵的拉普拉斯矩阵的秩,因为这种约束,所以也能起到直接聚类的效果。并且本文对合成数据集和一些真实数据集进行了实证研究,来验证本文提出的方法。本文所希望的实验结果是——本文给出的通过约束基于L2,1-范数距离的相似度矩阵的聚类方法,在大多数情况下都优于其它相关的聚类方法。
1 新模型的建立与求解
1.1 已有模型
经典谱聚类算法[26]的基本思想是,距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,不过这仅仅是定性,而谱聚类则需要定量的权重值。所以,谱聚类利用样本点间的距离得到的相似度矩阵S来学习邻接矩阵W。关系式是使用广泛使用的自调高斯方法来构造亲和矩阵(σ的值是自调的)[26]
(1)
在学得邻接矩阵W后,经典谱聚类算法会通过解决问题(2)来进行数据处理
minTr(FTLWF)s.t.FTF=I
(2)
最后,大多数谱聚类算法[27]通过在F上运行K-Means算法,来获得最终的聚类结果。但K-Means对F要求很高,这使得聚类性能不稳定。
在文献[23]中给出了CLR_W的初始数据图的学习方法,目标函数为
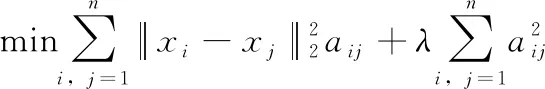
(3)
文献[28]是学习一个数据-锚点二部图(其中边的权重表示对应的数据与锚点的相似度),并基于二部图完成快速聚类的。其目标函数为
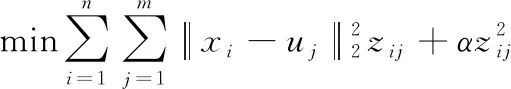
(4)
可以发现,无论谱聚类、CLR_W、CAN,还是K-Means都是基于平方欧式距离的聚类,从而会出现不够鲁棒性的问题。本文为了减小离群值对聚类结果带来的影响,采用更具有鲁棒性的L2,1-范数距离来进行初始数据图的学习。
1.2 L2,1-范数
关于矩阵的L2,1-范数在文献[29]中作为旋转不变的L1-范数首次引入,并给出了L2,1-范数的定义。L2,1-范数也被用于多标签特征选择[30]和Group Lasso[31]。
在文献[32]中指出,L2,1-范数对于行来说具有旋转不变性,其中R是任意的旋转矩阵。并将L2,1-范数推广到Lr,p-范数
(5)
式中:M∈Rn×m;mi表示矩阵M的第i行向量;mij表示矩阵M的第i行,第j列的元素。
而对于向量mi来说
(6)
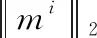
1.3 确立相似度矩阵
考虑到利用相似度矩阵的平方,来约束相似度矩阵,可以放大不同数据点间的相似度差异;同时,采用K邻近法,也可以一定程度上消减噪声对聚类结果的影响。

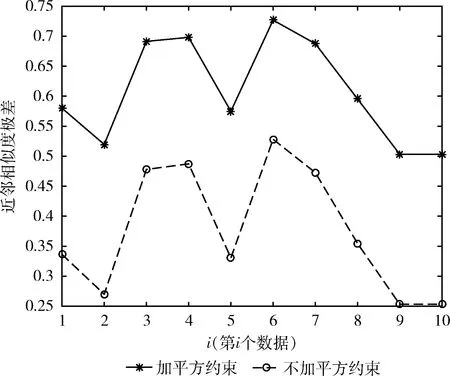
图1 是否加平方约束对相似度差异的影响
从图1中可以看出,实线始终在虚线的线上方,这说明对相似度矩阵加以平方的约束,可以放大不同数据点间相似度的差异,从而能够更好的对数据点进行聚类。
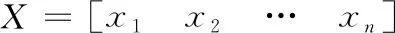
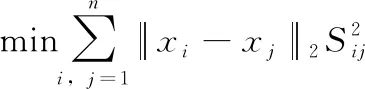
(7)
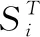
1.4 确立目标函数
由于该算法学得的相似度矩阵S是非负的,所以如果可以直接学习到恰好具有c个连接分量的结构化图,就可以不使用离散化步骤。在文献[28]指出,若相似度矩阵S是非负的,则归一化拉普拉斯矩阵LS有如定理1所示的重要性质。
定理1[28]归一化拉普拉斯矩阵LS的特征值为0的重数等于与S所对应的图中连通分量的数目。
所以,本文对学得的相似度矩阵的拉普拉斯矩阵施加约束条件:rank(LS)=n-c,从而得到聚类算法的目标函数
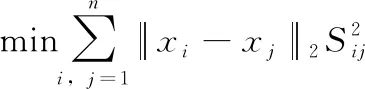
(8)
式中:LS表示S的拉普拉斯矩阵,且LS∈Rn×n。
1.5 求解目标函数
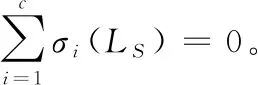
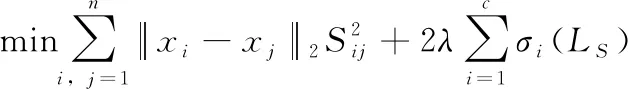
(9)
根据Ky Fan定理[33],可得
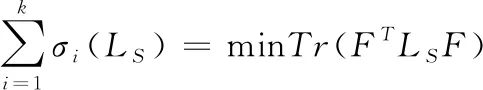
(10)
所以式(9)可以写成
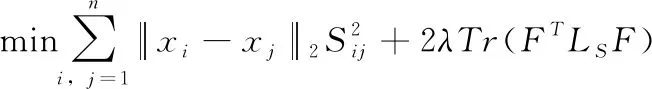
(11)
相对于式(8)而言,式(11)较容易解决。如果固定S,那么式(11)等价于
min2λTr(FTLSF)s.t.FTF=I
(12)
这里F的符合约束条件的F的最优解,就是LS矩阵的前c个最小特征值组成的特征向量。当然,在这可以用K-Means去处理F的最优解,这样也能得到聚类结果。
根据拉普拉斯矩阵的性质
(13)
式中:fi与fj分别表示F的第i行与第j行的向量。
如果F被固定,那么式(11)可以转化为
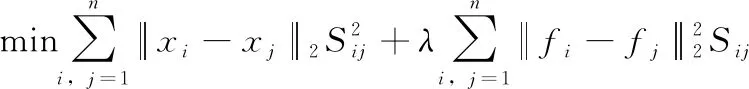
(14)
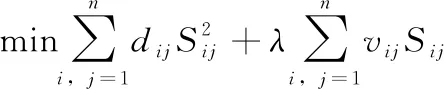
(15)
由于式(15)对于不同的i之间是相互独立的,所以对于每个i,式(15)都可以写成
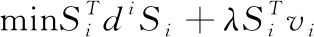
(16)
式中:vi是矩阵V的第i行向量,di是距离矩阵D的第i行向量写成的对角矩阵,即
(17)
利用拉格朗日乘子法,可以将式(16)写成
(18)
式中:α与βi均是拉格朗日因子,且有α≥0、βij≥0。
关于式(18),对Si求偏导,并令导函数的值为0,可得
(19)
对每个i而言,可以将式(19)写成
(20)
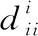
根据KKT条件[34]可知Sijβij=0,所以式(20)可以写成
(21)
从而计算出
(22)
其中
(23)
从而,可以定义函数gi(α)
(24)
gi(α)=0
(25)
因此,α的值是函数gi(α) 的根。需要注意的是,gi(α) 是一个分段线性单调递增的函数,因此用牛顿迭代法可以很容易地求出根。计算α后,由式(22)得到式(14)的最优解。
CSCA具体算法如下:
输入: 特征矩阵F,聚类数c,足够大的λ,近邻参数k。
输出: 聚类结果y。
(1)计算数据点间的距离矩阵D。
(2)初始化特征矩阵F。
(3)对距离矩阵D的每行排序。
(4)设置迭代。
for j=1,2,…,n do
定义相似度矩阵S∈Rn×n。
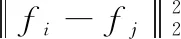
(5)更新新相似度矩阵S。
for i=1,2,…,n do
找出,第i个数据点的k近邻。
找出,k近邻所对应的vij。
对每个i,根据求解式(16)来更新相似度矩阵的Si。
end for
(6)更新特征矩阵F。

(7)设置跳出迭代条件,并用二分法调节参数λ的值。
(8)通过求图的连通分支直接得到聚类结果y。
end for
2 实验与结果
为体现本文所提出的聚类算法CSCA的可行性,选取了经典聚类算法:K-Means算法、RCut算法、NCut算法;经典子空间聚类算法:SR算法、LRR算法;以及经学者改进的算法:CLR_W算法、CAN算法,作为对比算法。并且采用准确率(Accuracy,ACC)、标准化互信(norma-lized mutual information,NMI)[35]等多种评价指标对聚类结果进行评价。
在参数方面,由于K-Means算法的不稳定性,对于 K-Means 算法、SR算法、LRR算法,采用运行10次取最大值的方法。对于RCut算法和NCut算法,实验使用了广泛使用的自调高斯方法来构造亲和矩阵(σ的值是自调的)。对于CLR_W算法与 CAN算法,实验使用了文献[23]中给出的初始数据图的学习方法,而CLR_W算法与CAN算法中的参数λ是自调的。对于CSCA算法中的参数λ与近邻参数K,其中参数λ是自调的,近邻参数K的取值为3~10。
在实验环境方面,本文所有的实验相关环境为:Microsoft Windows7系统,处理器为:Intel(R) Core(TM) i5-4210U CUP @ 1.70 GHz 2.40 GHz,内存:4.00 GB,采用编程软件为:Matlab R2016a。
2.1 人工数据集实验
在人工数据集的实验上,采用人工双月数据集进行实验。人工双月数据集是由2个集群构成的数据集,其中每个集群包含200个2维数据点为样本。双月构成的图形如图2(a)所示。噪声百分比设置为0.1。近邻参数K设置为9。实验的目标是在学习相似矩阵的同时,通过约束相似矩阵的拉普拉斯矩阵的秩,使相似矩阵中刚好有2个连通分量。用CSCA进行了测试,取得了较好的效果。在图2(a)中,数据的原始图呈现双月状,让连线的宽度表示两个对应点的亲和力。从图2(b)中可以很容易地观察到本文提出的聚类算法CSCA的有效性。
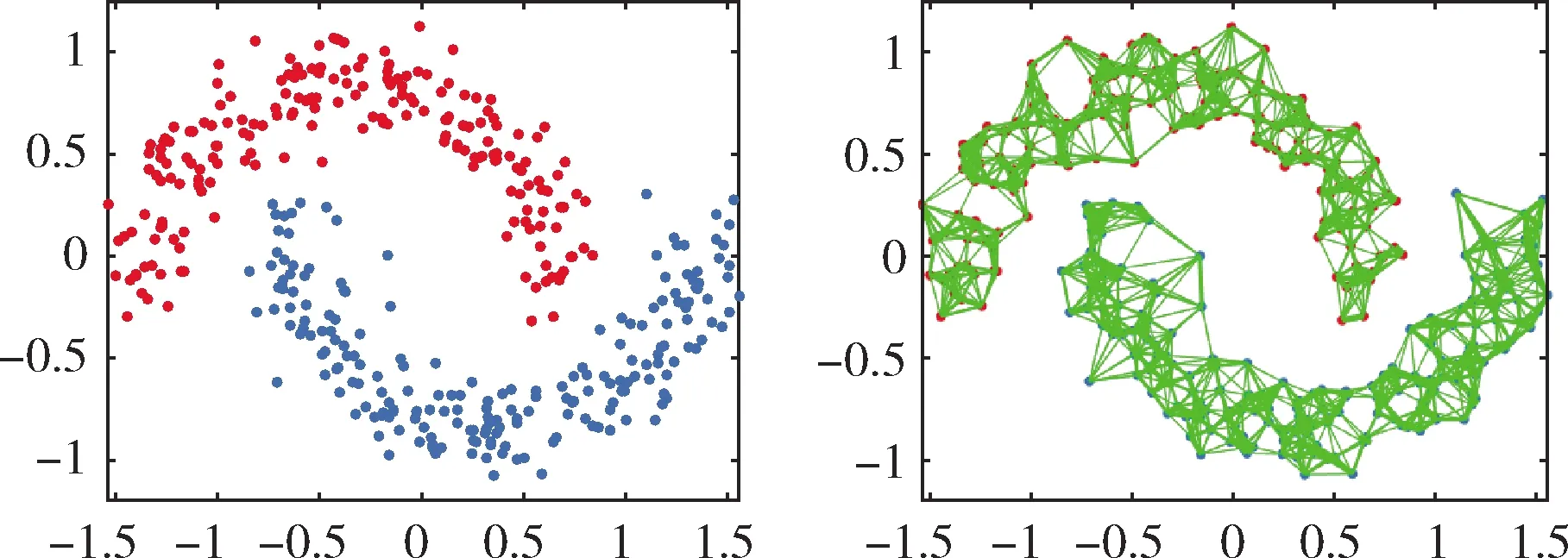
图2 双月数据原始图像与聚类结果
此外,实验还采用人工螺旋数据集Spiral进行实验。人工数据集Spiral是由3个集群构成的数据集,其中每个集群包含104个2维数据点为样本。Spiral构成的图形如图3(a) 所示。噪声百分比设置为0.1。近邻参数K设置为3~8。在图3(a)中,可以看出数据呈现螺旋状,由3条点线螺旋组成,每条线为一个集群。图3(b)则是聚类算法CSCA的聚类结果。
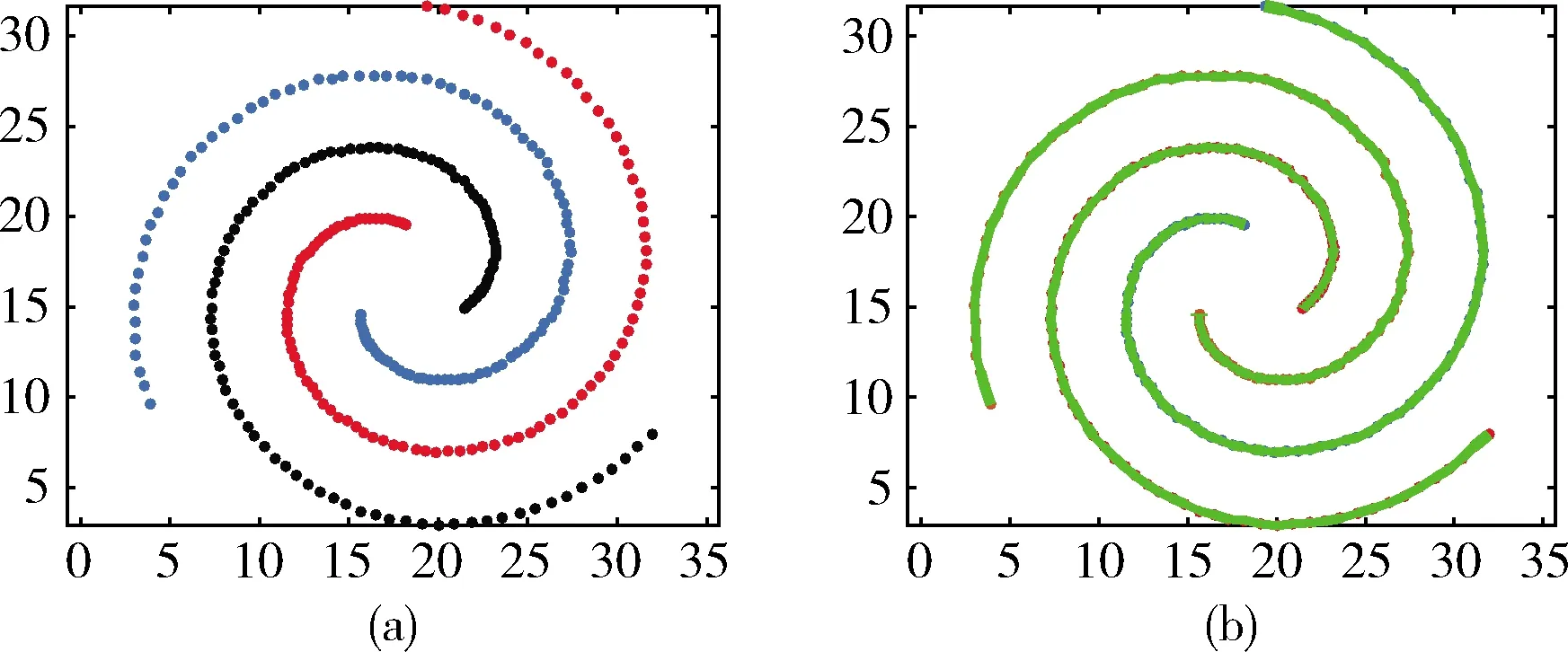
图3 Spiral原始数据与聚类结果
同时本文还分析了,在双月数据集与Spiral数据集上,近邻参数K的取值对准确率的影响。结果如图4、图5所示。从图中可以看出,近邻参数K的取值只有在一定范围时,聚类效果才能达到最好。一般为3~8。
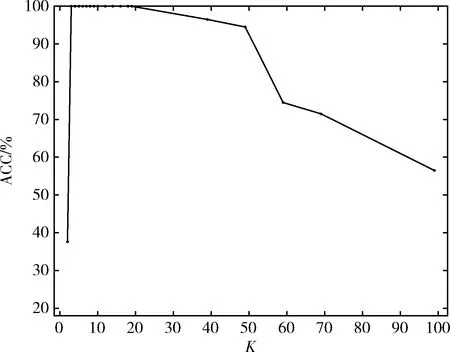
图4 CSCA算法下近邻参数K对双月数据聚类结果的影响
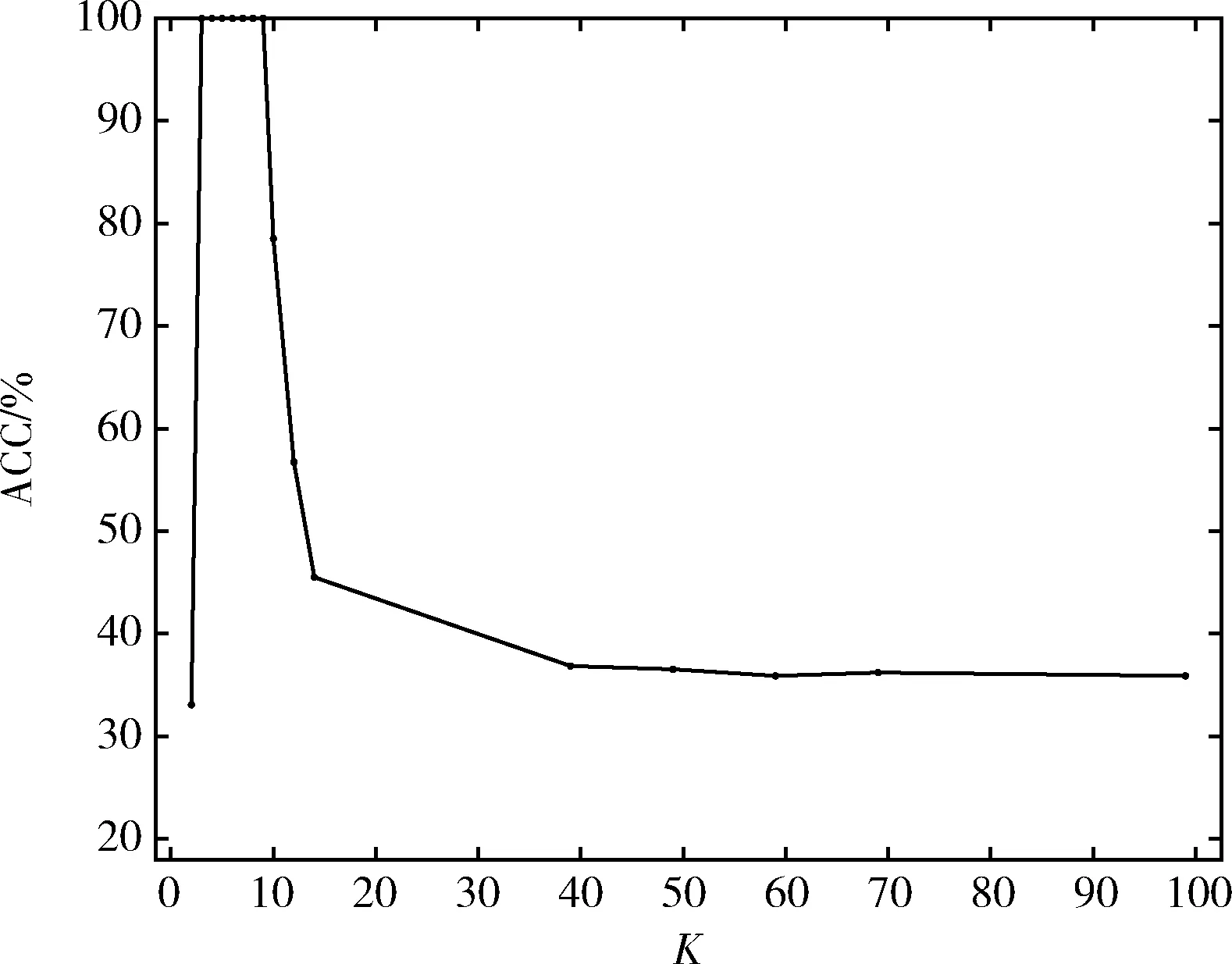
图5 CSCA算法下近邻参数K对Spiral 数据聚类结果的影响
2.2 人脸数据库(ORL)聚类
ORL包含40个不同人的面部图片,每一个都有10张不同的图片。这些照片是在不同的时间拍摄的,并改变了光线、面部表情和面部细节。所有的图片都是在暗色均匀的背景下拍摄的,支架处于直立、正面的位置(可以容忍一些侧面的运动)。每个图片的分辨率大小为92×112。
实验使用了ORL人脸数据库中的前20个人的人脸图片,共200张图片,并把每张图片转换为10 304维的数据进行实验。实验结果如图6所示,并给出CLR_W的结果,如图7所示,可以发现CSCA的实验结果明显优于CLR_W。

图6 CSCA对人脸数据集的聚类结果(ACC=88.50%)

图7 CLR_W对人脸数据集的聚类结果(ACC=77.00%)
2.3 真实数据集
在针对真实数据集的实验中,采用了6个真实数据集Yeast、Abalone、MSRA25、USPSdata20(http://www.pudn.com /Download/item/id/3945155.html)、Iris、Lung上进行实验,前两个是UCI机器学习库中的生物信息学数据集。它们含盖了高维与低维、多样本与少样本以及多类别与少类别等各种真实数据集的特点。6个真实数据集的参数见表1。
在真实数据集上的实验结果见表2、表3,其中加粗的数据表示结果最好,加下划线的次之。表2显示的是各数据集下不同算法的ACC对比;表3显示的是各数据集下不同算法的NMI对比。在真实数据集的实验结果上显示,对于不同的真实数据集,聚类算法CSCA在大多数情况下是优于其它算法的。所以,这也验证了聚类算法CSCA的有效性。
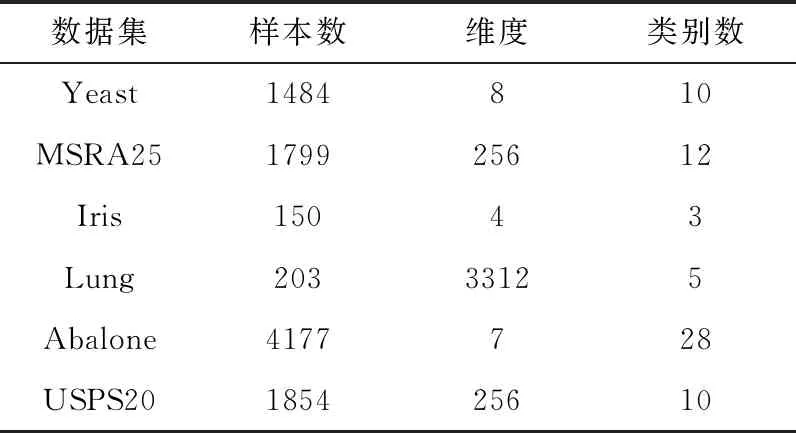
表1 真实数据集信息
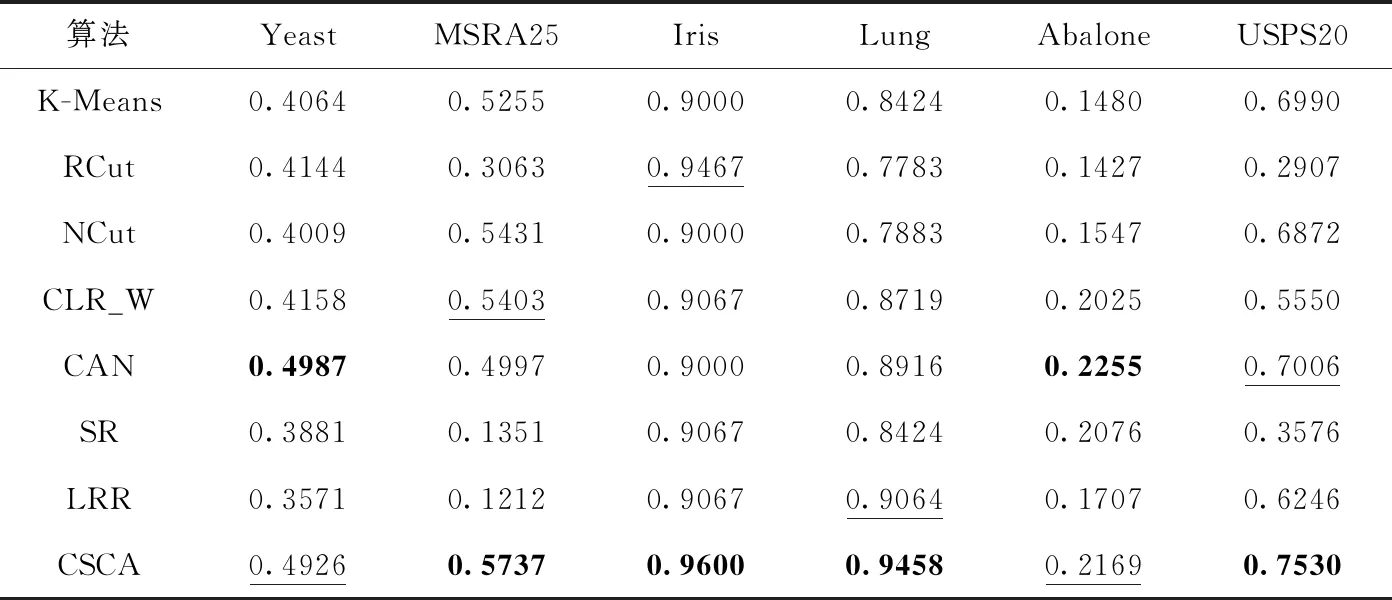
表2 各数据集下不同算法的ACC对比
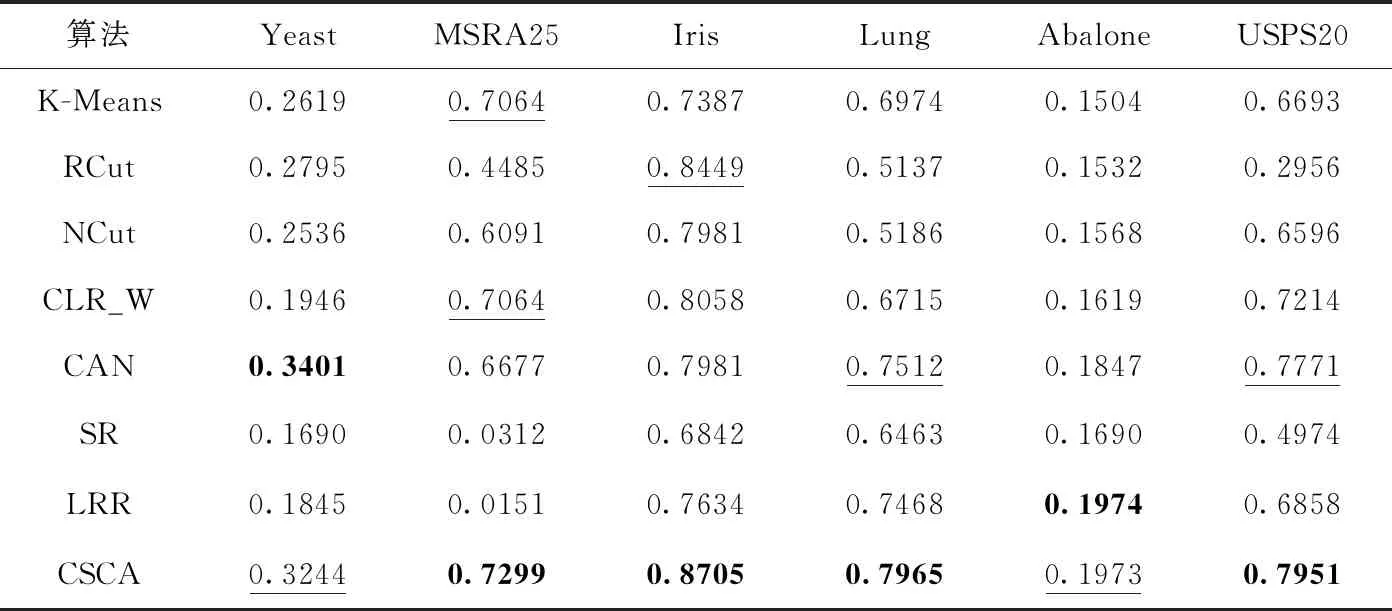
表3 各数据集下不同算法的NMI对比
3 结束语
CSCA算法是L2,1-范数距离来学习相似度矩阵的,从而增加聚类算法的鲁棒性,引导相似度矩阵的稀疏性;并用平方约束相似度矩阵;通过对相似度矩阵的拉普拉斯矩阵施加秩的约束,来实现聚类的。也可以利用K-Means对F进行聚类,得到聚类结果。该算法与对比算法相比,在大多数情况下,结果是优于对比算法的,该算法在多个数据集上的实验结果也能说明这一点。但是由于近邻参数K值的选取,是人为选取的,且对含有噪声的数据集的聚类结果影响较大。从而使得该算法具有一定的局限性,所以接下来本文将对于如何消减噪声的影响做进一步的改进。一方面,可以用其它消减噪声的影响的方法来代替K近邻,或者进一步的改进近邻参数K值的选取方法,使其在实验不同的数据集时使其能够自动调整;另一方面,可以选取合适的正则项,对相似度矩阵施加正则化,或者引入合适的半监督学习方法,来学得更好的相似度矩阵。
