求解约束优化问题的改进帝企鹅优化算法
2021-03-23李旭飞
李旭飞,王 贞
(北方民族大学 数学与信息科学学院,宁夏 银川 750021)
0 引 言
约束优化问题是工程应用[1]及科学应用中广泛研究的一类优化问题,例如:压力容器设计、焊接梁设计、机器人优化等。在解决约束优化问题时,优化算法需要高效的约束处理技术平衡约束条件和目标函数的信息。因此,研究人员设计出多种约束处理技术,常见的约束处理技术[2]有:惩罚函数法、约束和目标分离法、多目标优化法等。此外,研究人员通过对约束处理技术进行改进[3]或对约束处理技术进行混合来设计更好的约束处理技术求解约束优化问题。另一方面,研究人员在设计有效的约束处理技术基础上,也通过改进搜索算法来提高约束优化算法的性能。近些年,研究者们在求解约束优化问题的智能算法研究上有大量的成果。Long等针对萤火虫算法收敛速度慢、易早熟等缺点,提出一种改进萤火虫算法求解约束优化问题。Liu等[4]在教与学优化算法中引入自我学习过程,从而提出协同进化教与学优化算法求解约束优化问题。Wang等[5]提出了一种自适应的人工蜂群算法求解约束优化问题等。
帝企鹅优化算法[6](emperor penguin optimizer,EPO)是Gaurav等提出的一种新型群智能优化算法,其思想是模拟帝企鹅群体冬天拥挤在一起取暖的行为进行寻优。Baliarsingh等[7]进一步将EPO算法用于求解多目标优化问题。Kumar等[8]将EPO算法用于处理图像分割问题。Jia等[9]通过结合多项式变异、levy飞行及热交换操作策略改进帝企鹅优化算法。尽管,EPO算法的研究已取得部分研究成果,但算法仍存在迭代后期收敛速度慢、易陷入局部最优等缺点。因此,本文提出了改进帝企鹅优化算法(improved emperor penguin optimizer,IEPO)用于求解约束优化问题。IEPO算法利用动态线性调整粒子数目策略结合两种变异操作的替换使用,平衡了算法的全局探索能力与局部开采能力,从而提高算法的收敛速度。算法通过存档替换机制完善了可行性准则性能,增加了算法的收敛精度,提高了算法跳出局部最优的能力。最后,将IEPO算法用于求解13个标准约束优化测试函数验证算法的有效性,并应用到2个实际工程问题中检验算法性能。
1 基本帝企鹅优化算法
EPO算法是模拟帝企鹅群体冬季取暖的群智能优化算法。该算法利用群体中心温度最高点的个体为最优个体引导其它个体向最优点移动,从而达到寻优目的。种群中个体位置由最优个体引导移动,具体如下所示
(1)
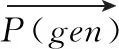
(2)
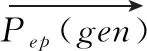
(3)
式中:f和l两个参数分别代表算法迭代过程中探索与开发,它们的取值范围分别为[2,3],[1.5,2]。
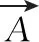
(4)
(5)
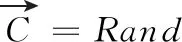
(6)
其中,T1是帝企鹅群体的温度变化函数;M=2是避免帝企鹅个体间碰撞的一个控制参数;Pgrid(Accuracy) 是最优个体到其它个体位置的绝对值;Rand是[0,1]上均匀分布的随机数。T1的具体表达式如下

(7)
(8)
其中:maxGen是算法最大迭代次数;R表示企鹅群体围成多边形区域的半径;T代表在搜索空间中寻找最优解的时间。
基本EPO算法步骤如下。
算法1:帝企鹅优化算法
(1)设置算法参数并初始化。种群数量Popsize,最大迭代次数为maxGen,当前代数为gen,在解空间中随机初始个体位置;
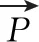
(3)利用式(7)、式(8)先确定群体范围的温度变化趋势;
(4)根据式(1)、式(2)、式(4)更新群体的当前位置;
(6)判断算法是否满足终止条件,若满足,则输出最优值;否则,转(3)。
2 改进帝企鹅优化算法
EPO算法缺少变异机制,导致算法在搜索后期收敛速度慢,易陷入局部最优。因此,IEPO算法通过引入两种变异操作机制结合动态线性调整粒子数目策略,在迭代前期可以增加算法的全局搜索能力,后期提高算法的局部勘探能力。为了平衡约束条件和目标函数信息,在可行性准则中加入存档替换操作机制,并在IEPO算法中使用目标函数最优值个体作为最优引导个体。
2.1 变异策略
差分进化算法是一种随机搜索的进化算法,该算法具有很好的全局搜索能力和局部探索能力。在变异操作中,DE/current-to-rand具有较好的探索能力,可以增加算法的全局搜索能力;DE/current-to-best具有很好的开发能力,可以增加算法的局部搜索能力,使算法能够快速找到最优解[10]。因此本文利用上述两个变异操作来增加算法的寻优能力。具体如下所示:
DE/current-to-best/1
Vi,gen+1=xi,gen+rand·(xbest,gen-xi,gen)+F·(xr1,gen-xr2,gen)
(9)
DE/current-to-rand/1
Vi,gen+1=xi,gen+rand·(xr1,gen-xi,gen)+F·(xr2,gen-xr3,gen)
(10)
其中,随机选择的序号r1、r2和r3互不相同,且与目标向量序号i也不相同;xr1、xr2和xr3是种群中随机选取的个体;Vi是个体xi的变异个体;xbest是当前种群最优个体;变异算子F∈[0,2],是一个实常数,控制偏差变量的放大作用;rand是[0,1]上均匀分布的随机数。
为保证IEPO算法的搜索性能,本文利用动态线性调整粒子数目策略[11]结合式(9)和式(10)不同的变异操作进行变异。将种群分为两个子种群N1和N2,对应子种群数量分别为Popsize1和Popsize2。 在算法早期搜索时,子种群N1使用DE/current-to-rand进行变异操作增加种群多样性,让更多的个体参与到全局搜索过程中。随着算法迭代到后期,为保证局部搜索能力,子种群N2使用DE/current-to-best来提高算法的局部探索能力。既可以平衡算法收敛速度与种群多样性,又使得种群能快速进入可行域并收敛到最优点避免陷入局部最优。动态线性调整粒子数目策略具体计算方式如下
Popsize1+Popsize2=Popsize
(11)
Popsize2=floor[(gen/maxGen)·Popsize]
(12)
算法2: 变异操作
(1)fori=1∶Popsize
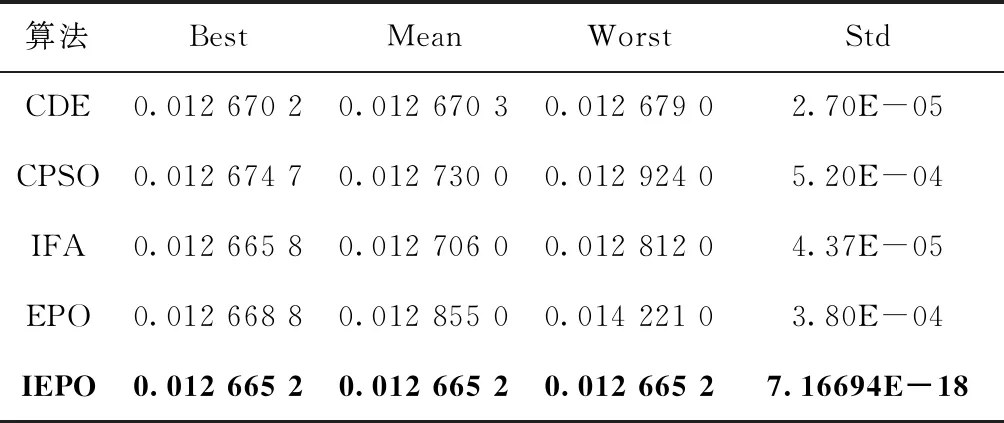
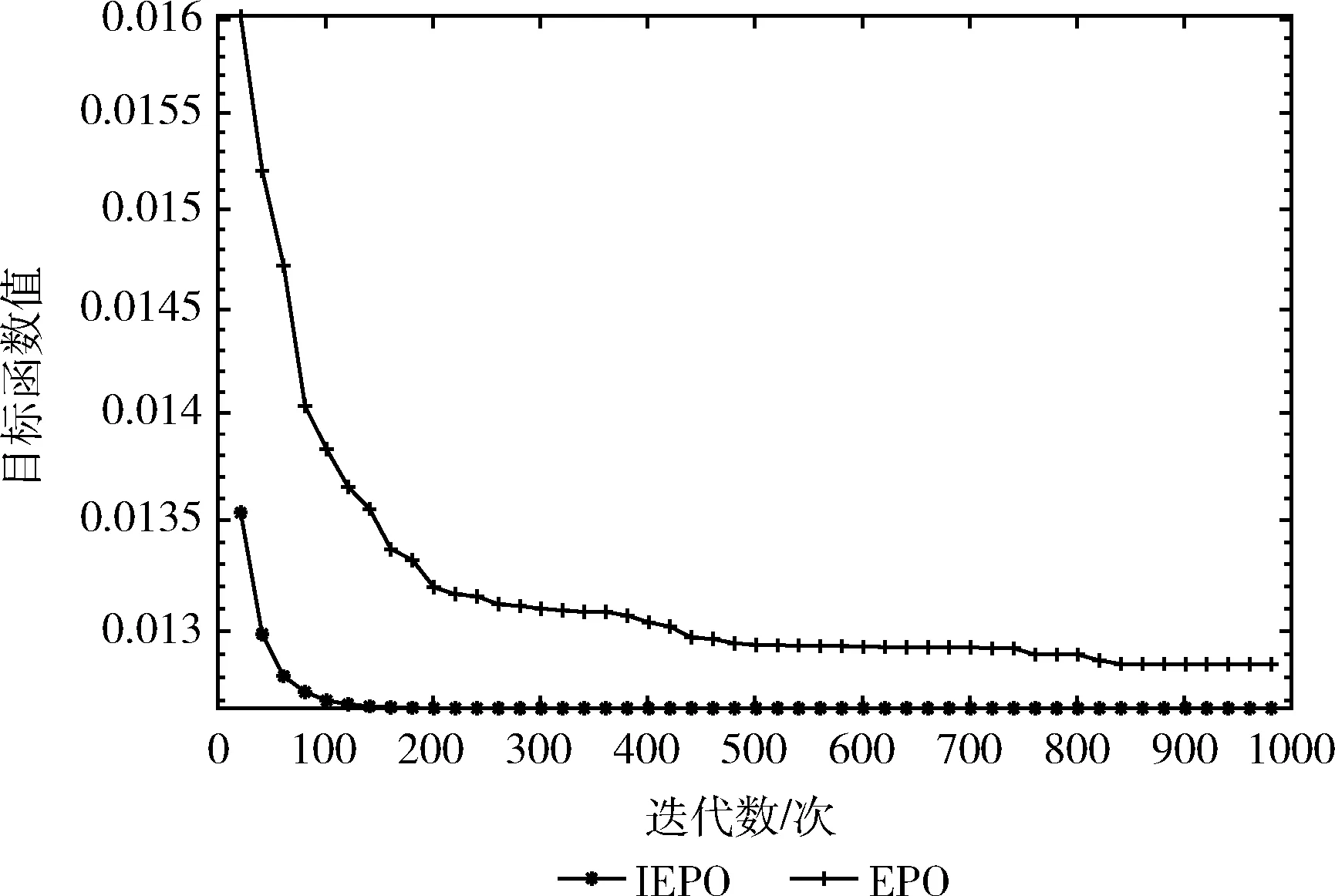
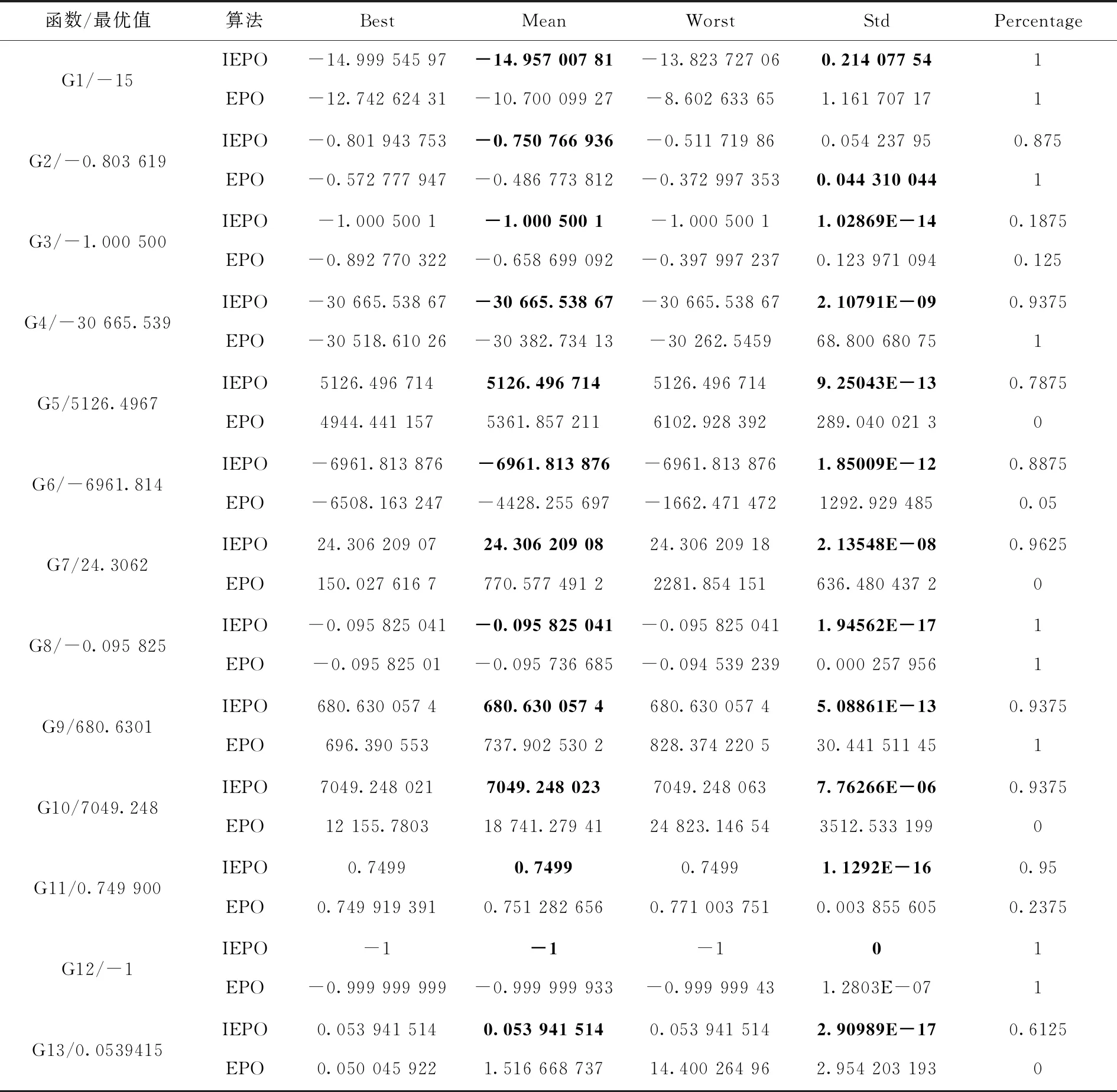
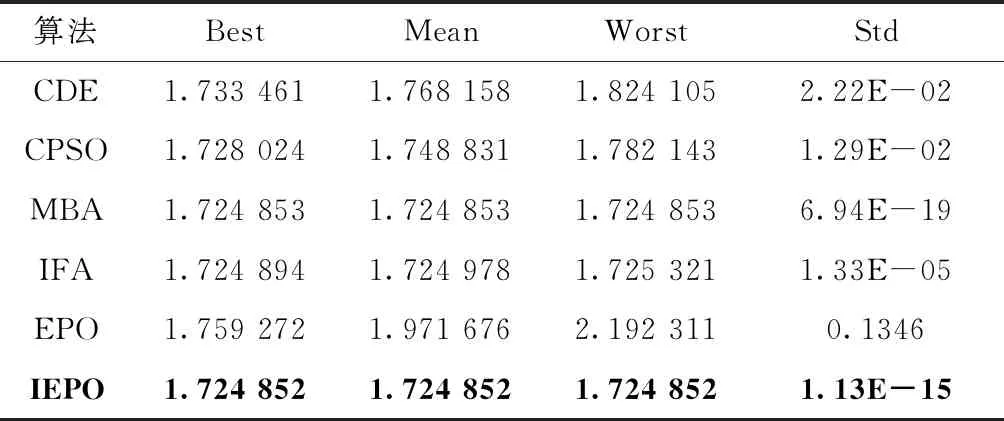
(2)ifi (3) 利用式(9)进行变异操作; (4)else (5) 利用式(10)进行变异操作; (6)end (7)end 可行性准则在处理约束问题时简单有效,因此是常见的一种约束处理技术。它通常采用以下3条准则比较两个个体的优劣。 (1)可行个体与不可行个体比较,选择可行个体; (2)两个可行个体比较,选择目标函数值好的个体; (3)两个不可行个体比较,选择约束程度小的个体。 在第一种情况中,如果不可行个体相比可行个体距最优点更近,此时如果能够选择保留不可行个体则可能使算法更快收敛于最优点。可行性准则过度偏好于约束条件的信息,没有充分利用具有较好目标函数值的个体。鉴于上述情况,文献[12]使用了一种存档替换机制,在算法中存档约束程度小且目标函数值占优的个体,然后通过替换种群中目标函数值较劣的个体,使算法充分平衡约束条件和目标函数的信息。具体的存档替换机制如下: 算法3: 存档替换机制 (1)将种群按目标函数值降序排列,平均分为m个子种群; (2)令i=1; (3)While|A|>0andi (4) 从等分群体的第一个部分中选取约束程度大的个体记为xa; (5) 从存档A中选取约束违反程度小的个体记为xb; (6)Iff(xb) (7) 用xb替换xa,并从种群中删掉xa; (8)endIf (9)i=i+1; (10)endWhile IEPO算法具体步骤如下。 算法4:改进帝企鹅优化算法 (1)设置算法参数并初始化。种群数量Popsize,最大迭代次数为maxGen,当前代数为gen=1,在解空间随机初始种群个体位置; (2)计算每个个体目标函数值和约束违背程度; (3)利用式(7)、式(8)先确定群体范围的温度变化趋势; (4)根据式(1)、式(2)、式(4)更新群体的当前位置; (5)利用可行性准则比较父代与子代个体,并保留优秀个体; (6)利用算法2变异操作,提高算法搜索能力; (7)利用算法3选择优秀个体作为下一代进化个体; (8)判断算法是否满足终止条件,若满足,则输出最优值;否则,转(3)。 通过算法1与算法4相比较可知,在EPO算法中引入变异操作,可以使算法在整个寻优过程中灵活搜索,增加种群多样性,有效避免算法陷入局部最优。改进可行性准则策略的引入,能使算法保留较优不可行个体,当保留个体比当前种群中的个体更快接近最优点时,通过保留个体替换当前种群中目标函数值较劣的个体,使得算法跳出局部最优。改进可行性准则充分利用约束条件和目标函数信息,提高了算法的寻优能力。变异操作和改进可行性准则策略的结合,克服了帝企鹅优化算法求解约束优化问题时收敛精度低、易陷入局部最优等问题。 根据算法1可知EPO算法的时间复杂度为O(maxGen×Popsize×n),其中:maxGen为最大循环次数,Popsize为种群数量,问题维数为n。 IEPO算法相比于EPO算法,将种群随机初始化时间复杂度为O(Popsize×n)。 IEPO算法在每次迭代过程中增加了变异操作,则其时间复杂度为O(maxGen×Popsize×n)。 所以IEPO算法的时间复杂度为O(Popsize×n+maxGen×Popsize×n),即:O(maxGen×Popsize×n)。 所以IEPO算法的时间复杂度为O(maxGen×Popsize×n)。 为了验证改进帝企鹅优化算法(IEPO)对约束优化问题的有效性,本次实验采用13个标准约束优化测试函数进行实验比较。具体的测试函数情况参考文献[13]。在实验中,设备处理器为:inter(R) Core(TM) i7-6500U CPU@2.50 GHz 2.59 GHz,内存4 G。算法均在MATLAB2014a中进行实验。 本次实验将IEPO算法与EPO算法进行比较。参数设置如下:种群数量均为80,最大迭代次数为1000次,对算法均进行30次独立实验。 实验结果见表1,分别给出IEPO算法和EPO算法的实验结果对比,Best、Mean、Worst和Std分别是算法独立运行30次的最优值、平均值、最差值和标准差,标准差反映了算法的稳定程度,Percentage表示可行解所占种群的比例。可以看出在测试优化问题中,IEPO算法都优于EPO算法,且能寻找到所有优化问题的可行解;并且在G3、G4、G5、G6、G7、G8、G9、G10、G11、G12、G13这些问题中,IEPO 算法可以比较准确寻找到函数最优值,G12有非常好的稳定性,在剩余优化问题上算法也表现出良好的稳定性。在G1、G2等问题中IEPO也没有寻找到函数最优值。 结合表1中的数据和图1中收敛曲线,可以推断出 IEPO 算法通过上述改进的策略可以有效避免在寻找到最优点之前出现早熟现象,而EPO算法不仅在可行域外出现停滞现象,在可行域内也出现陷入局部最优的情况。 表1 EPO算法与IEPO算法对约束优化问题寻优对比结果 图1 EPO算法与IEPO算法部分约束优化问题收敛曲线对比 为了进一步验证IEPO算法在约束优化问题上的性能,接下来与文献[13]中ABC、PSO及HCS-LSAL和文献[14]中ICA等算法的优化结果进行比较,并且算法参数设置与原参考文献中相同,比较结果见表2。其中Na表示原文中没有相对应数值,表中加粗表示较好结果。可以看出,在函数G3、G5、G7、G9、G10、G11、G12、G13上,IEPO 不仅可以寻找到最优值,而且稳定性更好;在函数G4、G6、G8上,IEPO算法能寻找到最优值,但标准差比其它算法大,稳定性较弱;在问题G1、G2上,IEPO算法没有寻找到函数最优值,但平均值非常接近最优值;从而可以得到,IEPO算法在约束优化问题上有很好的寻优效果。 表2 不同算法对约束优化问题寻优对比结果 表2(续) 为验证IEPO算法对现实工程问题优化的性能,将该算法应用于焊接梁设计和拉力/压力弹簧设计这两个工程问题上。将EPO和IEPO算法分别独立运行30次,算法其它参数设置见3.1节。 焊接梁优化设计的主要目标是在一定约束条件下使其费用最小,该问题的4个决策变量分别为h(x1)、l(x2)、t(x3)、b(x4),问题的具体表达形式如下 其中 P=6000;L=14;E=30×106;G=12×106;τmax=13600;σmax=30000;δmax=0.25; 0.1≤x1≤2.0; 0.1≤x2≤10.0; 0.1≤x3≤10.0; 0.1≤x4≤2.0。 通过IEPO算法求解焊接梁结构设计优化问题,并与EPO算法以及文献[1]中CDE、CPSO、MBA、IFA等算法结果比较见表3,表中加粗表示较好结果。从表3中可知,在焊接梁结构优化设计上IEPO算法明显优于EPO算法;平均值和标准差都优于CDE、CPSO、IFA等算法;与MBA算法相比,平均值略优;图2为EPO算法与IEPO算法在焊接梁结构设计优化上的收敛曲线,可以直观看出,IEPO算法的收敛精度和速度都优于EPO算法。 拉力/压力弹簧优化设计的主要目标是在一定约束条件下最小化张力弦质量,该问题的数学具体表达式如下 其中,0.25≤x1≤1.30; 0.05≤x2≤2.00; 2.00≤x3≤15.00。 表3 不同算法对焊接梁问题优化结果对比 图2 焊接梁结构设计问题优化收敛曲线 利用IEPO算法求解拉力/压力弹簧结构设计问题,并与EPO以及文献[1]中CDE、CPSO、IFA等算法进行比较,比较数据见表4,表中加粗表示较好结果。从表4中可知,IEPO算法在拉力/压力弹簧结构设计等优化问题上优于EPO算法,平均值和标准差都优于CDE、CPSO、IFA等算法。图3为EPO算法与IEPO算法拉力/压力弹簧结构设计的收敛曲线,可以直观看出,IEPO算法的收敛精度和速度更优。 针对约束优化问题,本文提出一种改进帝企鹅优化算法。通过标准的测试优化函数及实际工程问题验证,IEPO算法利用两种变异操作可以充分平衡全局搜索和局部开采能力。动态线性调整粒子数目策略,可以有效增加算法的收敛能力。此外,增加存档替换机制的可行性准则可使得算法有效避免了早熟现象。通过实验结果验证本文提出的改进帝企鹅优化算法可以有效解决约束优化问题。 表4 不同算法对拉压弹簧设计问题优化结果对比 图3 拉力/压力弹簧结构设计问题优化收敛曲线2.2 改进可行性准则
2.3 IEPO算法步骤
2.4 算法时间复杂度分析
3 数值实验及分析
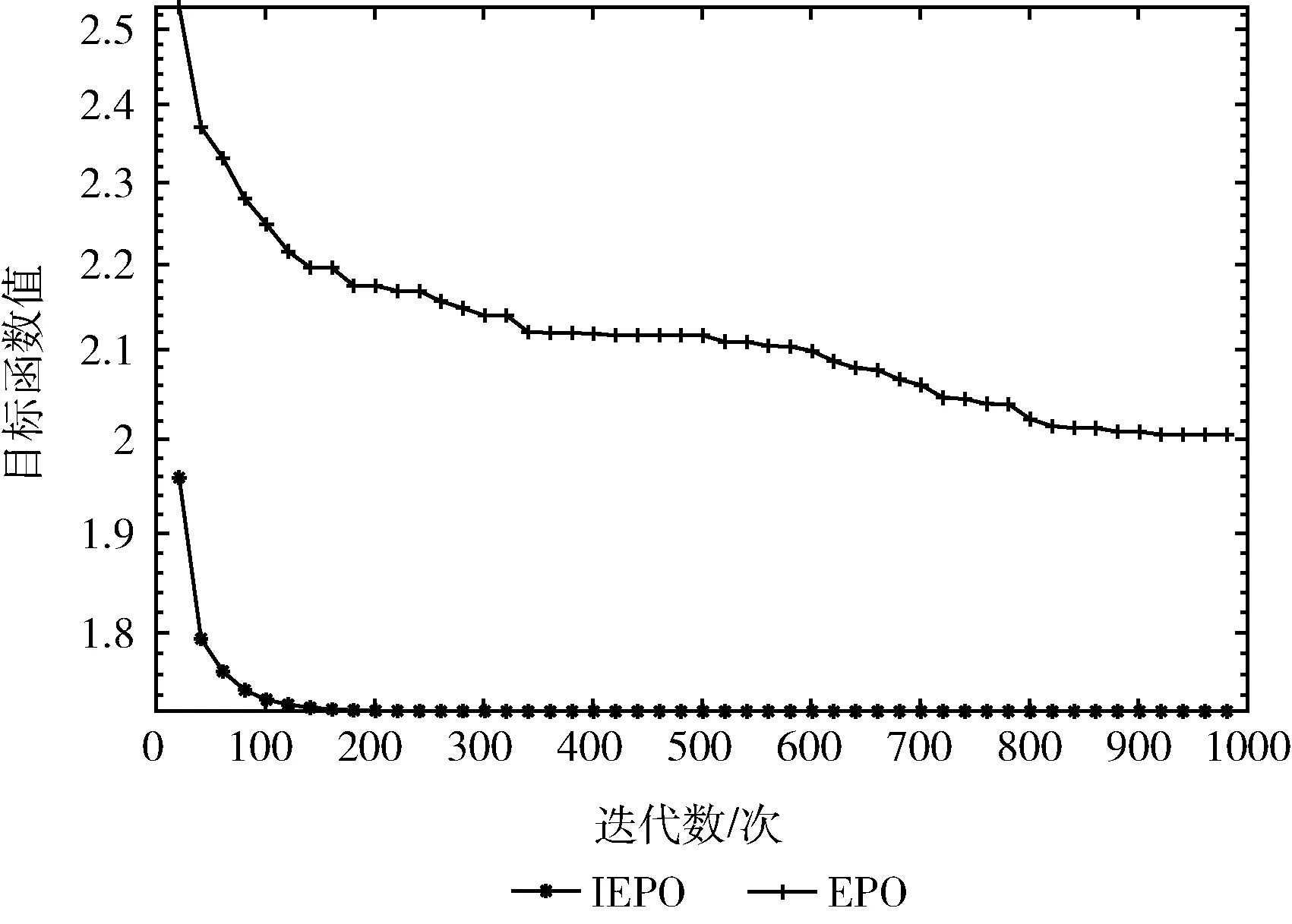
3.1 与原始帝企鹅优化算法比较
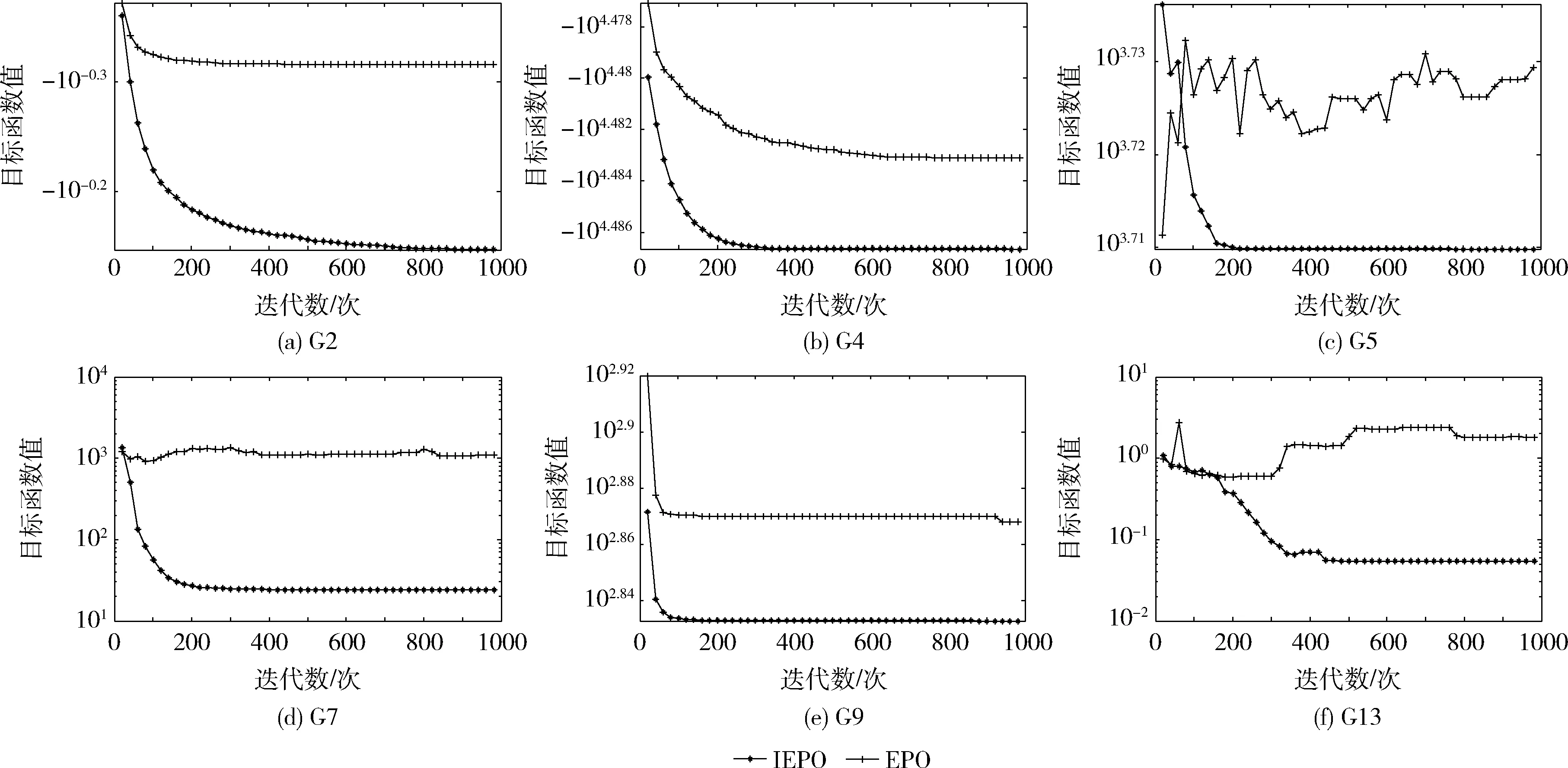
3.2 IEPO与其它优化算法的比较
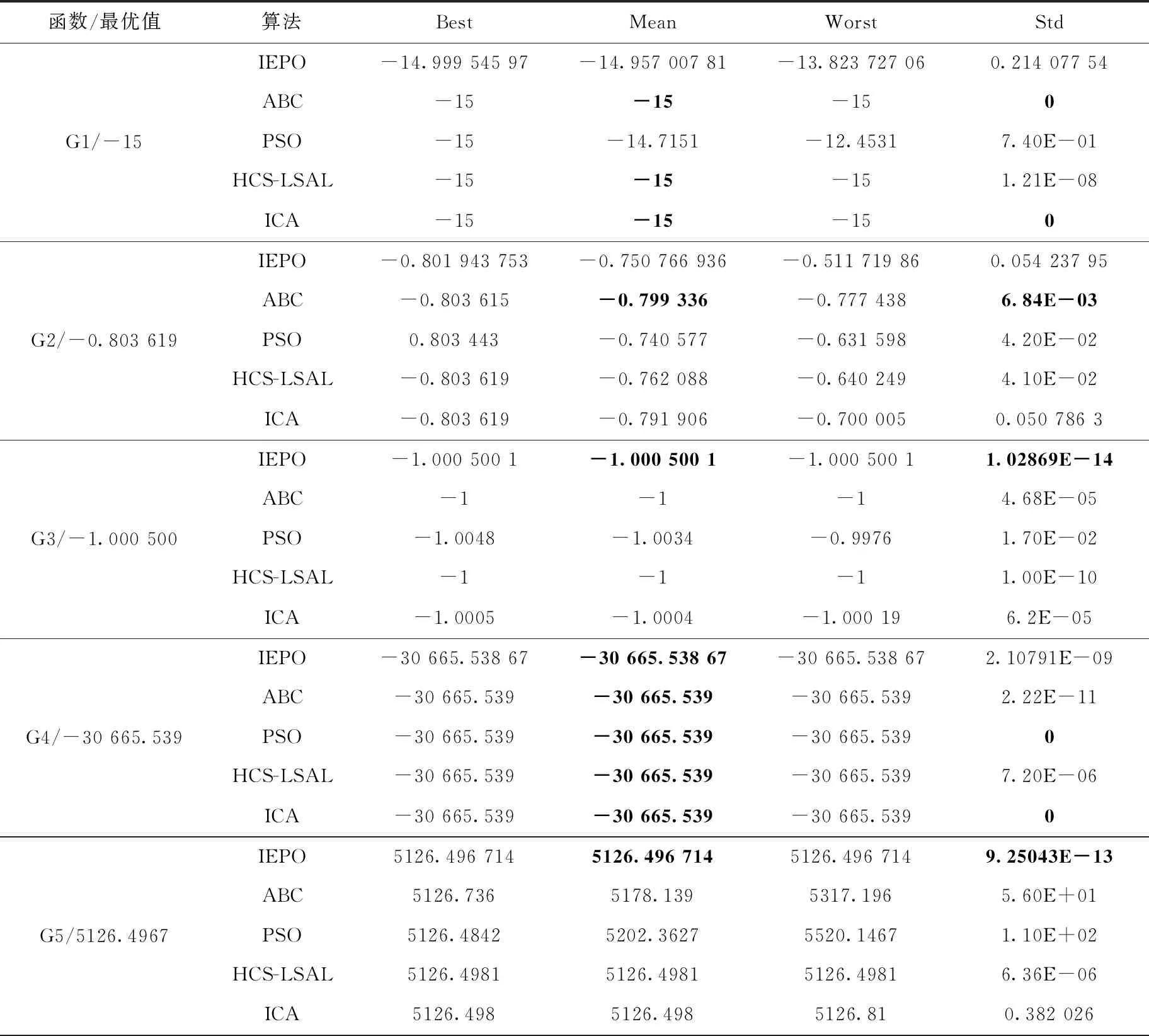
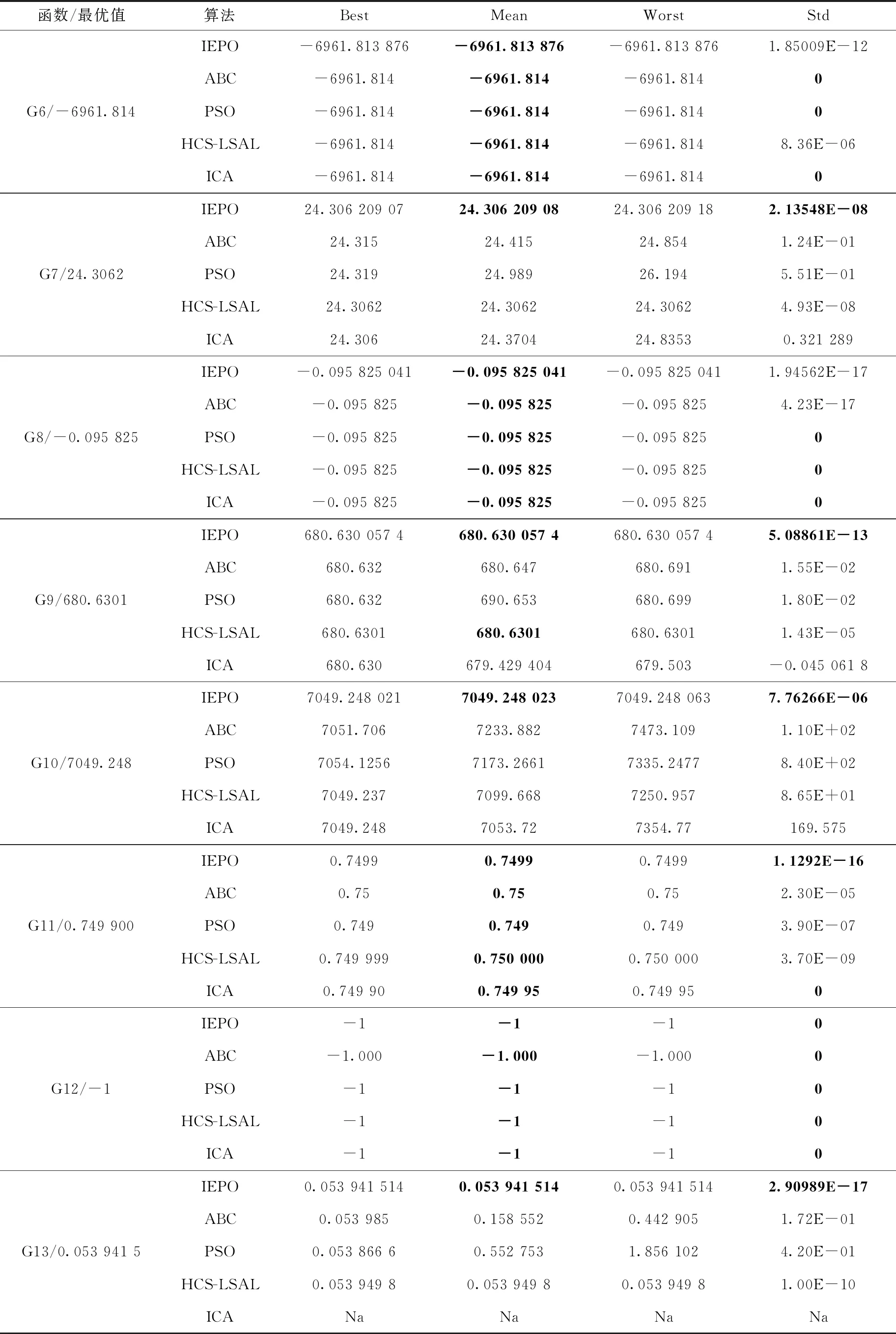
4 工程优化中的应用
4.1 焊接梁设计问题
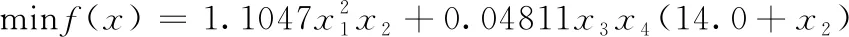
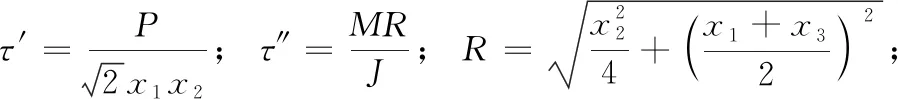
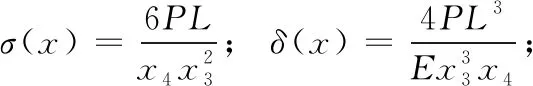
4.2 拉力/压力弹簧设计问题
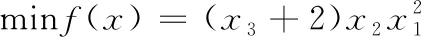
5 结束语