PLC中联合PTS的脉冲噪声抑制技术
2021-03-23王俊杰龙江航莫雪莎
管 春,王俊杰,龙江航,莫雪莎
(重庆邮电大学 光电工程学院,重庆 400065)
0 引 言
大多数电力线通信(power line communication,PLC)系统采用多输入多输出(multiple-input multiple-output,MIMO)技术,采取三线传输信息,以提高通信效率和覆盖率。然而由于多输入输出信号和脉冲噪声会引起自干扰,且当功率超过特定值时,这种干扰会对MIMO-PLC系统造成很大影响,导致系统的信噪比降低,误码率(symbol error rate,SER)提高[1]。目前,因为方法简单且易于实现,非线性法成为实际中抑制脉冲噪声应用最广泛的方法。根据前人的研究,主要的非线性法有3种,分别是置零法(Blanking)、限幅法(Clipping)和混合法(Blanking-Clipping)。Blanking技术最为简单,能够有效减少脉冲噪声干扰[1]。其理论是,当接收信号的功率大于预设阈值时,将信号置为0。Blanking-Clipping技术易于实现,提高了系统性能,在基于正交频分复用技术(orthogonal frequency division multiplexing,OFDM)的PLC系统中得到了广泛的应用[2]。研究表明,在信号脉冲噪声之比(signal to impulsive noise rate,SINR)较低时,Blanking技术性能优于Clipping;在SINR较高时,Clipping技术性能优于Blanking;Blanking-Clipping技术在SINR高低情况下性能都优于前两者。对于基于OFDM的PLC系统这种典型的多载波系统,信号通常存在高峰均比(peak to average power ratio,PAPR)的情况,这会影响Blanking-Clipping技术的降噪性能。其原因有,首先,传输信号的PAPR过高通常伴随有其接收功率往往大于设定的阈值,从而在置零时和限幅时将传输信号误视为噪声;其次,信号的PAPR过高会导致不能完全识别脉冲噪声,致使部分脉冲噪声被忽略。
由此,针对具有大量脉冲噪声干扰的PLC系统,本文提出了联合部分传输序列(partial transmission sequences,PTS)的Blanking-Clipping技术。首先,由于信号高PAPR引起的降噪性能降低,本文通过在发射端引入PTS技术降低信号的PAPR以便于后续处理;而后,在接收端再对信号置零和限幅。仿真结果表明,与其它非线性技术相比,该技术有着更好的降噪性能。
1 系统模型
1.1 MIMO-PLC模型
MIMO-PLC系统如图1所示,根据文献[3]的工作,将PLC系统结合其三线传输的特征,建立电力线的MIMO信道模型,其中,三线分别为相线(phase,P)、零线(neutral,N)、接地保护线(protective earth,PE)。
根据电力线耦合原理,信号通过两线之间的电压差来传输,有3个发射端口,即P到N,P到PE,N到PE[4]。

图1 MIMO-PLC信道模型
图2中是有M个发射端口和N个接收端口的MIMO-PLC系统,PTS模块用于降低信号的PAPR,sn为采用QAM调制的输入信号,xm为PTS处理后第M个发射端口的输入信号,yn为经过电力线信道后第N个端口的接收信号,s′n为解调后的输出信号。
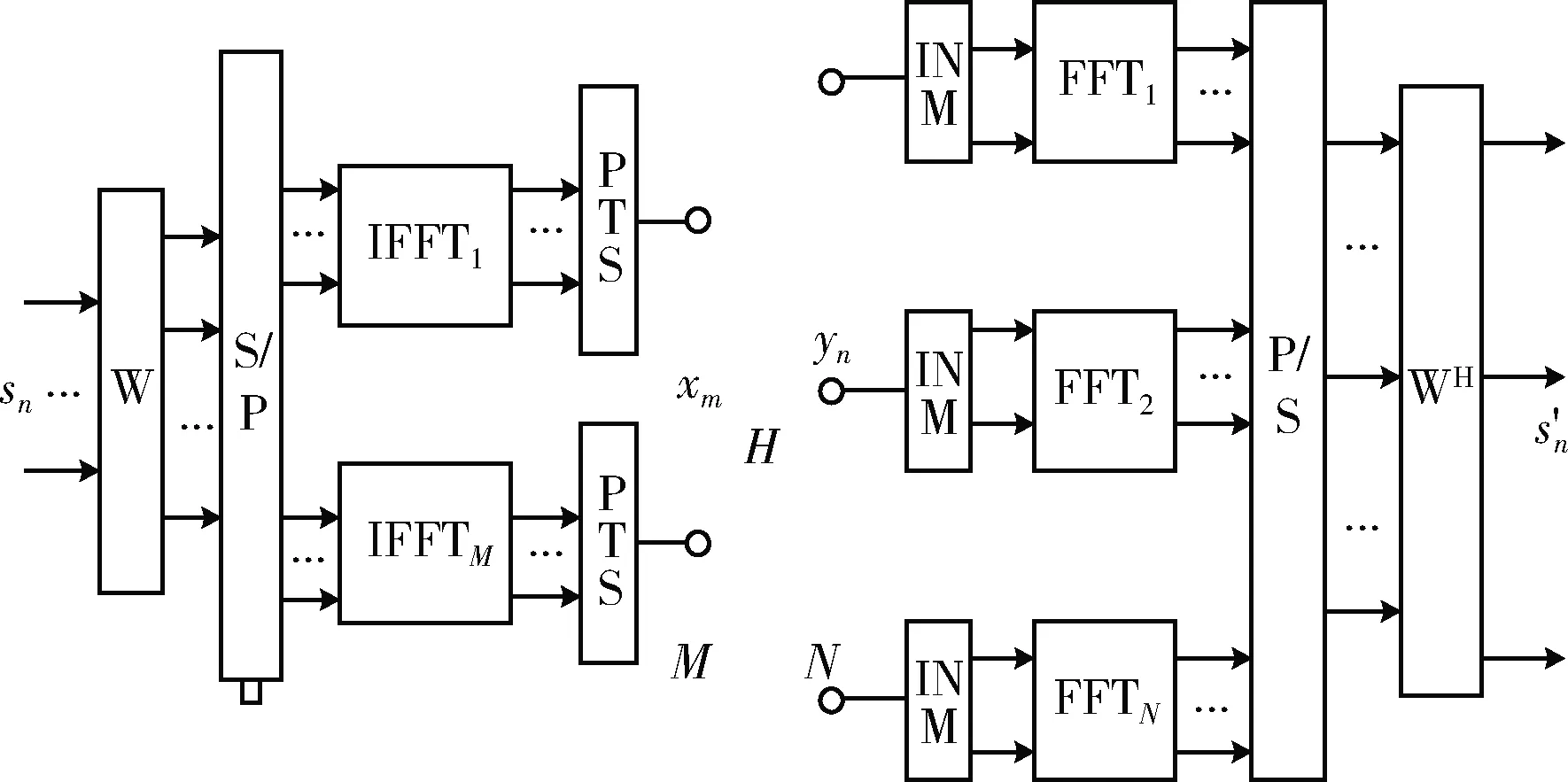
图2 联合PTS的噪声抑制的MIMO-PLC系统模型
文献[5]提到,对于单输入单输出(single-input single-output,SISO)的PLC系统,其频率响应函数可以表示为各个分支路径上的传输函数的线性加权和
(1)
其中,gk是第k条传输通道的传输比例系数,由于电力线传输通路上的环境多变且复杂,信号会多次出现反射的情况,出现次数越多,gk就会越小。α0、α1为电力线媒介的损耗参数、β为指数衰减因子,通常有0.5≤β≤1。dk是第k条传输通道的电力线介质的长度,τk是第k条传输通道的平均时延,它们有如下关系
(2)
其中,vp是电磁波在PLC系统中传播的速度,而vp的数值主要由其在传播媒介中的磁导率μr以及介电常数εr共同决定。
由于电力线的最初设计目的是用于传输电能,其网络结构通常来讲是稳定的,且在一定程度上呈现对称的特点,因此,子信道与子信道之间存在很强的关联性,将一个个子信道组合起来便可以得到MIMO-PLC的信道[6]。如图2所示的MIMO-PLC系统,将其信道矩阵描述为
(3)
其中,hn,m(m=1,…M,n=1,…,N)为第m个传输端口到第n个接收端口的信道传递函数系数,且有
(4)
其中,各参数表示的物理意义与SISO-PLC信道一致。
将图2所示的PLC系统视为2×2的MIMO-PLC系统,有两个发射机和两个接收机,则信道矩阵H为
(5)
1.2 噪声模型
MIMO-PLC系统受到的干扰通常是背景噪声和脉冲噪声[7]。背景噪声划分为有色背景噪声和窄带干扰噪声;脉冲噪声划分为周期性脉冲噪声和突发随机脉冲噪声。前者幅度随时间变化缓慢,对电力线通信干扰相对较小;而后者随时间变化迅速,主要来源于电力线网络中用电设备的突然启动和断开,其持续时间短、强度高、干扰性更强,极易造成通信系统发生突发误码。
结合文献[7]的工作,脉冲噪声可以建模为一个非重复且具有无限状态的周期稳定的马尔可夫过程。因此,状态集为
U=[μ0,…,μη,…μΘ]T,0≤η≤Θ
(6)
其中,Θ(Θ→∞)是总的状态数量。
根据系统的无记忆性特性,状态转移概率为
pkj=Pr(Sl+1=μk|Sl=μj)
(7)
其中,Sl代表系统在时刻l的状态,pkj是系统在时刻l处于状态μj,在l+1时刻转移到状态μk的状态转移概率。其次,马尔科夫过程的状态概率为
(8)
其中,G是脉冲指数,它取决于单位时间内脉冲的平均数。
文献[7]还提到,利用统计特性分析,脉冲噪声的概率密度函数(probability density function,PDF)为
(9)
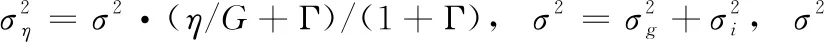
故再结合文献[8]的工作,用混合高斯噪声模型对信道噪声建模
z=zg+zi
(10)
其中,zg是高斯噪声,zi是脉冲噪声。
2 联合PTS的脉冲噪声抑制技术
在前人的研究中,噪声抑制研究的注意力主要都集中在接收端的处理。发射信号经过信道加上噪声后,在接收端通常根据信号与噪声的时频域差异,有针对性的将接受信号中的噪声滤除。而本文中将在发射端对信号采用PTS技术进行预处理,以改善接收端的噪声抑制性能。
考虑在发射端引入PTS技术,其原因主要在于,MIMO-PLC系统是多载波通信系统,发射信号经过IFFT后,所有子载波相加导致峰值很大,对比普通单载波系统,其峰均比很大,导致使用Blanking-Clipping技术降噪时,出现脉冲噪声与信号功率相近而将信号误视为噪声去除的情况,极大影响了其降噪性能[8]。针对上述情况,本文提出了联合PTS-Blanking-Clipping的脉冲噪声抑制技术。
图3为PTS-Blanking-Clipping技术流程。信号经16QAM调制,后经快速傅里叶逆变换,再由PTS技术降低信号的峰均比后发射。在信道中收到噪声影响,在接收端通过Blanking-Clipping技术降噪,再进入解调模块。
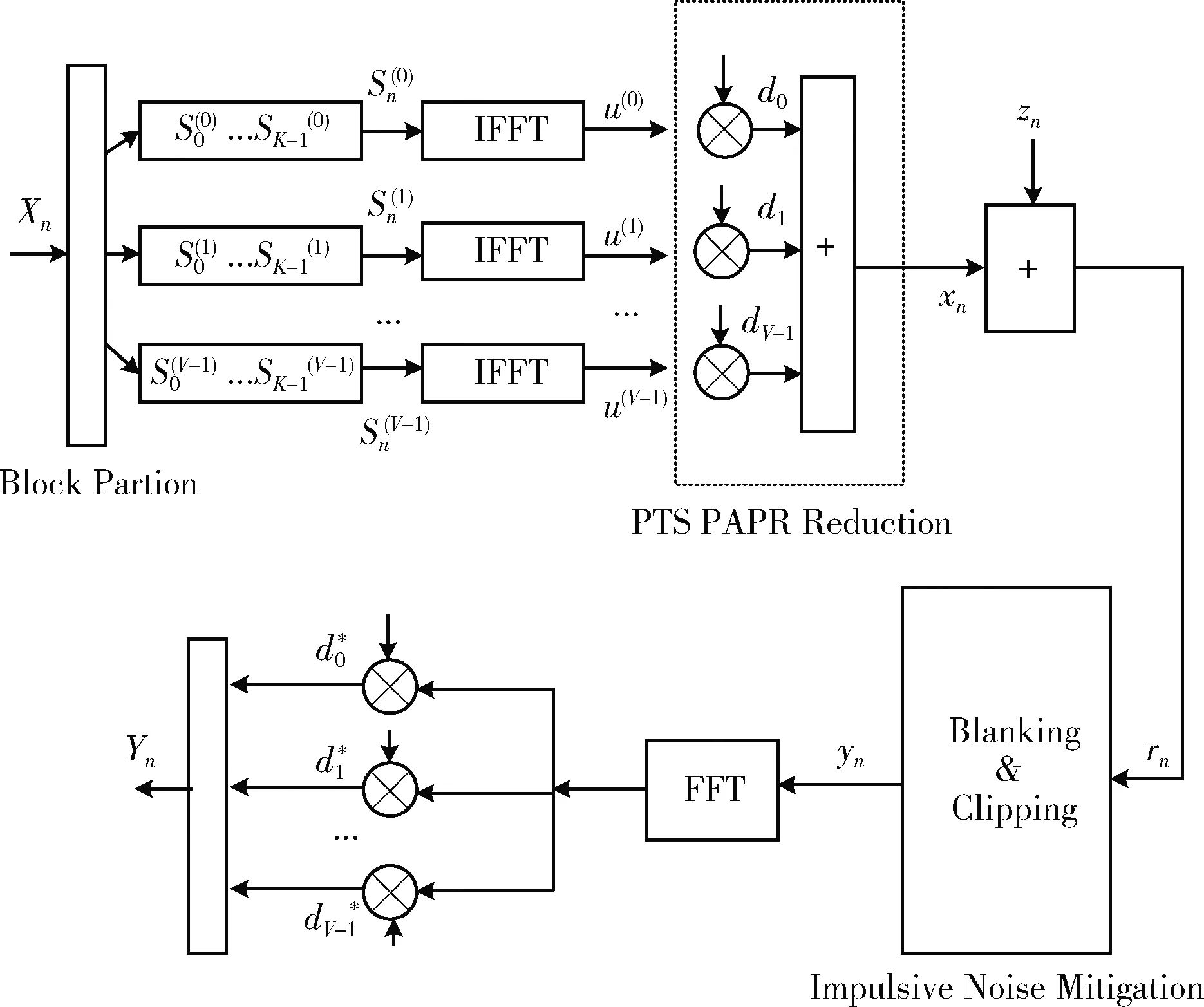
图3 联合PTS的脉冲噪声抑制原理
在进行PTS技术处理前,传输的信息位需要分割成向量。将传输到第n个端口的信息Xn划分为V个互不相交的子块。系统的子载波数为K,因此向量Sn(v)可以表示为Sn(v)=[S0(v),S1(v),…,SK-1(v)],v=0,…,V-1。
经过IFFT变换后的时域信号u(τ)可以写成
(11)
其中,K为子载波数,sk为输入QAM符号,Ts为活动符号间隔,Tp为周期。
2.1 PTS技术
由于系统信号的PAPR通常比较大,接收到信号的功率往往大于脉冲抑制所设定的阈值。因此,高的PAPR会导致不能完全识别脉冲噪声,在后续进行脉冲噪声抑制技术处理信号时可能导致有用的信号被置零、限幅或被忽略,这都会引起噪声抑制技术的性能下降。因此,降低信号的PAPR尤为重要,而PTS技术可以显著降低PAPR且实用性较强[9]。
信号的PAPR定义为
(12)
其中,E(·)表示统计期望,u(τ)表示经过IFFT之后的信号。
PTS技术的基本原理是将输入数据向量Xn划分为V个互不相交的子块Xn=[S(0),S(1),…,S(V-1)],然后子向量S(v)中的每个子载波乘以复杂相位系数dv,且满足
dv=ejφv,(φv∈[0,2π])
(13)
将相位系数序列对V个子向量进行加权合并再进行IFFT变换后有
(14)
其中,xn为经过PTS方法降低PAPR后的发射端信号,然后在所有的复杂相位系数组成的集合当中,采取无穷枚举的方式找出最优的复杂相位系数d′v,从而使序列中xn的峰值最小,即有
(15)
其中,argmin(·)表示函数取得最小值时所使用的依据条件,据此,得到最佳序列xn为
(16)
2.2 脉冲噪声处理
Blanking技术是抑制脉冲噪声最简单的方法[2],但当信号的PAPR偏大时,极易出现将有用信号误视为噪声从而去除的情况,在信号与脉冲噪声之比 SINR较小时,性能较好;Clipping技术的本质是将信号限定在一定幅度以内,相较于Blanking技术对低功率脉冲噪声有更好的辨识度,在SINR较大时,性能较好;Blanking-Clipping技术兼顾了两者的优点。
结合Clipping和Blanking方法实现脉冲噪声处理,需要设定两个振幅阈值[9],置零阈值T和限幅阈值aT,a通常是一个大于1的常量。基于此,在接收端分3种情况对经过信道后的信号rn进行降噪处理:
(1)第一种情况记为D0,当接收信号的幅度在0到T之间,此时接收到的信号是几乎不受脉冲干扰的传输信号,此时,无需对其进行处理。
(2)第二种情况记为D1,即接收到的信号幅度在T和aT之间时,需要对信号进行限幅,arg(rn)表示r0,…,rK-1中输入信号幅度的最大值,此时,将Tejarg(rn)作为限幅后的输出信号。
(3)第三种情况记为D2,当接收到的信号幅度大于aT时,将其视为脉冲噪声采取置零处理,信号置为0。
根据上述描述,Blanking-Clipping技术处理后的输出信号可以表示为
(17)
根据文献[10]提到,式(18)中的κ可以表示为
(18)
经过文中所提技术处理后输出信噪比(signal to noise rate,SNR)可以表示为
(19)
其中,Pout和κ分别是经过混合降噪处理的输出信号功率和比例因子。
在经过噪声处理后,信号的功率Pout可以表示为
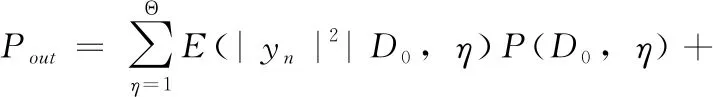
(20)
其中,P(D0,η)为η状态下D0发生的概率,P(D1,η)为η状态下D1发生的概率。
文献[10]提到,PLC信道的衰减服从对数正态分布,即有
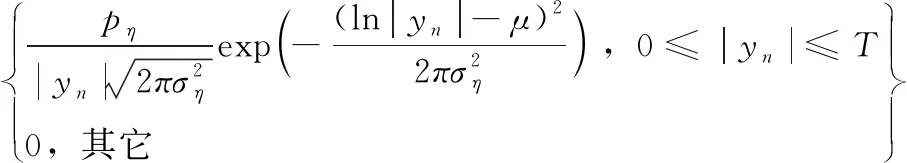
(21)
由此概率密度函数,可以得到η状态下D0发生的概率

(22)

P(D0,η)=pηQ(T)
(23)
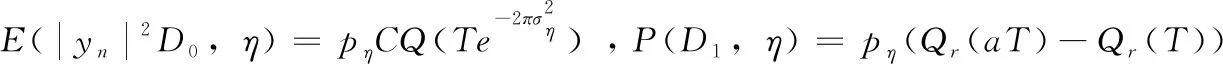
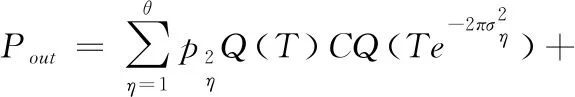
(24)

3 仿真结果及分析
为了验证本文提出的联合PTS-Blanking-Clipping脉冲抑制技术的性能,使用MATLAB软件对MIMO-PLC系统进行了蒙特卡罗仿真,仿真参数选择基于Home Plug AV2.0标准[11],具体的系统仿真参数参见表1。

表1 系统仿真参数
为了评估所提出的PTS-Blanking-Clipping技术的输出信噪比,需要为式(17)选择合适的阈值,然而,阈值的最优值在理论上很难确定,故采用实验方法来确定一个相对最优阈值。如图4所示,当阈值设定太小,大部分有用信号会被误视为噪声而去除;当阈值大于6时,大量小功率脉冲噪声会被忽略,从而引起信噪比显著下降。当阈值小于2,采用Clipping技术可获得最优信噪比;当阈值设定为2或者3时,采用Blanking技术可获得最优信噪比,而当阈值更大后,PTS-Blanking-Clipping技术的输出信噪比则有明显优势。因此设定式(19)中的T=3,aT=4。

图4 不同阈值下几种噪声抑制技术输出信噪比比较
图5为引入PTS后的输出信噪比对比。如图5所示,将信号通过PTS技术处理后再进行降噪,系统的输出信噪比更高,且V=8时其输出信噪比更高,其中V为分块数,原因在于PTS技术中得到最优序列的准确性与V值在一定范围内呈正相关性[12]。阈值大于4时,采用PTS的混合降噪技术比未采用PTS的输出信噪比大约高0.5 dB~1.0 dB。当选择合适的阈值时,如T=3(V=8)时,基于PTS的脉冲抑制技术的输出信噪比比未引入PTS之时提高了1.9 dB。
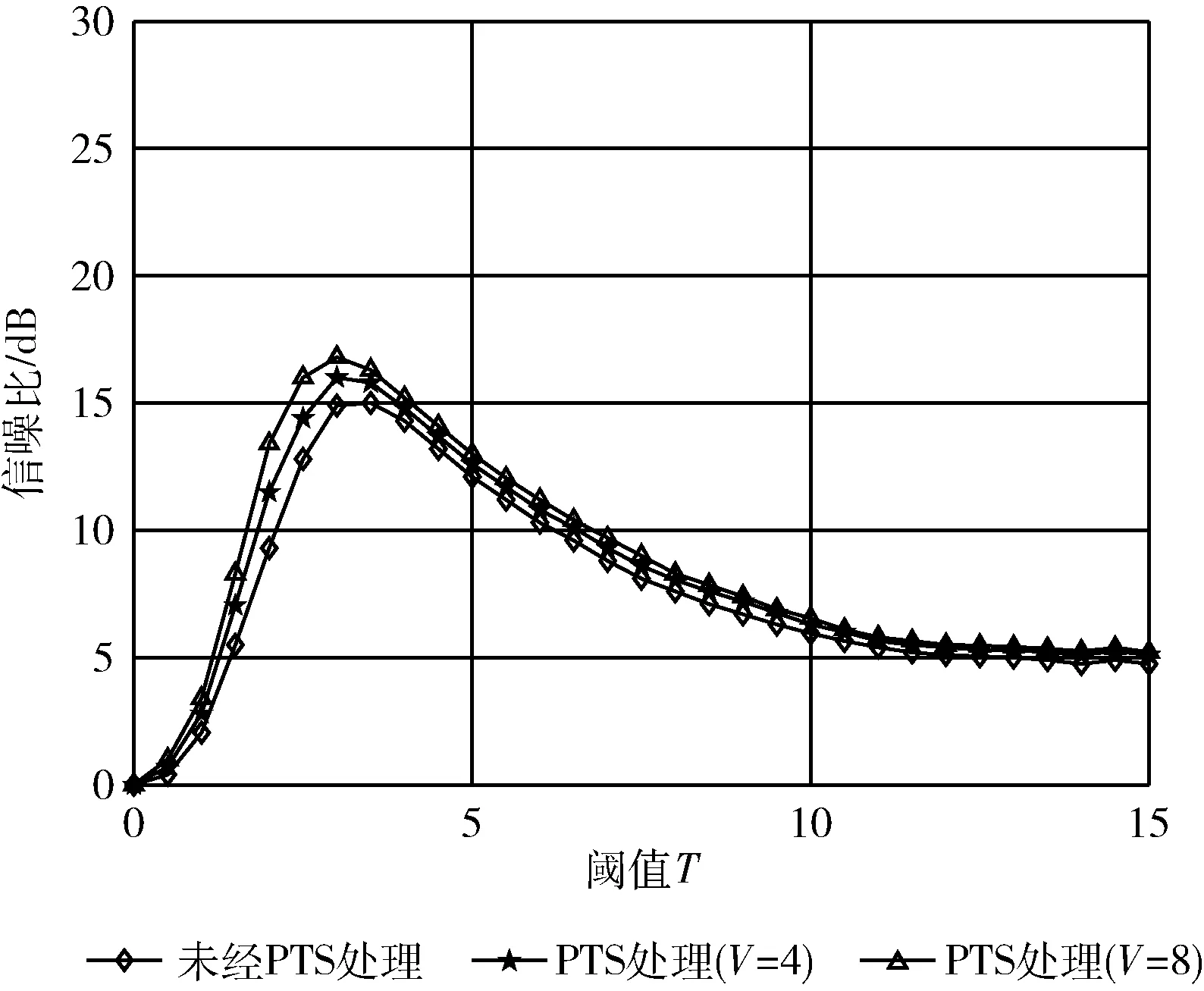
图5 未引入和引入PTS技术后的输出信噪比对比
图6为不同信号与脉冲噪声之比SINR下的各种技术的误码率比较。当SINR较小时,Clipping技术性能较差,且明显不如其它几种技术,因为此种情况下脉冲噪声与信号区分度不明显导致限幅效果不好误码率较高。当SINR小于-14 dB时,本文所提PTS-Blanking-Clipping技术性能明显优于传统Clipping和Blanking技术,而SINR更小时,脉冲噪声功率与信号相差很大,采用置零方式已有较好性能,所提技术性能提升不明显。在SINR为-12 dB至-5 dB 时,PTS-Blanking-Clipping技术性能提升最为显著,相较于Blanking-Clipping技术,误码率降低了约2%,因为此时PTS降低了信号峰均比,使信号功率明显小于脉冲噪声以便于进行阈值判决,从而显著提高了误码率性能。
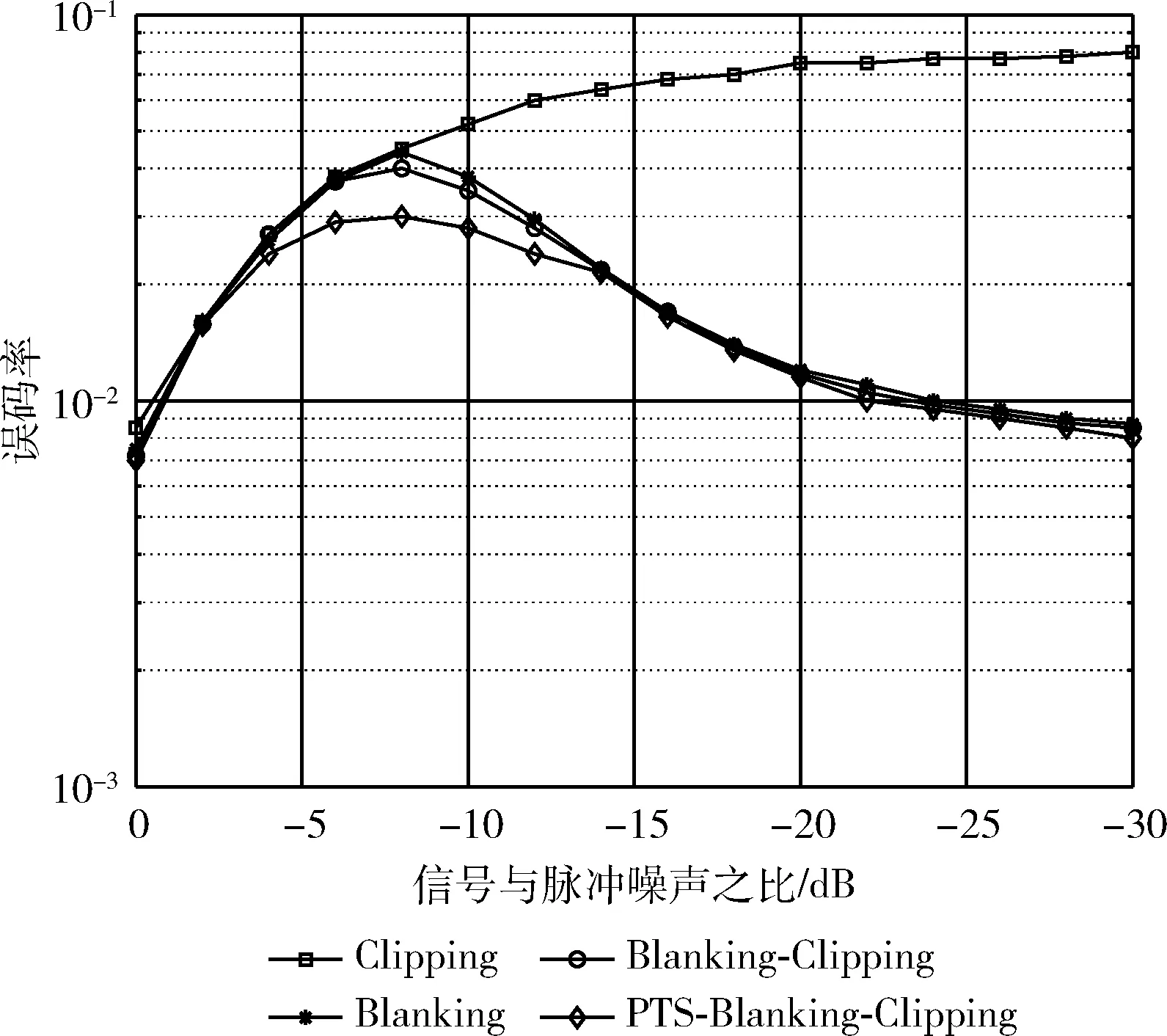
图6 传统方法和所提方法在不同SINR下的误码率比较
4 结束语
本文针对PLC信道存在脉冲噪声干扰严重的问题,提出了一种联合PTS的脉冲噪声抑制技术来降低信道脉冲噪声,以提高通信可靠性。为了解决Blanking-Clipping技术容易将较大功率信号误去除的缺陷,引入PTS技术降低传输信号的PAPR,并确定两个相对最优阈值以提高PTS-Blanking-Clipping技术的降噪性能。仿真结果表明,与Clipping、Blanking和未引入PTS的Blanking-Clipping技术相比,所提技术可以显著提高输出信噪比,降低误码率,改善系统通信性能。
