基于有限元法的工字形结构安全优化设计

谭凯军 程赫明

(昆明理工大学建筑工程学院 昆明 650500)

0 引言

最优化就是追求最好的结果或最优的目标。优化设计主要指在一定范围内的设计方案中选择较佳的设计方案，而通过一定的策略搜索到最优设计方案的过程就是最优化设计法,这种策略使用到的数学理论就是最优化设计理论[1]。结构优化设计基于理论力学基础和数学优化理论,根据实际需要,优化设计的参数以变量形式出现,组合成可行的结构优化方案集合,再用数学思路在集合中找出满足既定的，不仅可行而且效能与安全性高的设计方案。实践表明，结构优化设计不但能缩减产品设计周期,而且还能提高产品质量和水平,与初始设计方案相比,优化后方案普遍能把造价降低5%～30%[2]。

上海工程技术大学的张召颖等[3]建立了T形结构模型，通过ANSYS下的Topology Optimization 模块对T形结构拓扑优化。山东建筑大学的汤爱君等[4]通过Ansys Workbench软件对低位缠绕机链轮支架进行静态特性分析以及拓扑优化。湖北工业大学的景修润等[5]使用Ansys Workbench对铆钳弯臂进行受力分析找出危险截面并验证，将模型参数化选取优化参数，再对参数尺寸优化设计，从而节约生产成本。目前优化设计主要分为3类，其中结构拓扑优化在当前优化应用体系中优化效果最好，是发展迅速并且难度最高的一种高效优化设计。连续体拓扑优化的方法有：连续体结构均匀拓扑优化法[6]、改进的均匀化法[7]、渐进结构优化法[8]、水平集法[9]等。离散型拓扑优化有：程耿东教授的松弛方法[10]、基于遗传算法的拓扑优化[11]等。

如今由于拓扑优化的优越性，拓扑优化方法在工业生产与生活领域中的应用越来越普及。通过有限元变密度拓扑优化设计，限定非设计区域，对工字形结构设计区域展开拓扑优化设计，在满足安全性与可靠性设计的前提下，合理优化工字形结构材料的空间几何分布，从而实现工字形结构在工业安全生产领域的拓扑优化设计。

1 结构静力分析

建立三维数学模型，通过Workbench软件相容性对接导入有限元静力分析模块，设置材料参数、划分三维模型网格、输入约束条件、施加载荷，再对结果应力和形变进行静力分析。

1.1 简化有限元模型

选取标准工字形结构通过三维设计有限元Workbench软件建立三维模型，该工字形结构三维造型及几何尺寸如图1所示，材料属性主要参数如表1所示。

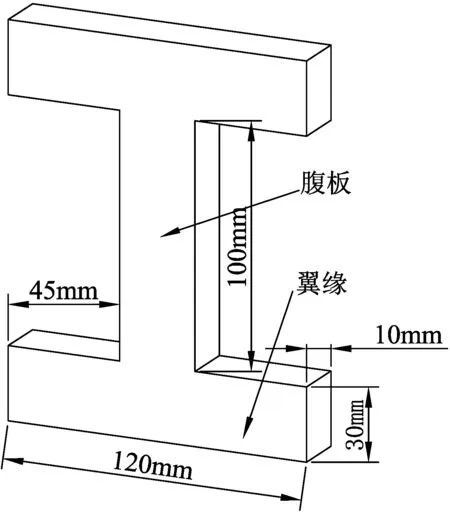
图1 结构几何尺寸

表1 结构材料各项参数

用正六面体单元划分出有限元模型网格，得到13 195个节点、2 532个单元。上侧翼缘左右2孔洞固定约束，下侧翼缘2孔洞内各受向下集中荷载36 N，腹板与翼缘相交处做圆滑处理。结构模型约束面与施加集中荷载位置见图2。

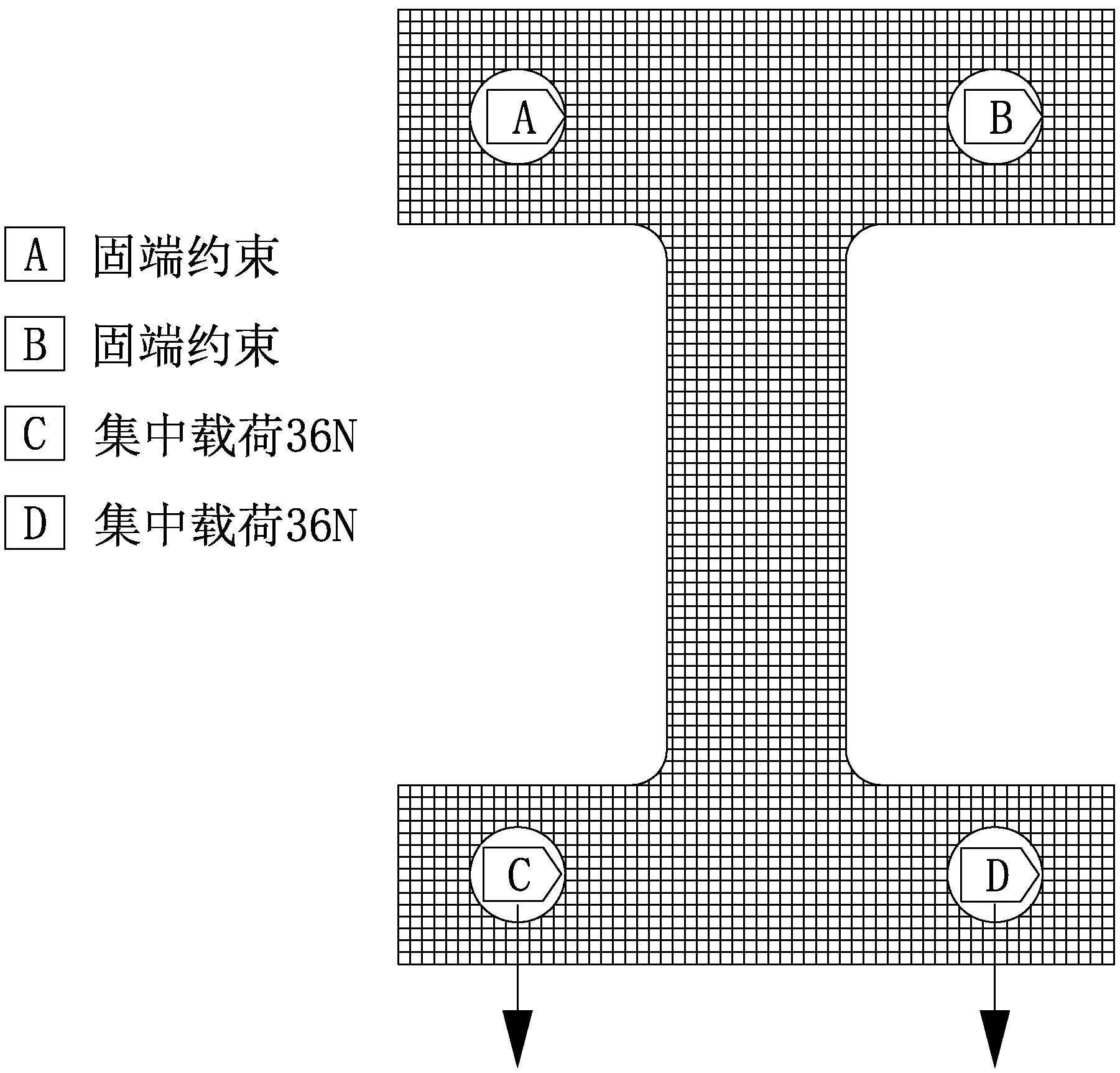
图2 结构网格划分

1.2 有限元静力分析

通过Workbench下的静力分析模块对结构载荷分析，得到有限元模型的基本位移云图，如图3所示。由图3可知：在载荷作用下最大位移0.000 182 99 mm，最大位移产生在下部翼缘边缘处，最小位移发生在固定圆孔内侧处；结构形变具有对称性，由于结构与施加荷载都具有对称性，表明位移云图符合实际工况。由结构等效应力云图(见图4)可知：结构腹板应力较为均匀，在结构下翼缘与腹板直角处存在应力集中效应，所以该处应力值最大为0.417 77 MPa，因为上部翼缘边缘两侧处不存在荷载与约束条件作用，其应力最小。

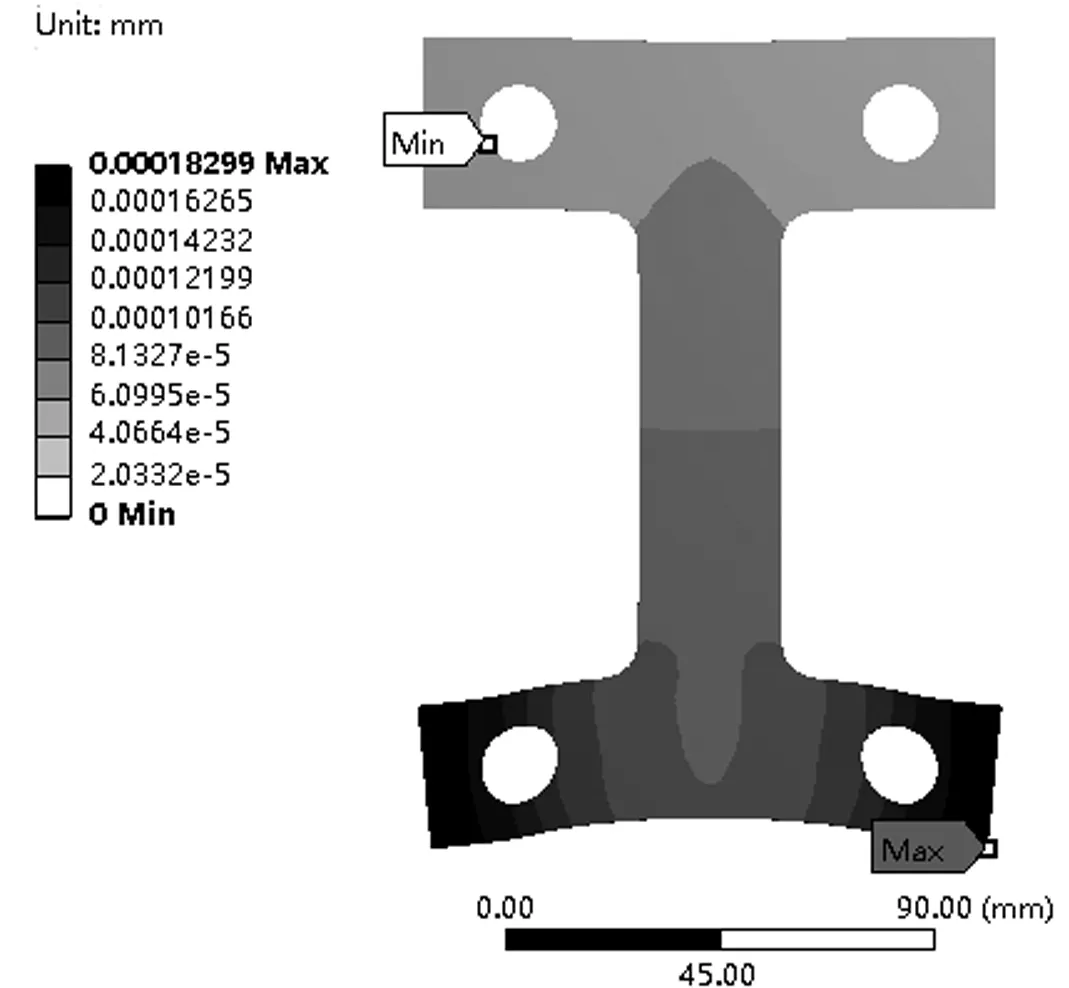
图3 结构位移云图

图4 结构应力云图

2 结构拓扑优化

2.1 建立拓扑优化数学模型

考虑到结构密度过小会导致迭代时间过长或者求解不出最优解，以最小质量为整体结构的目标函数，以质量减少百分比、许用最大应力、许用最大形变为约束条件，通过有限元技术[12]优化工字形结构。在满足结构基本稳定等条件下拓扑优化，工字形结构几何优化的数学基本模型求出如下：

式中，f(M)为目标函数；M为结构优化后的质量；M0为结构初始化质量；α为质量约束百分比；σ为优化后最大位移；[σ0]为结构许用位移；δ为优化后最大应力；[δ0]为结构许用应力。

2.2 拓扑优化步骤

结构拓扑优化主要流程如图5所示，建立符合实际的物理模型，选定优化目标、规划约束条件；然后把建好的模型通过软件相容性导入有限元Workbench软件静力分析模块对结构静力分析，确定拓扑优化数学模型，规划拓扑优化约束条件；设置拓扑迭代次数，展开迭代，验证结果是否满足最大许用应力与最大许用形变边界条件；优化后处理模型，检验结果优化后保证满足许用应力与许用位移等约束条件；最后再对结构质量约束百分比验证，如若满足，结束拓扑优化。

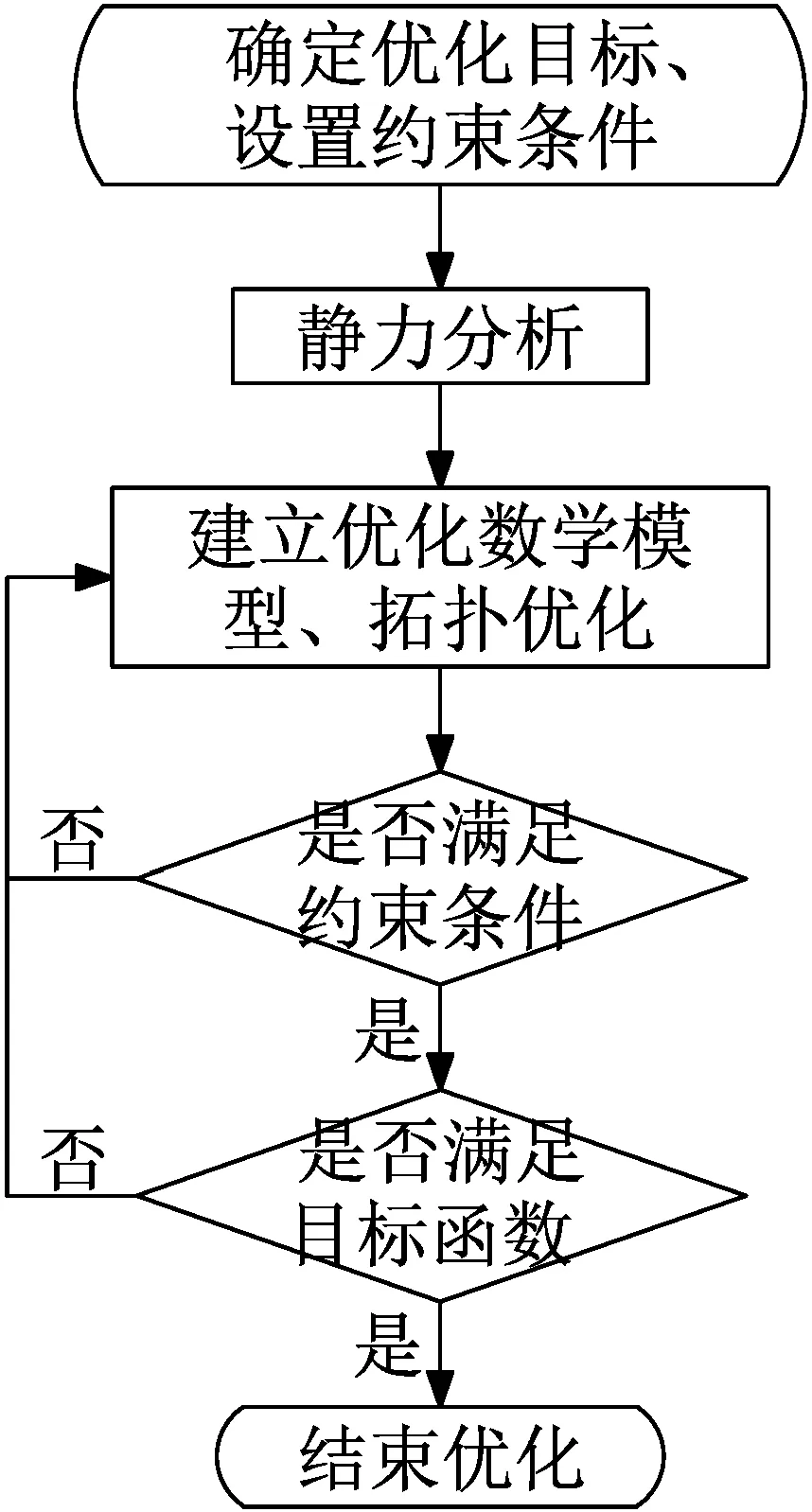
图5 拓扑优化流程

2.3 实例拓扑优化

4个孔洞位置均为非设计区域，在求解过程中保留该区域特征。拓扑优化设计区域为模型结构非约束区域的其余区域，整体结构的质量为目标函数，约束条件分别为[σ0]=1 MPa，[δ0]=0.000 2 mm,目标质量分数为50%。迭代30步收敛容差0.2%，惩罚因子2，通过有限元软件计算得到结构优化迭代过程的结果如图6和图7所示，从迭代曲线图与收曲线图中分析可知优化迭代目标总体趋于收敛，表明满足优化方案条件。

把优化后的模型圆润处理，在相同条件下静力分析，得出优化后模型变形云图(图8)与应力云图(图9)，从应力云图中可以看出结构主要变形产生在应力孔洞外侧区域，应力在腹板处分布较为均匀，最大应力在下部翼缘与腹板相接弯曲折角处。优化设计后的结构载荷路径与结构变形较为合理，与优化前的结构主要集中形变与应力位置并无太大变化，表明拓扑优化后的结构较为理想。

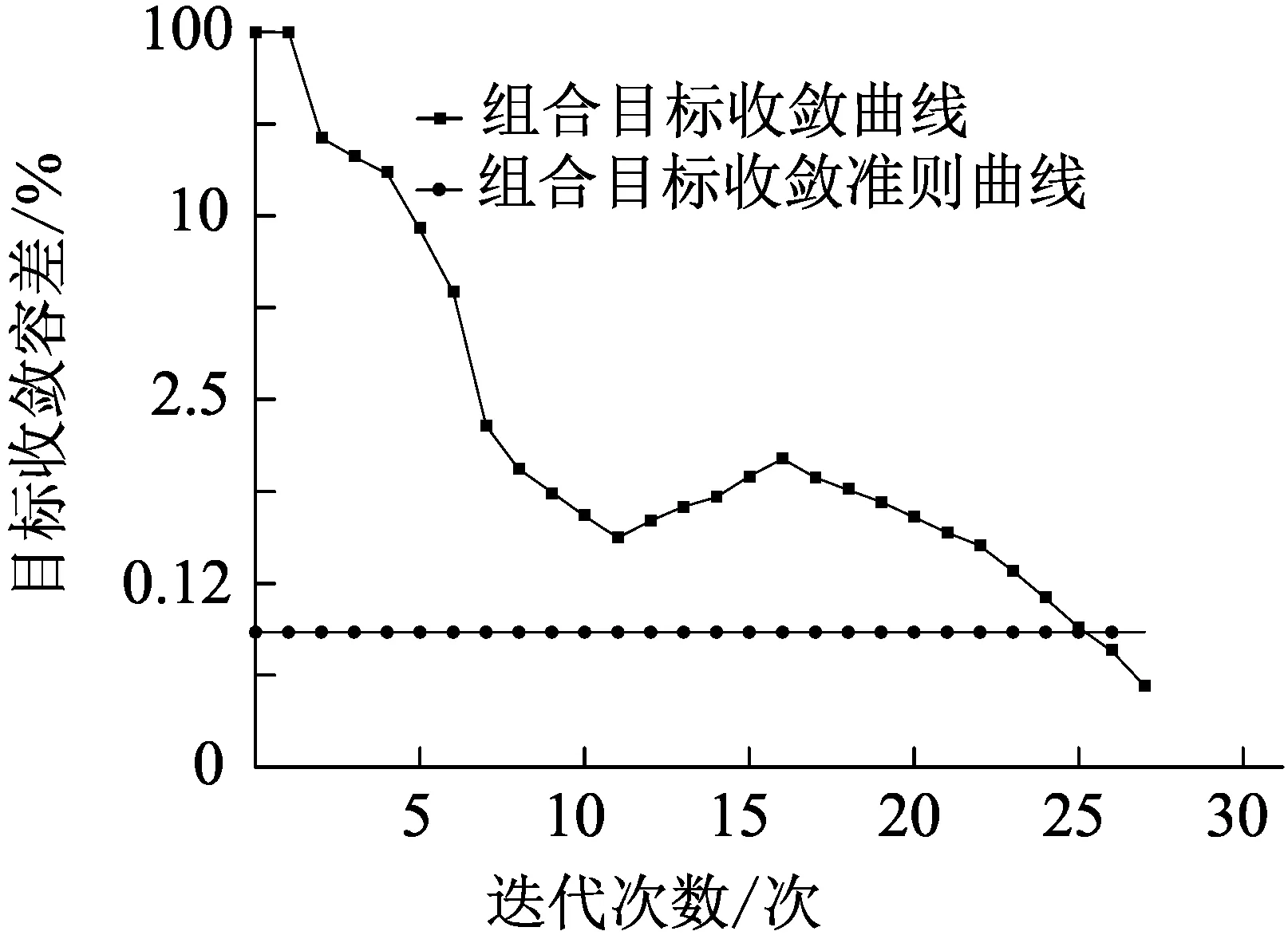
图6 结构迭代曲线

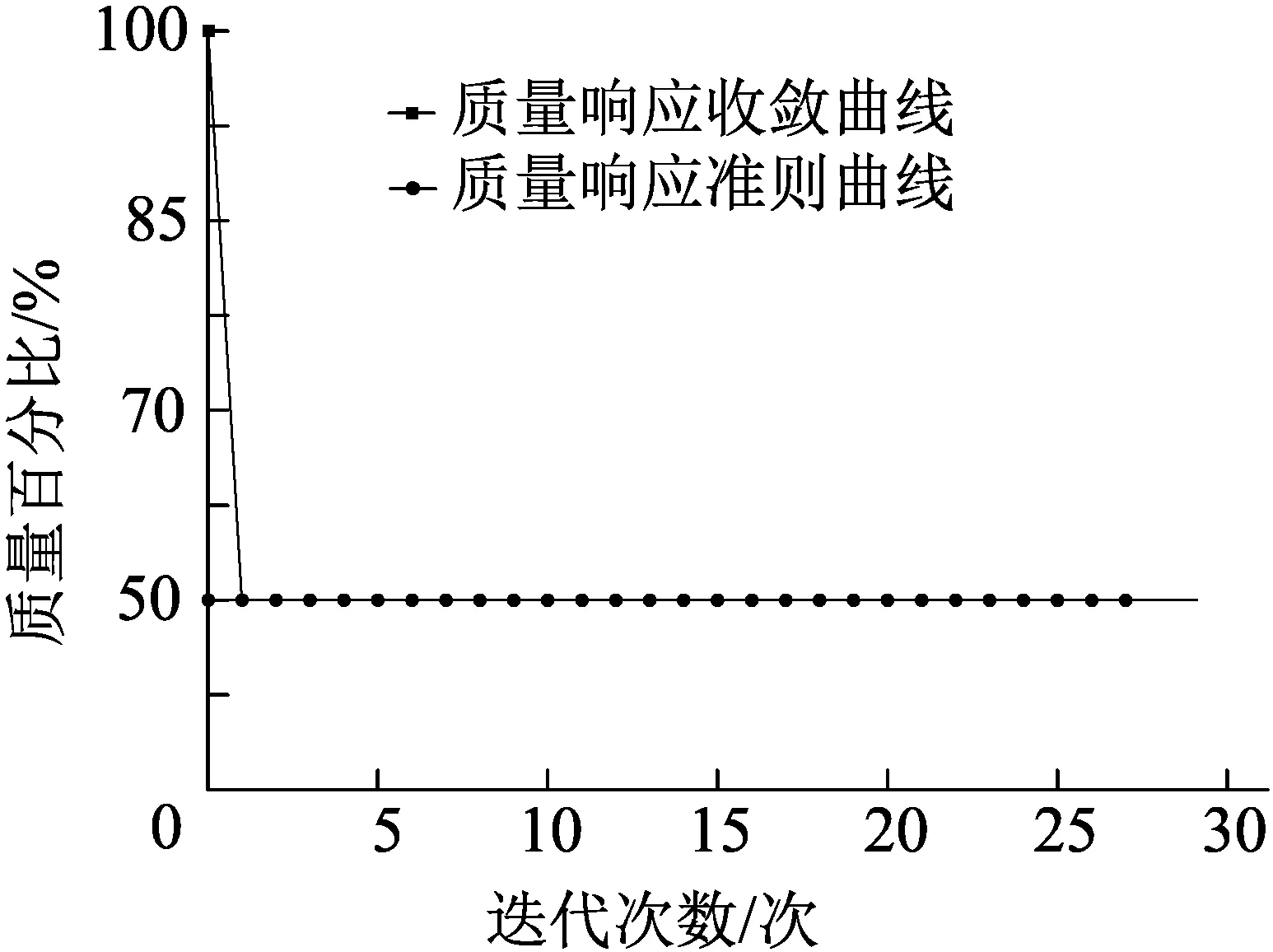
图7 结构收敛曲线

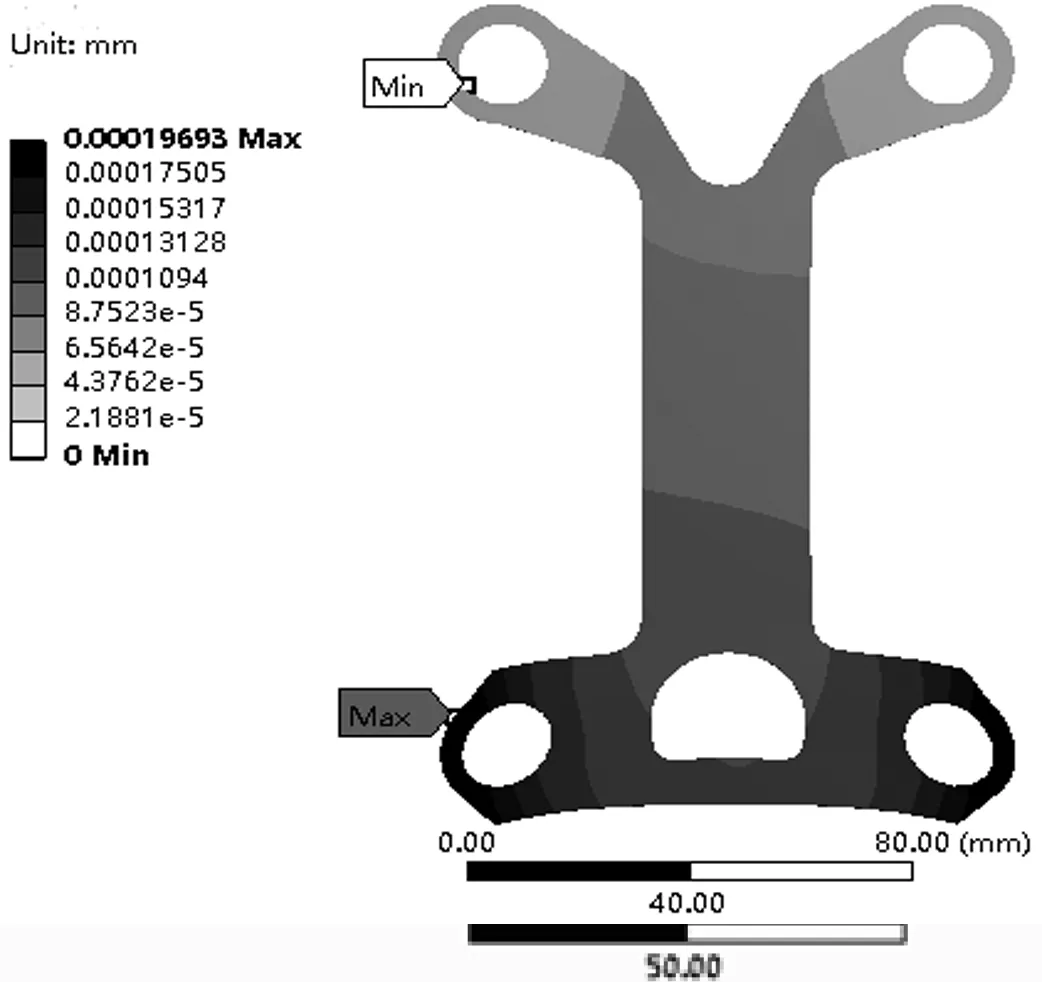
图8 优化后变形云图

3 优化后性能对比分析

表2为工字形结构优化前、后的各项参数对比，由表2可知：拓扑优化后工字形结构的参数指标分别增加0.000 01 mm与0.193 1 MPa，增加幅度不大，质量降低38%，均在安全设计允许范围内。

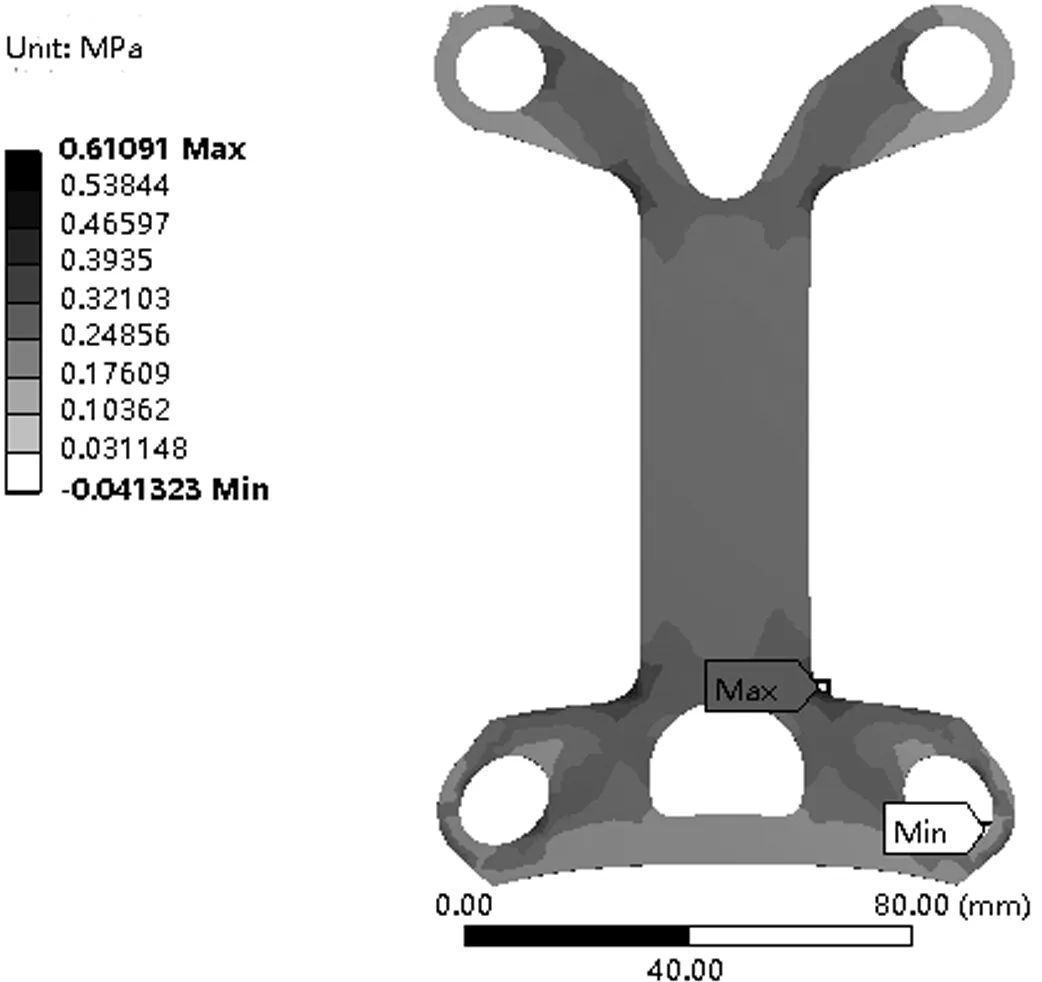
图9 优化后应力云图

表2 拓扑优化前后性能对比

4 结论

通过对工字形结构拓扑优化设计前、后的性能对比可以看出，拓扑优化在工业结构安全优化领域具有非常广阔的发展空间与前景，与此同时优化后的结构不但极大地节省了材料，提高了安全性能，荷载与变形结构也更加合理，为设计工作者的研究与设计提供了一个比较好的方法与思路。