基于轮廓测量的集料表面粗糙度表征方法试验研究*

刘春阳 李洛克

(昆明理工大学建筑工程学院 昆明 650500)

0 引言

当前，道路对路面性能要求日益增多，对道路安全性、环保及资源再利用等要求持续提高。路面材料的适用性、安全性、组成设计等对路面的使用性发挥着关键作用。在道路工程领域，沥青材料具有可再生利用的优势，岩石集料为普遍采用的原材料，其表面纹理的粗糙程度会显著影响沥青混合料的路用性能。粗糙的纹理表面有利于增大集料与沥青的接触面积，形成一定的胶结料渗透深度，增加沥青膜的厚度，增强两种材料在接触面上的物理吸附作用。同时，集料颗粒轮廓面的细微凸起较多，有利于在拌和过程中形成相互嵌挤的骨架结构，使沥青混凝土具有良好的抗剪强度，提升路面的抗车辙性能。因此，定量表征岩石类材料轮廓面的粗糙特性，对于改善及提高沥青混合料的路用性能具有实际意义。

近年来，岩石类材料轮廓面粗糙特性的相关研究日益受到关注，如BARTON N使用节理粗糙度系数(JRC)作为评价指标[1]，选取10条典型岩石表面轮廓线评估JRC，其取值范围在0到20之间[2]，如表1所示。在岩土工程研究领域，粗糙度系数常被用于建立岩石表面轮廓形貌与其界面力学及渗流特性的相关性[3-4]。在道路工程领域，粗糙度是分析沥青与集料的黏附性与集料颗粒表面纹理粗糙度关联程度的重要指标[5-6]。现阶段工程领域常采用经验法对集料形貌特征进行评价，如我国现行的《公路工程集料试验规程》中粗集料磨光值试验适用于评价集料的路用耐磨耗、抗滑等性能，但不适宜在微观层次描述集料纹理的粗糙程度[7]。

鉴于此，本文采用粗糙度系数JRC对集料表面纹理粗糙度进行定量表征，提出了基于接触式测量的粗集料破裂面二维剖面的评价方法，定性与定量评价粗集料破裂面二维剖面。在此基础上，分析集料表面二维轮廓线粗糙度的各向异性特征，提出集料表面三维轮廓面粗糙度的评价指标，构建基于轮廓测量的集料表面粗糙度表征方法，进一步试验验证方法的可靠性。

表1 Barton标准粗糙度轮廓线

1 集料表面二维轮廓线粗糙度评价方法

采集粗集料破裂面表面的二维剖面轮廓线，分别运用定性与定量方法评估粗糙度，提出了适合工程应用的二维粗糙度测量方法及模式。

1.1 Barton标准剖面法

在粗集料表面测试区域内选取等距的9个观测截面，如图1所示。应用Kasaka FGA51型触针式轮廓形状分析系统采集粗集料观测截面断面的纹理表面起伏轮廓线。首先，设置触针移动速度为0.5 mm/s，波动范围控制在±0.02 mm/s，采样步长为2 μm，采样直线距离为12 mm。其次，在对有效测试长度10 mm内的数据进行滤波处理并数字化的基础上，将其等比例绘制于坐标网格中。最终，通过与Barton标准轮廓线的目测比较来确定集料二维剖面测试轮廓线的JRC，如表2所示。

由上述粗糙度评价过程可以看出，通过Barton标准剖面法虽可以在特定剖面提取粗糙度特征，定性评价粗集料表面纹理，但受轮廓曲线采集精度、应用经验等因素影响较大。同时，受岩性与生产工序影响，岩石类集料表面纹理的形貌特征差异明显，仅根据与标准轮廓线目测对比以确定集料二维剖面测试轮廓线的粗糙度存在较大误差。

图1 集料表面观测截面

表2 基于Barton标准剖面法的轮廓线粗糙度评价

1.2 特征参量表征法

为定量分析岩石类材料二维剖面轮廓线的粗糙度，以贯穿于取样长度内的一条最小二乘中线作为基准线，建立几何特征统计参数与粗糙度间的回归方程计算JRC值，进一步提取分析轮廓曲线的起伏特征信息，如图2所示。

图2 二维轮廓线起伏幅度示意

根据纹理轮廓线与基准线间的关系，获取表征粗糙度的相关参数，主要包括轮廓线总长度、轮廓线幅度函数、轮廓线正向坡、负向坡总长度等。但由于上述参数基准线位置是影响其结果的重要因素，在实际操作过程中，寻找最小二乘中线较为困难。因此，根据不受基准线位置影响的结构函数SF与粗糙度系数间的关系[8-9]，定量计算集料二维剖面轮廓线的粗糙度JRC2D：

JRC2D=37.28+16.58lgSF

(1)

(2)

式中，L为表面轮廓线总长度；y(x)、f(x)均表示表面轮廓线幅度；△xi为轮廓线L在X轴方向上测点间距(X轴方向上测点间距为2 μm，即△xi=0.002 mm)。

根据测量曲线相对坐标数据，计算集料破裂面9条二维轮廓线的粗糙度系数JRC2D，如表3所示。

表3 基于特征参量表征法的轮廓线粗糙度评价

计算结果表明，采用特征参量表征法可以定量表征集料纹理的二维剖面的粗糙度系数，但对集料纹理起伏形态的几何特征参数测量精度要求较高。在工程应用中，受测量条件及统计规模的限制，使用起伏度特征参数表征法对集料表面纹理粗糙度的评价能力十分有限。

1.3 迹线长度表征法

在实际工程应用中定量评价路用岩石类集料的粗糙度系数，首先要满足精度要求，同时测量仪器、试验方法及计算流程不宜过于繁杂，应具备测量速度快、便于统计分析的特点。因此，在综合比较已有的计算参数后，认为采用SOUDANI S M[10]提出的迹线长度表征法符合以上要求。

(3)

式中，Rp为剖面轮廓线轮廓线实际长度与其直线长度的比值；xi、xi+1、yi、yi+1分别为测试轮廓线第i点和第i+1点的相对坐标。

在不同的采样间隔下，Rp与JRC的函数关系如表4所示[11]。

表4 参数Rp与JRC的函数关系

将表2中各轮廓曲线的测点数据以0.5 mm间隔进行采样后带入式(3)，获取轮廓线的伸长率Rp，再通过表4中采样间隔0.50 mm的Rp与JRC的函数关系式计算每条集料破裂面二维剖面轮廓线的粗糙度系数JRC2D，结果如表5所示。

表5 基于迹线长度表征法的轮廓线粗糙度评价

计算结果表明，使用起伏度特征参数表征法与迹线长度表征法的计算偏差在13%以内，具有良好的相关性。本文中两种粗糙度表征方法计算结果的偏差主要是由采样间隔差异引起的，通过特征参量表征法计算时采样间隔为0.002 mm，通过迹线长度表征法计算时采样间隔为0.5 mm。在相对较大的采样间隔下，测量曲线的部分细观形貌变化无法采集，导致计算的粗糙度数值总体偏低。

2 集料破裂面三维粗糙度表征方法

建立集料破裂面的三维形貌数字高程模型，分析了集料表面粗糙度的各向异性特征，提出了集料轮廓面三维平均粗糙度的表征方法。

2.1 粗集料破裂面表面粗糙度的各向异性特征

将粗集料破裂面表面10 mm×10 mm范围作为观测区域，在x、y方向均以0.5 mm采样间隔各设置20个测点，共400个测点，如图3所示。采用轮廓形状分析系统获取测点相对坐标数据后，通过Matlab编程绘制集料破裂面采集区域的三维形貌数字高程模型[12]，如图4所示。

图3 集料破裂面测量区域与测点

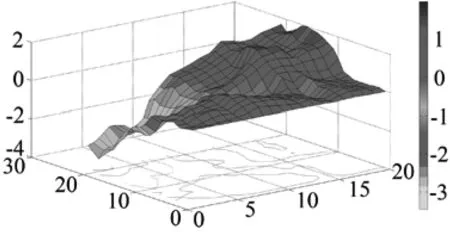
图4 集料破裂面三维形貌数字高程模型

由三维形貌数字高程模型可见，粗集料破裂面剖面的二维轮廓线粗糙度在不同角度方向上具有显著的差异性。在观测区域内定义坐标原点与0°方向；以0°方向为基准线，经过该点每隔15°切一个剖面，将集料破裂面采集区域共切出12个剖面，如图5所示。应用迹线长度表征法分别测算12条二维剖面轮廓线的粗糙度系数JRC2D，绘制集料破裂面采集区域的粗糙度各向异性图，如图6(a)所示。

图5 断裂面12条剖切线平面位置分布

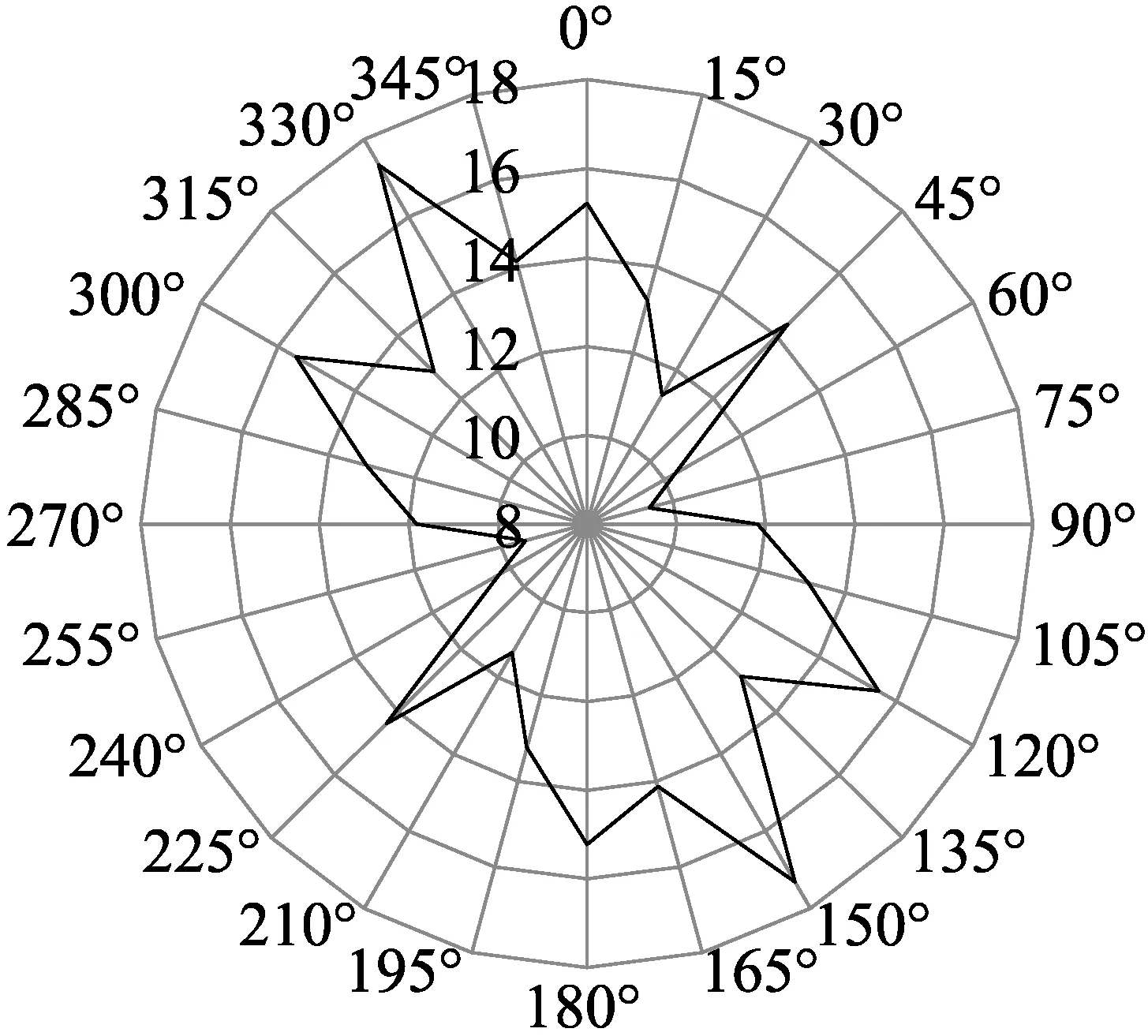
(a)15°间隔各剖面粗糙度变化

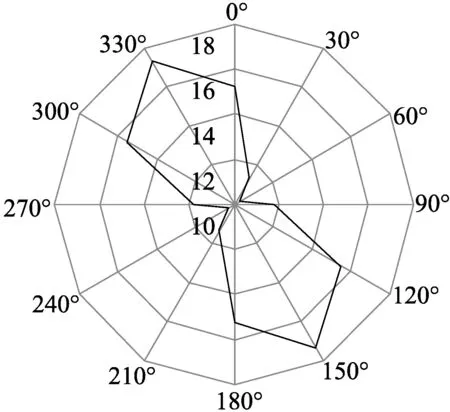
(b)30°间隔各剖面粗糙度变化

(c)45°间隔各剖面粗糙度变化

试验结果表明，集料破裂面采集区域内的12条二维剖面轮廓线粗糙度各不同，并与方向改变无明显关联性，呈现出明显的各向异性特征。因此，二维粗糙度系数不能整体地表征集料表面的几何形态，应使用三维粗糙度系数进一步综合表征集料颗粒轮廓面粗糙纹理的几何特征。

2.2 三维平均粗糙度JRC3D表征方法

鉴于粗集料破裂面表面形态与剖面轮廓线二维粗糙度呈现明显的随机特征，参考学者杜时贵提出的方法[13]，采用求均值方法将测试区域测定的多角度二维剖面轮廓线的粗糙度系数JRC2D扩展为三维粗糙度系数JRC3D，表征粗集料断裂面测试区域内的平均粗糙度，降低剖面线的选取差异导致的测试结果偏差。

(4)

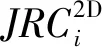
应用式(4)计算图6(a)中测量区域12条剖面轮廓线的平均粗糙度为13.56。为进一步分析剖面轮廓线间隔角度及数量对计算结果的影响，分别取间隔角度为30°、45°，相应的剖面轮廓线数量分别为6条及4条，对应的剖面粗糙度变化如图6(b)、图6(c)所示。

应用式(4)计算图6(b)中30°间隔的6条剖面轮廓线平均粗糙度JRC3D为13.59，计算图6(c)中45°间隔的4条剖面轮廓线平均粗糙度JRC3D为14.57。根据计算结果可以看出，由间隔15°的12条剖面轮廓线与间隔30°的6条剖面轮廓线计算的平均粗糙度JRC3D结果差值分别为2.8%及7.4%，其余试样也体现相关规律。可见，当剖面轮廓线间隔小于30°时，计算结果较为稳定。进一步考虑试验效率与评价精度，建议测试剖面夹角取为30°，对应的测试二维剖面轮廓线数量n为6。

3 基于JRC3D的粗集料破裂面粗糙度评价

选取平均粗糙度JRC3D作为评价指标，提取道路工程中常用集料表面的粗糙度特征，深入分析在不同磨光程度下集料轮廓面的粗糙度变化情况。

3.1 集料的抛光试验

选取云南寻甸县石灰岩(碱性石料)、贵州省罗甸县玄武岩(弱碱性偏中性石料)、花岗岩(酸性石料)3种集料(13.2～16 mm)进行抛光试验，各项基本技术指标如表6所示。

为定量分析3种岩性集料在不同磨光程度下破裂面粗糙度的变化情况，使用振动抛光机改变集料表面纹理的细观构造特征，用氧化铝质量分数95%的1000号一级金刚砂作为磨料，制备具有不同破裂面粗糙度的3种岩性粗集料测试试样[14-15]。

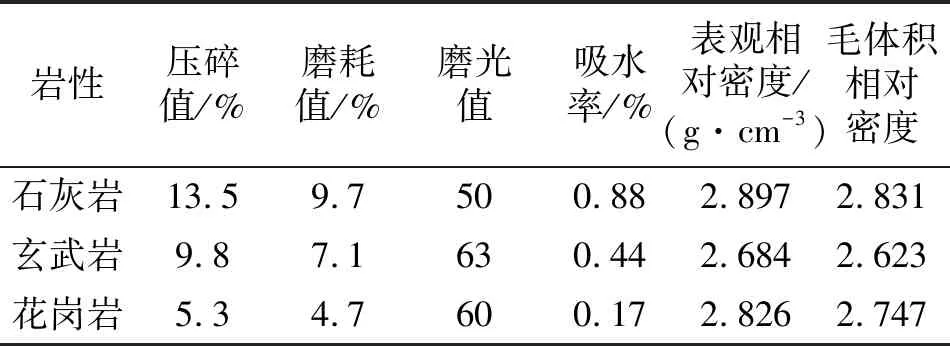
表6 集料的基本性质

3.2 粗糙度评价

分别对具有良好破裂面的10颗石灰岩、10颗玄武岩及10颗花岗岩进行0.5、1.0、1.5、2.0 h不同时间的抛光处理；每段抛光试验结束后，采用间隔30°的6条剖面轮廓线评价方法对集料断裂面表面10 mm×10 mm区域的平均粗糙度系数JRC3D进行评价，计算结果如表7所示。各岩性集料的测试样品在不同抛光时间下测试区域平均粗糙度的变化趋势如图7所示。

表7 集料破裂面平均粗糙度随抛光时间变化

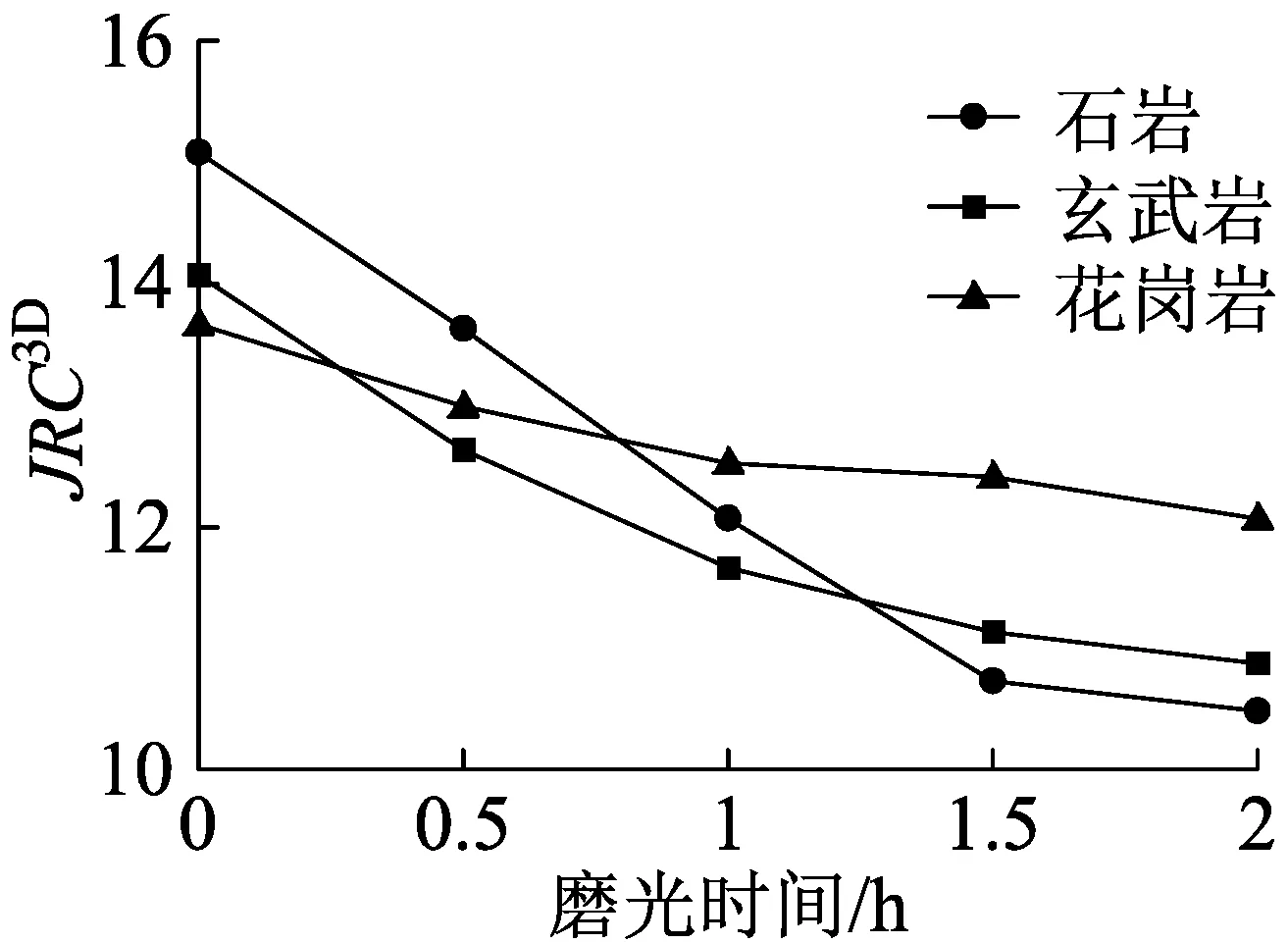
图7 集料破裂面平均粗糙度的变化趋势

试验结果显示，抛光试验前石灰岩集料断裂面表面的粗糙度最高，花岗岩最小，玄武岩居中。随着抛光时间的增加，集料粗糙的纹理表面逐步磨损，表现为不同岩性粗集料表面粗糙度均随磨光时间增加呈下降趋势；其中，石灰岩粗糙度降幅最大，玄武岩次之，花岗岩粗糙度降幅最小，表明玄武岩与花岗岩的耐磨光性能均高于石灰岩，与实际工程中路用集料力学指标的衰减规律一致[15]。综上可见，平均粗糙度系数JRC3D可以较为精确地定量评价集料颗粒表面的粗糙纹理特征，在表征集料三维轮廓面局部区域形貌特征变化时具有良好的敏感性。因此，平均粗糙度系数JRC3D可以作为评价路用集料表面粗糙度的评价指标。

4 结语

为定量描述集料表面的粗糙程度，本文采用轮廓形状分析系统测量集料的表面形态，使用粗糙度系数JRC作为评价指标，研究了集料表面粗糙度的评价方法，获得主要结论如下：

(1)Barton标准剖面法可以定性评价粗集料表面纹理在特定剖面的二维粗糙度特征，但存在人为估值的主观性缺点；表面起伏特征参数法虽可定量表征集料表面的二维剖面粗糙度，但轮廓线的获取对仪器精度要求较高，测量工作量大，评价效率有限；迹线长度表征法中的特征参量指代明确，便于测量与统计，适合在实际工程中用于评价集料表面二维剖面的轮廓线粗糙度。

(2)集料表面粗糙度存在明显的各向异性特征，纹理二维剖面轮廓线粗糙度系数不能全面表征集料三维轮廓面的复杂形态，可将多角度二维剖面轮廓线粗糙度扩展为三维平均粗糙度系数进行定量评价集料表面观测区域内的平均粗糙度特征。

(3)选取平均粗糙度系数JRC3D作为评价指标，可以准确描述集料在不同抛光程度下表面粗糙度的变化情况，具有良好的敏感性，可作为表征路用集料表面粗糙度的评价指标。