建立计算机模型探索颅底凹陷导致寰枢椎脱位的力学机制的研究

首都医科大学 生物医学工程学院（临床生物力学应用基础研究北京市重点实验室），北京 100069

引言

寰枢椎脱位（Atlanto-Axial Dislocation，AAD）是常见的脊柱外科疾病，先天性畸形或发育异常会导致C1和C2脱位或不稳定，有可能压迫到高位颈髓并累及椎-基底动脉。颅颈区的结构相互作用，一旦寰枢椎出现异常，也会导致其他结构异常，其中颅底凹陷最为常见。在颅颈区发育异常或畸形的同时，枕骨会更趋于扁平并且有向内翻折的趋势。变形后的枕骨无法承担颅底骨、寰枢关节、齿状突等结构的压力，进而使得颅底骨向中间凹陷进入颅腔，寰枢关节和齿状突也会呈现向颅底陷入的趋势，从而使脑干和延髓受到压迫，最终引发各种神经脊髓综合征[1]。

对于颅底凹陷引起的AAD，其外科治疗方式一直在不断改善，但目前见报道的完全复位率为75%，仍有部分患者无法完全复位。这是因为当颅底凹陷患者的枢椎侧方关节和齿状突畸形更为严重时，最终使得AAD的力学体制也更加复杂，加重复位的难度。因此，想要制定更为有效的外科治疗方式，就必须要深入研究颅底凹陷和AAD之间的力学机制。目前国内外的相关研究聚焦两个方面：

（1）侧方关节畸形与脱位之间的关系。颅底凹陷患者的颅颈区畸形中，寰枕融合最为常见。如果寰椎侧块和枕髁融合，会导致寰椎侧块失去高度，并且会使得枢椎齿状突向上凹陷进入枕骨大孔，最终导致颅底凹陷。寰椎侧块结合枕髁会形成复合体，复合体在枢椎上关节面会与之构成寰枢椎侧方关节，异常关节面往往在矢状面向前下倾斜，使齿状突向后脱位[2-5]。相关学者的研究和测量均证实侧方关节畸形程度与寰齿关节脱位程度呈正相关[2,6]，还有研究提出侧方关节畸形引起AAD的假说，侧方关节的畸形在矢状面内令颅骨和颈椎失稳，颅骨前移重心和颈椎前凸增加，使得齿状突向后脱位[7]。

（2）齿状突畸形与脱位之间的关系。在寰枢椎结构中，齿横关节对维持寰枢椎矢状面内稳定性有至关重要的作用，而齿状突畸形，横韧带异常都会使得齿横关节失稳，从而导致AAD[8-11]。颅底凹陷患者在颅颈区出现畸形的同时，侧方关节和齿状突结构也会受到累及而发育异常或出现畸形。因此颅底凹陷和AAD之间的作用机制，不仅与寰枢椎侧方关节畸形有关，也与枢椎齿状突畸形有密切关系。

先天性颅底凹陷病人因复杂的三维畸形病理特点使得常规生物力学模型、物理模型、在体模型等均无法用于研究[12]，计算机模型则提供了新的思路，只需采集病人的CT图像并借助图像处理软件的重建算法，即可得到颈椎三维几何模型。本研究将分别建立正常人、颅底凹陷不合并AAD患者、颅底凹陷合并AAD患者的三维几何模型，讨论侧方关节畸形和齿状突畸形与AAD之间的关系，探索颅底凹陷导致AAD的力学机制，以利于优化外科手术的方案。

1 材料与方法

1.1 样本

采用20位无既往颈椎病史的成年志愿者的颈椎CT断层图像、20位颅底凹陷不合并AAD的患者的颈椎CT断层图像、20位颅底凹陷合并AAD的患者的颈椎CT断层图像来完成建模，采集数据使用西门子SOMATOM Sensation 64/Cardiac 64螺旋CT机，扫描层距为0.6 mm，临床图像资料以512×512像素的DICOM格式保存数据。

1.2 三维几何模型构建

1.2.1 软硬件配置

本研究所建立模型的硬件配置采用Hasee Computer N8xEJEK(CPUi5-8300h，内存8192 MB RAM，硬盘250 G）。本研究使用Mimics Research 20.0、IBM SPSS Statistics 21软件完成。

1.2.2 颈椎三维几何模型构建方法

通过CT图像灰度特征来设定不同的阈值特性，之后基于空间连接性演算，利用确定好的CT阈值范围，在某一横截面选择种子点，再通过编码和运算，找寻临近与之连接的演算点（像素点）。通过不断的编码和运算，最终整个阈值范围的像素点都被选取成为蒙版，将蒙版内相邻像素连接即可获得颈椎三维几何模型。如图1所示，分别为正常对照志愿者、颅底凹陷不伴有AAD患者、颅底凹陷伴有AAD患者的颈椎三维几何模型。

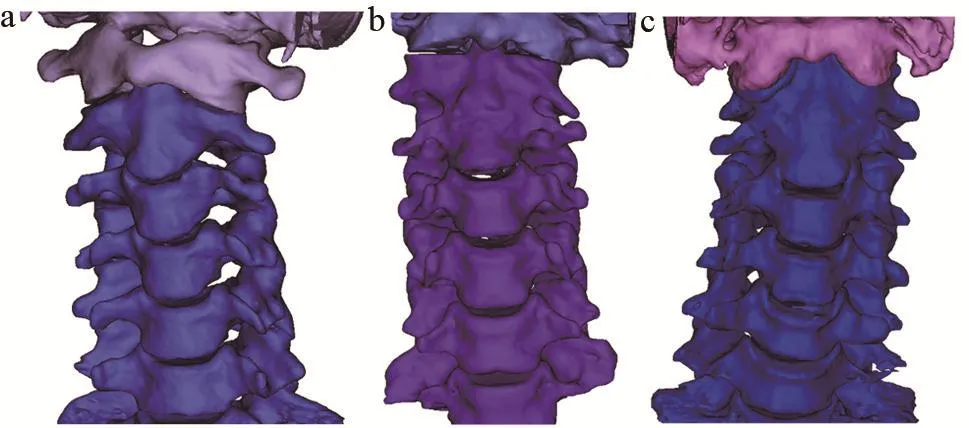
图1 颈椎三维几何模型

1.3 形态学参数评价指标

1.3.1 颅底凹陷程度

钱氏（Chamberlain）线，硬腭后缘与枕骨大孔后缘间的连线，亦称腭枕线。正常人齿状突在此线的3 mm以下，若超过此限，即为颅底凹陷症。本研究采用在矢状位图像中齿状突尖部距钱氏线距离判断颅底凹陷的程度，在颈椎矢状位图像中通过测量颅骨斜坡前缘和齿状突前边界之间的夹角获得颅颈倾角辅助分析颅底凹陷[13-14]。

1.3.2 AAD程度

齿状突与寰椎两侧块之间的距离不对称，两侧块与枢椎体关节不对称或一侧关节间隙消失或重叠是脱位的征象。寰椎前弓与齿状突前面的距离正常人不超过2.5 mm，若超过此范围即为前脱位。在横截面图像中测量齿突前正中点到寰椎前弓后缘的距离，即寰齿前间距（Atlanto Distance Interval，ADI），用来判断AAD 程度[15-16]。

1.3.3 齿状突畸形参数

设定一组参数（齿状突高度、齿状突高度与齿状突基底宽度的比值、齿状突倾斜角度）作为表征齿状突畸形的形态参数。在建立好的颈椎模型上，利用齿状突两侧与枢椎椎体移行的位置为齿状突基底的两端，连线两个端点作为齿状突的基底线，测量齿状突基底线的长度得到齿状突基底宽度D，通过测量齿状突尖部距齿状突基底线的垂直距离即可得到齿状突高度H，测量齿状突两个倾角θ1和θ2及倾角差值来研究齿状突不规则倾斜程度。利用齿状突高度、齿状突高度/齿状突基底宽度和齿状突倾角评价齿状突畸形形态如图2所示。

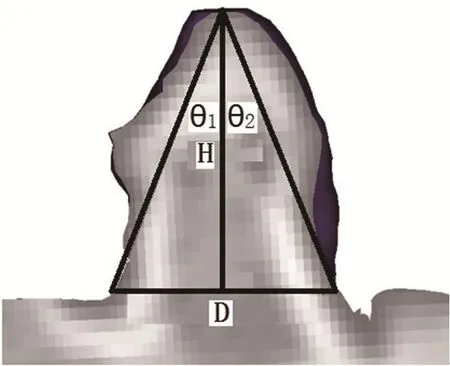
图2 齿状突畸形参数示意图

1.3.4 侧方关节畸形参数

本文选用颅颈倾角和矢状面夹角作为表征侧方关节畸形的形态参数[13-14]，在颈椎矢状位图像中，齿状突前缘和颅骨斜坡前缘之间所呈夹角即颅颈倾角，利用齿状突后边界作为辅助线，记录与枢椎上关节面水平面的夹角即可测量左右两个矢状关节面夹角。

1.4 统计学分析

本研究利用IBM SPSS 21软件进行统计学分析，选用的样本满足独立性，需进行检验正态性和方差齐性。对所有参数进行正态性和方差齐性检验分析，由于每组样本数为20<50，故采用Shapiro-Wilk法，每组正态性检验值均大于0.20时可以认为样本来自正态总体。齿状突尖部距Chamberlain线距离、齿状突高度/基底宽度和矢状位关节倾角来自正态总体，而ADI、齿状突高度、齿状突基底宽度、齿状突倾角θ1、齿状突倾角θ2、齿状突倾角差值、颅颈倾角并非来自正态总体。利用Levene方差齐性检验方法，当数据基于均值的P＞0.10时可认为数据具有方差齐性。则可知齿状突高度、齿状突基底宽度具有方差齐性。而齿状突尖部距Chamberlain线距离、ADI、齿状突高度/基底宽度、齿状突倾角θ1、齿状突倾角θ2、齿状突倾角差值、矢状位关节倾角、颅颈倾角不具有方差齐性。经过以上的检验，每组数据均不同时满足方差分析和最小有意义LSD-t检验的使用条件。

根据正态性检验和方差齐性检验的理论，如果样本不满足正态性与方差齐性，则需采用非参数检验方法，非参数检验是不依赖特定的总体分布，也不对总体参数进行推断的一类统计分析方法，又称任意分布检验。用于比较多个独立样本的非参数检验方法是在Wilcoxon秩和检验基础上扩展而来的Kruskal-Wallis检验，可用于比较多个总体的分布位置是否相同。采用Kruskal Wallis检验分析整体数据，原假设为各总体差异分布情况相同，选用独立样本Kruskal Wallis检验，齿状突尖部距Chamberlain线距离、ADI、齿状突高度、齿状突高度/基底宽度、齿状突倾角θ1、齿状突倾角θ2、矢状位关节倾角、颅颈倾角P＜0.001，拒绝原假设。齿状突尖部距Chamberlain线距离、ADI、齿状突高度、齿状突高度/基底宽度、齿状突倾角θ1、齿状突倾角θ2、矢状位关节倾角、颅颈倾角在α=0.05的检验水平下差异有统计学意义，可认为三组的数据不全相等，而齿状突基底宽度、齿状突倾角差值差异无统计学意义。

多个独立样本经过Kruskal-Wallis检验拒绝H0时，认为各总体的分布位置不全相同，还需进行组间多重比较来推断某两个总体的分布位置是否不同，如采用Bonferroni校正的近似正态Z检验组间差异[17]。

Spearman秩相关系数是一个非参数性质（与分布无关）的统计参数，用来度量两个变量之间联系的强弱，通常被认为是排列后变量之间的Pearson线性相关系数。

2 结果

2.1 颅底凹陷程度

对齿状突尖部距Chamberlain线距离，得到不脱位组、脱位组与正常组比较差异均有统计学意义（P＜0.001），不脱位组和脱位组之间比较差异无统计学意义（P＞0.999）（表1）。

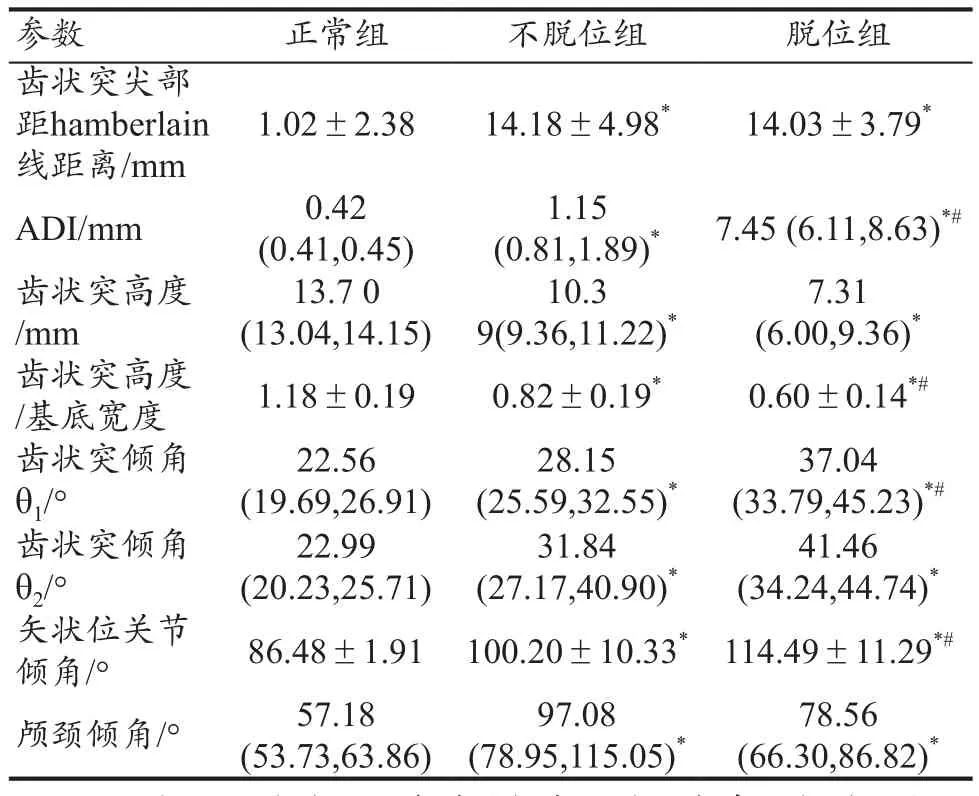
表1 各项参数检测结果

2.2 AAD程度

对ADI进行分析后，三组间任意两组间差异具有统计学意义（P＜0.05）。

2.3 齿状突畸形参数

对齿状突高度进行分析后，得到不脱位组、脱位两组与正常组比较差异均具有统计学意义（P＜0.001），不脱位组和脱位组之间比较差异无统计学意义（P=0.054＞0.05）。对齿状突高度/基底宽度进行分析，三组间任意两组间差异具有统计学意义（P＜0.05）。对齿状突倾角θ1进行分析，三组间任意两组间差异具有统计学意义（P＜0.05）。对齿状突倾角θ2分析后，得到不脱位组，脱位两组与正常组比较差异均具有统计学意义（P＜0.001），不脱位组和脱位组之间比较无统计学意义（P=0.114＞0.05）（表1）。

2.4 侧方关节畸形参数

对矢状位关节倾角进行分析，三组间任意两组间差异具有统计学意义（P＜0.05）。对颅颈倾角进行分析后，不脱位、脱位两组与正常组比较差异具有统计学意义（P＜0.001），不脱位组和脱位组之间比较差异不具有统计学意义（P=0.066＞0.05）（表 1）。

2.5 相关性分析

以矢状位关节倾角作为表征侧方关节畸形的参数，计算齿状突参数与侧方关节畸形的相关性（表2）。从结果中可以看出，齿状突高度、齿状突高度/基底宽度与侧方关节畸形显著负相关，其他两个参数与侧方关节畸形显著正相关。

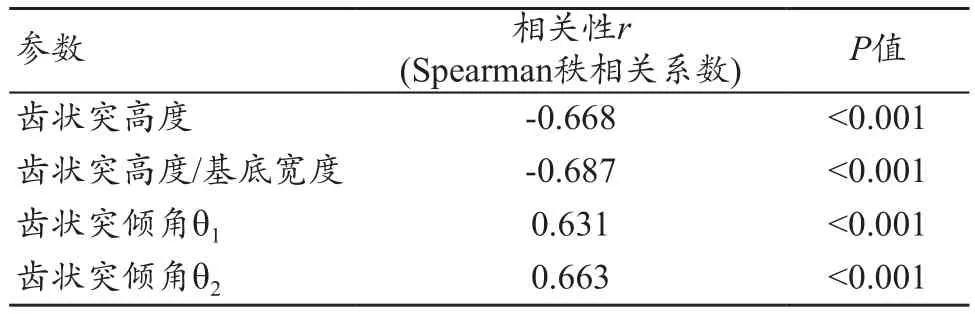
表2 相关参数与侧方关节畸形之间的相关性

以齿状突尖部距Chamberlain线距离作为颅底凹陷程度的参数，计算参数与颅底凹陷之间的相关性（表3），从结果中可以看出，齿状突高度、齿状突高度/基底宽度与颅底凹陷显著负相关，其他四个参数与颅底凹陷显著正相关。

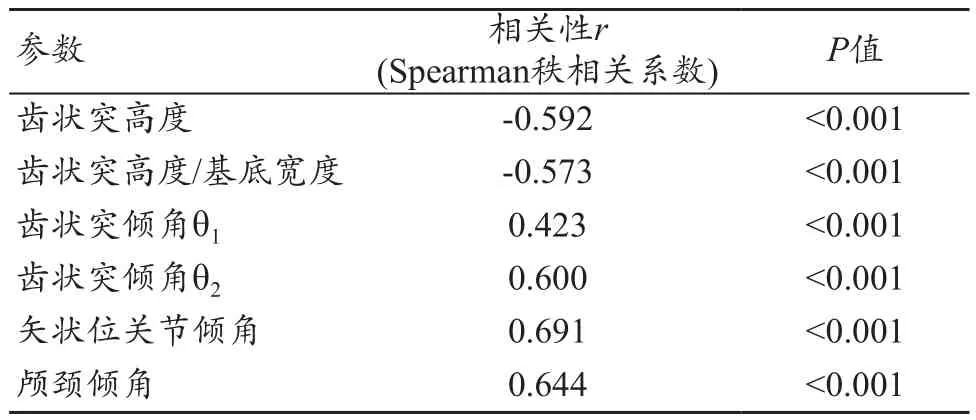
表3 相关参数与颅底凹陷之间的相关性

以ADI作为AAD程度的参数，计算参数与AAD之间的相关性（表4），从结果中可以看出，齿状突高度、齿状突高度/基底宽度与AAD显著负相关，其他四个参数与AAD显著正相关。

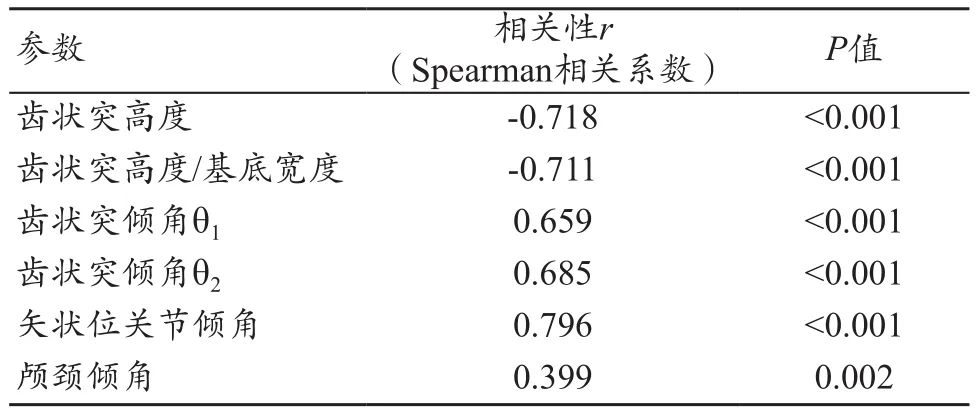
表4 相关参数与AAD之间的相关性

3 讨论

寰枢椎关节是人体活动最大的关节，其周围有寰椎前弓、十字韧带限制活动并维持稳定，其旋转和移动则受到翼状韧带的限制，这些结构的损伤或变形将会影响到寰枢椎关节的稳定性。许多研究表明颅底凹陷患者侧方关节畸形和AAD之间有显著的相关性，因此颅底凹陷患者侧方关节畸形是导致AAD的重要原因。颅底凹陷不仅导致侧方关节畸形，也会使齿状突发生不同程度的畸形，有学者认为颅底凹陷患者的齿状突畸形作为颅底凹陷患者重要的病理学特征，与颅底凹陷导致AAD的发生机制有很密切的关系[18-20]。

本研究从前人的研究基础出发，探究侧方关节畸形和齿状突畸形与颅底凹陷导致AAD之间的关系。创新点之一是在建立的不同组别的颈椎三维模型上对各类参数进行测量，相比较二维的图像可以更精确地选取测量点，以便提高测量精度。创新点之二是在测量齿状突高度和基底宽度的同时增加两个表征齿状突倾斜角度的参数，这些参数在统计学分析后均表明差异具有统计学意义。

本研究发现齿状突的两个形态参数（齿状突高度、齿状突高度/基底宽度）与枢椎上关节面的形态参数（矢状位关节倾角）具有显著的负相关性，说明颅底凹陷患者齿状突高度丢失很可能与上关节面畸形有关。证明颅底凹陷引起侧方关节畸形同时，亦会导致齿状突畸形，侧方关节畸形越严重，齿状突高度丢失越严重。齿状突趋向扁平与椎体融合，令横韧带很难限制其在矢状面的活动。同时在矢状面也会令寰枢椎失去稳定性，导致AAD。齿状突高度和齿状突高度/基底宽度与颅底凹陷亦存在显著相关性，即颅底凹陷越严重，齿状突的高度越低，齿状突的形态越倾向于扁平。颅底凹陷越严重的患者，枢椎齿状突对延髓和颈髓压迫的越严重，齿状突高度丢失，形态变得扁平可以减轻对延髓和脊髓的压迫，这可能是为了避免加重神经结构压迫的一种代偿性的改变，与Xia等[16]研究得到的结果相符。

本研究创新点所涉及的齿状突两个倾角也符合上述的特点，其与枢椎上关节面的形态参数（矢状位关节倾角）、颅底凹陷均存在显著相关性，从形状角度上也可以看出颅底凹陷越严重会导致齿状突越扁平，两个倾角越大，同时也会反映出侧方关节畸形越严重。而倾角差值参数却没有统计学意义，可能因为倾角从最高点选取，不能完全地表现齿状突的畸形倾斜程度，且样本量较少，也许选用更多的样本能探究出齿状突畸形倾斜与颅底凹陷程度之间的关系。

脱位组的齿状突高度仅与正常人组相比差异具有统计学意义，而与不脱位组相比差异不具有统计学意义，这与相关研究结果[16]不同。同时，齿状突高度/基底宽度与两组相比差异均具有统计学意义，若排除测量误差和统计学方法不同造成的差异，这是否可以说明齿状突代偿性趋向扁平时，齿状突宽度宽而齿状突高度变化更小，而齿状突宽度数据不具有统计学意义，也许齿状突宽度更宽而高度变化小只是特例，这里只是提供一种可能的猜想。齿状突倾角θ1与两组相比差异均具有统计学意义，齿状突倾角θ2与正常人组差异有统计学意义，而其与不脱位组差异没有统计学意义，这说明这两个新设定的角度参数对颅底凹陷、AAD患者的相关性分析有一定参考意义。

4 结论

本项研究建立三维模型并进行形态学测量，选定了与齿状突畸形相关的四个参数表征颅底凹陷患者齿状突畸形的程度，其中，齿状突的两个倾角辅助证明齿状突畸形更加趋向扁平。分析侧方关节、齿状突畸形、颅底凹陷和AAD间的关系，发现侧方关节畸形和枢椎齿状突畸形是颅底凹陷患者出现AAD的重要原因。