基于GUM 法评定一般压力表示值误差测量结果不确定度的研究

冯鹏军

（天水市秦安县质量技术监督检测所，甘肃 天水741600）

在实际工作中，测量结果的不确定度我们用概率密度函数来表示。评定方法根据JJF1059 进行，此规范分为两部分：第一部分为JJF1059.1-2012《测量不确定度评定与表示》，第二部分为JJF1059.2-2012《用蒙特卡洛法评定测量不确定度》，我们把第一部分又称GUM 评定方法，第二部分称MCM 评定法。在计量检定工作中，对测量不确定度的评定一般选用GUM 法，此次评定将以1.6 级普通压力表为检定对象，用GUM 法分别评定A类、B 类、人员读数、机械元件、环境五方面的不确定度分量，最终以拓展不确定度表示。

1 测量基本条件及依据

1.1 测量依据

依据JJF1059.1-2012 《测量不确定度评定与表示》；JJG52-2013《弹性元件式一般压力表、压力真空表和真空表计量检定规程》。

1.2 检定环境

此次检定我们在温度为21℃、相对湿度50%的压力实验室进行，检定开始前，先将检定合格的0.4 级精密压力表和1.6 级一般压力表在压力实验室静置2 小时，然后按照检定规程要求用比较法测量。

1.3 测量方法

选用手动液压源，通过升压检定和降压倒序反检两个程序，将1.6 级压力表的各检定点与0.4 级精密压力表各点直接进行比较，轻敲读取被检表各检定点示值，此时1.6 级压力表的示值与0.4 级精密压力表示值之差即为1.6 级压力表的示值的误差。

1.4 数学模型

δ=P被－P标

P被-被检表在被测点上的示值；

P标-标准表示值。

2 标准不确定度分量评定

2.1 标准不确定度分量评定

A 类不确定度分量评定：

用本装置对1.6 级压力表1Mpa 处进行10 次重量测量，得到下列数据：

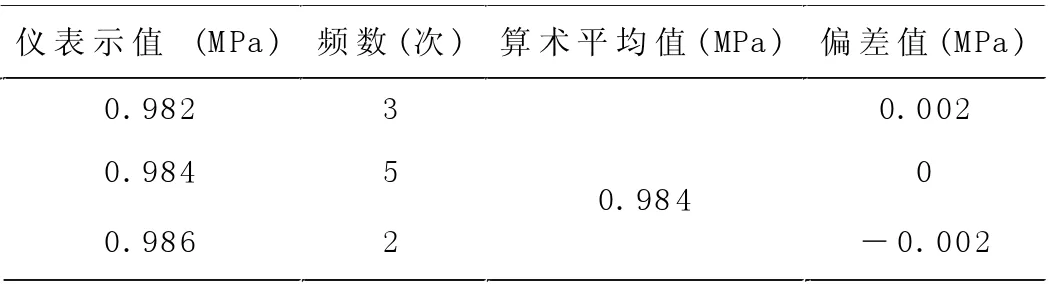
表1

依据贝塞尔公式，1.6 级压力表算术平均值的实验标准偏差为：

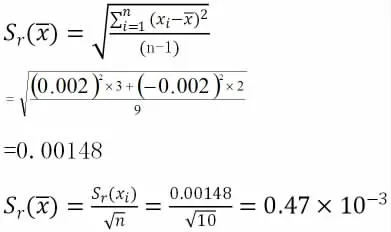
A 类 不 确 定 分 量 U1=Sr（x）=0.47 ×10-3， 自 由 度V1=n-1=10-1=9

B 类不确定度分量的评定：

表2 标准不确定度一览表

元件弹性后滞引进不确定度评定：

2.2 合成标准不确定度。见表2。

合成标准不确定度计算：

因上述不确定度分量相互独立，因此：

2.3 扩展不确定度

置信概率我们取P=95%，按算得的有效自由度大于100，查分布表得到k=1.96，则扩展不确定度：

U=KUc=1.96×3.86×10-3=0.76×10-2

2.4 测量不确定度报告

1.6 级弹性原件式压力表在温度21℃、相对湿度50%的大气压下的测量结果扩展不确定度为:

U=0.76×10-2（P=95%）

3 结论

此次示值误差测量结果不确定度的评定，我们仅选取了A类、B 类、人员读数、机械元件和环境5 方面的分量进行评定，而在不同地区、不同时段的大气压也有一定的差别，也会影响检定结果的不确定度。由此可见，不确定度的引入也有一定的不确定性，所以检定结果报告只能以置信概率的方式报告。当检定结果的可信赖程度用不确定度表示时，越小则表明的结果越接近真值，反之则表明越远离真值。所以，我们在出具检定报告时都会给出不确定度，以便使用者对结果的可靠性进行评定。