基于马尔可夫链的飞行器任意线束线间串扰预测方法

包贵浩 蔡志勇 黄凌龙 石 磊

（中航通飞华南飞机工业有限公司，广东 珠海519040）

飞行器的实际电路和布线中，线缆布局会随着外形的变化而改变走向，非平行传输线的情况是不可避免的。任意布局线束会导致传输线分布参数的不确定性，从而影响传输线线间串扰和受高强辐射场（HIRF）干扰的预测。

1993 年，S. Shiran、B. Reiser 等提出了蒙特卡洛算法[1]，1999年，S. Salio、F. Canavero 等提出随机中点位移（Random Midpoint Displacement，RMD）算法[2]。上述两种算法都可以反映出任意线束中传输线径向位置随机分布的特征，但子段节点模型间会出现非线性不连续问题，导致两种算法均不能有效地建立一条连续逼真的任意线束模型。2007 年，S. Sun、G. Liu、J. Drewniak 等提出了随机位移曲线插值（the Random Displacement Spline Interpolation，RDSI）算法[3]，相比较RMD 算法，RDSI 算法使子段节点模型具有较好的线性连续性，线束内传输线沿径向平滑变化，比较符合非平行传输线的径向位置分布特点。随后，Diego Bellan、Sergio A. Pignari 等提出了编帘法（Lacing Cords）[4]来分析任意线束串扰的统计特性。Meilin Wu、Daryl G. Beetner 等还提出了合理最坏情况估计法（Reasonable Worst-Case）[5]，该方法有效地减少统计分析庞大的计算量，但会带来串扰预测的过估计问题。

本文应用马尔可夫链的特征，提出一种新的任意布局线束模型，并通过仿真验证表明马尔可夫链模型应用于任意布局线束线间串扰预测的有效性。

1 马尔可夫链

马尔可夫链概率分布最重要的参数为条件概率P{ξ（n+1）=j|ξ（n）=i}，也称之为在时刻n 时的一步转移概率Pij（n），表示在时刻n 时ξ（n）取i 值的条件下，在下一时刻n+1 时ξ（n+1）取j 值的概率。一步转移概率Pij（n）具有两个性质：

若在马尔可夫链中P{ξ（n+1）=j|ξ（n）=i}=Pij，即从i 状态转移到j 状态的概率与n 无关，则该类马尔可夫链称为齐次马尔可夫链。

令P 为一步转移概率Pij所组成的转移概率矩阵，状态空间为Ω≡{0，1，…，K}，则P 可以表示为

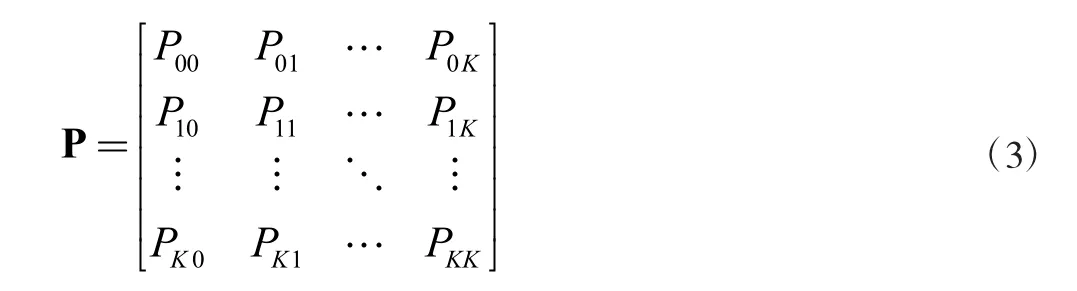
2 任意布局线束模型

任意布局线束中传输线的径向位置分布具有随机性，沿线束径向将长度为l 的传输线分割成N 段等长节点，则该N 段等长节点径向位置的集合可以看作为一个离散随机过程。任意布局线束中传输线的径向走线和截面位置，如图1 所示。传输线的截面位置坐标用二维变量（xi，yi）来表示，全部截面位置坐标{（x1，y1），…，（xi，yi），…，（xM，yM）}即为该离散随机过程的状态空间D。

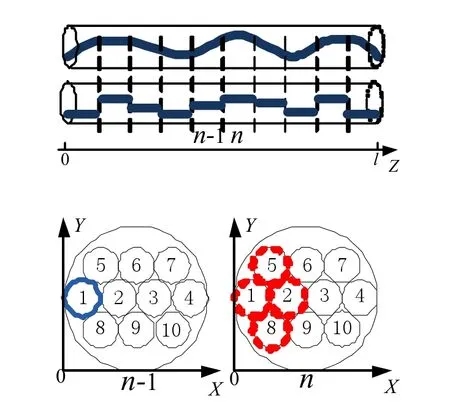
图1 任意布局线束的径向走线和截面位置示意图

通过传输线径向走线特征的分析，可以合理假设传输线第n 段节点的截面位置仅与第n-1 段节点的截面位置有关。以图1 所描述的10 芯线束为例，假设第n-1 段节点的位置坐标为（x1，y1），受上一段节点影响，第n 段节点的位置坐标极有可能为其相邻或相同的坐标（x1，y1）、（x2，y2）、（x5，y5）或（x8，y8），且n=2，…，10 均成立。

任意布局线束传输线的径向走线特征具有齐次马尔可夫链的性质，N 段等长节点截面位置的集合可以抽象为齐次马尔可夫链{T（n），n = 1，2，…，N}，其状态空间为D≡{（x1，y1），（x2，y2），…，（xM，yM）}，M 为线束个数。线束内节点截面位置的状态转移概率矩阵P 可以表示为

其中，状态转移概率Pij表示上段节点的位置坐标为（xi，yi）时，本段节点的位置坐标为（xj，yj）的概率，Pij的大小与两个位置坐标（xi，yi）和（xj，yj）的相对距离Δij有关，可以用幂级数表示为

其中，相对距离Δij的计算公式为

线束的传输线个数决定了幂级数表达式的阶数。以10 芯线束为例，状态转移概率Pij与相对距离Δij的关系可以近似表示为

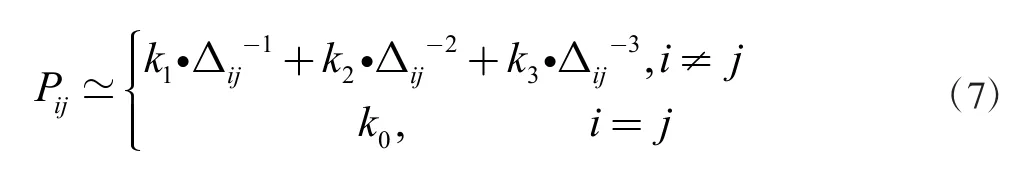
其中，k0、k1、k2、k3为幂级数系数，采用下式计算求解

在线束初始节点位置已知的情况下，通过状态转移矩阵P可以逐级地求解得到后续各节点可能的位置坐标，进而建立起任意布局线束模型。

本文利用Matlab 仿真实现基于RDSI 算法和齐次马尔可夫链算法的任意线缆束模型，如图2 所示。相比较RDSI 模型可以看出，齐次马尔可夫链模型同样可以很好地优化线束节点间的连续性，较真实地逼近非平行传输线。

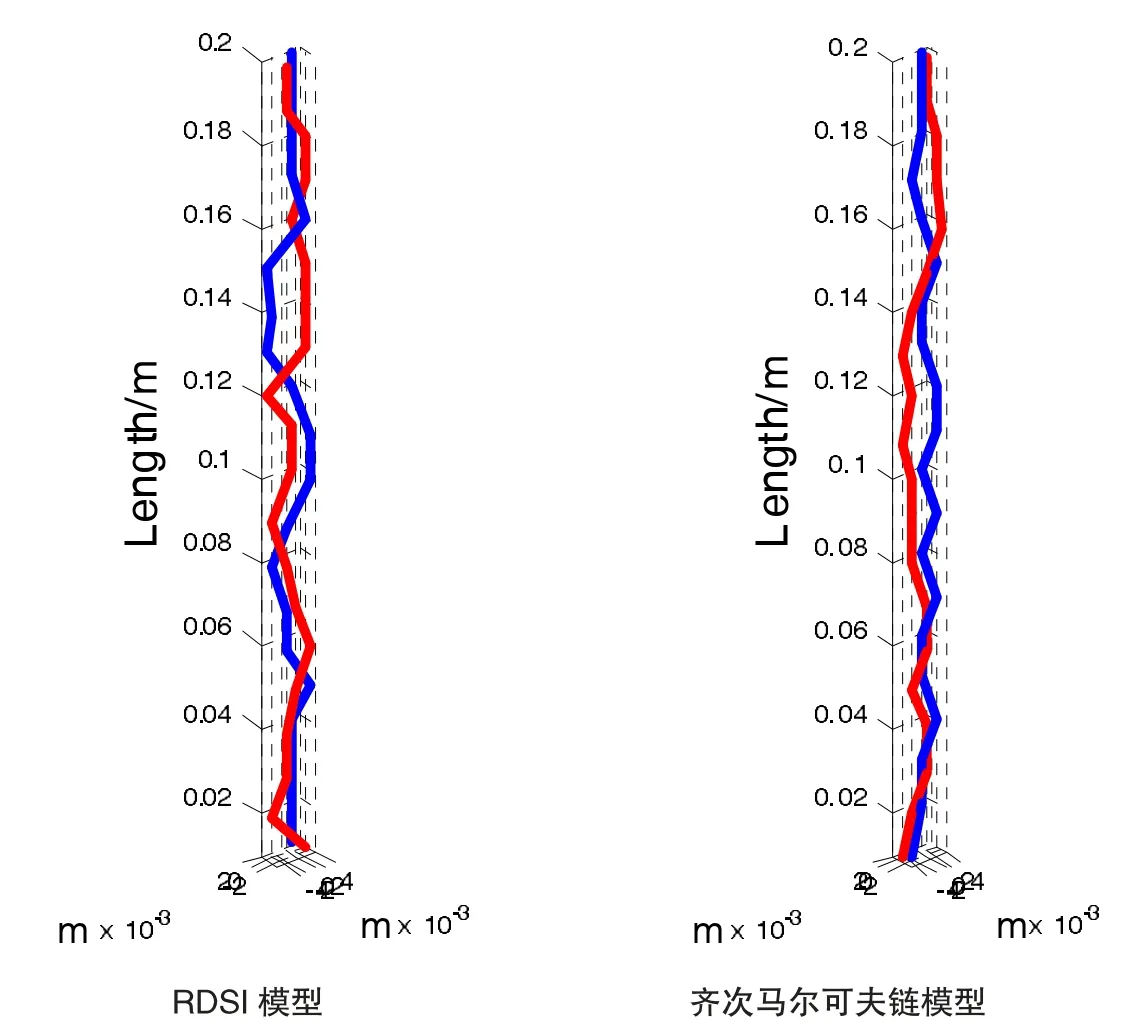
图2 任意线缆束模型

3 线间串扰的仿真验证

以10 芯线束作为仿真实例，分别以RDSI 算法和齐次马尔可夫链算法仿真计算发射导线和接收导线间的串扰。仿真设置如下：假设10 芯线束的长度为l=0.6m，线束轴心距离地平面的高度为h=2×10-2m，导线的实芯半径为r=1×10-3m，绝缘层半径为R=2×10-3m，导线间的间距为d=2R，如图3 所示。令导线#1为发射导体，其电压源VS的电压幅值为1V，内阻为RS，发射导体的负载为RL，导线#2 为接收导体，端接电阻分别为RNE和RFE，如图4 所示。

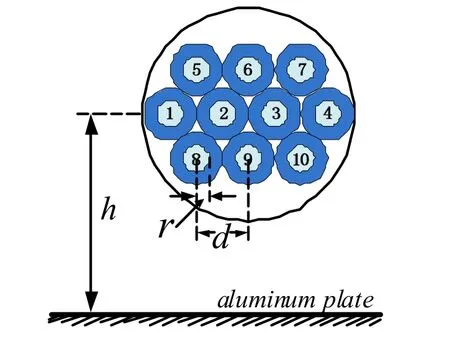
图3 10 芯线束的截面位置关系图

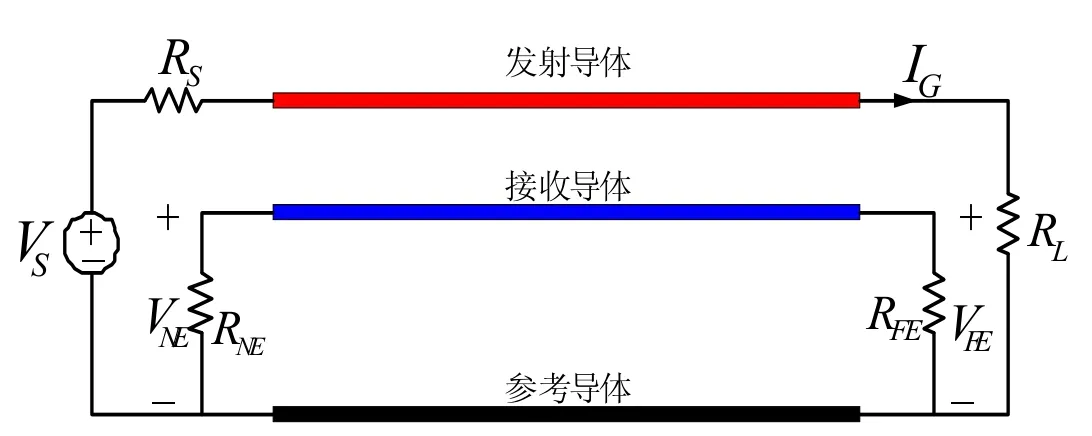
图4 发射和接收导线的电路图

仿真频率范围为1kHz～100MHz，针对RS=RL=RNE=RFE=50Ω，进行50 次仿真，仿真结果如图5 所示，红实线为齐次马尔可夫链模型的任意线束近端串扰仿真曲线，蓝虚线为RDSI 模型的仿真曲线。

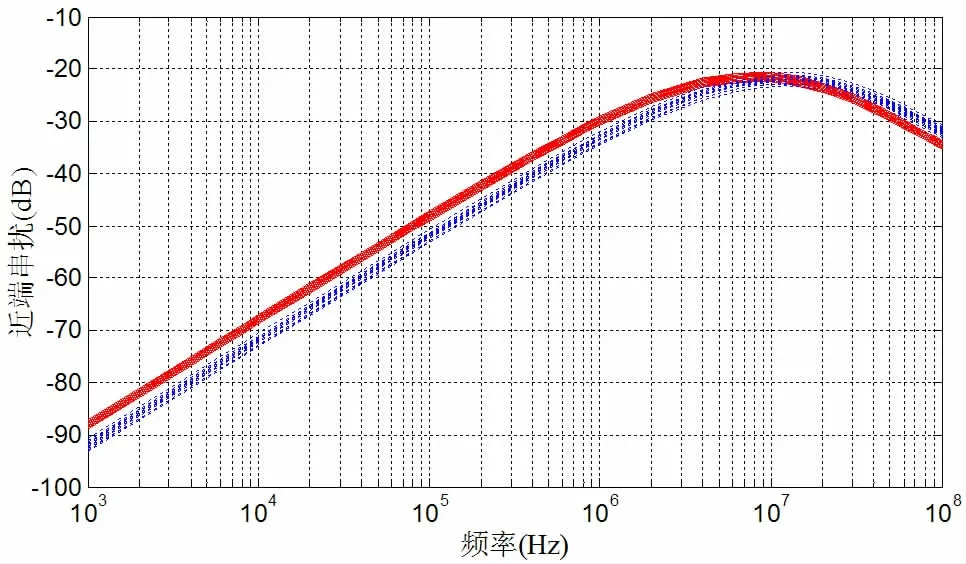
图5 RS=RL=RNE=RFE=50Ω 时接收导线的近端串扰

两种模型的仿真曲线基本吻合，齐次马尔可夫链模型可用于任意线束线间串扰的统计特性分析，其近端串扰仿真结果与RDSI 模型的仿真结果相比高3 ～4dB，对飞行器布线电磁兼容性设计要求更为严格，对实现飞行器的电磁兼容性设计更为有利。

4 结论

本文利用马尔可夫链描述任意线束内非平行传输线径向分布的随机性，将线束分割为N 段，建立任意线束的齐次马尔可夫链模型，并与成熟的RDSI 模型比较具有较高的一致性。通过线束建模仿真验证，齐次马尔可夫链模型的线间串扰仿真收敛性较好，仿真结果与RDSI 模型的仿真结果基本吻合，可用于任意线束线间串扰的统计特性分析。