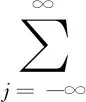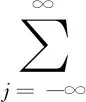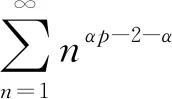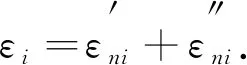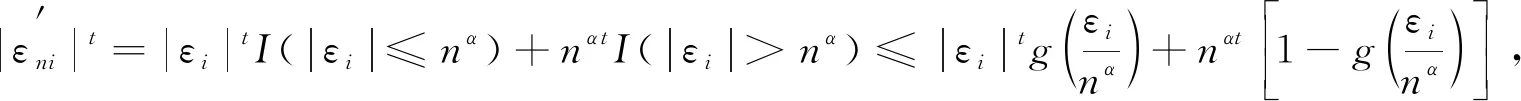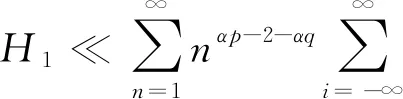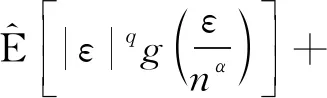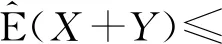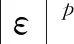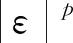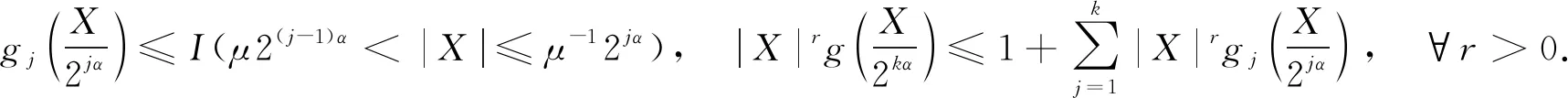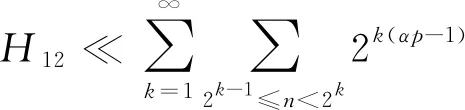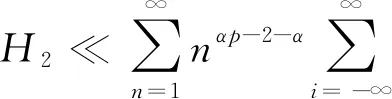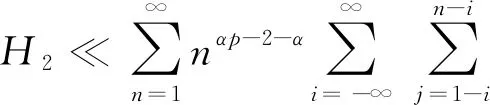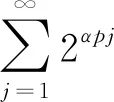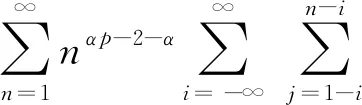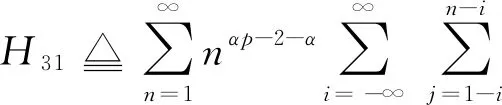次线性期望下具有随机系数相依线性过程的完全积分收敛性

张冰冰,吴群英

(桂林理工大学 理学院,广西 桂林 541004)

1 引言与预备知识

极限理论广泛应用于金融和统计等领域. 传统概率极限理论主要处理模型确定或近似确定的情形,但在实际应用中模型通常是不确定或近似确定的,导致大量信息和数据在概率空间下处理受限. 针对该问题,Peng[1-3]提出了次线性期望空间的理论体系. 目前,关于次线性空间理论的研究已得到广泛关注: Chen[4]得到了次线性期望下独立同分布随机变量序列的强大数定律; Zhang[5]将随机变量的范围进一步扩大得到次线性期望下ND(negatively dependent)序列的Kolmogorov强大数定律; Zhang[6-7]给出了一系列的重要不等式,为研究次线性期望空间下的极限理论提供了有力工具.

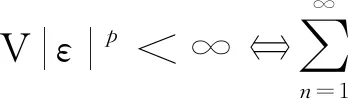
线性过程在经济、金融数学、工程、物理学等领域,特别是在时间序列分析中具有重要作用. 令{εn,n∈}是独立同分布的随机变量序列,{an,n∈}是实数序列,则称为线性过程(或移动平均过程). Phillips等[8]研究了线性过程的渐近性; Ko[9]得到了在Hilbert空间下线性过程的强大数定律; Li等[10]研究了线性过程的完全收敛性; Hosseini等[11]得到了具有随机系数的相依线性过程的完全矩收敛；Chow[12]首次引入了完全矩收敛的概念，完全矩收敛比完全收敛更精确; Wu等[13-14]将完全矩收敛推广到NA(negatively associated)和ND随机变量中; Qiu等[15]推广了完全矩收敛,得到了END(extended negatively dependent)序列的完全收敛性. 本文讨论次线性期望空间下的完全积分收敛性,将概率空间下具有随机系数相依线性过程的完全矩收敛推广到次线性空间下.

令(Ω,F )是给定的可测空间,H是定义在(Ω,F )上由实函数构成的线性空间,若X1,…,Xn∈H,则对∀φ∈Cl,Lip(n),有φ(X1,…,Xn)∈H,其中Cl,Lip(n)是局部Lipschitz函数,即存在c>0及仅依赖于φ的m∈,恒有

本文记X∈H.

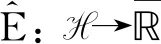
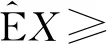
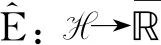
定义2[3]令G⊂F,对函数V: G→[0,1],如果V(Ø)=0,V(Ω)=1,对∀A⊆B,A,B∈G,有V(A)≤V(B),则函数V: G→[0,1]称为容度.

若对所有的A,B∈G,A∪B∈G,均有V(A∪B)≤V(A)+V(B),则称V具有次可加性.

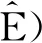
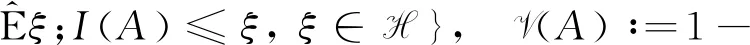
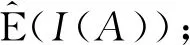
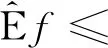
(1)

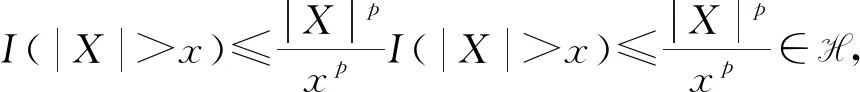
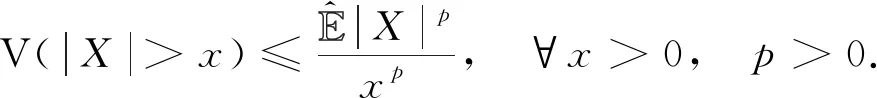
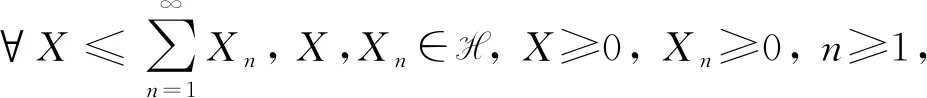
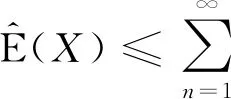
2) 若函数V: F →[0,1]满足

则称函数V: F→[0,1]为可数次可加[3].

定义Choqet积分为

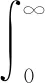
可用V代替 V得到相应的积分.

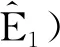
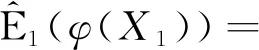
则称X1和X2同分布；若对每个i≥1,X1,Xi都是同分布的,则称随机变量序列{Xn;n≥1}是同分布的.

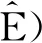
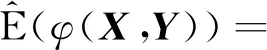
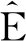
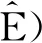
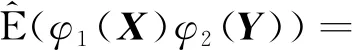
(2)

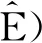
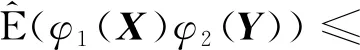
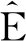
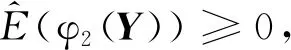
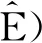
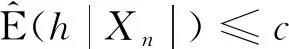
(3)

则称随机变量序列{Xn,n≥1}被随机变量X随机控制.

本文用an≪bn表示存在一个常数c>0,使得当n充分大时,有an≤cbn；I(·)表示示性函数.

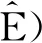
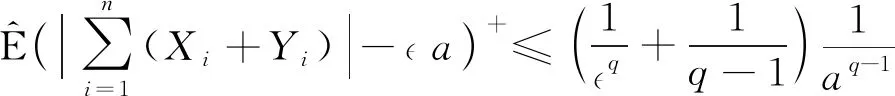
证明: 因为(|a+b|-|c|)+≤(|a|-|c|)++|b|, 所以

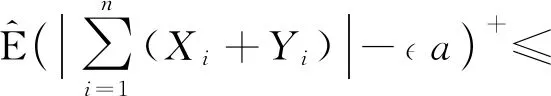
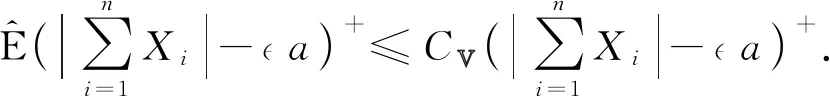
再由q>1和Markov不等式,得

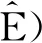
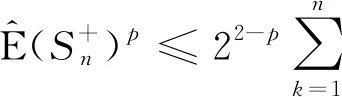
引理3设{εn,n∈}和{An,n∈}是次线性期望空间(Ω,H,下的两个ND随机变量序列,}关于{An,n∈}在下是独立的. 设1≤p≤2,几乎处处收敛,具有可数次可加性,则

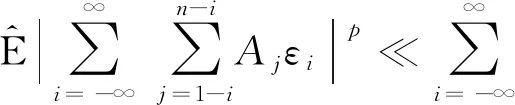
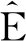
因为{εn,n∈}关于{An,n∈}在下是独立的,所以{εn,n∈}关于n∈}和}在下也是独立的. 再由的次可加性及式(2)和得

从而由引理2,得

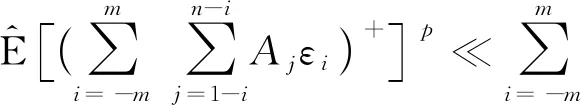
同理有

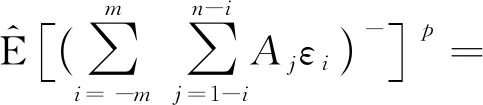
2 主要结果

定理1设{εn,n∈}和{An,n∈}是次线性期望空间(Ω,H,下的两个ND随机变量序列,=}关于{An,n∈}在下是独立的,{εn,n∈}被随机变量ε随机控制,且CV<∞,具有可数次可加性. 对α>0,1

(4)

且对某一p

(5)

(6)

证明: 由于{εn,n∈}是一个ND随机变量序列,为使该序列截尾仍是ND序列,则需要截尾函数非增(非减)并属于Cl,Lip. 令∀c>0,

fc(x)=-cI(x<-c)+xI(|x|≤c)+cI(x>c),

对∀1≤k≤n,n≥1,

则有

(7)

对0<μ<1,设g(x)∈Cl,Lip是一个偶函数,并在x≥0上是单调下降的,使得对∀x∈,0≤g(x)≤1,且当|x|≤μ时,g(x)=1; 当|x|>1,g(x)=0. 则

I(|x|≤μ)≤g(x)≤I(|x|≤1),I(|x|>1)≤1-g(x)≤I(|x|>μ).

(8)

(9)

因此对n≥1,有

从而由引理1得

首先证明H1<∞. 由引理3得

(12)

由Cr不等式和式(3),(9),得

由式(1),(8)得

(14)

于是由式(5),(12)～(14),得

因此对任意的c>0,有

(16)

令a>1,得

(17)

对j≥1,设gj(x)∈Cl,Lip()是一个偶函数,使得对∀x∈,0≤gj(x)≤1,且当2(j-1)α≤|x|≤2jα时,gj(x/2jα)=1; 当|x|≤μ2(j-1)α或|x|>μ-12jα时,gj(x/2jα)=0. 则

(18)

当p>0,2αp>1时,由式(1),(5),(8),(17)得

由式(19)得

(20)

再由式(15),(19),(20)得H1<∞.

其次证明H2<∞. 方法类似于H1<∞的证明,由引理3得

因为要用引理2和Cr不等式处理式(13),所以式(13)中q的取值可以为1,故令式(13)中q=1,再用Cr不等式得

由g,gj的定义,得

由式(19)得

(21)

因此H2<∞.

最后证明H3<∞.

由式(1),(3),(8),(9)得

当p>1,2αp>1时,由式(4),(19)得

由H12<∞和式(22)可得H3<∞. 从而由式(11)～(22)可得式(6)成立.