线性二阶锥权互补问题的非精确非单调光滑化牛顿法

迟晓妮,刘文丽,刘三阳,赵 敏

(1. 桂林电子科技大学 数学与计算科学学院,广西密码学与信息安全重点实验室,广西 桂林 541004; 2. 桂林电子科技大学 数学与计算科学学院,广西自动检测技术与仪器重点实验室,广西 桂林 541004; 3. 西安电子科技大学 数学与统计学院,西安 710071)

0 引 言

作为互补问题(CP)的推广,权互补问题(WCP)在大气化学、多体动力学、经济学等领域的一些均衡问题中应用广泛[1]. 本文考虑线性二阶锥权互补问题(LWSOCCP),即给定M∈n×n,q∈n×n,权向量w∈K,找到一向量对(x,s)∈n×n,使得

x∈K,s=Mx+q∈K,x∘s=w,

(1)

这里K为n维二阶锥,即

K∶={x=(x1,x2)∈×n-1: ‖x2‖≤x1},

其中‖·‖表示Euclid范数. 当w=0时,LWSOCCP(1)退化为线性二阶锥互补问题(LSOCCP):

x∈K,s=Mx+q∈K,x∘s=0.

由于WCP中存在非零权向量,其理论和算法比CP更复杂,因此目前关于WCP的研究文献报道较少,且大多仅限于n上. Potra[1]最早提出了WCP的概念,并研究了求解WCP的两种内点算法；Tang[2]给出了求解线性WCP的非单调光滑化牛顿法；Chi等[3]研究了Euclid Jordan代数上水平线性WCP解的存在性与唯一性.

在优化问题求解[4]中,光滑化牛顿法是一种有效的算法[5-6],其主要思想为先将原问题转化为与之等价的方程组,然后用光滑化算法对该方程组进行求解,从而得到原问题的解. 与内点算法[7-8]不同,光滑化牛顿法不要求初始点和中间迭代点严格可行[9]. 此外,光滑化牛顿算法每次迭代都需精确求解方程组,但当初始点离解较远时,精确线搜索通常效率不高,因此本文采用非精确线搜索,从而减少计算工作量.

本文结合Fischer-Burmeister函数和Natural-Residual函数[2],给出二阶锥上权互补问题的一个新的含参数光滑函数,并基于该函数,提出新的求解LWSOCCP的非精确非单调光滑化牛顿法. 算法采用非单调线搜索技术,提高了找到全局最优解的可能性及收敛速度,数值算例结果表明算法有效.

1 预备知识

对任意x=(x1,x2)∈×n-1,s=(s1,s2)∈×n-1,定义K上的Jordan积[10]为

x∘s=(xTs,x1s2+s1x2),

其单位元e∶=(1,0,…,0)T∈n,且x2∶=x∘x. 对任意x=(x1,x2)∈×n-1,定义箭形矩阵[10]为

其中I为(n-1)阶单位矩阵. 易证x∘s=Lxs,Lx+s=Lx+Ls.Lx是正定(半正定)矩阵当且仅当x∈intK(x∈K).

引理1[10]对任意x,s∈n,w≻K0,有

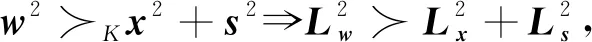
(2)

w2≻Kx2⟹w≻Kx.

(3)

若将式(2)和式(3)中“≻”替换为“±”,结论也成立.

引理2[11]对任意a,b,u,v∈n,若a≻K0,b≻K0,a∘b≻K0满足〈u,v〉≥0和a∘u+b∘v=0,则u=v=0.

2 光滑函数及其性质

对于LWSOCCP(1),构造一个新的含参数光滑函数φτ(μ,x,s):+×n×n→n:

其中w∈K为给定权向量,参数τ∈[0,4). 当w=0时,φτ(μ,x,s)退化为LSOCCP光滑函数

对任意τ∈[0,4),有

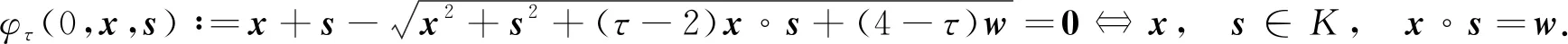
(5)

下面基于含参数光滑函数(4),将LWSOCCP(1)转化为含参数光滑方程组. 令z∶=(μ,x,s)∈+×n×n,定义函数

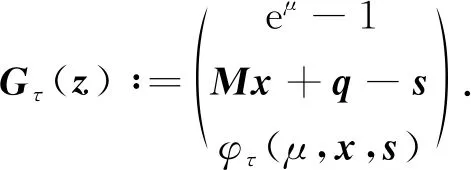
(6)

由式(1)和式(4)～(6)知,(x*,s*)是LWSOCCP(1)的解,且μ*=0 ⟺Gτ(z*)=0.

定理1令z∶=(μ,x,s)∈+×n×n,τ∈[0,4),则下列结论成立:

1)Gτ(z)全局Lipschitz连续,处处强半光滑,且在点z∶=(μ,x,s)∈++×n×n处连续可微,其Jacobi矩阵为

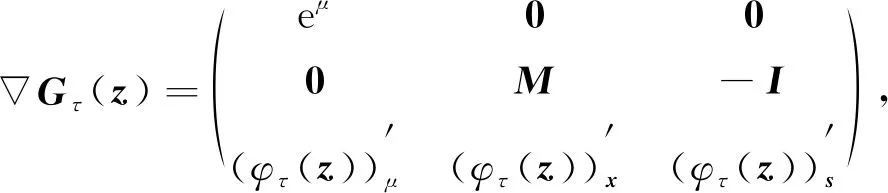
(7)

其中

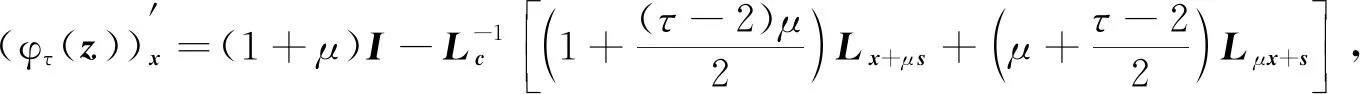
(8)

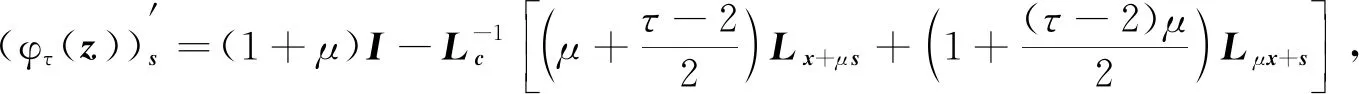
(9)

2) 若M为半正定矩阵,则Gτ(z)在任意点z∶=(μ,x,s)∈++×n×n处可逆.

证明: 1) 因为

故由文献[12]中定理3.2易证结论成立.

2) 令Δz∶=(Δμ,Δx,Δs)∈×n×n是Gτ(z)零空间中任一向量,则只需证Δz=0. 由式(7)知

Δμ=0,

MΔx-Δs=0,

(10)

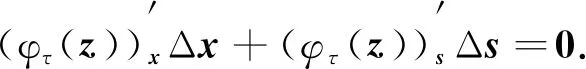
(11)

将式(11)两端左乘Lc,得

整理式(12)有

从而

对任意μ>0,由c的定义和w∈K,有

因此由引理1得

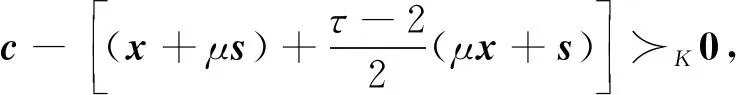
(15)

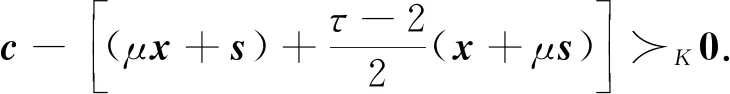
(16)

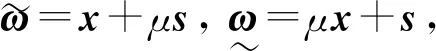
所以

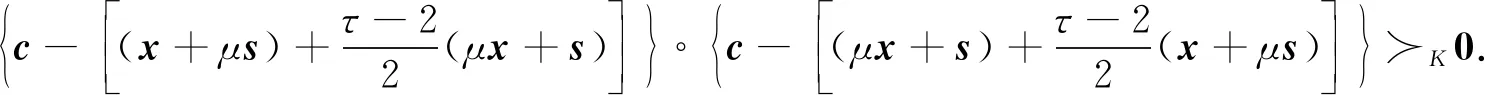
(17)

又因为M为半正定矩阵,故由式(10)知〈Δx,Δs〉=〈Δx,MΔx〉≥0,从而有

〈Δx+μΔs,μΔx+Δs〉=μ(‖Δx‖2+‖Δs‖2)+(1+μ2)〈Δx,Δs〉≥0.

(18)

由式(14)～(18)和引理2有Δx+μΔs=0,μΔx+Δs=0,故由式(10)得Δx=0,Δs=0,结论成立. 证毕.

3 非精确非单调光滑化牛顿法

下面基于光滑函数(4),给出求解LWSOCCP(1)的非精确非单调光滑化牛顿法,且在适当的假设条件下证明算法适定.

定义函数Hτ:+×n×n→+为Hτ(z)∶=‖Gτ(z)‖2.

算法1LWSOCCP的非精确非单调光滑化牛顿法(INS).

选择常数σ,δ∈(0,1),p∈[0,1],μ0>0. 取ρ∈(0,1)和ξ∶=‖Gτ(z0)‖+1,使得μ0ρξ<1. 令z0∶=(μ0,x0,s0)∈×n×n为任意初始点,

Q0=1,C0∶=Hτ(z0),T(z0)=ρmin{1,‖Gτ(z0)‖1+p}.

设序列{υk}满足υk∈[0,1-μ0ρξ]. 选取ηmin和ηmax,使得0≤ηmin≤ηmax<1. 置k∶=0.

步骤1) 若Hτ(zk)=0,则算法停止;

步骤2) 解下列方程组得搜索方向Δzk∶=(Δμk,Δxk,Δsk)∈×n×n:

(19)

其中T(zk)=min{ρ,ρ‖Gτ(zk)‖1+p,T(zk-1)},‖r(zk)‖≤υk‖Gτ(zk)‖;

步骤3) 令αk为1,δ,δ2,…中使得下式成立的最大值:

Hτ(zk+αkΔzk)≤[1-σ(1-μ0ρξ-υk)αk]Ck;

(20)

步骤4) 令ηk∈[ηmin,ηmax],zk+1∶=zk+αkzk,且

Qk+1∶=ηkQk+1,

(21)

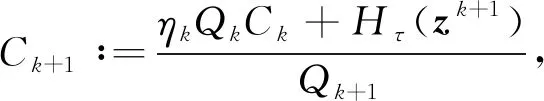
(22)

置k∶=k+1,转步骤1).

定理2令{Ck},{T(zk)},{zk}是算法1生成的迭代序列,则:

1) {Ck}单调递减;

2) 对任意k≥0,有Hτ(zk)≤Ck且{T(zk)}单调递减;

3) 对任意k≥0,有μk>0且μ0T(zk)≤μk.

证明：类似文献[13]中注3.1和文献[14]中引理1可得结论.

定理3若M为半正定矩阵,则算法1适定.

下证算法1中步骤3)适定. 对任意α∈(0,1],定义

L(α)=Gτ(zk+αΔzk)-Gτ(zk)-αGτ(zk)Δzk.

(23)

由定理1中1)知Gτ(·)在任意点zk=(μk,xk,sk)∈++×n×n处连续可微,则

‖L(α)‖=ο(α).

(24)

对任意k≥0,由T(zk)的定义知,当‖Gτ(zk)‖≤1时,有

T(zk)≤ρ‖Gτ(zk)‖1+p≤ρ‖Gτ(zk)‖;

(25)

当‖Gτ(zk)‖>1时,有

T(zk)=ρ≤ρ‖Gτ(zk)‖.

(26)

因此由式(25)～(26)得

T(zk)≤ρ‖Gτ(zk)‖.

(27)

由定理2中2)和式(6)知,对任意k≥0,有

故eμk≤ξ. 从而由式(19),(23),(24),(27)知,对任意α∈(0,1],有

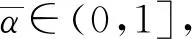
Hτ(zk+αΔzk)≤[1-σ(1-μ0ρξ-υk)α]Ck.

故算法1中步骤3)适定. 从而算法1适定.

4 收敛性分析

下面证明算法1的全局收敛性和局部超线性收敛性.

定理4设M为半正定矩阵,{zk}是算法1生成的迭代序列,则{zk=(μk,xk,sk)}的任一聚点z*∶=(μ*,x*,s*)都是Gτ(z)=0的解.

证明: 不失一般性,设当k→∞时,{zk=(μk,xk,sk)}收敛到z*∶=(μ*,x*,s*). 由定理2中1)知{Ck}为收敛序列,即

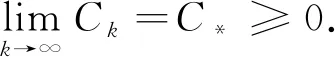
(28)

由定理2中2)知

0≤‖Gτ(zk)‖2=Hτ(zk)≤Ck≤Ck-1≤C0,

(29)

所以序列{Hτ(zk)}有界,因此必存在收敛子列{Hτ(zk)}k∈J,其中J⊆{0,1,2,…,k,…}. 故

反证法. 设Gτ(z*)>0,则C*>0,考虑下列两种情形:

(i) 若对任意k∈J有αk≥α*>0,其中α*为某固定常数. 由式(20)～(22)得

由{Ck}有界知

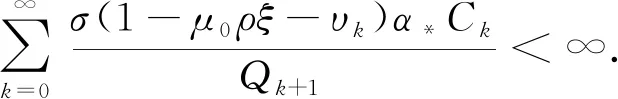
(31)

又由式(21)得

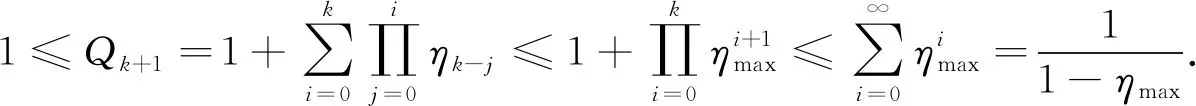
(32)

(33)

从而由定理2中2)有

(34)

由定理2中3)知

的解. 由式(29),(33)得Hτ(z*)≤C*≤Hτ(z*),因此

Hτ(z*)=C*.

(35)

从而

2Gτ(z*)TGτ(z*)Δz*≥-σ(1-μ0ρξ-υ*)C*.

(36)

又由式(27)和式(35)知

T(z*)‖Gτ(z*)‖≤ρHτ(z*)=ρC*,

(37)

于是由式(36)～(37)有

即σ(1-μ0ρξ-υ*)≥2(1-μ0ρξ-υ*),与σ∈(0,1)矛盾. 故结论成立.

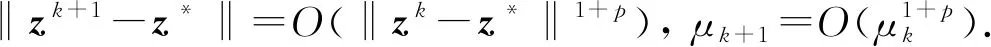
证明: 类似文献[4]中定理8可证.

5 数值算例

下面用MATLAB R2014在Intel(R) core(TM)i5-5200 CPU 2.7 GHz,4.0 GB内存,Windows 7操作系统的计算机上编程,验证算法1的性能,且每个算例均随机生成15个问题进行求解. 参数取值为σ=0.04,μ0=0.01,δ=0.5,ρ=0.02,υk=2-k,τ=1. 令0=(0,0,…,0)T,e=(1,0,…,0)T,1=(1,…,1)T. 随机生成矩阵N∈n×n和向量q∈n,令矩阵M=NTN,s=Mx+q,以‖G(z)‖≤10-6为算法终止条件,(x0,s0)为初始点,记AIT为平均迭代次数,ACPU为平均CPU时间.

例1给定权向量w=(1,0.1×1),令ηk=0.1,n=100. 表1列出了算法1求解不同初始点和不同p值LWSOCCP的数值结果. 由表1可见,不同初始点对算法所需的AIT和ACPU影响明显,而p值对算法影响较小.

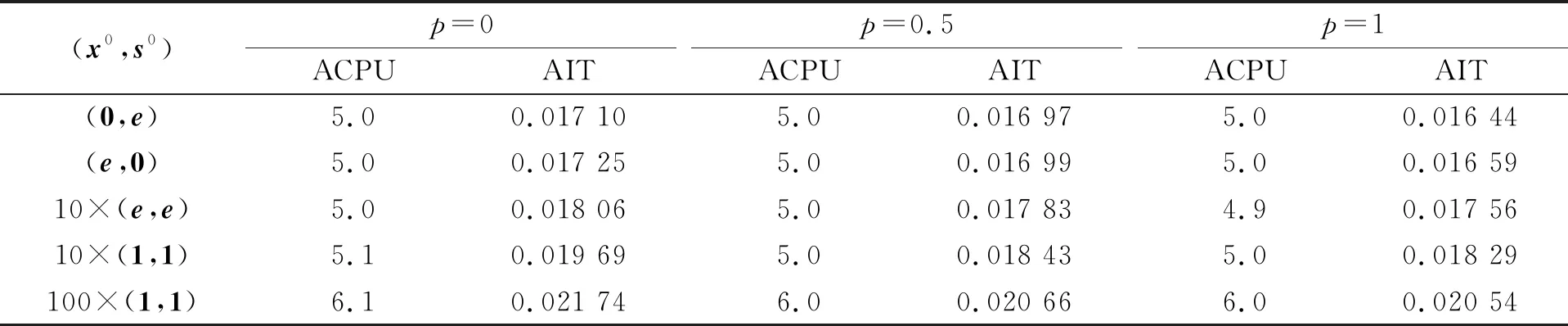
表1 算法1求解不同初始点和不同p值LWSOCCP的数值结果

例2给定权向量w=e,令p=1,初始点(x0,s0)=(e,e),问题规模从200维到600维. 用算法1求解不同ηk值的LWSOCCP,并比较算法1(INS)与采用精确线搜索的光滑化算法NS(nonmontone smoothing)[13]求解LWSOCCP的数值结果,结果列于表2. 由表2可见,算法1采用非单调线搜索(ηk≠0)比采用单调线搜索(ηk=0)所需的ACPU和AIT少,且在相同条件下,算法1比算法NS求解LWSOCCP的效果更好.

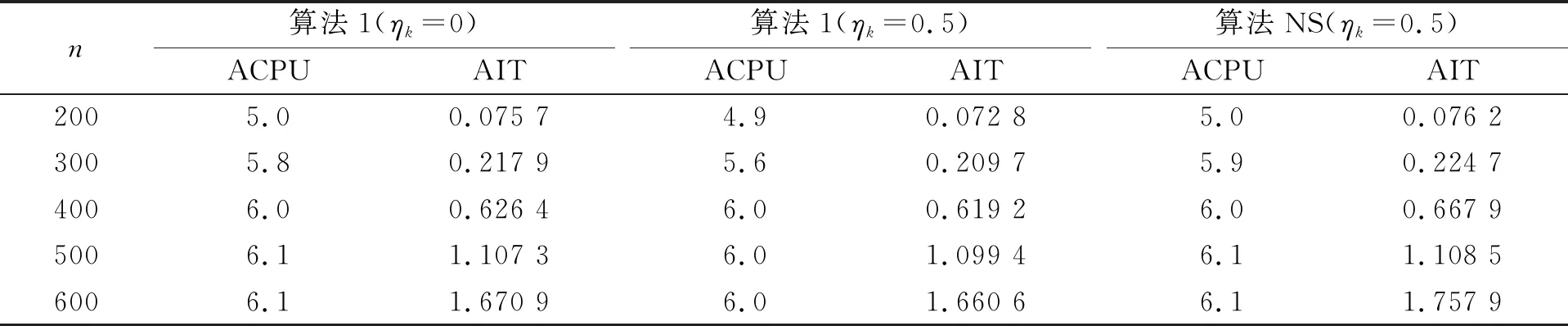
表2 算法1和算法NS求解LWSOCCP的数值结果

综合表1和表2可见,算法1可有效求解LWSOCCP,且收敛速度快,迭代次数少,因而算法性能稳定.