基于免疫遗传算法的油田地面环形集输管网优化方案

周金勇 胡光兴 何伟 张宗前 马延芳

1中国石油青海油田公司采油四厂2中国石油青海油田公司采油三厂3中国石油青海油田公司采油一厂

随着计算机智能技术的发展，智能算法在工业效益优化上的优势逐渐体现出来，同时对已有算法进行优化是当前的研究热点。以免疫遗传算法为例，KUMAR 将这种算法与粒子滤波相结合，利用免疫系统机制对目标进行有效的跟踪，结果证明这种方法的系统识别性能显著提高[1]。SUHAIMI 等将标准遗传算法与免疫算法过程相结合，并将其用于计算机网络的入侵预测中[2]。IDRISSI等则在组合策略优化问题求解过程中引入了改进遗传算法，并且证明了克隆算法可以有效改进遗传算法性能[3]。ZAINAELDIN等探讨了不同思路改进的遗传算法在无线传感器网络优化中的效果，其结果证明IDDTGA算法在网络动态部署上具有较好的优越性[4]。综上可以看出，国内外研究主要涉及对油田管网的结构和布局优化，利用智能算法确定油田的最优成本方案，以及油田中原油的输送问题，较少涉及利用遗传算法对油田地面集输管网进行优化设计。

油田地面环形集输管网的优化设计至关重要，能够提高油田地面工程的设计水平和效率。曹迪等在油田集输管网的优化布局研究中，提出在划分油田井组和优化集气站站址的基础上建立优化布局模型，并利用遗传算法进行求解，研究结果对油田布局具有一定参考价值[5]。王博弘等在研究油田集输管网的拓扑结构优化时，提出寻找集输管网最优环的方法，以管网总费用为目标函数建立相应优化模型，并验证了该模型的有效性[6]。孙涛等在对油田集输管网设计进行优化时，构建了优化设计模型，并利用K-means算法求解结果，最后利用实例验证了算法的收敛性和稳定性[7]。许继凯等为了确定油气输管网结构布局，以井站间产量为目标函数，以井站连接关系为变量建立了优化模型，并利用实例验证了该模型的有效性[8]。

因此，此次研究在免疫遗传算法的基础上，构建油田地面环形集输管网的数学模型，以得到其建立的最优方案

1 优化设计数学模型

1.1 免疫遗传算法

近年来，遗传算法的应用越来越广泛，其算法的理论灵感来源于生物学中的遗传学观点，借助生物学中染色体的概念，将待求解的所有问题表示为一群染色体，并置于一定的环境中，对所有问题进行再生、交叉、变异等运算，以求得问题的最优解。遗传算法包含五个要素，分别是设定编码方案、产生初始种群、计算种群适应度、设定控制参数以及对遗传进行相应操作，这些要素构成了遗传算法的主要运算过程。免疫遗传算法是遗传算法中的一种，主要是为解决传统遗传算法中效率不高的问题而提出，以生物免疫机制为基础对传统遗传算法进行的改进[9]。相较于传统遗传算法，免疫遗传算法能保证解的全局性，在解的计算精度和优化速度方面都有较大的提升，因而研究运用免疫遗传算法进行油田地面环形集输管网优化模型的设计具有重要意义。

2.2 模型建立

地面环形集输管网所包含的设计变量有两个，分别是油田每条管线的管径和油田各级站的所在位置。在地面环形集输管网优化前，先对油田井组进行划分，划分依据是油田集输半径的大小，在此基础上利用免疫遗传算法进行数学模型的求解。优化设计方案的实现途径是对集输半径进行变换，设计变量表示为OPT{{x,y},{D} }。OPT 为命令行参数选项，{x,y} 为井组坐标，D为管径，mm。

地面环形集输管网优化方法的约束条件包括很多，以油井管线进出站的温度、管径的圆整选择、管线的承载、油井井口的回压以及压力约束为主[10]。由于此次研究油田的地形条件复杂，所以在研究时扩大了油田地面环形管网的集输半径。扩大集输半径后会使每个站所辖油井数增加，因而需要对油井进行相应的分组。常用的油井分组方法包括随机圆形分组、格式化圆形分组、等间距以及缩小等间距分组法，这些分组法均利于控制集输半径，但会存在相距很近的油井大概率不能分到一组的问题[11]。因而结合油井和油井集输半径的特点，采用改进的边界搜索法对油井进行分组。井组划分完成后需要计算各个井组的中心位置，以及离差平方和，j井组中的位置与编号k的油井的离差平方和计算方法如式（1）所示。

式中：i∈j为第j个分组的第i口油井，当该油井的位置表示为(xij,yij)时，则Lij为第j个分组的第i口油井与第j个转油站之间的距离。

计算出离差平方和后，根据各个油井到转油站的距离再次对油井进行划分，划分时建立数学模型。设井组的总数为N，则再次划分的数学表达如式（2）～（7）所示。

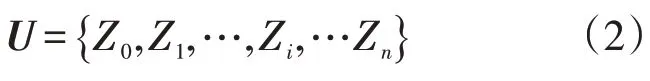
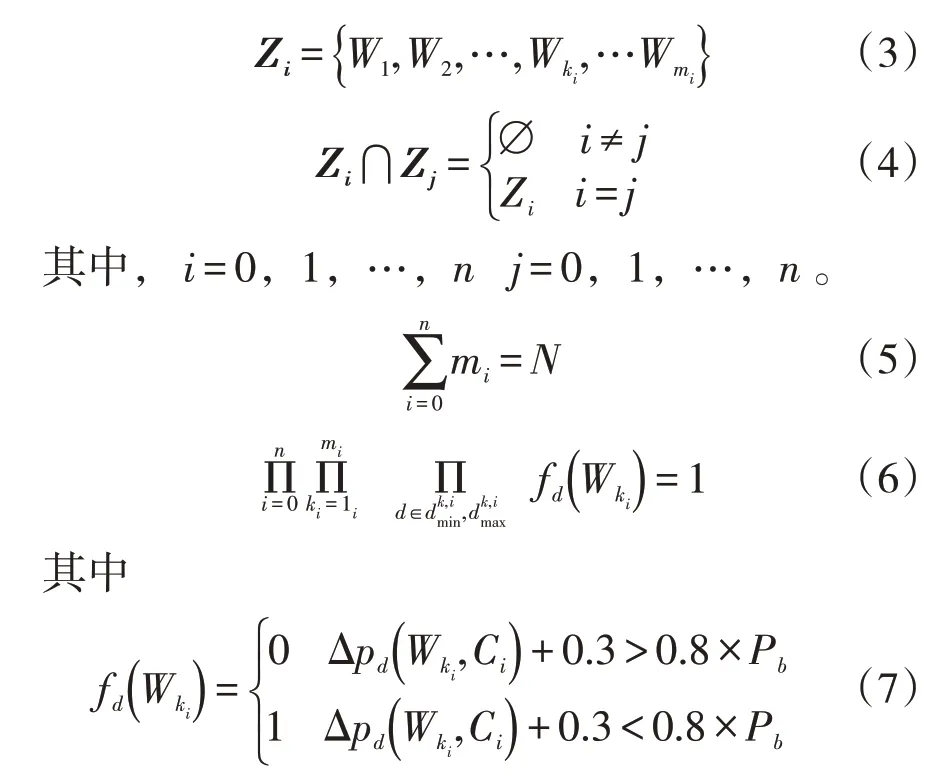
式中：U为再次划分井组后各个子井组的集合；Zi为再次划分井组后得到的第i个子井组；为所得子井组Zi中编号为k的子油井；mi为划分的井组Zi所辖的子油井数目；Ci为划分的子油井Zi的中心，该中心通过该子油井组所包含的所有油井的平均纵坐标、平均横坐标计算得到；为压降，MPa，通过油井Wki到子油井Ci的管径距离计算而得；d为管径距离，m；为一个管径系列，该系列根据子油井组Zi中所辖油井到子组的中心位置Ci的管道距离计算而得，这个管径系列能够使得该油井管道不超过经济流速范围，符合油田输出管网国家标准[12]。

从免疫遗传算法在油田地面环形集输管网规划的运算过程[13]（图1）可以看出，免疫遗传算法运算包括选择、交叉、变异运算等，其流程以群体开始，此次研究中的群体为油井。在该模型运算过程中，对油田地面环形集输管网进行选择、交叉以及变异等运算，而后在运算基础上针对下一个地面环形集输管网进行同样的运算，再对运算结果进行解码，以得到相应的解集合，最后对所求对象进行个体评价。此次研究是对油田地面环形集输管网的优化方案进行评价。

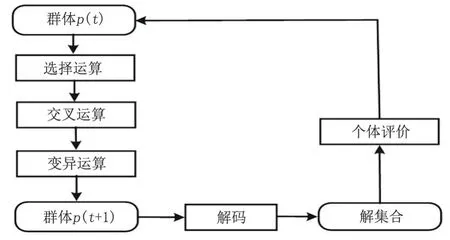
图1 免疫遗传算法过程Fig.1 Immune genetic algorithm process

1.3 模型求解

对上述所建立的数学模型进行求解，利用模糊聚类法求出模型中的油井子组集合U[14]。具体求解过程包括以下几个步骤：

（1）首先设原始井组的数量为D，求解之前先遍历所有油井井组的各个油井，找到符合式（8）的所有油井，并将符合条件的油井划为一个子组，记为Z0，将该子组中的油井数目记为m0，这些油井的压力充足，可直接连接到建立完成的转油站，这些油井需要满足的条件如式（8）所示。

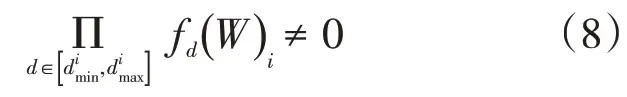
（2）建立模糊矩阵，并将其表示为A。设n个对象的集合为X={x1,x2,…,xn}，可以用相应的指标对该集合中的每一个对象进行评价，设指标数目为m，则指标评价的集合可以表示为据此可以得到模糊矩阵如式（9）所示。

其中，矩阵中的每个元素都分别对应一个油井的位置。

（3）由于第二个步骤中所建立的原始模糊矩阵A中仅存在一个指标，所以不会由于指标和量纲不同而对模糊聚类造成影响，因而在求解模型时也不需要对数据进行标准化。在此直接建立模糊矩阵A的相似矩阵R=()rij，其中i,j=1,2,…,N-m0，该矩阵的构造方法如式（10）所示。

式中：R为集输半径，m；L(xi,xj)为第i口油井与第j口油井之间的距离，m。

（4）建立一个等价矩阵R*。一般情况下，在第三步中所建立的相似矩阵是不具备传递性的，只具有对称性与自反性。因此，为了使矩阵具有传递性，需要得到原相似矩阵的传递闭包矩阵，所用到的转换方法为平方自合成法，该传递闭包矩阵就是与上述相似矩阵等价的矩阵R*。在上述所构建的相似矩阵R中，肯定存在一个最小自然数k(k≤N-m0)，能够使得R*=Rk，并且对于任意一个大于k的自然数q，都存在Rq=Rk。因而，在模型求解总次数少于N-m0次的情况下，存在一个与相似矩阵等价的模糊矩阵R*。利用平方自合成法可求得矩阵R如式（11）所示[15]。

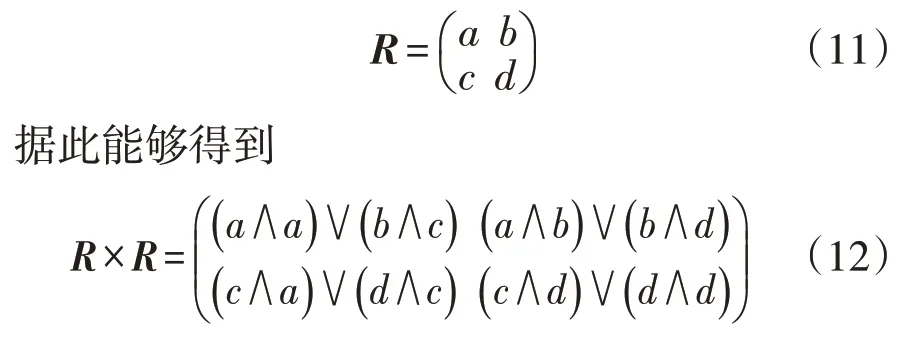
（5）对油井进行模糊聚类。构建完成模糊矩阵R*以后，对油井进行模型求解，具体过程如图2所示。可以看出，该流程以遗传算法的变异、交叉、选择运算等为基础，设定油田组数初始值，进行相应的求解运算，当最终油田组数与预期结果相符时，则结束免疫遗传运算。

2 地面环形集输管网优化验证

2.1 实例参数和障碍物信息

运用油田地面环形集输管网的实例验证上述模型的有效性，该油田的油井涉及多种通用参数（表1）。

图2 免疫遗传算法应用于集输管网流程Fig.2 Immune genetic algorithm applied to the flow of gathering and transmission pipeline network

表1 油田油井通用参数Tab.1 General parameters of oil wells in oilfields

从表1 中可以看出，通用参数包括油井压力、油井温度、原油密度、天然气相对密度、电动机功率、加热炉效率以及泵机组效率等，其中油田中的油井温度以及压力需要特别注意。另外，通用参数可以根据油田油井的实际情况进行设置。验证模型的实例还涉及障碍物数据，由于地形的复杂性，障碍物数据难以通过现场调研获得，因而研究时假设两个障碍物信息，具体信息如表2所示。

表2 障碍物信息Tab.2 Obstacle information

从表2中可以看出，假设的两个障碍物编号为0 和1，0 号障碍物的顶点编号为0～3；1 号障碍物的顶点编号为0～4。每个障碍物所对应的顶点都分别以x坐标、y坐标表示。其中x坐标都在19 200左右，而y坐标都在4 100 左右，说明所假设的障碍物位置是比较接近的。此外，该实例还涉及油井管线的规格及费用、各级站的费用等。油井管线规格采用国家标准，其报价可以根据经济预算进行适当调整；各级站包括转油站、联合站以及增压点等，其报价根据大小的不同在几十到百万元不等。

2.2 设计有效性验证

油井参数设置完成以后，对油井的集输管网进行优化设计，并计算得到相应的结果，包括油区最佳集输半径和油田地面环形集输管网最优设计方案。其中，实例油区的集输半径与费用关系如表3所示。

表3 地面环形集输管网集输半径与费用Tab.3 Gathering radius and cost of ground circular gathering and transportation network

从表3中可以看出，大部分情况下，随着集输半径的增加，地面环形集输管网造价也逐渐增加，仅半径为2 km 时，造价不如集输半径为1 km 时高。基本上地面环形集输管网的造价与集输半径呈正相关关系。为更加清楚地表示集输半径与地面环形集输管网之间的关系，将上述表格中的数据以图形的形式表达出来（图3）。

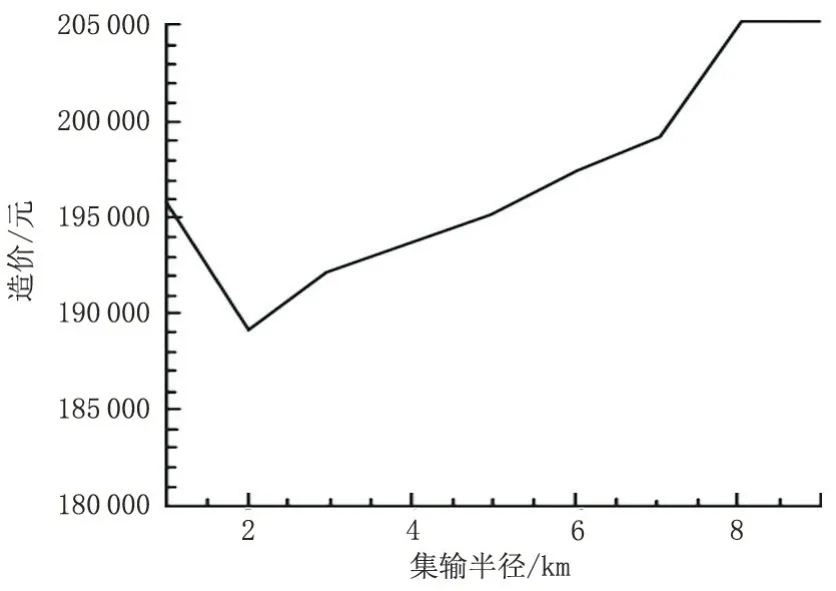
图3 集输半径与地面环形集输管网费用关系Fig.3 Relationship between gathering radius and cost of ground circular gathering pipeline network

从图3中可以较为直观地看出，地面环形集输管网的造价随集输半径的增大而增加，仅在集输半径为2 km 时，造价相较集输半径1 km 时有所减少。当集输半径超过8 km 后，油田地面环形集输管网的造价不再随着集输半径的增加而发生变化。

结合表3和图3可以得出，集输半径为2 km时可以使得系统的造价最省。如果设计油田地面环形集输管网时取较小的集输半径，以1 km 为例，则会建立较多的转油站，过多的建站数量会分担一定的产量，使得每个站的产量都较低，最终导致整个系统的经济效益降低；当集输半径扩大，如达到2 km 时，建站数量会相应减少，其所辖油井数量也会增多，建站费用减小幅度较大，使得整个系统的总造价降低；随着集输半径超过2 km，由于增设了增压泵使得系统总造价再次增加；而当集输半径超过8 km 时，所有油井的地面环形集输管网都被划分到同一个组，分组情况和其他参数一致，因而免疫遗传算法迭代的次数足够多时，系统总造价基本保持不变。

表4为集输管网在最佳半径下各级站的最优方案实例，包含10个转油站和1个联合站，它们的坐标位置都是在19 200±100，4 100±100 这个范围内，坐标与坐标之间的距离均小于2 km，说明各级站的位置距离较近，划定在一个区域范围内；就油流量而言，10 个基站的油流量大都在2～3 m3之间，其中转5、转7 以及转8 三个站的油流量大于3 m3，联合站的油流量为31.84 m3；就气流量而言，10 个基站的气流量大部分在0.1～0.2 m3之间，转5、转7以及转8的气流量都大于0.2 m3，联合站的气流量为2.078 m3；就最低出站压力而言，仅转3和转6的最低出站压力在40×104MPa左右，其余站的最低出站压力都在100×104～300×104MPa 之间，联合站的最低出站压力282 650.2 MPa；就最低出站温度而言，各级站的最低出站温度都位于18～20 ℃之间，联合站的最低出站温度为18.1 ℃。

表4 各级站最优方案实例Tab.4 Optimal scheme examples of stations at all levels

3 结论

将免疫遗传算法应用于油田地面环形集输管网的优化中，可以有效优化地面环形集输管网的设计方案。本次研究结合某油田地面环形集输管网的实际情况，以免疫遗传算法为基础，构建地面环形集输管网的优化数学模型，并对优化模型进行求解，再运用优化运算实例对模型的有效性进行验证。研究结果表明，当集输半径小于8 km 时，地面环形集输管网的造价与集输半径呈正相关，集输半径为2 km 时，应用地面环形集输管网优化设计方案，整个系统造价最低。通过运算实例能得到地面环形集输管网优化的最佳方案，即油田各级站划定在一定范围，且集输半径以2 km 为最佳，说明在免疫遗传算法的基础上所构建的优化数学模型是有效的。本次研究能够验证免疫遗传算法在地面环形集输管网优化中的有效性，其广泛适用性还有待进一步研究。