机械式自动垂直钻具上盘阀开口角度的优化分析

张 龙，张 凯，柴 麟，李国民，周 琴，刘宝林，李然然

（1.中国地质大学（北京）工程技术学院，北京100083；2.自然资源部深部地质钻探技术重点实验室，北京100083）

动态机械式自动垂直钻具是根据偏重块的重力感应，利用稳定平台的运动，借助执行机构的推靠装置，在直井作业中进行自动防斜纠斜的。因其具有结构简单、成本低、适应性广等优势，在高陡高斜地区的直井作业中广泛使用［1-2］。过大的井斜会导致井眼偏离设计轨迹，给勘探工作带来很大影响，而且还会使钻柱磨损加快，甚至出现断裂的情况，给钻探工作造成巨大的安全隐患及经济损失。所以，在保证井眼质量的前提下提高纠斜速度是优化机械式自动垂直钻具的先决条件之一。

苏义脑等［3-4］对自动垂直钻具的运动形式、纠斜原理进行了研究，为之后钻具的优化设计提供了理论指导。狄勤丰等［5-7］在对钻具执行机构推靠力变化规律的研究中发现，稳定平台中上盘阀的开口角度会影响执行机构的推靠力，并提出可以通过改变上盘阀的开口角度来优化纠斜，但并未深入分析上盘阀开口角度对井眼螺旋程度、纠斜效果的影响。本文理论分析了上盘阀开口角度对钻具整个纠斜过程的影响，并与现有的试验结论进行对比；设定表征井眼螺旋程度和纠斜效果的参数，并分析其与上盘阀开口角度的关系，最终得到上盘阀开口角度的最优解，以期为自动垂钻工具的优化设计提供指导。

1 钻具稳定平台分析模型的简化和建立

机械式自动垂直钻具的纠斜原理如图1 所示。在钻具纠斜时，上盘阀的环形槽中线会稳定在井眼高边，下盘阀通常设有多个开孔，每个开孔均与底部执行机构中的流道相连通［8］。下盘阀随钻柱作顺时针转动时，下盘阀开孔会与上盘阀开口重合，使流道导通；流道导通后，钻井液在柱塞（每个流道对应一个柱塞）两边形成流道处压力和环空压力的压力差，使巴掌（即图1中的推靠机构）伸出并推靠井壁；在此推靠力作用下，在钻头处产生的反向的侧向切削力使钻头切削井眼低边岩石，从而使井眼逐渐回到垂直位置，最终实现纠斜［9］。

图1 机械式自动垂直钻具的纠斜原理示意Fig.1 Schematic of restoring principle of mechanical automatic vertical drilling tool

为分析上下盘阀相对运动对钻具纠斜的影响规律，以常用的三推靠巴掌垂直钻具为例，对其上下盘阀进行简化（如图2所示），建立钻具稳定平台分析模型。图2中：虚线扇形所示为上盘阀开口，开口角度为α，并静止在井眼高边方向；实线圆代表有3个均匀分布开孔的下盘阀，其以角速度ω匀速随钻柱作顺时针转动。为简化分析，借鉴彭勇等［6-7］的研究经验，忽略下盘阀流道直径大小以及巴掌推出和收回时的滞后影响。F 为每个巴掌的实际推靠作用力。以上盘阀圆心为原点，以上盘阀环槽中线为0°刻度线并对位为±180°刻度线，建立角坐标系。Fx、Fy分别为推靠力在扩径方向和导向方向的分量，θ为推靠力与上盘阀环槽中线的夹角。

图2 三推靠巴掌垂直钻具上下盘阀简化图Fig.2 Simplified diagram of upper and lower disc valve of vertical drilling tool with 3 push hands

2 推靠力变化规律的分析

2.1 推靠力变化的理论分析

从图2可知，上盘阀开口角度的改变会影响钻具纠斜过程中巴掌伸出的数量，从而引起推靠合力大小的变化。如图3所示，当上盘阀开口角度由α1变为α2时，流道导通数量由1 个变为2 个，推靠力由F变为F'。对由上盘阀开口角度变化引起的推靠力的变化规律进行分析。由于下盘阀的3个开孔是均匀分布的，每个开孔之间的角度为120°。α会影响巴掌伸出的数量，所以将α分为3个区间进行分析：α=0°～120°时，巴掌伸出0或1个；α=120°～240°时，巴掌伸出1或2个；α=240°～360°时，巴掌伸出2或3个。巴掌伸出进行纠斜的推靠力都来源于柱塞两侧的液压差，则各个巴掌的推靠力均为：

式中：Δp为柱塞两侧的液压差；s为柱塞的有效接触面积。

图3 不同上盘阀开口角度下推靠作用力示意Fig.3 Schematic of push force at different opening angles of upper disc valve

合成各个巴掌的推靠力，可以进一步得到推靠合力与巴掌伸出数量的关系，如表1所示。

表1 推靠合力与巴掌伸出数量的关系Table 1 Relationship between resultant push force and the number of outstretched hands

由于下盘阀的3 个开孔均匀分布，且作圆周运动，其运动状态具有周期性。设定下盘阀中一个开孔的初始位置位于上盘阀开槽的右极限位置，令其转角为γ( γ=ωt )。0°＜γ ≤120°时，在不同的上盘阀开口角度下，推靠合力与下盘阀转角的关系如表2所示。

动态机械式自动垂直钻具的特点在于底部的巴掌会与钻柱一起转动。巴掌在转动的同时进行纠斜，会使推靠合力的方向发生变化。经过计算可以得到在不同的上盘阀开口角度下推靠合力方向（用θ 表示）与下盘阀转角的关系，如表3所示。

由表3 可知，上盘阀开口角度在3 个不同区间时，推靠合力有不同的变化规律。为了更加清晰地分析推靠合力的变化差异，在上述3个上盘阀开口角度区间中分别取值，并做出相应的推靠力变化曲线进行对比。α=100°，200°，300°时，推靠合力大小和方向随下盘阀转角的变化曲线如图4和图5所示。

表2 推靠合力与下盘阀转角的关系（0°＜γ ≤120°）Table 2 Relationship between resultant push force and rotation angle of lower disc valve（0°＜γ ≤120°）

表3 推靠合力方向与下盘阀转角的关系（0°＜γ ≤120°）Table 3 Relationship between the direction of resultant push force and rotation angle of lower disc valve（0°＜γ ≤120°）

图4 推靠合力大小随下盘阀转角的变化曲线Fig.4 Changing curve of resultant push force magnitude with rotation angle of lower disc valve

结合表2 和图4 可知：当α=0°～120°、240°～360°时，出现推靠合力大小不恒定的情形；当α=120°～240°时，整个推靠过程相对平稳。

由图5可知：当α=0°～120°、240°～360°时，θ出现不连续的情况；当α=120°～240°时，θ 是连续的，只是其大小发生了变化。因此，为保证推靠合力的持续稳定输出，α应尽量控制在120°～240°。

图5 推靠合力方向随下盘阀转角的变化曲线Fig.5 Changing curve of resultant push force direction with rotation angle of lower disc valve

2.2 推靠力变化理论分析结果的验证

为了验证推靠力变化理论分析结果的准确性，笔者参考文献［10］中的实验数据进行对比分析。选取机械式自动垂直钻具上盘阀开口角度为120°，巴掌数量为3个。在井斜角为2.5°，转速为30 r/min时，推靠力响应过程如图6 所示［10］。由图6 可知，3 个巴掌的推靠力均有一个“升高—平稳—降低—平稳”的过程，分别对应工具的“升压—高压稳压—泄压—低压稳压”的过程。图7示出了在上述工况下推靠力的理论分析结果。

图6 推靠力测试曲线（井斜角为2.5°，转速为30 r/min）Fig.6 Test curve of push force（well inclination of 2.5° and rotation speed of 30 r/min）

比较图6、图7可知，由于在理论分析时忽略了摩擦、振动等对推靠力的影响，理论曲线并未像测试曲线那样在稳压阶段呈现一定的波动性。因此，为了进一步验证理论分析结果的准确性，分别提取测试和理论分析中各巴掌稳压阶段的平均推靠时间，结果如表4所示。由表4可知，在稳压阶段平均推靠时间的测试值与理论值基本相同，偏差率小于10%。另外，3个巴掌平均推靠时间的测试值并不相同，存在一定的差异。这主要是由于在实际测试中存在振动以及工具零配件间存在摩擦等，会对单巴掌的推靠产生超前或滞后的影响。对各巴掌的单周期平均推靠时间进行统计，得到其实际平均推靠时间为0.665 s，可见测试值与理论值基本相同。因此，无论是从推靠力还是从推靠时间上来看，本文的理论分析具有一定的准确性。

图7 推靠力理论曲线（井斜角为2.5°，转速为30 r/min）Fig.7 Theoretical curve of push force（well inclination of 2.5° and rotation speed of 30 r/min）

表4 巴掌稳压阶段平均推靠时间的测试值和理论值Table 4 Test value and theoretical value of average push time in the pressure stable stage of hand

3 纠斜性能分析和评价

在钻具纠斜过程中，沿导向方向的导向力Fy对纠斜起主要作用，垂直于导向方向的扩径力Fx则会扩大井眼尺寸而影响井眼质量［11］。扩径力和导向力的表达式分别为：

结合表2、表3的推靠合力大小和方向与下盘阀转角的关系，可以推导出扩径力和导向力的变化规律，如表5所示。

当α=100°，200°，300°时，扩径力和导向力随下盘阀转角的变化曲线如图8 和图9 所示。由图8 可知，扩径力在不同上盘阀开口角度区间内的变化不同，但在整个纠斜过程均具有明显的周期性，呈现以120°为一个周期的循环变化。由图9可知，在纠斜过程中，导向力不断变化，且在巴掌交替作用时，导向力存在突变现象。

可见，在纠斜过程中，上盘阀开口角度会在很大程度上影响扩径力和导向力，从而影响纠斜效果。为了研究上盘阀开口角度与纠斜效果的关系，本文设定如下参数：扩径力冲量IE、导向力的波动幅值h 与突变幅度H、导向力对井眼高边产生的冲量IP。通过计算不同上盘阀开口角度所对应的参数值，来建立上盘阀开口角度与纠斜效果的关系。

表5 扩径力和导向力的变化规律Table 5 Changing rule of expanding force and guiding force

图8 扩径力随下盘阀转角的变化曲线Fig.8 Changing curve of expansion force with rotation angle of lower disc valve

图9 导向力随下盘阀转角的变化曲线Fig.9 Changing curve of guiding force with rotation angle of lower disc valve

3.1 扩径力冲量分析

扩径力垂直于导向方向，对纠斜效果没有很大的影响。但在纠斜过程中，扩径力会使钻柱的方位角产生额外变化，其大小和作用时间都会影响方位角的变化程度，所以用扩径力冲量IE作为衡量方位角变化程度的参数：IE越小，则视为井眼的螺旋程度越低，井眼质量越好。

当α=200°时，下盘阀从0°转到120°的过程中扩径力的变化曲线如图10所示。

图10 α=200°时扩径力的变化曲线Fig.10 Changing curve of expansion force with α=200°

如图10 所示，将该扩径力分为①②③④四部分，则由扩径力与下盘阀转角的关系可以得到各部分扩径力产生的冲量为：

当0°＜γ ≤120°时，综合表6 和图11可知：当0°＜α≤120°时，IE随着α的增大而增加；当120°＜α≤240°时，IE先降低至约0.134λ，后逐渐增加；当240°＜α≤360°时，IE随着α的 增大而减小，直至0 N·s；当α=180°时，IE取得最小值。因此，在推靠合力持续作用下，为降低井眼螺旋程度，提高井眼质量，α应尽量在180°附近取值。

图11 扩径力冲量随上盘阀开口角度的变化曲线（0°＜γ ≤120°）Fig.11 Changing curve of expanding force impulse with opening angle of upper disc valve（0°＜γ ≤120°）

3.2 导向力冲量分析

导向力的大小和作用时间直接关系着推靠效果。所以用导向力冲量IP作为衡量有效推靠作用的参数：IP越大，则视为导向力在纠斜过程中提供的作用越大，纠斜效果越好。

当α=200°时，在下盘阀从0°转到120°的过程中导向力的变化曲线如图12所示。

图12 α=200°时导向力的变化曲线Fig.12 Changing curve of guiding force with α=200°

当0°＜γ ≤120°时，导向力冲量与上盘阀开口角度的关系如表7所示；导向力冲量随上盘阀开口角度的变化曲线图13所示。

表7 导向力冲量与上盘阀开口角度的关系（0°＜γ≤120°）Table 7 Relationship between guiding force impulse and opening angle of upper disc valve（0°＜γ ≤120°）

图13 导向力冲量随上盘阀开口角度的变化曲线（0°＜γ ≤120°）Fig.13 Changing curve of guiding force impulse with opening angle of upper disc valve（0°＜γ ≤120°）

由表7可知，在不同上盘阀开口角度下，导向力冲量均满足：

由图13可知，随着α上不断增加，在一个周期内IP会逐渐升高，在α=180°时达到峰值，之后开始递减。可见，当α=180°时，执行机构提供的导向力冲量最大，纠斜效果最好。该结论与狄勤丰等［5］得到的在单位时间内导向机构平均作用合力的变化规律相吻合。

3.3 导向力稳定性分析

当巴掌伸出数量发生变化时，导向力会产生突变。这种突变对纠斜效果及巴掌使用寿命有影响。此外，在巴掌进行持续推靠的过程中，由于巴掌随着钻柱持续转动，导向力也存在一定的波动，这种波动同样会对纠斜效果产生不利影响。因此，为了更好地表征导向力的稳定性，本文选用导向力突变幅度H和波动幅值h作为导向力稳定性的评价指标：H和h越小，视为导向力在纠斜过程中越稳定，纠斜效果越好。导向力突变幅度和波动幅值与上盘阀开口角度的关系如表8所示。

表8 导向力突变幅度和波动幅值与上盘阀开口角度的关系Table 8 Relationship between abrupt transition amplitude, fluctuation amplitude of guiding force and opening angle of upper disc valve

当α=100°，200°时，在下盘阀从0°转到120°的过程中导向力突变幅度和波动幅值如图14 和图15所示。由图可知，导向力均存在突变和波动，但略有不同。当α=100°时，导向力的突变是由于巴掌伸出的数量由1个变为0个，导致推靠力直接降至0 N；当α=200°时，导向力的突变是由于巴掌同时伸出的数量由2个变为1个，突变幅度相对较小，导向力虽然发生了突变，但纠斜力并未消失，垂钻工具仍能持续进行纠斜。

图14 α=100°时导向力的突变幅度和波动幅值Fig.14 Abrupt transition amplitude, fluctuation amplitude of guiding force with α=100°

导向力突变幅度和波动幅值随上盘阀开口角度的变化曲线如图16 所示。从图16 可知，当α=180°时，导向力突变幅度和波动幅值均相对较低，推靠力较稳定。

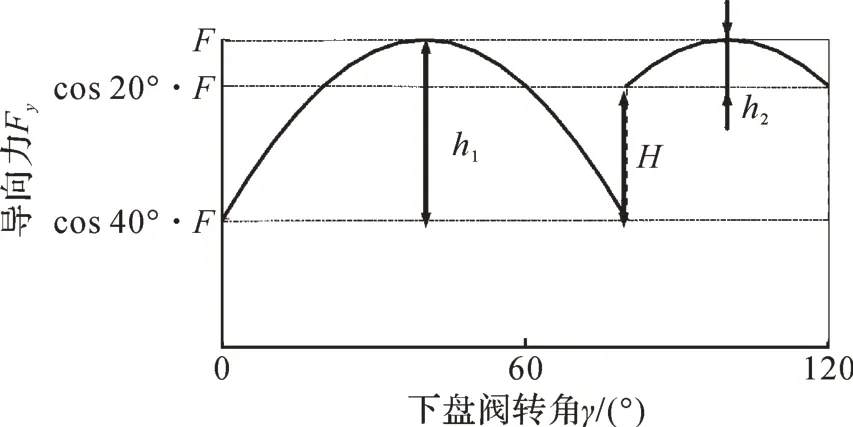
图15 α=200°时导向力的突变幅度和波动幅值Fig.16 Abrupt transition amplitude, fluctuation amplitude of guiding force with α=200°

3.4 纠斜性能评价

对扩径力冲量、导向力冲量以及导向力稳定性进行对比分析后可知：在下盘阀匀速转动的情况下，当α=180°时，扩径力冲量最小，约为0.134λ；导向力冲量最大，为6λ；导向力突变幅度最小，为0 N；导向力波动幅值最小，为0.134F。可见，当α=180°时，不仅可最大程度地避免井眼螺旋现象的发生，而且还可以保证垂直钻具持续稳定地工作，纠斜效果最好。

图16 导向力突变幅度和波动幅值随上盘阀开口角度的变化曲线Fig.16 Changing curve of abrupt transition amplitude,fluctuation amplitude of guiding force with opening angle of upper disc valve

4 结 论

机械式自动垂直钻具的纠斜性能与其上盘阀开口角度密切相关。为提高钻具的纠斜性能，保证纠斜效率，本文从纠斜原理入手，研究了钻具纠斜性能与其上盘阀开口角度的关系。研究结果表明，巴掌的运动随着上盘阀开口角度的变化而变化，在上盘阀开口角度为120°～240°时，巴掌始终伸出并推靠井壁，整个纠斜过程稳定。以扩径力冲量、导向力冲量、导向力突变幅度和波动幅值作为井眼螺旋程度、有效推靠力作用和导向力稳定性的评价指标。在上盘阀开口角度为180°时，评价指标均达到最优值，既保证了井眼质量，又能最大程度地提高纠斜效率，并使整个纠斜过程持续稳定，钻具纠斜性能最佳。