轴承钢开坯轧制温度及变形渗透性分析
2021-03-22邱军华温永红周雨辰晏安昌沈晓辉
闫 浩,邱军华,温永红,周雨辰,晏安昌,沈晓辉
(1.安徽工业大学冶金工程学院,安徽马鞍山242032;2.南京钢铁联合公司,江苏南京210035)
目前,小规格棒材生产技术比较成熟,产品质量能得到有效控制,但大规格棒材产品质量控制一直是难点,主要体现在大棒材心部质量方面。大棒材使用的坯料断面较大,受冷却影响,铸坯中心易产生较为严重的疏松和孔隙缺陷,而开坯轧制过程变形渗透性的改善有利于减轻或消除这类缺陷。受制于轧机能力及坯料尺寸,开坯轧制时的变形渗透性往往难以达到心部孔隙闭合的要求。影响大规格坯料开坯轧制过程变形渗透性的影响因素复杂,国内外研究人员为此展开了广泛研究。
洪慧平等使用LARSTRAN/SHAPE有限元模拟软件对Φ70 mm规格轴承钢棒材热轧过程进行有限元分析,验证其模型及模拟方法的正确性;张贵杰等通过三维流函数法对棒材热连轧时的椭圆-圆孔型系统进行力能参数解析,其形状函数的真实性决定了计算结果的准确度;纪树梅和黄永健等使用DEFORM有限元软件对Φ130 mm以上大规格棒材进行模拟轧制,分析影响棒材心部缺陷的因素,由此改进棒材轧制工艺;黄华贵等针对Φ150 mm大棒材连轧机组,通过数值模拟方法研究机架间张力对疏松缺陷致密压实的影响,得出采用负张力轧制比自由轧制或微张力轧制能更有效压实心部疏松缺陷;李学通等利用非线性有限元法建立孔型棒材温轧过程模型,对比分析新型孔型与传统孔型系列轧件断面塑性应变的分布规律,结果表明,使用新型孔型能较好地将变形渗透到断面中心且变形均匀,有利于心部孔隙的闭合,提高棒材质量;Wallerö等对热轧后的心部孔隙纵向压实过程进行分析,结果表明增加辊径和大压下能使变形更好地渗透孔隙部位,孔隙闭合效果得到改善;Ståhlberg等和Keife等为使孔隙闭合更好,对钢材轧制中心纵向空洞愈合时空洞周围区域的应力分布进行分析,得出了有利于空洞闭合的静水压力。
目前关于大规格轴承钢棒材的温度场研究较少,大规格棒材变形渗透与断面温度梯度的关系有待深入研究。文中针对将GCr15轴承钢320 mm×480 mm矩型坯在850粗轧机上开坯轧制成150 mm×150 mm中间坯的轧制过程,利用有限元分析软件Marc/SuperForm模拟分析轧件温度场分布及其对变形渗透性的影响,以期为改善大棒材轧制工艺制度提供理论依据。
1 有限元模拟及分析
1.1 换热系数有限元模型
轧制过程中,轧件表面换热包括轧件与周围环境的对流换热、辐射换热、轧件和轧辊孔型接触面的热传导。文中轴承钢矩型坯开坯轧制过程中的热交换包括环境温度(即空气温度)与其表面的对流换热、辐射换热和轧辊的热传导,轧件表面的辐射和对流换热可借助等效换热系数考虑,该换热系数会随轧件表面温度的变化而变化。对流换热系数H

式中:H为对流换热系数,kW/(m·K);h为工件尺寸,m;λ为介质导热率,2.32×10W/(m·K);Nu为Nusselt数。Nu 可表示为

式中:C,n为常数;Gr 为Grashof数;Pr为Prandtl数。其中,Gr 为

式中:T为坯料表面温度,K;T为环境温度,K;υ为环境介质的黏度。υ随着温度的变化而变化,表达式为

式中:θ 为边界层温度,可取坯料温度与环境温度的平均值。
Pr 也随温度的变化而变化,表达式为

C,n常数可根据Gr和Pr的乘积确定:若乘积小于10,C取0.5,n取0;若乘积在1×10~5×10之间,C取1.18,n取0.125;若乘积在5×10~2×10之间,C取0.54,n取0.25;若乘积在2×10~1×10之间,C取0.135,n取0.33。
辐射换热系数H采用牛顿冷却定律计算,表达式为

式中:ε为系统辐射率,文中取0.6;φ为角系数,取1;C为黑体辐射系数,取5.67 W/(m·K)。
故综合换热系数H的表达式为

根据式(1)~(9)作出轴承钢坯料在700~1 200 ℃时换热系数和温度的关系曲线,如图1。材料热交换高温时以空间辐射为主,低温时以对流换热为主。从图1 可得出:轧制空冷过程中辐射换热是最主要的换热模式;材料温度越高,换热系数越大。
轧辊表面温度取300 ℃,轧件与轧辊孔型接触的传热系数取10 kW/(m·K),摩擦因子取0.4,塑性变形功热转换系数设置为0.9。除鳞过程可近似看成水在冷却管中以受压流动形式均匀流过坯料表面,坯料温度高,水与坯料的换热系数取3 kW/(m·K),设置除鳞速度为0.8 m/s。

图1 空冷换热系数Fig.1 Air cooling heat transfer coefficient
1.2 有限元模型的建立与验证

表1 轧制规程Tab.1 Rolling schedule
以320 mm×480 mm的坯料为研究对象,进行9个单道次开坯轧制,将坯料轧制成180 mm×180 mm的方坯。利用有限元分析软件Marc/SuperForm 建立热-结构耦合的三维有限元模型,轧制规程如表1,轧制孔型如图2。
坯料初始温度为1 200 ℃,第一道次轧制前设置高压水除鳞,除鳞速度取0.8 m/s,水冷换热系数为3 kW/(m·K),轧制速度按照实际速度设定。为保证模拟时温度准确,在建立模型时设置实际空冷时间,道次间温度传递为下道次模型温度直接读取上道次最后一增量步节点温度,翻钢和重新划分网格的道次间温度传递利用子程序写入;模型坯料和实际坯料长度不同,模型模拟轧制时间较短,根据轧制规程计算实际轧制时间,每道次模型运行前设置空冷时长。空冷时间为上道次实际轧制时间减去模型轧制时间再加5 s,翻钢道次空冷时长多取5 s,空冷换热系数取图1换热数据。

图2 孔型Fig.2 Pass

图3 轧制有限元模型Fig.3 Finite element model for rolling
轧件模型存在对称性,按断面的1/4 进行有限元建模,结果如图3。采用单道次模拟,每两道次翻钢一次,为提高计算精度,坯料网格划分数为11 880。为防止由于大变形使网格拉长导致的计算精度降低,翻钢后重新划分网格。在划分前一道次模拟计算时,利用二次开发功能编写的子程序写出最后一增量步的模型切片横截面节点温度,在下一道次模拟划分网格后再利用子程序读入上道次记录的温度。采用热像仪拍摄轧件实际温度,再利用热像仪自带的分析软件获取坯料各位置的温度。模拟结束,对GCr15轴承钢坯料的表面温度数据进行采集处理,验证换热系数的准确性,结果如表2。

表2 轴承钢模拟表面温度与实测表面温度对比Tab.2 Comparison between simulated surface temperature and measured surface temperature of bearing steel
由表2 可见,GCr15 轴承钢模型计算的坯料表面温度与实测温度较吻合,温度误差控制在6 ℃以内。由此表明模拟计算的换热系数较准确,采用此换热系数模型模拟的温度和实测温度较为一致。
为进一步分析大规格GCr15轴承钢轧制过程中温度梯度的变化,取轧件中间切片的3个特征点A,B,C(图4(b))进行追踪分析,A点为坯料中心点,B点为表层下坯料1/4位置的特征点,C点为坯料表面特征点。各特征点的温度变化如图4。
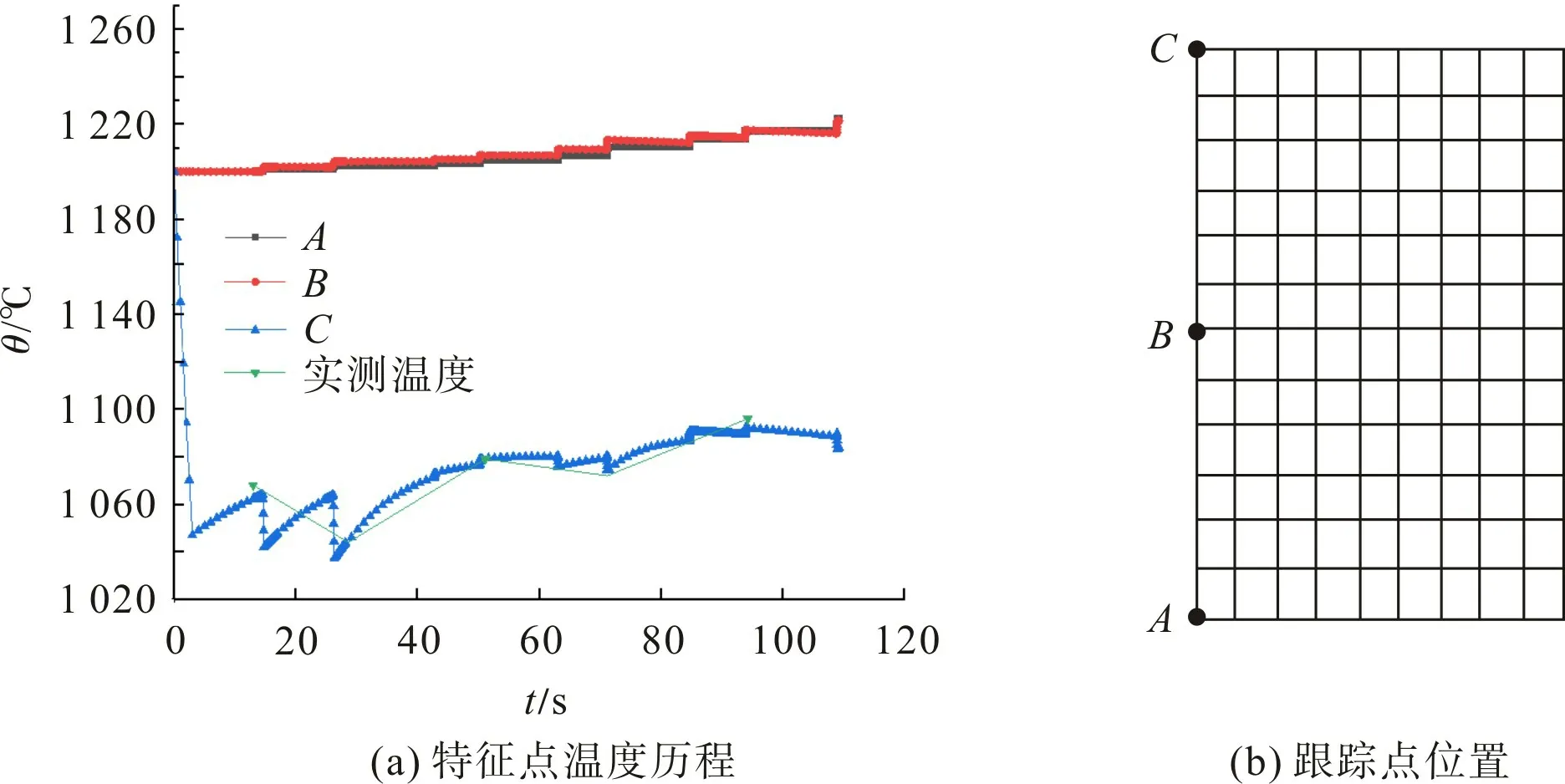
图4 轧制过程温度变化Fig.4 Temperature change during rolling
由图4可见:坯料表面特征点C在轧前高压水除鳞时温度明显下降,高压水除鳞结束,表面特征点温度为1 047 ℃,与心部特征点A温度相差153 ℃;在后续时间,轧件心表温差使其心部热量向表面扩散,致使表面温度升高。轧件接触轧辊时轧辊温度较低,导致表面温度下降,离开轧辊后心表温差大,导致轧件表面温度升高;大棒材开坯轧制过程中,心部和表面以下1/4位置温度变化不明显,总体温度变化呈上升趋势,这是由于坯料规格大、心部不易冷却、轧制速度快以及变形较大产生的热量所致。
2 温度分布对变形渗透性的影响
变形渗透性是影响大规格棒材心部质量的重要因素。为探究坯料温度分布对轧制变形渗透性的影响,文中在原有限元模型的基础上,通过变化第一道次之前的高压水除鳞速度得到不同坯料断面温度分布。将原有限元模型除鳞速度0.8 m/s 更换为0.4 m/s 和不设置高压水除鳞。不设置高压水除鳞、除鳞速度为0.8,0.4 m/s时,第1,3,5,7道次断面温度分布如图5。沿断面中心两个对称面(路径1,路径2)的温度分布曲线如图6,曲线1,2,3分别对应不设置高压水除鳞、除鳞速度为0.8,0.4 m/s时的断面温度分布。
从图5,6可看出:高压水除鳞速度越低,坯料表面冷却时间越长,表面温度越低,心部温度变化不大。一道次轧制后,轧件表面冷硬层厚度约50 mm,除鳞速度0.4 m/s 时表温度最低,约974.6 ℃,角部温度为827.5 ℃,较未除鳞冷却情况分别低184.0,268.9 ℃;随着轧制的进行,由于表面返热和变形功的影响,表面温度缓慢上升,心表温差呈减小趋势;第7道次轧制后,除鳞速度0.4 m/s情况下,轧件表面温度为1 057.4 ℃,角部温度为1 017.1 ℃,较未除鳞冷却情况分别低47.4,57.2 ℃。可见,轧前除鳞工艺对轧件表面温度及冷硬层影响显著,从而对轧件心部金属流动和变形深透性产生复杂的影响。

图5 断面温度分布Fig. 5 Distribution of section temperature


图6 断面路径的温度分布Fig.6 Distribution of temperature along the cross section path
图7为粗轧9道次后,沿断面中心两个对称面(路径1,路径2)的等效应变累积分布,曲线1,2,3分别对应不设置高压水除鳞、除鳞速度为0.8,0.4 m/s时的累积等效应变。由图7可看出:对于除鳞速度为0.4 m/s的模型,由于表面冷硬层效应最为显著,其心部累积应变最大,为1.58;对于不设置高压水除鳞的模型,心部累积应变最小,为1.53,两种情况心部等效应变相差0.05;表层等效应变分布规律与心部相反,冷硬层等效应变变化越显著、表面等效应变越小。因此,轧前除鳞冷却对轧件的变形分布均匀性影响显著,减小除鳞速度有利于改善轧件断面变形的均匀性。在轧制变形规律及表层受冷却硬化的影响下,轧件表面下1/5左右处等效应变最大。总的来看,高压水除鳞速度越低冷却时间越长,坯料断面温差越大,此时表层温度低,在压下时表层可看作硬壳,有利于心部变形的提高,对坯料心部有一定的压实效果,变形时整个断面的变形渗透会更好,对心部缺陷有改善作用。
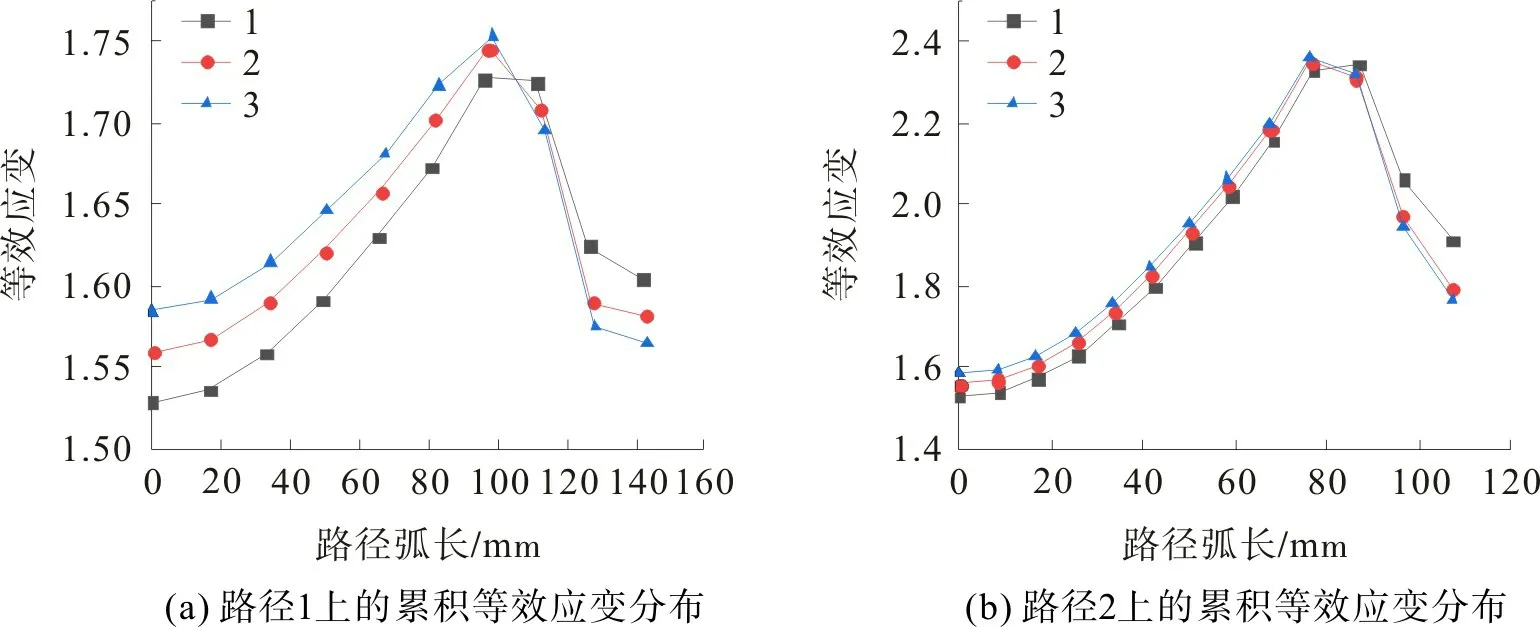
图7 断面路径上累积应变分布Fig.7 Distribution of cumulative strain along the cross section path
3 结 论
利用有限元分析软件Marc/SuperForm 建立大规格GCr15 轴承钢棒材的热-结构耦合三维有限元模型,对开坯轧制过程进行有限元模拟,分析坯料轧制过程中温度变化规律及不同除鳞条件下坯料断面温度梯度对变形渗透性的影响,得到如下结论:
1)结合现场实际测温数据验证了有限元模型的正确性,有限元模型在导入随温度不断变化的换热系数后表面温度与实测温度误差能控制在6 ℃以内;
2)开坯轧制过程中,由于高压水除磷和接触温度较低的轧辊,轧件表面温度下降、心表温差大,使心部热量向表层传递,从而使表面温度回升,但因坯料规格大、轧制速度快,心部温度降低不明显;
3)除鳞速度越慢,坯料断面温度梯度越大,变形越易渗透进坯料心部,这有利于改善大规格GCr15轴承钢的心部质量。
