浮置板轨道结构对地铁车辆轨道耦合系统动力性能影响分析*

姜朝勇 蒋咏志 宋庆伟 蔡吴斌

(1. 中车长春轨道客车股份有限公司技术中心， 130062， 长春；2. 西南交通大学牵引动力国家重点实验室， 610031， 成都∥第一作者， 正高级工程师)

浮置板轨道以其良好的减振性能在地铁系统中被广泛使用。在北京、上海、广州、杭州、西安等城市的地铁线路上有着大量的浮置板轨道。从试验和分析数据看，浮置板轨道结构可极大地改善车辆的运行性能、降低噪声[1]。此外，浮置板轨道在国外也有很多的应用案例[2-3]。

很多学者都针对浮置板的减振性能进行了研究。从建模方法上，研究浮置板的方法是构建二维或三维模型。文献[4]通过接受率法研究了在动静谐波载荷作用对非连续浮置板的影响。文献[5-7]通过傅里叶重复单元法、周期傅里叶法和修正相位法对浮置板的减振性能进行了研究。本文以北京地铁6号线车辆为样本，研究浮置板轨道对于车辆轨道耦合动力学模型的影响。

1 车辆建模

北京地铁6号线车辆转向架具有两系悬挂。二系悬挂为空气弹簧、1套抗侧滚扭杆及1套横向减振器。另外，二系还设有高度控制阀、差压阀以及非线性横向止档。一系悬挂由螺旋钢弹簧和减振器组成。该车在车体和转向架之间采用了双牵引拉杆结构。动车转向架的每根车轴都有1台交流牵引电动机。牵引电机通过弹性连接悬挂在构架横梁上，齿轮箱通过装有橡胶衬套的吊杆悬挂在构架横梁上。本文基于上述的车型特征进行建模。

2 浮置板建模

为了研究浮置板的振动，在车辆轨道耦合动力学模型中将浮置板轨道考虑成柔性体，用有限元实体单元建模，并利用模态叠加法进行求解。根据有限元理论，浮置板轨道的运动方程可以描述为：

(1)

式中：

{x}——自由度；

[M]， [C]， [K]——浮置板的质量矩阵、阻尼矩阵和刚度矩阵；

{Frs}——浮置板上扣件的作用力；

{Fp}——浮置板的底部支承力；

{FJ}——浮置板间的剪力铰提供的力。

利用模态叠加法和浮置板的正则振型函数，浮置板全局坐标的运动方程可以转换成一系列解耦的方程：

(2)

式中：

Xn——浮置板的正则坐标；

Mn，Cn，Kn——浮置板的广义正则质量矩阵、广义阻尼矩阵和广义刚度矩阵；

Pn——浮置板的广义正则载荷矩阵；

n——正则模态阶数。

3 车辆稳态响应分析

列车以100 km/h从整体道床式轨道驶入浮置板轨道时的稳态响应如图1所示。从浮置板轨道的稳态响应可以明显看出三类冲击：① 车辆从整体式道床驶入浮置板时的冲击(过渡冲击)，图中用A表示；② 浮置板之间的冲击(轨道板冲击)，图中用B表示；③ 车辆通过扣件的冲击(枕跨冲击)，图中用C表示。

图1 列车从整体道床式轨道驶入浮置板轨道的轮轨力稳态响应

由牛顿积分公式可知，轮轨力直接影响车辆的加速度，其轴箱、构架、车体的加速度稳态响应如图2所示。从图2可以看出，在轨道振动冲击自下而上的传递过程中，其影响逐渐趋于平缓。待该冲击传到车体后，加速度响应的影响主要为轨道不平顺。这证明了车辆的竖向悬挂系统能够较好地降低轮轨的冲击力。

4 不同的轨道垫板刚度对车辆系统的影响

本文对浮置板轨道采用不同的轨道垫板刚度(10～130 MN/m)时的车辆、轨道的动态响应进行分析。

轨道垫板刚度主要影响是频率在60～150 Hz范围内的振动，对低频振动的影响较小。轨道垫板的刚度越大，60～150 Hz振动处的振动越大。

轨道垫板刚度变化对轴箱振动有较大影响，轨道垫板刚度越大，轴箱振动越大。但是，由于一、二系隔离高频振动，所以对构架和车体振动影响较小。

对于轴箱和转向架来说，采用高刚度轨道垫板和低刚度轨道垫板所产生的影响差异主要是高频振动。当振动传递到车体，由于二次减振作用，两者的影响差异不大。由于影响车辆平稳性的频率范围是5～20 Hz，因而理论上可以认为轨道垫板刚度变化对车辆的平稳性影响很小。

通过安全性指标分析可以知道，轨道垫板刚度变大，轮轨垂向力和轮重减载率随之逐渐变大，但轨道垫板刚度对轮轴横向力和脱轨系数影响很小。

5 结语

本文以北京地铁6号线车辆为案例，研究了浮置板轨道对于车辆轨道耦合动力学模型的影响。建模时将浮置板轨道考虑成柔性体，用有限元实体单元建模，并利用模态叠加法进行求解。本研究分析了浮置板轨道对车辆动力学性能的影响，为轨道的选型和进一步分析车辆的动力学响应作了铺垫，同时也可为车辆轨道耦合动力学的发展提供参考。后续的研究方向应主要侧重于轨道参数的优化及轮轨接触关系的影响等方面。

a) 轴箱加速度

b) 构架加速度

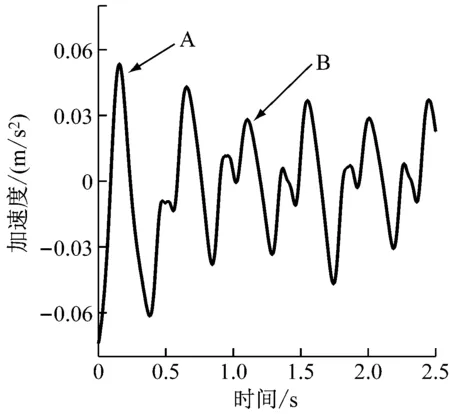
c) 车体加速度