基于弹性需求的市域轨道交通快线快慢车开行方案研究*

赵 璐 丁小兵 刘志钢 吴金龙 张 鑫

(上海工程技术大学城市轨道交通学院， 201620， 上海∥第一作者， 硕士研究生)

市域轨道交通快速线路(以下简称“市域快线”)连接市中心和郊区，其车辆一般按较高的设计速度进行配置，且部分线路在设计时预留了快车越行的条件。若采用站站停的运行模式，往往存在供需不匹配、乘客旅行时间长等缺点，设置合理的快慢车运行模式可以提高乘客的出行效益及服务质量。

相关学者对于交通方式的划分以及轨道交通线路开行快慢车开展了研究。文献[1-2]基于乘客广义出行费用构建弹性需求函数，进而建立轨道交通列车开行方案的多目标双层规划模型。文献[3]基于道路公交与轨道交通线路间形成的角度构建角度费用模型，对乘客的出行路径选择行为作了分析。文献[4]基于乘客广义出行费用建立了轨道交通市郊线路多交路快慢车双层规划模型。文献[5]分析了快慢车运行组织、客流等特点，以列车运行时间和运输成本最小为目标函数，构建了快慢车运行计划优化模型。文献[6]结合市郊客流波动大的特点，建立了包含随机机会约束的非线性市郊列车停站优化模型。而对于市域快线快慢车模式的研究多数集中于停站方案、在途时间等方面，在快慢车对其他交通方式的客流吸引方面的研究则相对较少。本文构建了出行者对于路网中交通方式选择的弹性需求函数，在分析乘客广义出行费用的基础上，建立市域快线快慢车开行方案双层规划模型。

1 问题描述

本文的研究对象为交通路网中OD(起讫点)间的2条平行线路，分别为市域快线和道路公交线路，如图1所示。市域快线为了吸引与其平行的道路公交客流，加开一定比例的快车。因此，本文讨论的是市域快线的2种列车开行方式——快车和慢车。为此，建立了仿真模型，基本假设如下：① 假定出行者可选择市域快线和道路公交2种交通方式；② 假定乘客在1次出行中只使用1种交通方式，且不考虑从出发点到O点以及D点到目的地的短距离接驳过程；③ 若选择道路公交出行，在OD间乘坐道路公交的线路可不仅限于1条；但选择轨道交通出行时，仅考虑乘坐1条市域快线的情况；④ 假定各车站站台均不存在滞留乘客的情况。

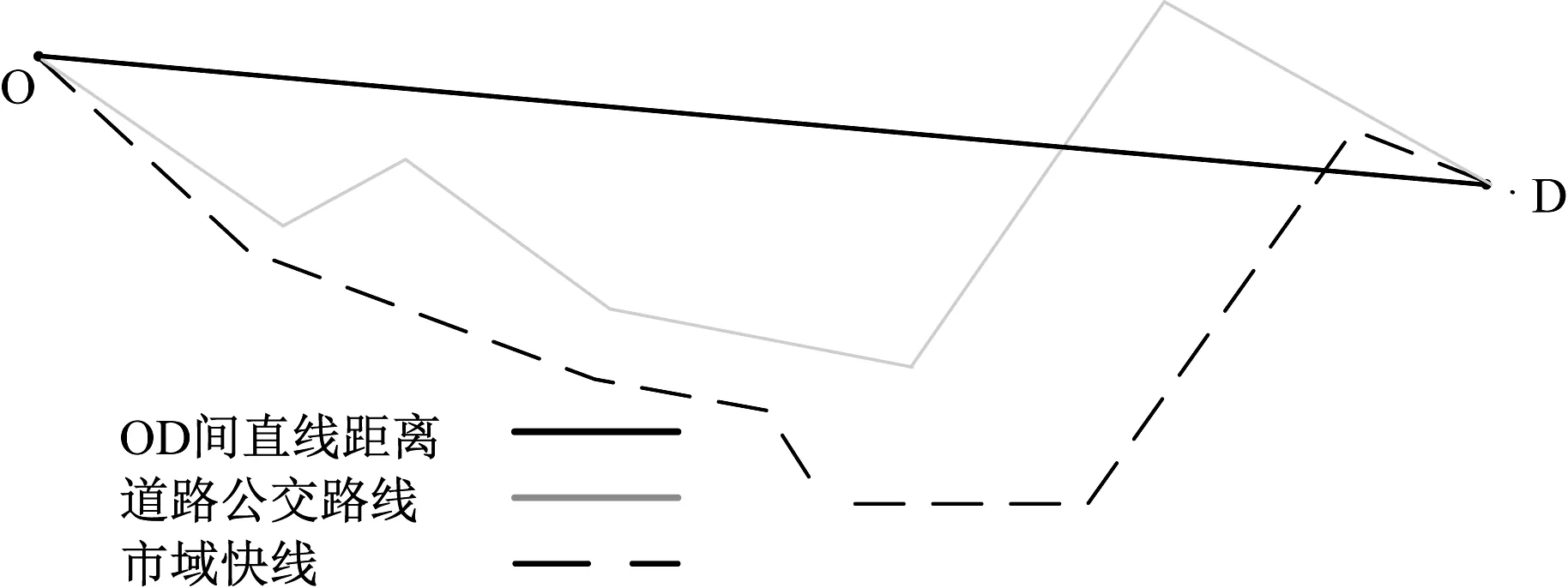
图1 OD间2种交通方式的路线示意图

2 乘客广义出行费用分析

本文将乘客广义出行费用作为出行者选择交通方式的依据。乘客广义出行费用一般包括票价费用、乘车时间、候车时间和拥挤费用4方面。

2.1 票价费用

2.1.1 乘坐市域快线的票价费用计算

轨道交通人公里票价率用ρ表示。假设从车站i到车站j的出行者fu,i,j选择市域快线，其所需支付的票价费用为：

Pu,i,j=ρωi,j

(1)

式中：

i——出行者乘坐市域快线的起点站；

j——出行者乘坐市域快线的终点站；

ωi,j——列车从车站i到车站j的运行距离；

Pu,i,j——出行者从i到j选择乘坐市域快线的k类列车所需支付的个体票价。

2.1.2 乘坐道路公交的票价费用计算

本文将道路公交线路定义为路径l。假设从车站ib到车站jb的出行者fb,ib,jb所需要支付的票价费用为：

(2)

式中：

ib——出行者乘坐道路公交线路的起点站；

jb——出行者乘坐道路公交线路的终点站；

nb——乘客在从ib到jb间乘坐道路公交经由路径l的换乘次数，次；

a——道路公交的起步票价，元；

b——道路公交的起步票价公里数，km；

x——乘客在从ib到jb间经由路径l乘坐公共汽车的乘距, km；

c——超出起步公里数外的单位加价公里数, km。

fb,ib,jb——出行者从ib到jb选择乘坐道路公交所需支付的个体票价, 元。

2.2 乘车时间

2.2.1 乘坐市域快线的乘车时间计算

乘客乘坐k类列车从车站i到车站j所需的乘车时间Tu,i,j,k为：

(3)

式中：

k——市域快线所开行的列车类别；k取1时代表快车，k取2时代表慢车；

tr——k类列车在区间(r,r+1)的纯运行时间；

tr,k——k类列车在车站r的起停附加时间；

xr,k——k类列车在车站r停站的0-1变量，停站取1，否则取0；

er,k——k类列车在车站的停站时间。

2.2.2 乘坐道路公交的乘车时间计算

乘客乘坐道路公交经由路径l从车站ib到车站jb所需的乘车时间Tb,ib,jb为：

(4)

式中：

tb——公共汽车每个区段的平均运行时间；

Dibjb,l——车站从ib到jb间乘客在路径l途径的站点个数；

Wl,m——公共汽车经由路径l在站点m的停站时间。

2.3 候车时间

2.3.1 乘坐市域快线的候车时间计算

假设乘客均匀到达车站，则乘客的平均候车时间为列车发车间隔的1/2。因此，乘客乘坐k类列车的候车时间tu,i,j,k为：

(5)

式中：

nk——k类列车在高峰小时内的开行对数，对/h；

tu,i,j,k——乘客乘坐k类列车的候车时间，min。

2.3.2 乘坐道路公交的候车时间计算

乘客选择道路公交出行时，可能会存在不同公交线路间换乘的情况，因而需要考虑换乘时间。假设乘客随机到达公交站台且发车间隔γ是常数(取值为0.5 h)，则乘客乘坐道路公交的候车时间tb,ib,jb为：

(6)

式中：

fb——公共汽车的发车频率，辆/h；

Rl——道路公交线间换乘的0-1判断函数，换乘取1，不换乘取0。

2.4 拥挤费用

2.4.1 乘坐市域快线的拥挤费用计算

拥挤费用是指由于车厢载客能力有限，使乘客感知到的拥挤度。k类列车在区间(r,r+1)的断面客流量Qu,r,k为：

(7)

式中：

s,e——k类列车运行的起点和终点；

fu,i,j,k——乘坐k类列车从车站i到车站j的乘客数量。

因此，fu,i,j,k在k类列车内的拥挤费用yu,i,j,k为：

(8)

式中：

bu——k类列车的编组辆数；

ku——k类列车的车辆定员数。

式(8)中，0.15和4是拥挤费用的无量纲经验参数[2]。

2.4.2 乘坐道路公交的拥挤费用计算

出行者在车站ib至车站jb上选择路径l的拥挤费用yb,ib,jb为：

(9)

式中：

α，χ——道路公交的乘坐舒适度参数；

qibjb,l——从ib到jb间选择路径l的客流量；

kb——路径l上的公共汽车载荷数。

2.5 广义出行费用

2.5.1 乘坐市域快线的广义出行费用计算

综合上面的计算，将乘客广义出行费用转化为货币支出形式。出行者选择k类列车的广义出行费用Cu,i,j,k为：

Cu,i,j=Pu,i,j+β[Tu,i,j,k+tu,i,j,k]+yu,i,j,k

(10)

式中：

β——乘客的平均单位时间价值。

2.5.2 乘坐道路公交的广义出行费用计算

出行者选择公共汽车的广义出行费用Cb,ib,jb为：

Cb,ib,jb=Pb,ib,jb+β[Tb,ib,jb+tb,ib,jb]+yb,ib,jb

(11)

3 模型建立及算法设计

3.1 客流分配

对于路网中多交通方式的客流分配，可由logit 模型确定：

(12)

式中：

h——交通方式种类，h取1时表示市域快线，h取2时表示道路公交；

fh——OD之间选择交通方式h的出行量；

f——OD之间的交通总出行量；

uk——市域快线中的k类列车；

τ——乘客对2种广义出行费用的理解差异度参数；

Ch——出行者选择交通方式h的广义出行费用。

3.2 模型建立

本节针对研究的问题构建双层规划，模型下层函数的解是上层函数的计算参数。

3.2.1 上层模型的建立

上层模型中建立了单目标优化模型，其约束条件主要包括列车满载率、发车间隔等，优化目标为运营效益最大。其中，运营收益来自于车票收入。运营成本G的计算如下：

(13)

式中：

cT——每列车公里的走行费用。

上层规划模型如式(15)、式(16)所示。其中：式(15)表示运营部门效益的最大化；式(16-1)表示快车的停站次数约束；式(16-2)表示列车的满载率约束；式(16-3)表示发车频率约束；式(16-4)表示列车停站的0-1约束；式(16-5)表示列车追踪间隔约束；式(16-6)表示列车的停站时间约束。

(14)

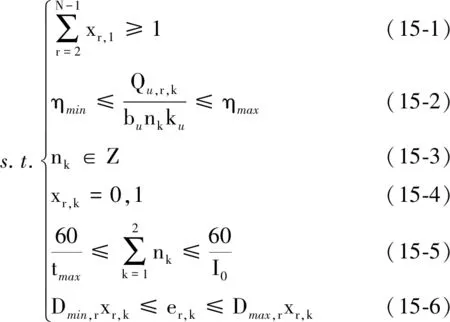
式中：

N——市域快线车站总数，个；

ηmin——列车最小满载率；

ηmax——列车最大满载率；

Z——k类列车开行对数集合；

tmax——乘客能接受的最大发车间隔，对/h；

I0——区间列车最小追踪间隔，min；

Dmin,r——列车在车站r的最小停站时间,min；

Dmax,r——列车在车站r的最大停站时间,min。

3.2.2 下层模型

出行者选择市域快线的广义出行费用如式(16)所示，选择道路公交的广义出行费用如式(17)所示。

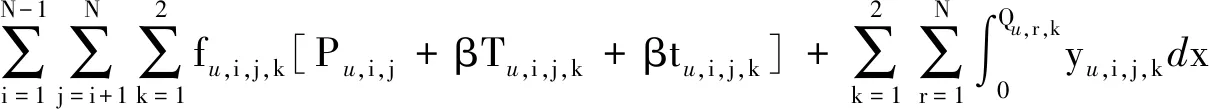
(16)

(17)

基于以上公式，建立的下层规划模型如式(18)所示。式(20)为模型的约束条件，其中：式(19-1)表示流量守恒约束；式(19-2)、(19-3)表示流量非负约束。

(18)

式中：

C——乘客广义出行费用。

3.3 求解算法

本文采用遗传算法对双层优化模型进行求解，算法过程如图2所示。

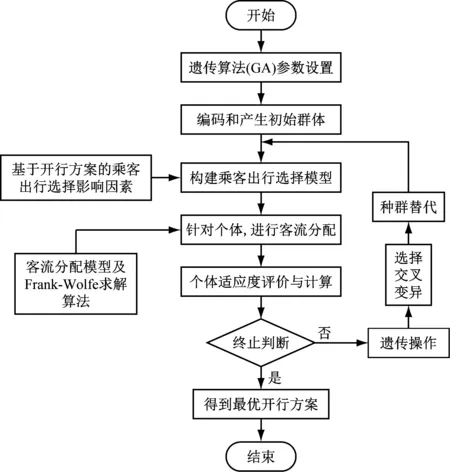
图2 采用遗传算法对模型求解的流程图

具体算法步骤如下：

1) 步骤1：设初始种群大小为M，交叉概率为Pc，变异概率为Pm，迭代次数为500次。

2) 步骤2：产生初始群体。将初始种群定义为P(k)。

3) 步骤3：构建乘客出行选择模型，并利用Frank-Wolfe算法求解下层模型。

4) 步骤4：根据客流分配情况，计算每个个体的适应度，并对其进行排序。

5) 步骤5：若最优个体在迭代500次后不再发生改变，则判断算法终止，转入步骤8；否则，转入步骤6。

6) 步骤6：遗传操作。遗传操作分为选择、交叉、变异3个过程。其中：选择是基于每个个体的适应度大小，从过渡群体中选出M个个体作为下一代群体P(k+1)；交叉是根据Pc从初始群体中选择一定的个体进行交叉，将交叉后得到的个体转到过渡群体中；变异是根据Pm从初始群体中选择一定的个体，将其基因值进行翻转，将变异后得到的个体转到过渡群体中。

7) 步骤7：种群替代。将种群P(k+1)替代P(k)，随后转入步骤3。

8) 步骤8：算法终止，得出市域快线最优的快慢车开行方案。

4 算例验证

4.1 线路概况

本文选取某中小型城市的市域快线进行研究。该线全长46.15 km，设有29座车站(1#站—29#站)，列车编组辆数为6节，设计速度80 km/h。与其平行的道路公交线路的满载定员为40 人/车，行驶速度为15 km/h，乘坐距离在10 km内每人次收费2元，超过10 km每增加5 km加价1元。市域快线和道路公交线路的站间运行时分如图3所示。客流高峰时段道路公交的发车间隔设为5 min/班，市域快线的发车间隔为6 min/列。模型其他参数设置如表1所示。

注：数字单位为s； 实线表示市域快线；虚线表示道路公交线路。

表1 模型相关参数设定值

4.2 模型求解

利用Matlab编程，并结合遗传算法对优化模型进行求解。遗传参数的设定值如下：初始群体大小为200，交叉概率Pc为0.4，变异概率Pm为0.01，迭代次数为500次。

优化前市域快线采用的是站站停的方案，经计算得到优化后的市域快线快慢车开行方案如图4所示，慢车开行频率为10 列/h，快车开行频率为2列/h，快慢车的开行比例为1∶5。

图4 市域快线开行方案优化前后对比图

在站站停模式下，慢车的单向全程运行时间为5 116 s，运营企业在高峰时段(2 h)的总运营效益为21.57万元；采用快慢车模式优化方案后，快车的单程运行时间可节约735 s，节省率约为14.37%；高峰时段客流量增加至95 553人，增长率为16.71%；企业的总运营效益可增加2.86万元，增长率为13.26%。由此可以得出结论：市域快线采用快慢车模式可较大幅度地提高中小型城市轨道交通的服务质量水平和企业运营效益。

5 结语

本文在假定交通路网中的乘客可选择道路公交和市域快线2种出行方式的基础上，分析了乘客的广义出行费用，建立了基于弹性需求的市域快线快慢车开行方案双层规划模型。采用遗传算法对该模型进行求解，获取了各类型列车的车辆编组数、停站方案、开行对数等运营组织方案。最后，以某中小型城市的某条市域快线为例进行算例分析，结果表明：相较于现有的列车开行方案，采用快慢车开行方案不仅增加了客流量，也提高了运营企业的效益。本研究可为市域快线编制开行方案提供参考。