二维修正弹修正能力建模与仿真分析
2021-03-21马景权张嘉易张云鹏于庆东郝永平
王 磊,马景权,张嘉易,张云鹏,于庆东,郝永平
(1 沈阳理工大学兵器科学与技术研究中心,沈阳 110159;2 北方华安工业集团有限公司特种弹药研究院,黑龙江齐齐哈尔 161000;3 沈阳理工大学工程实践中心,沈阳 110159)
0 引言
二维修正弹[1]是一类精确打击智能弹药,具有研发成本低、打击精度高、抗干扰性能强等优点。在常规制式弹基础上加装弹道修正机构,包括固定翼鸭舵、控制系统、GPS等。真实环境中,在风速、气压等因素的干扰下会对出膛弹丸的飞行轨迹及落点产生较大的影响。当弹丸偏离目标后,由弹载计算机解算出弹丸飞行过程中的实际弹道,通过与理论弹道比较计算出弹道偏差 ,根据偏差计算修正量,由DSP反馈至电机控制模块对电机进行调速,通过固定翼鸭舵转角对弹体进行姿态修正,达到精确打击的目的。
近年来,国内外不同研究机构对二维修正弹的修正能力研究取得一定进展。Rosales等研究了二维弹丸在阻力介质中的运动特性[2];Strub对固定翼鸭舵的风洞实验及气动仿真模型进行了研究[3];柯知非等针对弹道修正的控制特性提出了弹道修正应在上升段采取横向修正、下降段综合修正的观点[4];Wang等探究了偏航力对角运动的影响规律并进行了详细的仿真研究[5];史凯等对二维弹道修正引信的修正能力进行了评估[6]。目前研究主要问题在于:提出的大多数闭环修正算法难以直观的对修正过程进行有效复现,外界干扰条件下得到的修正时间、修正角度、修正次数等过程参数对最终落点的影响缺乏直观的仿真模型论证与分析。
针对155 mm二维修正弹,建立了闭环控制外弹道仿真模型,推导了弹体升力、导转力矩等气动力与马赫数、攻角的映射关系,利用半实物仿真平台对舵片姿态进行控制,提出了“即修即停”的修正策略,有效减轻了实弹修正过程中修正电机持续工作的负担;基于摄动落点推测[7]修正理论,所提算法考虑真实轨迹相对于理论弹道小范围波动情况,有效提高了修正精度。与传统模型相比较,根据设定的落点误差半径值及修正起始时间,对比理论弹道,计算弹道偏差进行自修正,自主计算修正次数及修停角度;算法模拟中实现了修正弹修停过程中控制、位姿等修正参数的采集与修正指标计算,在修正弹飞行过程中施加风向干扰并推导了设定修正半径与最终落点间关系。结合仿真与实验分析,进行修正过程模拟与实验结果准确度评估。
1 仿真模型修正策略
仿真模型中采用“即修即停”修正策略,飞行轨迹相对于理论弹道偏差超过阈值时,进行姿态修正;随着弹道偏差的逐步减小,实时对比理论弹道;得到的弹体位置在理论弹道的允许范围内时,完成本次修正。由于修正过程中需要精准的理论弹道作为修正输入量,为减轻弹载芯片运算负担,采用摄动落点推测法进行实时落点计算,在保证必要修正精度前提下,最大程度提高运算效率。
1.1 修正策略
弹体飞行过程中舵片状态可分为减旋、修停两类。弹丸发射后,舵片在导转力矩作用下进行快速反向旋转,为提高修正电机修停响应速度,修正算法对高速下舵片进行减速控制。对于155 mm二维修正弹,考虑修正电机能力等条件,减旋速度设定在20 r/s以下,作为弹体修正的工作条件,进行弹体修正;修停过程中对舵片姿态进行控制,在得到修停命令后,在短时间内实现舵片位置在给定角度上的保持。图1(a)为修正机构示意图,图1(b)为固定翼鸭舵舵片受力方向。

图1 二维修正机构
“即修即停”修正策略可以保证修正电机实现减旋、修停状态间切换。仿真系统以“即修即停”的修正策略为基础进行建立,整体流程图如图2。

图2 仿真模型整体流程图
首先建立固定翼鸭舵的6-D方程和理论弹道,解算各时刻飞行参数;结合摄动落点预测修正算法,根据相同射程下不同的横偏与射高值,计算修正角度、修正时间等修正参量;建立CFD计算模型获取气动参数,推导不同攻角、马赫数、高度下气动力与力矩间关系;对弹体施加气动力与力矩,将流体力学仿真结果的映射关系添加到修正弹力和力矩的计算中。通过在弹体的同向舵边缘添加标记点,测量舵片相对于弹轴方向转角与转速信息;随后将理论弹道各参数代入多体动力学模型内,编写舵片位置控制算法;根据仿真模型内标记点所获得的弹体与舵片姿态信息,计算落点误差,通过与设定偏差值对比,得到舵片修停角度及修正时间等。修正过程采用PID算法实现固定翼鸭舵在给定值上的姿态控制。
1.2 摄动理论的落点偏差推测法
弹道修正方法可分为弹道成型法、弹道追踪法与落点推测法等。摄动理论的落点偏差预测通过对速度与位置的偏导数来计算弹丸的落点偏差。理论弹道与实际弹道的弹体飞行状态可分别描述为:
E=E(x,y,z,vx,vy,vz)
(1)
E0=E0(x0,y0,z0,vx0,vy0,vz0)
(2)
式(1)中x,y,z及vx,vy,vz分别表示弹体沿理论弹道不同时刻下的位置与速度值,式(2)中x0,y0,z0及vx0,vy0,vz0表示实际弹道的各参量。
二维修正弹的理论弹道与实际弹道的飞行状态与落点可描述为:
R=f(E)
(3)
R0=f(E0)
(4)
实际弹道以时间值为基准围绕标准弹道参数摄动变化。将实际弹道在理论弹道各时刻处进行一阶泰勒展开。在满足收敛条件的情况下,将实际弹道时刻点代入得:
(5)
式中Δv,Δp表示单位时间内速度与位置的矢量变化值。最终落点偏差可分为射程偏差ΔH与横偏偏差ΔL,分别表示为:
(6)
(7)
对式(6)、式(7)中误差值求平方和,可得到误差半径。通过控制误差半径值,进行修正误差调校。
2 建立多体动力学仿真模型
2.1 气动仿真
将弹体在大气环境下受到的气动力与力矩进行流体力学仿真,获取弹体与固定翼鸭舵的气动特性。
分别对弹丸与固定翼鸭舵模型进行有限元网格划分[8];监测弹体在不同马赫数、攻角下受力情况,弹体压强分布见图3。图3中作用压强较大部分由深色显示,弹体压强主要分布于舵片底座、弹体中心及弹尾处。通过流体力学仿真,得到气动力、气动力矩与弹体马赫数、攻角、射高的关系。表1列举了部分不同马赫数与攻角下,固定翼鸭舵所受气动力矩值。

图3 弹体压强分布图
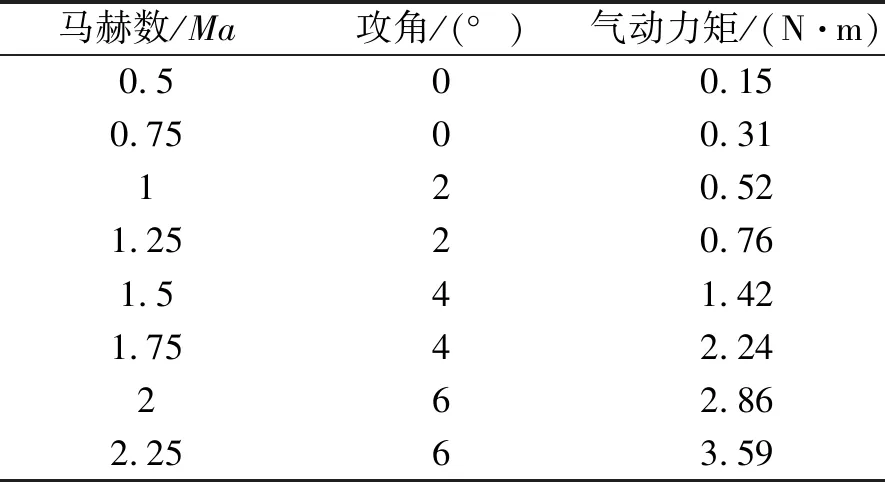
表1 部分马赫数、攻角与气动力矩对应值
将不同马赫数、攻角下的气动力、力矩进行线性拟合,得到各向气动力、力矩与攻角、马赫数之间的关系。固定翼鸭舵受到的气动力矩线性拟合结果如图4所示。

图4 马赫数、攻角与气动力矩对应值拟合结果
2.2 修正电机控制方法
修正弹内部采用修正电机连接固定翼鸭舵,如图1所示。为使固定翼鸭舵在给定位置指令下进行快速的修正动作,需要修正前对舵片进行减旋,使之稳定在可控的转速范围内。修正电机控制舵片过程采用PID算法,具体实现流程见图5。

图5 修正电机控制流程图
图5中弹体的实时飞行信息包括弹体实时速度、位置信息等,由此信息根据落点推测公式计算落点偏差。当偏差值小于设定值时,给定固定翼鸭舵的修停转速、角度,并与修正电机的反馈结果对比,形成闭环系统,实现舵片修正。
通过理论弹道计算,得到了弹体的速度、位置、姿态等解算数据,进行数据拟合,将位置、速度随时间变化的拟合结果装定到多体动力学模型中。控制模型中根据拟合结果和多体动力学模型中计算的弹体质心的实时坐标及实时速度,在采样时间内,计算弹体的位置及速度的变化值,求解速度与位置的偏导数,代入式(6)、式(7)得到实时落点位置误差半径。修正时,提前设定误差半径作为输入条件,同时根据摄动方程解算的实时落点位置误差半径进行比对与判断,当所设定误差半径大于实时误差半径,控制固定翼鸭舵按偏差值进行修停;反之,舵片保持减旋状态。
3 仿真与实验验证
仿真与实验过程以155 mm二维修正弹为对象,重点考虑施加风向干扰条件下修正偏差半径对最终落点的修正影响。
实际情况下不同高度的风速、风向错综复杂,可引入固定不变的弹道风代替实际风,且弹道风的修正量与随高度变化的实际风对弹体产生的修正量相等。利用地炮近似层权法[1],将弹道分为高度相等的6层,则第i层的层权qi的计算公式为:
(8)
根据层权可近似求得弹道风ωb为:
(9)
将弹道风施加至仿真模型,运用Adams仿真软件,为了便于分析,仿真模拟过程分别考虑了横风、纵风各自的影响,测试155 mm二维修正弹的修正效果及规律。
3.1 施加横风仿真分析
对弹体施加横向弹道风进行仿真飞行测试。分别设定落点偏差半径为3 m、5 m、10 m进行修正。设定发射初始条件如表2。
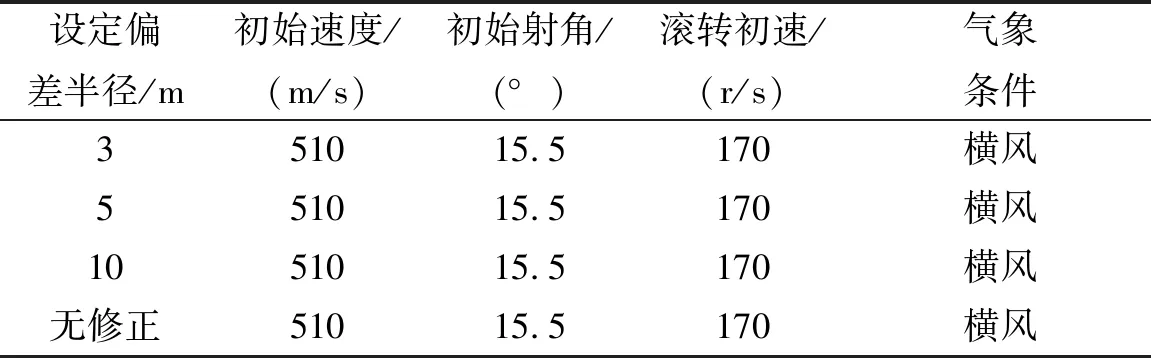
表2 发射初始条件对比
在施加横风作用下,将无修正控制的弹道、有修正控制的弹道及无风理论弹道进行对比,射程与横偏对比、射程与射高对比如图6。
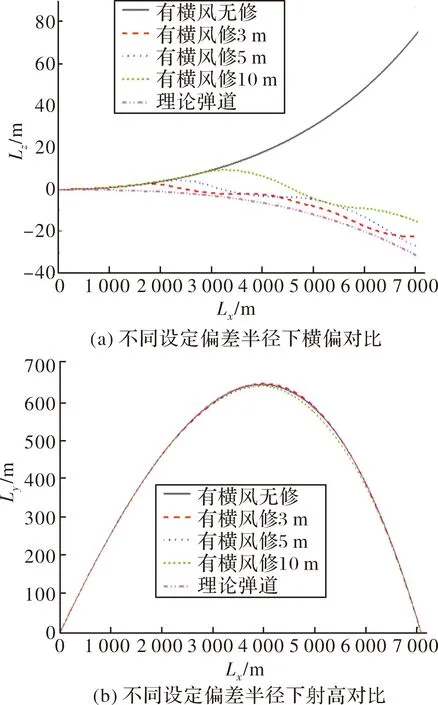
图6 横风下弹道对比
仿真中误差半径按照表2给出的设定条件,随着仿真半径的增大,弹体实时位置偏离理论弹道越大。
不同设定偏差半径下,落点参数、最大射高及误差半径对比见表3。

表3 落点参数对比
由表3可见,施加横风后,固定翼鸭舵在减旋无修正条件下横向弹体飞行轨迹受风力影响较大,产生了明显的偏差;横风对弹体射程影响不大。有修正时弹道受固定翼鸭舵同向舵的气动力影响,获得了修正效果,在设定偏差半径为3 m、5 m、10 m时,最终圆概率误差(CEP)为9.7 m、3.2 m、15.2 m,修正率为90.87%、96.99%、85.70%,修正效果理想。
3.2 施加纵风仿真分析
对弹体施加纵向弹道风进行仿真飞行测试。分别设定落点偏差半径为3 m、5 m、10 m进行修正。设定发射初始条件如表4。
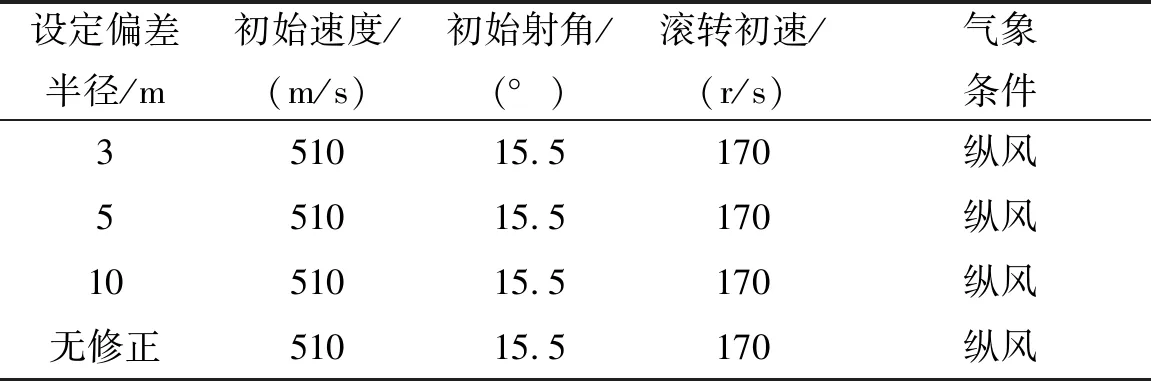
表4 发射初始条件对比
纵向弹道风作用下,无修正控制的弹道、有修正控制的弹道及无风理论弹道进行对比,射程与横偏对比、射程与射高对比如图7。

图7 纵风下弹道对比
图7表明不同误差半径条件下,仿真结果主要体现在射高、射程方向内。设定不同偏差半径的落点参数、最大射高及误差半径参数见表5。

表5 落点参数对比
纵向弹道风主要对弹丸的飞行距离产生影响,由仿真结果可以看出:在无控状态下,二维修正弹CEP为227.3 m;在施加弹道修正后,根据不同设定误差半径,修正率分别为96.05%、92.17%、93.66%,纵向修正效果符合预期。
3.3 真实打弹横向修正实验测试
以155 mm榴弹为载体进行实验,测试修正算法、修正电机响应对于舵片修停的执行效果,有风条件下预设修正偏差半径对最终落点的修正影响。因发射场地制约,选择小当量装药进行炮射实验。
实弹修正过程进行3次修正,修正角度为90°,修正时同向舵受气动力方向保持横向修正。真实修正机构舵片角度检测由霍尔传感器与一对垂直分布的单轴TMR线性磁传感器配合完成。实验中每隔1 200次霍尔信号响应进行一次定时长修正,利用地面雷达采集跟踪弹体飞行轨迹。
经计算,对于给定固定翼鸭舵相同的修正角度与修正时间时,仿真模拟结果与真实打弹有修弹落点偏差为22.11 m,达到了预期修正效果。
4 结论
通过建立二维弹道联合仿真系统,将理论弹道代入模型,根据摄动落点推测法对155 mm二维修正弹在干扰条件下进行闭环自修正。模拟求解有控二维修正弹真实发射条件下的飞行轨迹及弹道参数,得到以下研究成果:
1)弹初速510 m/s、射角15.5°初始条件,在横向风作用下,修正偏差半径设定最优值在3~8 m,修正误差可控制在90%以上;在纵向风作用下,修正偏差半径设定最优值在3 m左右,修正误差可控制在95%以上。对于不同的外界发射环境,适时调整偏差半径值及修停时间,可有效提高射击精度。
2)修正电机减旋后修正次数为3次时,可达到仿真模型内有风条件下修正要求,通过与实验结果比对,仿真模拟结果与真实打弹有修弹落点偏差为22.11 m,验证了仿真的有效性,达到了预期修正效果。
