关注概念本质,精致建构过程
2021-03-21成素华
成素华
[摘 要] 精准掌握数学概念是学生进一步学习其他数学知识的基础和前提。基于教学实践,以“周长的认识”教学为例,提出关注概念本质、精致建构过程的教学路径,使学生在丰富的体验中触及概念核心,把握概念本质。
[关键词] 周长;概念;本质;小学数学
数学概念是现实世界中物体的数量关系和空间形式本质属性的反映,它是数学知识的核心,是数学思想和方法的载体。精准掌握数学概念是学生进一步学习其他数学知识的基础和前提。在概念教学中,教师要“放慢脚步”,不能一味地追求“高效和速成”,而要追求数学概念的精致建构,让学生经历实实在在的学习过程,使学生在丰富的体验中触及概念核心,把握概念本质。
一、创设情境,激发学生的学习兴趣
新课标指出,“让学生在生动具体的情境中学习数学”“让学生在现实情境中体验和理解数学”。基于此,教师可摒弃传统教学中概念“裸现”的现象,为概念建构搭建生动的教学情境,激发学生建构数学概念的兴趣,使学生的这种内在需求在“美妙的情境”和“空旷的地带”的完美结合中自然而然地开始。
师:同学们,我们先来看一则新闻。(新闻显示:在南美洲,有一种水生植物王莲,它的叶子的周长可以达到7米,在王莲叶子上坐一个10岁的儿童也不会下沉)
生1:王莲的叶子可真大呀!
师:新闻中是如何描述王莲叶子的呢?
生2:它的叶子的周长有7米。
师:这里提到了“周长”这个概念,那么什么是周长呢?
生3:周长就是物体一周的长度。
生4:沿着王莲叶子的外围就能量出它的周长。
……
教学中,教师以“王莲叶子”的新闻方式引入周长的概念,把数学知识与学生的生活背景联系起来,激发了学生的学习兴趣,增强了学生的探究欲望,为初步理解周长的概念奠定了基础。
二、关联已知,初步理解概念
苏霍姆林斯基曾言:“教给学生能借助已有的知识去获取知识,这是最高的教学技巧之所在。”数学新旧知识之间具有密切关联,呈现出明显的螺旋式上升的趋势,由此构成了数学知识链条。在教学中,教师要结合学生的认知特点,从学生的学情出发,激活学生已有的生活经验,并加以改造、匡正和提升,借助学生的生活经验促进概念的有效建构。
师(出示王莲叶子的图片):谁能指一指王莲叶子的周长在哪里?
(两位学生上台演示。)
师:刚才,一位同学是从这个点出发又回到这个点的,而另一个同学是从那个点出发又回到那个点的,那么他们到底谁指的是王莲叶子的周长呢?
生5:都是,只要围绕王莲叶子一周,就是它的周长。
师:那我这样指可以吗?(教师指到叶子周长的一半即停止)
生6:不行,周长必须是围绕一圈的长度,这样只是围绕了半圈。
师:刚才同学们提到了两个词——“一周”“一圈”,那么到底什么是“一周”“一圈”呢?
(学生讨论。)
生7:“一周”“一圈”就是从一个点出发最后再回到这个点。
师:从起点出发回到起点,起点与终点重合,这一周的长度就是周长。
教学中,在学习周长的概念之前,学生对“一周”“一圈”有着丰富的表象认知。教师充分运用学生已有的认知经验,通过设计“指一指”数学活動,从而引导学生把周长的概念建立在“一圈的长度”“一周的长度”的知识基础上,由此延缓了学生的认知坡度,使学生初步感知了“周长”的含义。
三、数学操作,“做”中理解概念的本质
心理学家皮亚杰曾言:“活动是认识的基础,智慧从动手开始。”数学概念具有一定的抽象性,而小学生抽象思维能力薄弱,如何化解这种矛盾呢?数学操作是行之有效的办法。一是数学操作顺应了小学生性格特征。小学生在性格上活泼好动,其热衷于动手操作。在课堂教学中,教师可积极创造条件引导学生动手操作、亲身实践,调动学生的学习积极性。二是数学操作是化解概念抽象性的有效手段。操作活动使得抽象的数学概念以直观、生动、动态的形式展现出来,使得抽象的数学概念变得可感、可视,降低了学生的认知难度,为学生把握抽象概念铺就了阶梯。三是操作活动有利于把动手和动脑结合起来。“人生两个宝,双手与大脑”。教师要引导学生在探究活动中“动静结合”,在操作中思考,在思考中操作,促进操作经验和思考经验的共同发展,在“做”中理解概念的本质。
师:在生活中,除了王莲的叶子,还有很多物体都有周长。这是一片树叶,你能在黑板上描画出它的周长吗?
(一位学生把树叶贴在黑板上,然后用粉笔描画了树叶边缘一周。)
师:你还能描画出身边物体的周长吗?
生8:我用笔绕着数学书本封面的一周画了下来,就描画出了数学书本的周长。
生9:我用笔沿着铅笔盒的边缘画了一圈,就描画出了铅笔盒的周长。
……
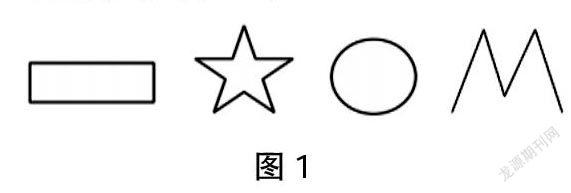
师(出示图片):请同学们尝试把这几个图形(如图1)描画在纸上,你能描画出它们的周长吗?
生10:我很顺利地描画出了前三个图形的周长,可是在描画第四个图形的周长时却遇到了问题。
师:遇到了什么问题?
生10:我发现从一点出发开始描画,却没有办法再次回到这一点,因为它“断开了”。
师:也就是说从一点开始沿着图形往前走,由于图形“断开了”,不能回到刚才那个起点了,对吗?
生10:是的。
师:那它有一周吗?
生10:没有。
师:我们把这种有缺口的图形叫作不封闭图形;把那些起点和终点重合,即首尾相连的图形叫作封闭图形。
师:非封闭图形有周长吗?
生11:没有,只有封闭图形才有周长。
教师板书:封闭图形一周的长度叫作周长。
师:你能测量出前三个图形的周长吗?
(学生讨论,并尝试测量。)
生12:长方形和五角星的边都是直直的,所以我可以用直尺把图形各个边的长度都测量出来,然后再把它们加起来,这就是这个图形的周长了。
生13:第三个图形的形状像一个鸡蛋。
师:这是椭圆,如何测量椭圆的周长呢?
生13:用直尺不能测量。
生14:可以这样做,用一段细绳绕图形一圈,然后再把绳子拉直,用尺子量一量绳子的长度,就能知道椭圆的长度了。
无论是学习经验的积累还是数学抽象能力的培养,都需要学生主动参与、积极思考和亲身实践。教学中,教师设计了丰富的数学活动,引导学生动手实践,充分调动了学生的积极性,使学生在“描一描”“辨一辨”等活动中积累了丰富的周长表征,帮助学生理解了“周长”的本质;在“量一量”的活动中进一步加深了对周长的认知,其中还渗透了“化曲为直”的数学思想。由此可见,数学操作活动不仅促进了学生对概念的理解,还丰富了学生的操作经验、探究经验和思考经验。
四、解决问题,应用中凸显概念的价值
认知心理學认为,概念的形成其实可以概括为两个阶段,即从完整表象上升为抽象概念,实现抽象概念在思维过程中的具体再现。因此,当学生获得了对概念的本质理解后,教师要及时设计综合练习,引导学生通过解决现实生活中的问题,来进一步巩固对概念的认知,彰显数学概念的应用价值。
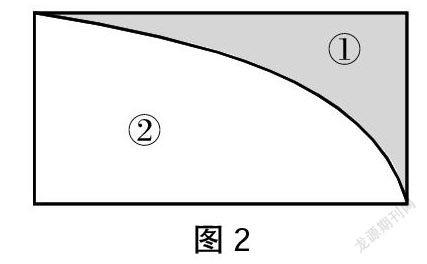
师:懒羊羊和喜羊羊分别沿着“花坛①”(图2中①号图形)和“花坛②”(图2中②号图形)的边线,同时各跑一圈,谁跑的距离更长?
生15:①号图形小,②号图形大,所以①号图形的周长比②号图形的周长短,懒羊羊跑的距离短,喜羊羊跑的距离长。
生16:不对。①号图形和②号图形的周长一样长。
师:为什么?
生16:①号图形和②号图形的周长都是两个直边加上一条曲线的长度,两个直边一样长,中间那条弯弯的曲线也是一样长的,因此①号图形和②号图形的周长一样长。
师:对。当我们比较两个图形的周长时,不能仅看哪个图形大,哪个图形小,而应该运用周长的概念进行分析、判断,这样得出的结论才是可靠的。
“纸上得来终觉浅,绝知此事要躬行”。教学中,教师引导学生运用周长的概念解决实际问题,在知识的应用中激发了学生探究的兴趣,在辨析过程中对周长的认知更加精准稳固。
周玉仁教授认为, 要为学生多创造一点思考的情境,多一点思考的时间,多一点活动的余地,多一点表现自己的机会,多一点体会成功的愉快。因此,在概念教学中,教师要有“摸着石头过河”的耐心和“打破砂锅问到底”的执着,不断细化概念教学过程,无论是概念的导入环节还是建构环节,抑或是概念的应用环节,教师都要摒弃急功近利的倾向,要给予学生充分思考的时间和空间,让概念教学精致起来!
3785500589277
