高峰时段城际铁路列车停站方案研究

张 涛，孙鹏举，曲子贤

（1.中国铁路兰州局集团有限公司 科信部，甘肃 兰州 730000；2.中国铁道科学研究院集团有限公司运输及经济研究所，北京 100081)

0 引言

城际铁路是一种区域性的轨道交通系统，主要服务于城市经济圈内中心城市、副中心城市、城市所辖城镇之间客流[1]。随着城市圈逐渐成型，城际间流动需求日益旺盛，城际高速铁路大跨度发展，并开发出刷卡进站、一站式服务、面部识别、一卡通等多种便捷服务，极大地方便了旅客出行。此外，在节假日、早晚高峰、大小长假、大型文体活动等客流激增的情况下，客流密集到站，造成车站售票厅、通道、列车等的拥挤，亟需通过优化列车停站方案等手段缓解高峰客流造成的冲击。

近年来，城际高速铁路及城市轨道交通列车开行方案优化问题成为国内外学者的研究热点。城际铁路的开行区段通常固定在发达的中心城市之间，且列车速度等级也较为单一，使得对其开行方案的优化主要集中在调整列车发车间隙、途中停站选址和编组数量等方面。Chang、Ghoneim、Liebchen、汪波等[2-5]重点研究根据客流密度情况划分城际列车运营时段问题，构建以运营成本最小化及运行时间最小化等为目标的数学模型，优化时段波动的城际列车开行方案。牛惠民等[6]通过建模研究了拥挤环境下城市轨道交通中旅客出行时间选择与列车开行方案间匹配，实现在满足旅客出行需要基础上企业利益最优的目标。史峰、彭其渊、何宇强等[7-9]将交通配流理论引入列车开行方案优化研究中，实现开行方案与客流分配的综合协调。Niu 等[10]以时间窗作为旅客乘降列车的约束，通过非线性整数规划模型优化能够满足客流动态需求的列车调度问题和开行方案问题。李得伟、邓连波、杨宏图等[11-13]分析了高速铁路停站方案的影响因素，建立非线性规划模型求解最优的列车开行方案，以满足节点服务频率、站间服务可达性、单个列车停站次数等约束条件。

分析上述文献可知，有关列车开行方案的研究大多以“按流开车”为原则，考虑在城际铁路公交化服务模式下，是否可以在客流拥挤的高峰时段满负荷地开行列车，未能兼顾不同OD 的旅客需求。城际列车在沿途中间站的停站方案会影响高峰时段的发车能力。因此，研究不同停站组合下，列车追踪间隔时间的构成，以及始发站列车发车间隔，最后建立以旅客出行时间消耗最小化为目标的非线性0-1 规划模型。

1 列车停站方案影响因素分析

1.1 列车运行和旅客出行方式

图1 1 条有m 个车站的城际铁路示意图Fig.1 Diagram of inter-city railway with m stations

假设1 条有m个车站的城际铁路示意图如图1所示，共有m个车站，从始发站1 开始，按照车站的邻接顺序依次标记为车站2，3，…，m。该线路为双向自动闭塞，即上、下行列车均有独立的运行线路。在此仅研究单向列车停站方案问题。

影响列车停站因素较多，既有列车运营因素，也有旅客选择的多样性因素。为了研究的方便，做如下假设：在高峰时段，列车在始发站和终到站间的开行数量固定，且列车的速度等级相同，相邻列车不进行越行作业。旅客到达车站后，会选择能够乘坐时间最近的列车。在以上假设条件的基础上，根据列车追踪间隔时间和不同停站组合对列车服务质量的影响2 个因素加以衡量。列车追踪间隔时间是指追踪运行的列车k与列车k+ 1 的最小间隔时间Ik，k+1。在高速铁路中，列车追踪间隔时间有：区间内追踪运行列车间隔时间t区追；前后车均到达车站停车作业的追踪列车间隔时间t停停；前后车均从车站通过的追踪列车间隔时间t通通；前车停站作业，后车通过的追踪列车间隔时间t停通；前车通过，后车到站停车作业的追踪列车间隔时间t通停；前车从车站发出，后车到达车站的间隔时间t发到；前车从车站通过后，后车从车站发出的间隔时间t通发；前车从车站发出后，后车通过车站的间隔时间t发通。通过分析，不难发现上述列车追踪间隔时间大小是不相等的。但是为了研究问题的方便，现有研究通常是按照公式(1)来确定最小追踪间隔时间[13]。

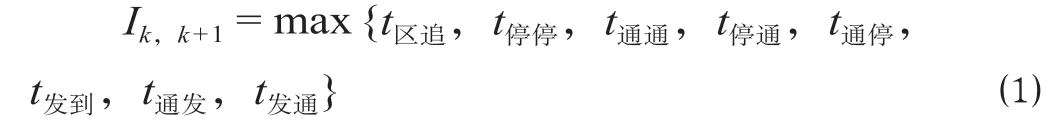
1.2 运行列车组的停站组合

在列车运行图上两相邻列车所组成的列车运行图结构单元称为运行列车组[14]。假设在划分运行列车组时只考虑列车在沿途中间站的停站组合形式。定义0-1 变量表示列车k是否在沿途中间站s停车。其中= 1 表示列车k在中间站s停车，= 0 表示列车k在中间站s通过。对于运行列车组k与k+ 1 在中间站s共有4 种停站组合形式，记做

（1）停站组合A1，1。当时，表示运行列车组k与k+ 1 均在中间站s停站作业。停站组合A1，1如图2 所示，列车k在车站s的停站时间(包括列车起、停附加时分)为t停，当列车k完成停站作业从车站s发出，且满足发到间隔时间t发到后，列车k+ 1 进入车站s。运行列车组k与k+ 1 在中间站s的最小间隔时间t1，1如公式(2)所示。

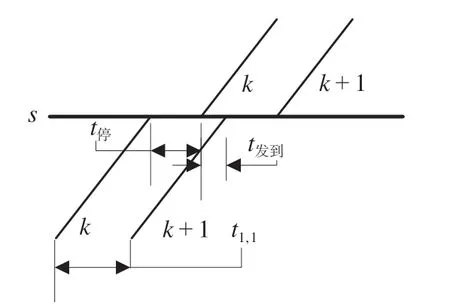
图2 停站组合A1，1Fig.2 Stop scheme of A1，1

（2）停站组合A0，0。当时表示运行列车组k与k+ 1 在中间站s均无停站作业。停站组合A0，0如图3 所示，运行列车组k与k+ 1 在中间站s的最小间隔时间t0，0需满足区间内追踪运行列车间隔时间t区追即可，如公式(3)所示。

（3）停站组合A0，1。当时，列车k在中间站s无停车通过后，列车k+ 1 到达中间站s。停站组合A0，1如图4 所示，由于列车k对列车k+ 1 无影响，运行列车组k与k+ 1 在中间站s的最小间隔时间t0，1需满足追踪运行列车通停间隔时间t区追即可，如公式(4)所示。

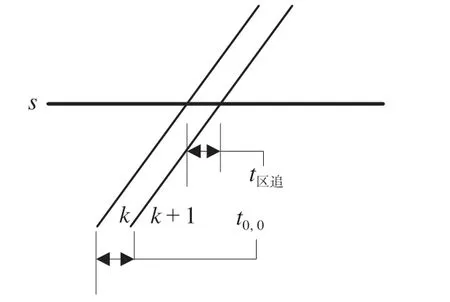
图3 停站组合A0，0Fig.3 Stop scheme of A0，0

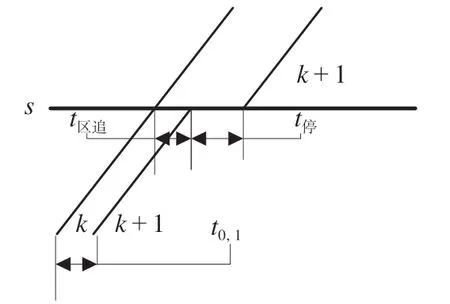
图4 停站组合A0，1Fig.4 Stop scheme of A0，1

图5 停站组合A1，0 (无越行)Fig.5 Stop scheme of A1，0 (Without overrun)

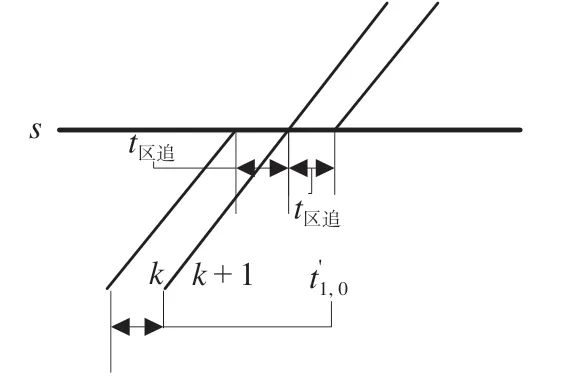
图6 停站组合A1，0 (越行)Fig.6 Stop scheme of A1，0 (Overrun)

（4）停站组合A1，0。当时，表示列车k在车站停车，列车k+ 1 通过车站。这种停站组合分为“无越行作业”和“有越行作业”2种。停站组合A1，0(无越行)如图5 所示，列车k在车站s停车作业完毕并发车后，列车k+ 1 在满足列车发通间隔时间t发通后通过中间站s。运行列车组k与k+ 1 在中间站s的最小间隔时间t1，0如公式(5)所示。停站组合A1，0(越行)如图6 所示，列车k在到达中间站s后，列车k+ 1 在满足列车到通间隔时间t到通后通过中间站s，然后列车k在满足列车通发间隔时间t通发后从中间站s发出。运行列车组k与k+ 1 在中间站s的最小间隔时间如公式(6)所示。

考虑到有越行作业时，列车k在中间站s的实际停站时间远大于其标准内停站时间t停，在构建列车停站方案模型时，不考虑有越行作业这种组合形式。

1.3 始发站列车最小发车间隔的确定

相邻列车在始发站的最小发车间隔与列车在沿途各中间站的停站组合密切相关。假设城际铁路上可办理旅客乘降的中间站集合为S∈ {s| 1，2，…，n}，则运行列车组k与k+ 1 在沿途各站的停站组合序列为其对应的运行列车组k与k+ 1 在沿途各站的最小追踪间隔时间序列为

运行列车组k与k+ 1 在始发站的最小发车间隔时间Ik，k+1应取各中间站中追踪间隔时间最大的。即Ik，k+1取值应为max {txks，xsk+1，s∈S}。在不考虑后车越行前车的情况，会出现前车停站对后车的累加影响。因此，在计算最小发车间隔时间Ik，k+1时，应考虑4 种特殊情形。

（1）A1，0与A1，0的组合。A1，0与A1，0的组合如图7 所示，当运行列车组k与k+ 1 在相邻中间站的停车组合均为A1，0时，其追踪间隔时间Ik，k+1如公式(7)所示。

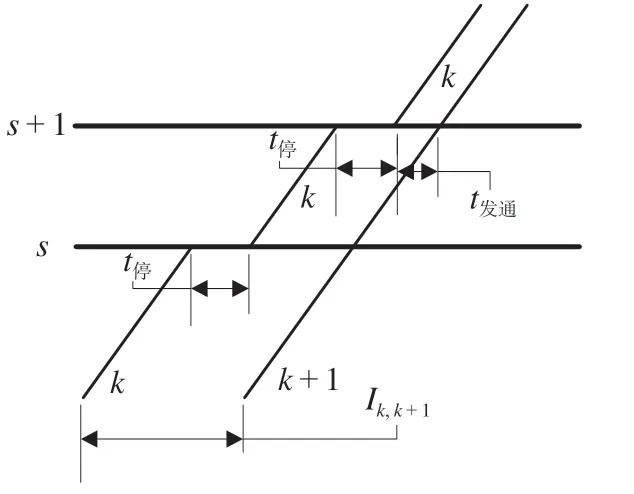
图7 A1，0 与A1，0 的组合Fig. 7 Stop scheme combination of A1，0 and A1，0

（2）A1，0与A1，1的组合。A1，0与A1，1的组合如图8 所示，当运行列车组k与k+ 1 在前、后方车站的停站组合分别为A1，0与A1，1时，其追踪间隔时间Ik，k+1如公式(8)所示，其中的max {t1，0，t1，1}取值与公式(7)类似，不再赘述。

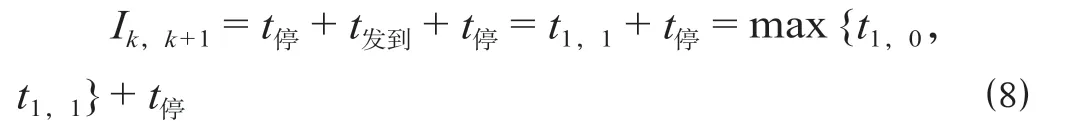
（3）A0，1与A1，0的组合。A0，1与A1，0的组合如图9 所示，当运行列车组k与k+ 1 在前、后方车站的停站组合分别为A0，1与A1，0时，其追踪间隔时间Ik，k+1如公式(9)所示。

图8 A1，0 与A1，1 的组合Fig.8 Stop scheme combination of A1，0 and A1，1

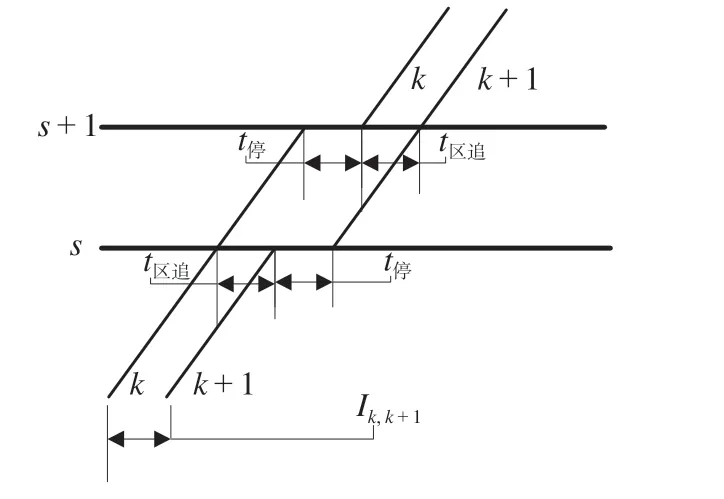
图9 A0，1 与A1，0 的组合Fig.9 Stop scheme combination of A0，1 and A1，0

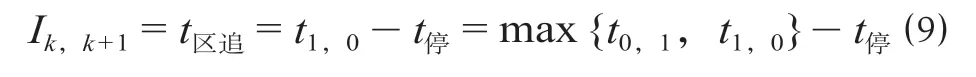
（4）A0，1与A1，1的组合。A0，1与A1，1的组合如图10 所示，当运行列车组k与k+ 1 在前、后方车站的停站组合分别为A0，1与A1，1时，其追踪间隔时间Ik，k+1如公式(10)所示。

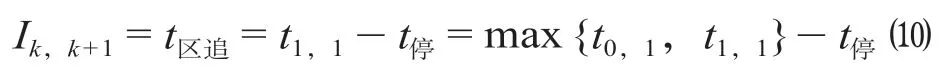
通过以上分析，可以推导出运行列车组k与k+ 1 在始发站的最小发车间隔时间Tk，k+1如公式(11)所示。

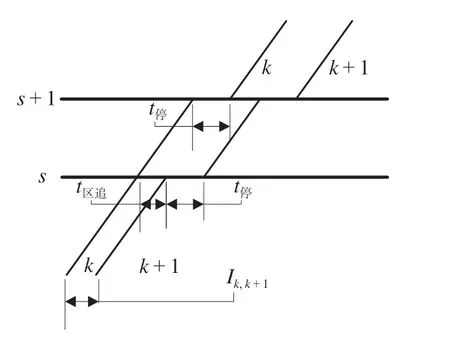
图10 A0，1 与A1，1 的组合Fig.10 Stop scheme combination of A0，1 and A1，1

2 高峰时段城际铁路列车停站方案模型构建

为保证列车在任意区间运行时均能保持最小的追踪运行间隔时间，当所有列车的停站方案均相同时，任意一对相邻列车的发车间隔时间均相等。但是，考虑到在沿途中间站乘降的旅客数量具有明显的差异性，所有列车均在沿途中间站停车会大大增加运营成本，而所有列车均不在中间站停车又无法满足旅客出行需求。因此，所构建模型需在满足旅客出行需求的基础上最小化列车停站次数，以降低运营成本。城际铁路旅客公交化出行的方式，使得旅客对列车的发车时刻较为敏感。由于不同列车停站方案带来列车发车间隔的不均衡性，必然会导致旅客候车等待时间的不均衡。另外，旅客选择不同停站方案的列车，列车停车等待时间的消耗也不均衡。为此，模型综合考虑了乘客和铁路运输企业双方利益。

2.1 目标函数

将旅客出行时间消耗最小化作为优化的目标。旅客出行时间消耗包括候车等待时间、区间运行时间和沿途停站等待时间3 部分。考虑到在城际铁路开行区段确定的情况下，相同OD 客流的区间运行时间相等。因此，只研究旅客在站候车时间和沿途停站等待时间。

设车站集合S= {s| 1，2，…，n}；中间站集合S"= {s| 2，4，…，n-1}；始发站列车的发车顺序集合K= {k| 1，2，…，m}；OD 集合V= {(i，j)|i，j∈S，i≠j；qij为高峰时段车站i→j的客流。

（1）候车等待时间。旅客候车等待时间与列车到达车站的间隔时间密切相关。列车到达车站i的时刻为。假设乘坐列车的OD 客 流qij均为时刻后服从均匀分布到达的，则OD 客流qij候车的总等待时间如公式(15)所示。

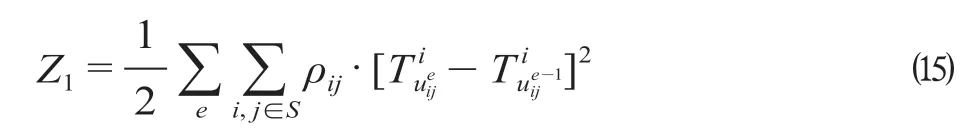
式中：ρij为客流qij的到达率参数，指车站i至车站j间每小时平均的旅客人数；ρij·表示从时刻到时刻到达车站i的客流，人；表示从时刻到达车站i的客流的总等待时间。

（2）沿途停站等待时间。对于OD 客流qij，选择乘坐列车由于列车不仅仅只服务于一个OD 客流，因而可能会产生部分旅客在沿途站等待的时间。

式中：产生停站等待时间的车站s的范围为上车站的后一站i+ 1 与下车站的前一站j- 1；ges为列车e在车站s停车后，不下车旅客的数量，人；表示在车站i至j间乘坐列车的旅客是否在s站停车等待。

通过以上分析，旅客出行时间消耗最小化的目标函数如公式(17)所示。

2.2 约束条件

（1）OD 客流qij的可达性约束。对于OD 客流qij，乘坐列车k的限制性条件为列车k的停站序列中同时包括i和j。即满足公式(18)。

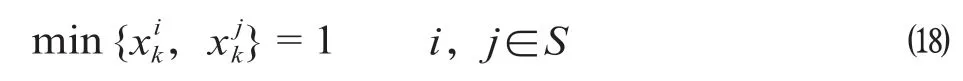
对于列车k，在停站方案∏k= {xsk，s∈S}确定的情况下，列车k可服务的OD客流可通过公式(18)确定；同时，对于OD 客流qij，其可选择乘坐列车的范围也可以通过公式(18)确定。将列车k能够服务的OD 置于集合Vk，Vk∈V；将OD 客流qij可乘坐的列车置于集合Uij= {，e= 1，2，…}，Uij∈K。

（2）客运需求与运输能力的匹配约束如公式(19)所示。

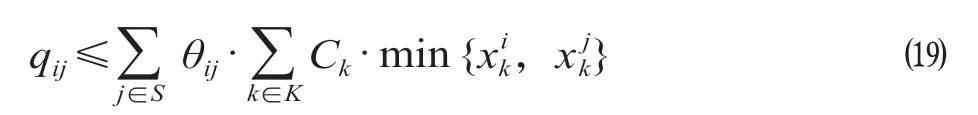
式中：Ck为列车k的定员，人；θij表示OD 客流i→j的分担率。

（3）列车到达时刻约束。在高峰时段[T高，给定第1 列车的发车时刻，按照公式(11)的推算方法，可以得到列车k在始发站的发车时间。列车k到达车站i的时刻如公式(20)所示。

式中：为区间o的列车运行时间；O为城际铁路上所有区间的集合。

（4）旅客在站候车时间约束。高峰时段旅客密集到达车站，在无法准确掌握旅客出行数量及到达规律时，通过缩小列车发车间隔，使得客流被划分为若干小单元，根据概率分布理论，在小的时间间隔内密集到达的客流可以视作服从均匀分布。因此，旅客平均等待时间即为两相邻能够服务同一OD 客流的列车到达车站i的间隔时间的一半，如公式(21)所示。

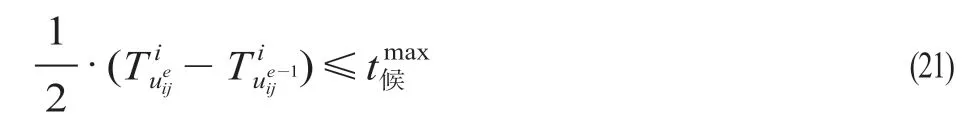
（5）到站在车无乘降旅客数量约束如公式(22)所示。

公式(22)表示，列车e在中间站a停站时，在列车上等待的旅客必须是在车站a之前的车站上车，并且在车站s之后的车站下车的乘客。

（6）高峰时段发车能力约束如公式(23)所示。

式中：f为高峰时段全部铺画平行运行图的通过能力；T高，T"高分别为高峰时段的起始时刻和终止时刻。

（7）始发、终到站强制停车约束如公式(25)所示。

3 算法设计

3.1 遗传算法

参考既有研究[15]，根据上述模型设计遗传算法计算。

（1）染色体编码。根据模型特点，设计的染色体采用0-1 编码，染色体结构如图11 所示。

图11 染色体结构Fig.11 Structure of chromosome

染色体共划分为f个基因片段，染色体长度为[(m- 2) + 1]·f。其中圆形部分表示列车k是否具有发车条件，方形部分表示列车k在沿途中间站的停站方案，为0-1 序列。当时列车k具有发车条件，圆形部分基因值为1，此时方形部分的基因取值为0 或1；当时列车k不具有发车条件，发车基因值为0，此时发车基因后的所有基因取值全部为0。染色体示意图如图12 所示。

（2）适应度函数。染色体能否被遗传到下一代取决于适应度值的大小，设计适应度函数表示为：

图12 染色体数据示意图Fig.12 Scheme of chromosome data

式中：Zmax表示最大目标函数值；Zmin表示最小目标函数值。当Z=Zmax时适应度最低为0，当Z=Zmin时适应度得到最大值为1，可见函数能够合理表达优胜劣汰的遗传原则。

（3）遗传操作。遗传操作(选择操作、交叉操作和变异操作)是遗传算法的核心步骤，通过对种群进行遗传操作可产生新一代种群。选择操作采用轮盘赌选择法，个体被遗传到下一代的概率由它的适应度与种群中所有个体适应度总和之比决定。

由于模型特点，染色体前面的基因片段会影响后面基因片段的取值。因此，在交叉和变异操作时，除了设定交叉和变异概率外，还需要增加基因位置的判断决策。变异操作如图13 所示，为变异操作的4 种情况。

当变异点被选择在“停站基因”上时(变异点1，变异点2)，首先判断变异点左侧最近的“发车基因”是否为“1”。如果“发车基因”是“1”，按照设定的变异概率Pm进行变异操作(如变异点1)，否则停止变异操作(如变异点2)。

当变异点被选择在“发车基因”上时(变异点3，变异点4)，首先判断变异点右侧最近的“发车基因”是否为“1”。如果“发车基因”是“1”，停止变异操作(如变异点3)，否则按照设定的变异概率Pm进行变异操作(如变异点4)。

3.2 算法流程

（1）初始化。按照上述染色体编码规则和约束条件(15) - (22)，随机生成规模为popsize的初始可行解种群；置最优目标Z*=M；初始开行方案WP*为零向量；方案检查集Ψ为空集；迭代次数t= 1。

（2）遗传操作。按照3.1 中设计的遗传算法，对初始种群进行选择、交叉和变异操作，搜寻当前种群中适应度最高的可行解（开行方案）WP t；迭代次数t=t+ 1。

（3）检查。如果WP t∉Ψ，那么将其添加到检查集Ψ中，转步骤（4）；否则，转步骤（2）。

（4）计算适应度。将当前开行方案WP t代入目标函数，计算目标函数Z；如果Z＜Z*，则另Z=Z*，WP*=WP t。

（5）终止检验。如果迭代次数t大于迭代上限G，输出最优解WP*，否则，转步骤（2）。

4 算例分析

以沿途有3 个中间站的城际铁路为例进行验证。列车运行参数设置如表1 所示。

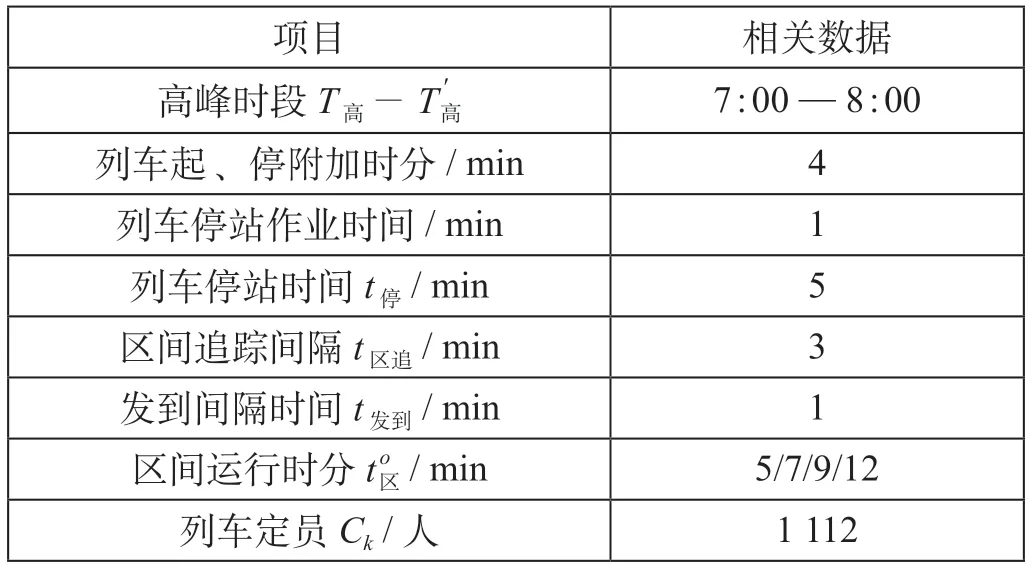
表1 列车运行参数设置Tab.1 Value of train operation parameters

客流数据参考既有文献中京津城际铁路高峰小时数据[5]，不同OD 客流的分担率及到达率如表2所示。

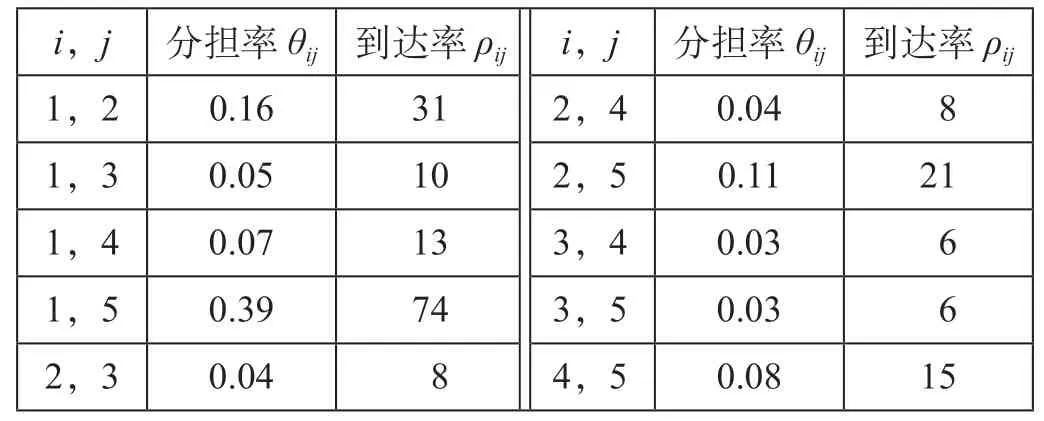
表2 不同OD 客流的分担率及到达率Tab.2 Sharing rate and arriving rate of each OD pair

图13 变异操作Fig.13 Mutation operation

将相关参数及旅客的到达率输入模型，设置种群规模popsize= 50，根据经验取交叉概率Pc= 0.6，变异概率Pm= 0.4，最大停滞迭代次数为15，最大迭代次数为100。可得到各列车发车时刻及沿途停站方案，优化后的列车停站方案如表3 所示。

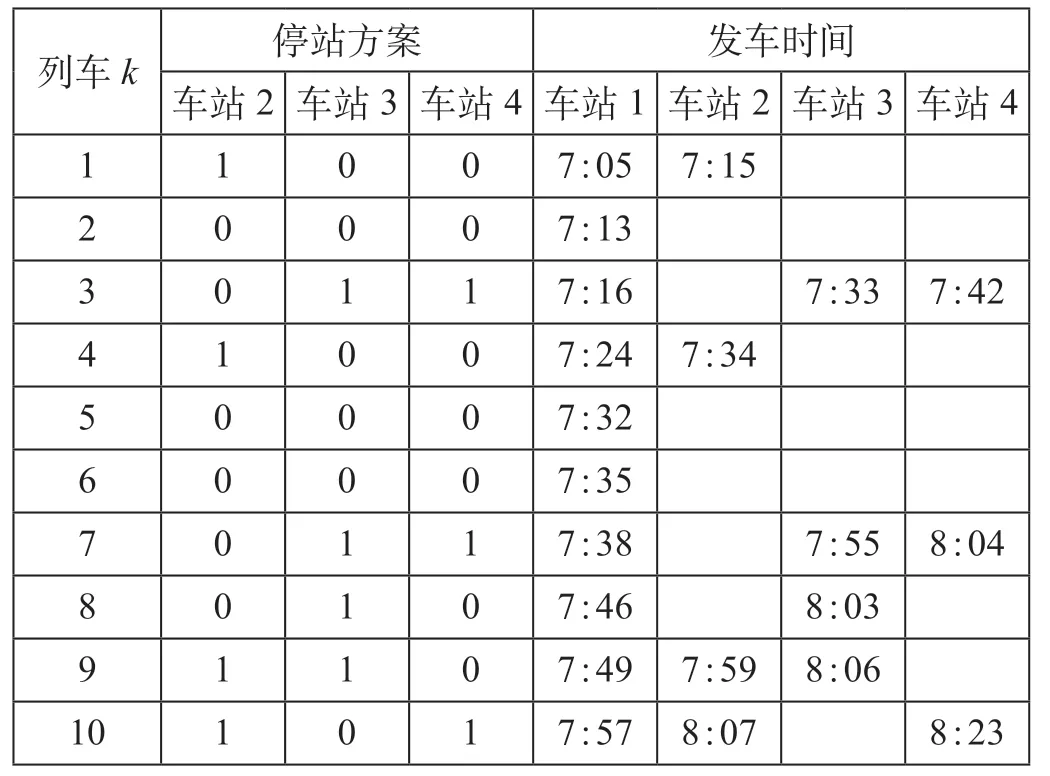
表3 优化后的列车停站方案Tab.3 Train stop scheme after optimization

表3 所示的停站方案，全部旅客在站候车时间为88 587 min，沿途停站等待时间为26 525 min，总乘车人数为8 956 人次。人均旅行时间消耗(除列车运行时分)为12.85 min，最大候车等待时间为21 min，旅客在沿途站最大停站等待时间消耗为10 min。列车最大服务能力为11 120 人次。通过以上数据，可以验证提出的模型和算法的可行性。

但是，考虑到城际铁路客运需求有动态增长的可能，在高峰时段，铁路运输企业应提供尽可能大的运输能力以满足不断增长的客运需求。通过研究发现，停站次数对通过能力的影响很大。如果在高峰时段放弃一些到达率比较低的OD 客流，减少停站次数，将会大大提高高峰小时的通过能力，同时还会降低旅客的旅行时间消耗。因此，对上述模型增加了停站次数约束，如公式(27)所示。

将相关参数及旅客的到达率输入模型，可得到各列车发车时刻及沿途停站方案，列车停站方案示意图如图14 所示。

图14 列车停站方案示意图Fig.14 Train stop scheme

该停站方案中，全部旅客在站总候车时间为49 769 min，沿途停站总等待时间为11 840 min，总乘车人数为8 079 人次。人均旅行时间消耗(除列车运行时分)为7.63 min，最大候车等待时间为21.5 min，旅客在沿途站最大停站等待时间消耗为5 min。列车最大服务能力为15 568 人次。

对比2 套方案，调整方案放弃了客流量较低的OD 客流q23，q24，q34，减少877 人次的旅客服务，使得服务能力提高了4 448 人次，旅客人均旅行时间消耗降低了5.22 min，而最大候车等待时间与原方案相当。

可见，通过优化模型进行修正后，新的停站方案在降低旅客旅行时间、提高服务能力方面得到明显改善，可以最大程度满足高峰期旅客需求激增的需要。

5 结论

通过对城际铁路客流高峰时段列车停站方案与运行图问题同步优化，在无法准确掌握旅客出行数量及到达规律时，通过缩小列车发车间隔，使得客流被划分为若干小单元，在小单元内旅客到达基本趋于均匀分布，从而客观反映实际情况。此外，城际铁路的路网结构较简单，停站数量也相对较少，以运行列车组停站组合为基础，协同优化列车开行方案与运行图，可以大大提高城际列车开行效率，提高通过能力，有效满足高峰时段激增的旅客出行需求。算例结果表明所设计的模型及算法可行，制定的列车停站方案对于后续制定城际铁路开行方案及铺画运行图可以提供有效的参考。