矩形进料体高宽比对旋流器流场和分离性能 影响的数值模拟
2021-03-20刘培坤杨兴华张悦刊
李 峰,刘培坤,杨兴华,张悦刊
(山东科技大学 机械与电子工程学院,山东青岛 266590)
0 引言
旋流器由于设计简单,占地面积小,操作方便和运营成本低,被广泛应用于选矿工业中,是一种常见的固液分离设备[1-2]。旋流器主要由进料体、圆柱段、圆锥段、溢流管和底流管五部分组成,进料流量在一定压力的作用下由进料体进入旋流器内,经过高速离心运动完成颗粒的分离,大颗粒运动到器壁,随后在重力的作用下由底流口排出,小颗粒运动到旋流器中心,由溢流管排出[3]。因此颗粒被分成两部分,从底流排出的粗颗粒和从溢流排出的细颗粒[4]。在整个输运过程中,进料体起到加速和导向的作用,因此一个好的进料体结构能提高旋流器旋流器的分离性能[5]。很多研究者对不同的进料体结构进行了探究,例如渐开线进料体,弧形进料体,同心圆进料体等[6-8]。虽然这些进料体能提高旋流器的分离效率,但是由于加工困难,转向导致的能量损失大等因素一直没有得到广泛的运用。因此采用切向进料体更具有应用价值。据报道,在不显著增加压力降的情况下,改变进料体的几何形状能提高旋流器分离效率[9]。
进料体的入口截面形状主要有圆形和矩形,其中矩形进料体应用更为广泛,前人对进料体截面为圆形进行了探究,发现进料体截面积越大,处理量越大。然而在矩形进料体当量直径不变的情况下,高宽比对旋流器分离性能的影响报道 甚少。
本文采用流体动力学(CFD)对6 种不同的高宽比(高宽比分别为0.5,0.8,1.0,2.0,3.0,4.0)矩形进料体进行了数值分析,采用RSM+VOF 模型对流场进行模拟,用RSM+Mixture 模型对颗粒分离性能进行模拟,分别从压力场、速度场、湍流场和分离效率等方面进行了探究,所得出的结论可为新型进料体的设计奠定了基础。
1 数学模型
1.1 模型描述
为了探究矩形进料体高宽比对旋流器分离性能的影响,以常规旋流器为研究基础,取高宽比分别为0.5,0.8,1.0,2.0,3.0,4.0 的6 种矩形进料体进行数值计算,常规旋流器的结构和尺寸如图1(a)所示,网格划分是数值模拟中最为重要的一步,网格的类型,数量和大小都影响数值精度,本文采用ICM 软件中O 型网格分割法将计算域划分32 万个六面体网格元素,在壁面和溢流管内部进行了网格加密,使得数值结果更加精确,如图 1(b)所示。

图1 旋流器结构参数和网格划分Fig.1 Structural parameters and mesh division of hydrocyclone
1.2 边界条件
进料口边界条件设置为速度入口,且水相和颗粒相速度均为5 m/s,溢流口和底流口设置为 压力出口,液体的黏度采用标准大气压下20 ℃时的数值,壁面采用无滑移边界条件,并且采用标准壁面函数进行近壁处理。压力-速度耦合采用SIMPLE 算法,旋流器壁面采用无滑移边界条件,压力方程采用PRESTO,动量方程采用具有三阶精度QUICK 格式,两相体积分数采用几何重建(Geo-Reconstruct)离散格式,更加准确追踪气液交界面,其余采用一阶迎风格式,在VOF 模型中底流口和溢流口处的空气回流系数设置为1,这是保证空气至少从一个口进入,瞬态模拟的时间步长设置为1×10-4s,Mixture 模型中,气泡直径设置为1×10-5mm,固体颗粒采用密度为2 673 kg/m3的石英砂为材料,进料粒度如表1 所示,以进出口流量平衡为收敛准则。

表1 进料粒度分布Tab.1 Feed size distribution
1.3 模型验证
模型验证分为两部分:水-空气和颗粒多相流。首先对水-空气多相流的情况下进行验证。1988 年,Hsieh 用LDV 对 75 mm 旋流器内部流场进行了试验探究[10],得出了详细的流场数据,该数据被很多研究者用来验证自己的物理模型。因此首先设计一个与Hsieh 完全相同的旋流器用于数据验证,CFD 与试验结果的对比如图2 所示,可以看出CFD 与试验数据有良好的吻合性,流场预测的主要偏差出现在最大值处,这主要是因为湍流模型的应用与实际产生的误差导致的,总体来说,仿真结果与试验数据基本吻合,验证了方法的有效性,因此VOF 能提供一个可靠的流场 预测。

图2 速度场试验值和模拟值比较Fig.2 Comparison of experimental and simulated values in velocity fields



图3 分离效率试验值和模拟值比较Fig.3 Comparison of experimental and simulated values of separation efficiency
2 结果分析
2.1 压力分布
旋流器是将压力能转化为动能的装置并且伴随着一定的能量损失,是颗粒分离过程中的主要动力源,图4 示出了不同高宽比时Z=205 mm 平面直径线上的压力分布。从图中可以看出,压力沿径向从壁面往中心逐渐减小,而且在箭头所示的位置,压力的变化非常急剧,几乎呈现指数形式锐减,这说明压力能转化动能的过程非常迅速。随着压力的不断减小,压力变为负值,这会使得外界的空气进入到旋流器内部形成空气柱,这也是空气柱形成的原因。随着高宽比的增加,压力先增加后减小,b/a=3.0 时,压力最大,b/a=4.0 时压力又逐渐降低。
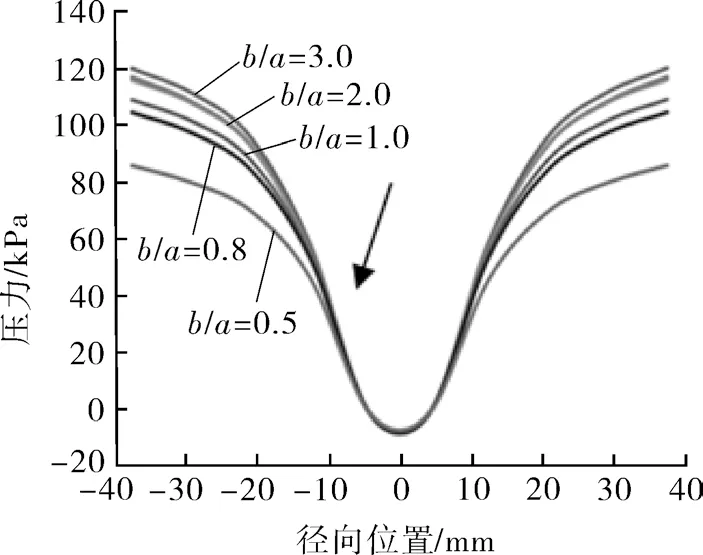
图4 不同高宽比压力比较 Fig.4 Pressure comparison at different aspect ratios
压力梯度力fΔp,i是因压力分布不均匀而作用于单位质量流体上的力,细颗粒主要受压力梯度力的影响,而压力梯度力与压力降成正比,具体表达式如下:

式中 Δp ——压力降;
Vp,i——颗粒体积。
压力梯度力的主要作用即是让细颗粒往中心运动,图5 示出了压力降随着高宽比的变化,随着高宽比的增加,压力降现增加后减小,在b/a=3.0时,压力降出现最大值,高的压力降可以使细颗粒更容易向中心运动,减少错位粒子的数量,另外图5 还显示了动态效率因子与宽高比之间的关系,动态效率因子是指总压降与动压之比,主要反映了总压降转化为动压效率大小,从图中可以看出,动态效率因子随着高宽比的增加,出现先减小后增加的趋势,在b/a=3.0 时,动态效率因子最小,这说明动压最大,能提供更大的动能。b/a=4.0 时,动态效率变大。

图5 压力降和动压效率因子Fig.5 Pressure drop and dynamic pressure efficiency
2.2 切向速度
切向速度是速度场中最为重要的速度之一,切向速度的主要作用就是产生离心力,使颗粒沿着径向分离,直接影响旋流器的分离性能,切向速度沿径向在Z=205 mm 平面处的分布如图6 所示,从图中可以看出,切向速度从壁面沿径向往中心逐渐增大,在空气柱附近最大,随后迅速降低,这符合组合涡的分布特征,这一点与压力系数的变化几乎相同。在空气柱内部,切向速度成线性降低,在中心处变为零,这表明空气柱内的气体受到的离心力非常小,因此气体在径向方向的运动几乎可以忽略。随着进料口长宽比的减小,切向速度呈现出降低的特点,切向速度的最大值出现在长宽比为3.0,当长宽比大于3.0 时,切向速度出现略微的下降,当长宽比为0.5 时,切向速度变化非常紊乱,说明流场不稳定。由于旋流器柱段部分的长宽比都大于1.0,因此为了与柱段部分有相似的高宽比形式,矩形进料体的长宽比尽量大于1.0,这有利于流场的稳定。当进料体的长宽比小于0.5时,会使流场不稳定,应避免这种情况的发生。

图6 不同高宽比的切向速度比较Fig.6 Comparison of tangential velocity at different aspect ratios
2.3 轴向速度
不同高宽比时轴向速度分布如图7 所示。

图7 轴向速度图线Fig.7 Axial velocity distribution
从图中可以看出,轴向速度分为两部分,向上流动和向下流动,向上流动是内旋流中流体的运动方向,向下流动是外旋流中流体的运动方向,外旋流的轴向速度随着宽高比没有大的变化,这说明改变进料体的宽高比对粗颗粒沿轴向运动没有太大的影响。内旋流的轴向速度在高宽比为4.0 时最大且对称性较好,高宽比为0.5 时对称性很差且没有明显的变化规律,为了提高流场的稳定性,应避免采用高宽比小于1.0 的进料体。从整体变化趋势来看,轴向速度的最大值出现在旋流器的中心处,这表明空气柱内的气体沿轴向 流动。
轴向速度不仅决定着颗粒在旋流器内的停留时间,而且还决定着分流比的大小,分流比是用底流体积流量与进口体积流量的比值来表示,理想的旋流器应该具有较小的分流比,这样会产生较少的二次液。短路流是指没有经过分离直接进入内旋流从溢流管排出,严重影响旋流器的分离精度,短路流量可以通过溢流管底端的入口流量和向下的流量差来计算,这两部分流量可以很好的被CFD-POST 软件捕捉到,计算短路流量非常方便,图8 显示了分流比和短路流量随着高宽比的变化。随着高宽比的增加,分流比呈现出逐渐降低的趋势,在b/a=2.0 时,分流比最小,高宽比继续增加,分流比逐渐变大,高宽比大于3.0 时,分流比增加幅度较大。短路流量随着高宽比的增加逐渐减小,在b/a=3.0 时短路流量最小,高宽比超过3.0 时,短路流量不增加。结合分流比和短路流量的综合分析,高宽比为3.0 时既能减小分流比又能有效的减少短路流量。
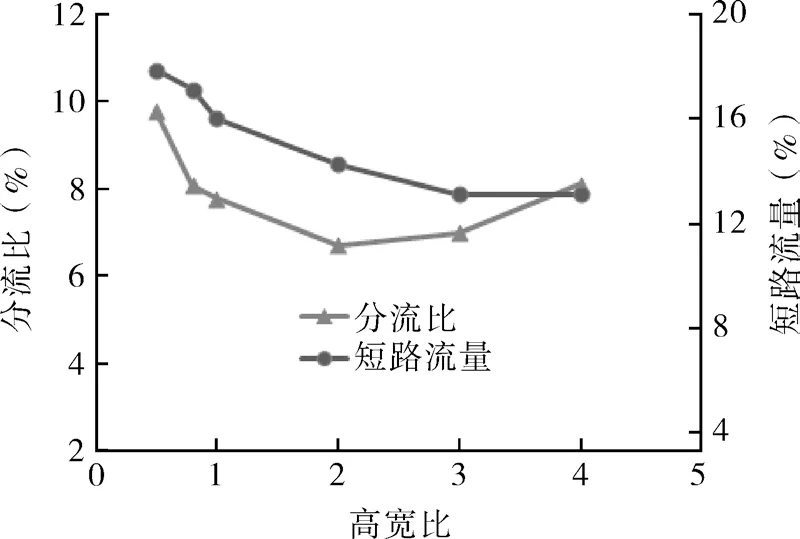
图8 短路流和分流比Fig.8 Short circuit flow and split ratio
2.4 零速包络面
轴向速度方向发生改变时,必定存在轴向速度为零的点,连接所有零点就形成零速包络面,零速包络面是内旋流与外旋流的交界面。图9 示出了不同高宽比下零速包络面的分布。中间的白色区域对于空气柱所占的面积(定义为空气体积分数大于90%的区域)。从图中可以看出零速包络面在锥段的形状成倒立的锥体,而且变化平缓,在圆柱段扭曲严重,特别是存在一些独立封闭的小圆环,这说明了循环流的存在。随着高宽比的减小,柱段内的循环流量不断增多而且扭曲严重,特别是b/a=0.5~1.0,表现最明显,少量的循环流有助于颗粒的分离,但是过多的循环流不仅会造成能量损失,而且会扰乱流场的稳定性,不利于颗粒的分离。

图9 零速包络面分布Fig.9 The LZVV distribution
零速包络面在锥段内沿轴向分布如图10 所示,当高宽比为0.5 时,零速包络面向内迁移,这使得外旋流空间更大,更多的流体进入到底流,导致分离比变大。在Z=65 mm 处出现一个峰值,该处的空气柱直径为4.3 mm,则空气柱外侧到内旋流器的距离L 非常小,这会使得细颗粒之间挤压和碰撞较为频繁,不利于细颗粒的顺利排出。因此为了让粗、细颗粒有合理的分离空间,要避免选用b/a<1.0 的进料体结构。

图10 零速包络面在锥段内分布图线Fig.10 The LZVV distribution in the cone section
2.5 湍动能
湍动能是衡量湍流发展或衰退的指标,高湍动能会增加错位粒子的数量,降低旋流器的分离性能,可以用湍流强度来估算湍动能K,计算公 式为:

式中 u ——平均速度;
I ——湍流强度。
可以看出湍动能与湍流强度成正比,理想旋流器的湍动能应该尽可能小,以减少错位粒子的数量,湍动能在Y=0 mm 平面上的空间分布云图如图11 所示,从云图中可以看出,湍动能的最大值出现在溢流管的最底端,这主要是由于该区域是多种流动交汇的区,例如短路流,强涡流,内旋流等,湍动能沿着轴向和径向逐渐降低,在边壁和锥段的下端区域湍动能最小,这主要是因为这些区域具有单一的流动性。随着宽高比的增加,湍动能逐渐减小,在b/a=3.0 时最小,在b/a=4.0 时,湍动能突然变大。

图11 湍流分布云图Fig.11 The turbulence distribution nephogram
2.6 分离性能
分离效率是评价旋流器性能指标的重要参数,宽高比对旋流器分离效率的影响如图12 所示,主要由不同粒度的颗粒在底流中的回收率组成。从图中可以看出,随着粒度的增大,底流中的回收率不断增加,这种变化趋势与旋流器的工作原理相一致,陡度指数是表征效率曲线好坏的重要指标。

图12 分离效率曲线Fig.12 The separation efficiency curve
陡度指数SI是表征分离精度高低的一个重要参考因素。
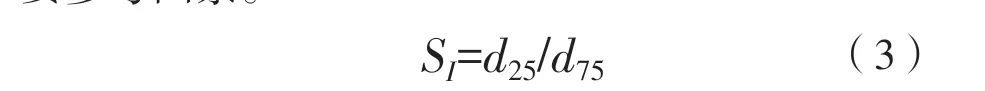
其中,d25,d75分别代表效率曲线上底流回收率为25%和75%所对应的颗粒粒度。SI的值越小,精度越高。从图13 可以看出分离精度随着宽高比的增加而增加,切割尺寸随着高宽比的增加而减小,因此适当增加高宽比可以获得更好的产品质量和较小的分割粒径。

图13 切割粒径和陡度指数Fig.13 The cutting size and steepness index
3 结论
(1)压力降和切向速度随着高宽比的增加呈现出现增加后减小的趋势,在b/a=3.0 时,达到最大,高的压力降和切向速度更容易使颗粒分离。动态系数在b/a=3.0 最小,这说明总压力降转化为更多的动压力,能量损耗最低。
(2)轴向速度没有太大的变化,但是b/a=0.5时,轴向速度变化非常紊乱,没有任何规律,这表明内部流场不稳定,应尽量避免这种情况出现,随着高宽比的增加,短路流量逐渐减小,在b/a=3.0时,短路流量最小,继续增加高宽比,短路流量没有明显改变。
(3)空气柱内部存在着压力将,很好的说明了空气柱内的气体处于流动状态。随着宽高比的增加湍动能先减小后增加,在b/a=3.0 时最小,高宽比继续增加,湍动能也逐渐变大
(4)随着高宽比的增加,分割粒径逐渐减小,分离精度逐渐增加,因此可以获得更好的产品质量,总体分析可以看出,矩形进料体最理想的高宽比应该为3.0~4.0 之间,为以后设计新型进料体提供研究方向。
