基于凸包非光滑表面的高速列车减阻技术*

朱海燕，胡华涛，尹必超，邬平波，曾 京

（1 华东交通大学 机电与车辆工程学院，南昌 330013；2 西南交通大学 牵引动力国家重点实验室，成都 610031）

随着现代高速列车的大力推广与运营，运用在高速列车领域各个方面的研究广度与深度也在不断地拓展，其中，对于高速列车的空气动力学研究也显得尤为重要。列车速度的不断提高，意味着空气动力学性能研究在列车设计领域中所占比重日益提高[1-3]，而随着速度的进一步提升，列车运行需要克服的空气阻力也会显著增加，资料表明，当列车速度达到300 km/h时，总阻力的80%来源于空气阻力[4-5]。所以研究各种实现高速列车的减阻措施显得非常重要。现阶段，对高速列车减阻的方法为优化车辆外型、优化车辆结构、改变车辆表面粗糙度等途径。早在90年代，陈南翼等人就对长度、头型方案、组成状态不同的列车缩小模型分别在变速风和变侧角风工况下做了风洞试验，总结出列头尾车形状、联挂方式、受电弓、转向架对空气阻力的影响，为后来列车减阻研究提供了重要的参考依据[6]；杨国伟等人研究对比了CRH380B和CRH3这2种车型在不同减阻措施布置情况下的减阻效果，发现相对于CRH3，改进后的CRH380B有更明显的减阻优势[7]。邵微概述了国内外高速列车头车外形的发展，利用参数化建模建立4种类型头车，并做分析对比，发现单拱型头车的减阻效果优于双拱型头车[8]；张在中则通过改变头车细长比来获取更好的减阻效果[9]；杨志刚等人发现在转向架两侧安装裙板有利于列车的减阻，并且安装位置和布置方式对列车减阻有比较大的影响，但是安装了裙板的列车在强侧风下行驶时会增加侧向力，不利于行车安全[10]；黄志祥等利用优化空调导流罩、转向架等附属设施来降低车辆的空气阻力[11]；张业等利用EMU的缩比模型，忽略门窗、受电弓的影响，研究设置不同风挡类型和不同风挡缝宽参数的动车组阻力，发现风挡缝宽对各车阻力的影响显著[12]。

Bearman、Viswanath、Efros等分别从非光滑表面运用于旋成体、面板、飞行器上，并通过试验比对，发现不同类型非光滑表面对边界层结构有直观的影响，适当形式的非光滑表面有利于减少气动阻力[13-15]。上世纪90年代末，杨弘伟和王晋军等人对边界层控制进行研究，将不同形式的非光滑表面在运用于湍流减阻上取得了良好的效果[16-17]；徐中等采用k-ε两方程模型对凹坑非光滑表面做了细致的研究，同样得到对比光滑表面，非光滑表面有着更优异的减阻性能[18]；汤勇就各种类型的非光滑表面进行了介绍，并对它们的包括脱附减阻等功能做了比较细致的综述[19]；方言后来基于仿生结构，分别将凹坑和凸包非光滑表面运用于旋成体，得到理想的减阻效果，并对二者减阻机理进行了说明[20]。

由于高速列车的快速发展，对非光滑减阻技术在高速列车运用的研究雏形渐起。林世才等以Prandtl理论为基础，建立高速列车模型，分析其边界层内部的压力和速度矢量等来研究圆坑非光滑表面对摩擦噪声的影响[21]，汪九根等从仿生学的角度出发，出于对高速列车降噪的目的，对菱形网格非光滑表面车体和koch雪花表面织构车体进行仿真试验，发现对降低摩擦噪声有显著效果[22-23]，而气动阻力和气动噪声的形成都与车体表面湍流有关，因此这也给降低摩擦阻力提供新的研究思路，为空气阻力的研究方法提供了参考依据；杜建等根据仿生学理论，提出将沟槽加设于高速列车表面，并进行模拟仿真，得到列车在高速运行时的减阻率在6%以上[24]；张渊等则提出将非光滑表面设置于车体下方的转向架前后档区域的思路，并进行验证，结果表明仅对中间车有一定的减阻效果[25]；朱海燕等通过建模和模拟仿真软件在CRH3高速列车表面加设球窝，以此来控制边界层的湍流特性，来研究列车的减阻效果，在对比不同尺寸和排列的球窝后，得出当球窝阵列距离为350 mm、半径为80 mm、深度为10 mm的时候，列车运行阻力相对最小，并且对比全光滑车面，减阻率可达25.19%，减阻效果非常显著[26]。

通过设置不同凸包参数于高速列车的非光滑表面，来研究高速列车表面的减阻效果。首先利用Pro-E软件建立在列车头车与尾车加设不同尺寸和间距的凸包的非光滑表面高速列车模型，将其导入ICEM软件进行网格划分，然后通过Fluent软件开展数值仿真计算，研究不同参数的凸包非光滑表面布置位置等对列车减阻效果的影响，获取最优的凸包参数及其在非光滑表面分布，从而为高速列车减阻设计提供新的思路与参考。

1 控制方程和数值计算

1.1 基本控制方程

按照《列车空气动力学概念》中的速度区段的划分，列车运行速度属于低速流（马赫数Ma＜0.3），除去研究两列车会车和列车过隧道2种情况，对列车进行研究时，可以按照不可压缩黏性流考虑，认为密度为常数[27]。连续方程如式（1）所示：

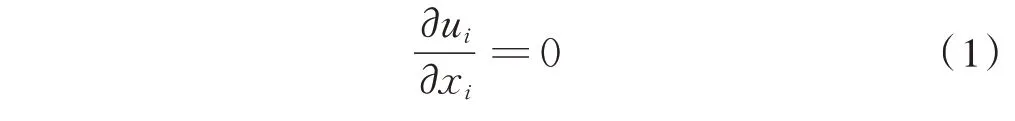
3个方向的运动方程为（2）：

式中ui或uj为流场速度；xi或xj为坐标；p为流场压力；ρ为空气密度，此处视为常量。

1.2 数值计算

由于列车有关的流动现象大部分是湍流流动，因此，在研究列车周围空气的数值模拟时，必须要讨论如何进行模拟湍流现象的问题。数值模拟湍流的方法主要有3种：直接数值模拟、大涡模拟和湍流模型，前2种由于自身的特点导致在实际应用中有很大的局限性，所以，在列车周围空气流场的湍流数值模拟领域，通常采用湍流模型[27]。而湍流模型中，涡黏性模型的应用最为广泛，k-ε两方程模型属于涡黏性模型，也在常用的湍流模型中最具代表性，能保证精度的同时，不会有过大的计算量。

k-ε湍流模型中的湍流黏性系数μt考虑了部分历史效应，把湍流黏性系数、湍流动能和湍流动能的耗散率联系在一起[28]：

湍流动能k方程为：

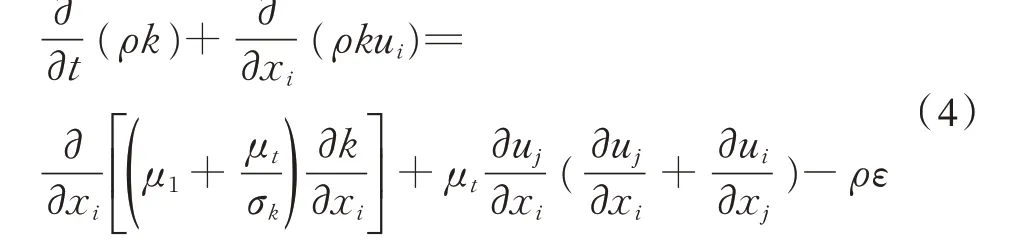
湍流耗散率ε方程为：

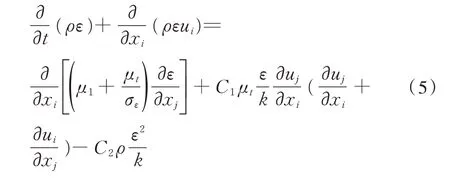
式中：μt为湍流黏性系数；k为湍流动能；μ1为层流黏性系数；C1、C2、σk、σε是经验常数，取值如下：C1=1.47，C2=1.92，σk=1.0，σε=1.33，其他参数表示为前面所述。

2 计算模型

2.1 几何模型与计算域模型

在这个分析中，选取CRH3为研究对象。首先利用三维建模软件Pro/Engineer对车体进行建模，由于在实际情况中高速动车组上有许多不平顺的地方以及车体外加设备，如：车底走行部、受电弓以及车门把手等，对这些复杂的特征进行分析会大大增加计算难度，所以将研究对象的模型简化成图1所示的一个光滑曲面体，简化后的模型理论上会得出更小的空气阻力，但对研究结果影响不大，但可以减少计算工作量，便于开展空气动力学仿真计算分析；高速列车车头处凸包表面模型如图2所示，设置不同的凸包尺寸和间距进行模拟计算。

在进行数值模拟时，为使列车周边空气流场更加接近真实工况又不过多增加计算量，选取适当的计算域是很有必要。CRH3一般采用4动4拖8节车厢的动力分散型连挂方式，由于本次只考虑非光滑表面的影响，所以模拟车辆选用3节编组的简化形式：头车+中间车+尾车，其长度均为26.5 m，并将车辆速度设置为300 km/h。参考文献[26]分析列车表面粗糙度对气动阻力影响甚微，所以将粗糙度设为0；而高速动车组尾部计算域的长度会对计算结果的精确度有较大的影响，将高速动车组放置在列车尾部距离计算域尾部175 m处，并将计算域的长设定为300 m，宽为24 m，高为36 m，整个计算域模型如图3所示。

图1 光滑表面模型

图2 车头凸包表面模型

高速列车计算域

图3 计算域模型

2.2 网格模型

几何模型导入ICEM中进行网格划分，网格采用四面体网格，密度由远场至车身逐渐增加，靠近车体表面部分是计算核心且为曲面，网格进行如图4所示的加密盒处理；另外，头车和尾车分布有凸包且为阻力集中区域，网格划分加密处理，如图5所示，且其网格尺寸是列车表面其他位置网格尺寸的五分之一，以此提高计算精度，而改变凸包参数会稍微改变网格总数量，但总数量基本维持在9.5×106左右。

图4 计算域网格模型

图5 凸包区域网格模型

2.3 边界条件

在对无横向风的高速列车运行的研究中，一般采用列车静止，让空气相对运动的方法来模拟。列车运行速度为300 km/h，故将速度入口速度设为83.33 m/s，车身视为刚体，设为固定壁面；列车在明线工况下匀速运行，将滑移壁面模拟运行时的底面、侧面和顶面，分别模拟列车在运行过程中的轨道和无穷远处的空气，采用这种移动壁面技术能够有效地避免空气附面层问题[29]，实现比较真实模拟列车运行流场，同时将中央面设为对称面以减少仿真计算量，边界条件的具体设置见表1。

3 计算结果

首先对已经建立好的模型进行2次试算来寻找是否存在规律，由于各方面原因的限制，采用固定变量法，先假设半径和凸包高度不变，参考文献[26]，尝试性计算阵列距离分别设置为160 mm和260 mm，半径为80 mm，凸包高度为20 mm的模型，与没有加设凸包的车体模型（如图6所示）进行比较，参数设置如表2所示，计算结果如图7所示。

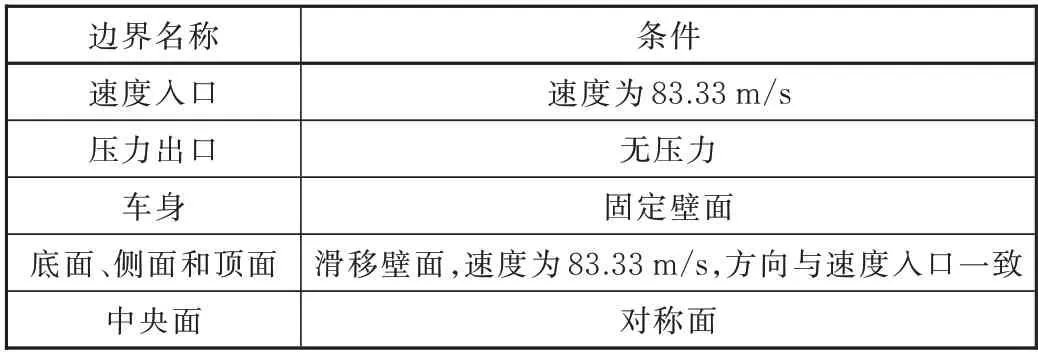
表1 边界条件

图6 凸包几何模型

表2 试对比模型代号对应参数

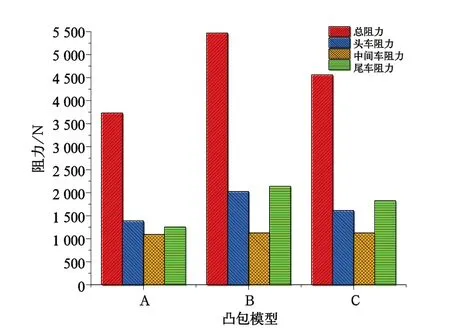
图7 试对比模型

3.1 凸包阵列距离对列车空气阻力的影响

经过数值模拟，得出光滑表面列车总阻力为3 733 N，头车阻力为1 387 N，中间车阻力为1 093 N，尾车阻力为1 253 N。经过试对比，发现非光滑表面的凸包并没有给列车带来减阻效果，相反还使得阻力值增大。而且存在凸包越密集，阻力越大的趋势。但是通过分析发现，凸包对列车外流场产生了一定的影响而且阵列距离足够大时，可以得到减阻效果。通过B、C两组数据比对后假设：在凸包半径和高度一定时，随着阵列距离的增大，头车阻力、尾车阻力以及总阻力都逐渐减小，而中间车的阻力基本不变，因此需要继续增大阵列距离并计算来观察假设是否成立，参数设置如表3所示，计算结果如图8所示。

通过观察计算结果可以发现，上述假设得到验证，在设置凸包半径和高度为不变量时，随着阵列距离增大，头车阻力、尾车阻力以及总阻力都逐渐减小，而中间车的阻力基本保持不变。在比较图8中的数据发现，当阵列距离为460 mm，凸包半径为80 mm，凸包高度为20 mm时，头车阻力为1 372 N，对比光滑表面下头车阻力略有下降。

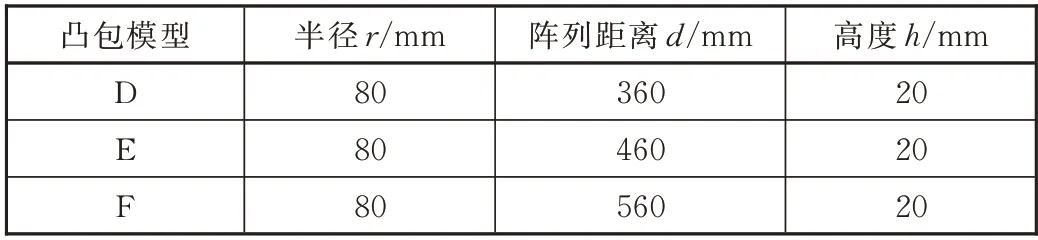
表3 阵列距离变化模型代号对应参数

图8 凸包阵列距离对列车空气阻力影响

3.2 凸包半径对列车空气阻力的影响

虽然阵列距离设置为560 mm时的尾车阻力和总阻力两项都比阵列距离设置为460 mm时的小，但分析发现，此处总阻力的减小更多源于尾车阻力较大的减小幅度，而此时尾车阻力1 405 N与光滑表面列车的尾车阻力1 253 N相比差距依然显著，故不作为后文分析参照变量，而阵列距离为460 mm时的头车阻力对比光滑表面时的头车阻力1 387 N已经出现减阻效果，且阵列距离为560 mm时的头车阻力为1 391 N，已经出现上升趋势，故此处选阵列距离为460 mm和高度为20 mm作为固定参考量，以此为基础继续使用控制变量法进一步计算分析，分别设置凸包半径为100 mm、60 mm、40 mm，具体参数设置如表4所示，计算结果如图9所示。

图9计算结果表明：总阻力、头车阻力、中间车阻力和尾车阻力都随着凸包半径的减小而减小。在凸包半径为40 mm时，各项阻力最小，总阻力为3 815 N，头车阻力为1 281 N，中间车阻力为1 101 N，尾车阻力为1 433 N，对比光滑表面各项阻力值，头车阻力下降106 N，降幅为7.64%，中间车阻力相差甚微，尾车阻力增加180 N，故总阻力依然高于同工况下的光滑表面列车。

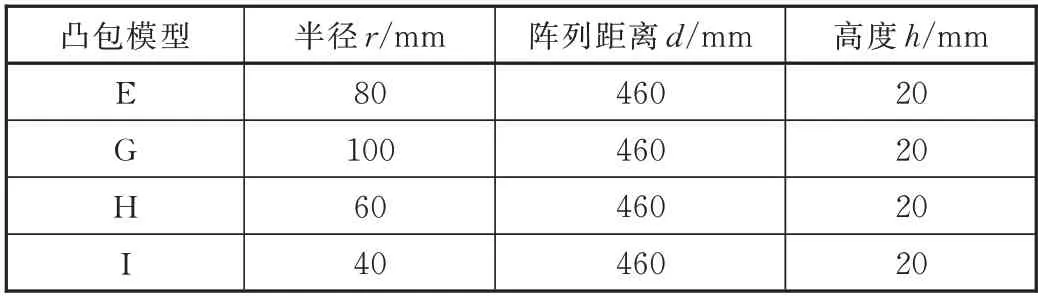
表4 半径变化凸包模型对应参数

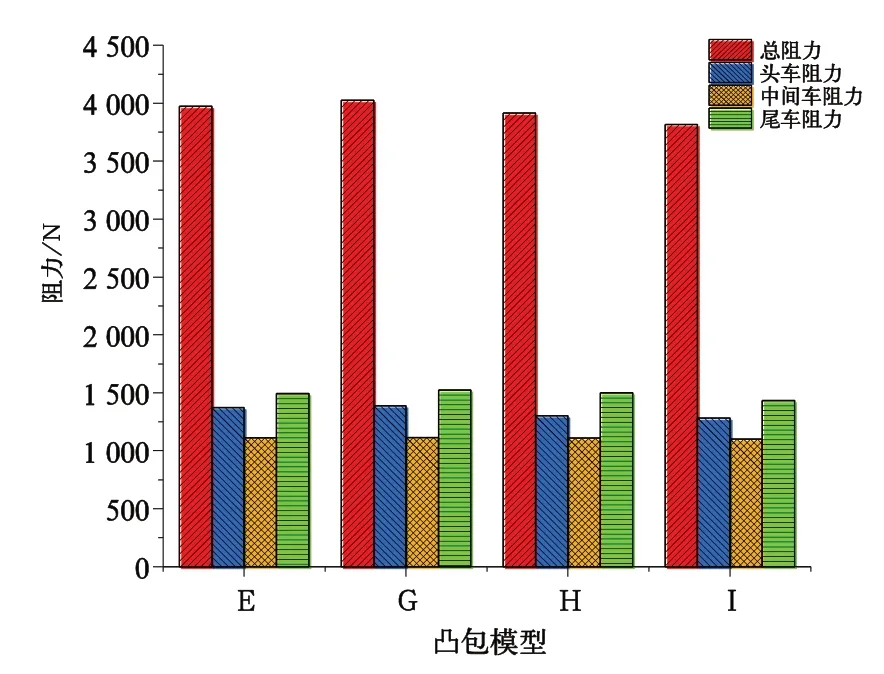
图9 凸包半径对列车空气阻力影响

3.3 凸包高度对列车空气阻力的影响

接下来选取凸包半径和阵列距离分别为40 mm和460 mm，分别设置凸包高度为20 mm、15 mm、10 mm、5 mm，具体参数设置如表5所示，得到计算结果如图10所示。

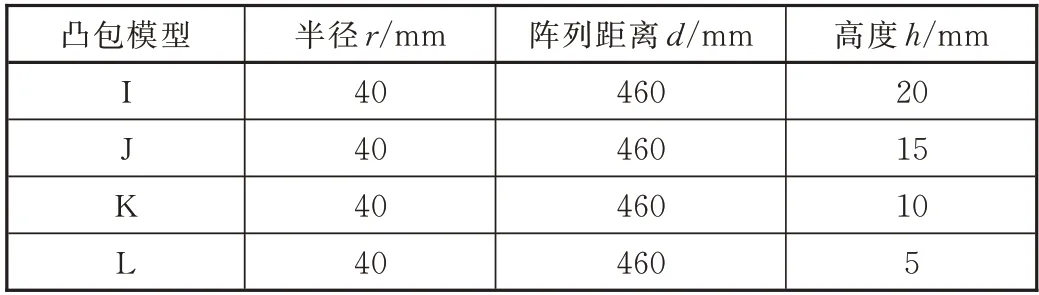
表5 高度变化模型代号对应参数

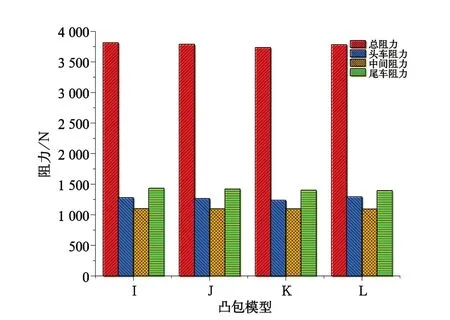
图10 凸包高度对列车空气阻力影响

分析图10可知：当凸包半径为40 mm、阵列距离为460 mm、凸包高度为10 mm时列车空气总阻力最小，为3 936 N，接近同工况下光滑表面列车总阻力，其他各项阻力值中头车阻力1 237 N、中间车阻力1 098 N、尾车阻力1 401 N，相对于光滑表面各项阻值，仅头车部分下降明显，下降150 N，头车减阻率为10.81%，出现了比较理想的减阻效果，而在凸包高度变更小时，前车阻力则有变大的趋势；中间车阻力变化不大；而尾车阻力则高居不下，依然远超全车表面光滑时尾车阻力。

基于前面分析，可知列车头部加设凸包更能体现减阻效果，而尾车阻力始终高于光滑表面列车尾车阻力，推测列车尾部加设凸包可能会增加阻力。所以接下来计算凸包模型M，即在头车加设凸包，尾车不加设凸包的工况，与之前计算的凸包模型A和凸包模型L进行比较，得到图11所示的计算结果。

图11 凸包布置方式对列车空气阻力影响

分析图11可知在尾车不设置凸包的情况下，头车阻力为1 239 N，对比光滑表面车体的头车阻力1 387 N有明显的下降，降幅达到10.7%，而中间车阻力和尾车阻力基本保持不变。凸包模型L与凸包模型M对比可以发现：尾车加设相同参数的凸包，头车和中间车的阻力几乎相等，凸包模型L的尾车阻力明显高于凸包模型M，进一步说明尾车加设凸包不利于降低列车空气阻力。

4 结果分析

上述计算结果表明：凸包加设在头车相对于加设在尾车更有利于列车的减阻，加设在尾车会起到列车增阻效果；在一定范围内，列车的气动阻力有随着凸包阵列距离的变大而减小、随着凸包半径的减小而减小、随着凸包高度的减小存在阻力先减小继而又增大的趋势；基于上述分析得到减阻效果最好的凸包参数设置为：半径40 mm，阵列距离为460 mm，凸包高度为10 mm。

空气阻力主要分为压差阻力和黏性阻力。压差阻力是列车表面压力在列车运行反方向形成的合力，而黏性阻力是列车运行中，气流在列车表面形成的切应力的合力。在高速运行的过程中，列车表面受到的黏性阻力在空气阻力占主要作用[6]。

由于空气存在可压缩性和黏性，因此高速动车组在高速行驶时，空气会在头车的车鼻处被压缩，产生极大的压力，列车头部速度矢量图12表明：在头车车鼻处周围速度很小，车鼻的速度接近为零，造成该现象的原因是列车在高速运行的时候，头车车鼻处的压力为整列车表面的最大值，列车头部压力图如13所示，根据流体的机械能守恒原理，压力极大时，此处的流体速度就会极小，而巨大的压力将空气沿着车壁往后推动，由于列车头部横截面的变化较大，空气粒子会因为巨大的压差而加速运动，所以空气粒子会在列车头部上部出现最大速度，而在此区域压力则达到最小。

图12 车头速度矢量

图13 车头压力

对于列车尾部，与上述列车头部分析方法类似，由于截面突变使得高速动车组尾部出现真空，最大截面处上方的空气粒子会向下偏转，并且压差赋予这些空气粒子产生加速度，因此在高速动车组尾部的最大截面处出现了负压，而车鼻处的空气流速快速下降，会对尾车的车鼻处产生正压，具体速度与压力分布如图14和图15所示。

稳态运行的高速列车会在车辆最前端和最尾端车鼻处产生稳定的压力，见图13和图15，头车和尾车之间纵向方向的压力合力就是压差阻力。

图14 车尾速度矢量

图15 车尾压力

列车高速运行时，空气沿列车表面做扰流运动，车壁表面附近空气的黏性力对表面存在影响，在沿壁面法向方向上存在明显的速度梯度，构成了边界层。边界层各个速度梯度的空气粒子之间存在摩擦，产生切向力，造成能量的消耗；同时，列车运行时产生的振动也会对气流产生扰动，会使边界层的结构变化，导致层流变成湍流，消耗大量的能量，这2个耗能的过程构成黏性阻力。当高速气流流过车体表面时，会对凸包产生正压力，气流流经凸包后存在回旋运动，会在凸包的背风侧产生反压力，正、反压力之差即为气流对凸包的真实作用力，一般情况下，该作用力对凸包的压力数值都是正值，即在列车运行过程中对凸包存在空气阻力，而气流对多个凸包总的作用力对车辆产生比较显著的增阻效果，因此，凸包的存在对车辆的压差阻力是有增加效果。

研究中发现并非所有的凸包加设在头车或尾车上都能起到减阻效果，因为减阻效果的出现是必须具备压差阻力和黏性阻力合力减小的条件。凸包的存在改变了气流黏性底层的结构，使得空气流动变成雷诺应力的流动，而靠近列车表面区域的雷诺应力很小，因此凸包非光滑表面黏性阻力相对光滑表面有所减小。结合图16和图17分析可知：相对于光滑表面，近壁区的湍流强度在凸包非光滑表面会明显减少，说明雷诺应力会显著减小，同时表示黏性阻力会变小。

图18和图19为光滑表面车体和凸包非光滑表面车体的湍流动能对比，经分析可知：光滑表面湍流动能最大的区域在头车的车鼻区域，而凸包非光滑表面列车则将这一区域转移至凸包分布区域，这是造成空气阻力变化的原因之一，但由于尾车凸包的存在，增加了整车表面耗能区域面积，所以尾车不加设凸包时减阻效果更好。

凸包非光滑表面加设在头车部分，增加了车辆的压差阻力，但是有效地减小了车辆的黏性阻力，不同参数、不同布置方式的凸包结构会对高速列车的压差阻力和黏性阻力都产生影响，而把合适参数的凸包加设在车辆的合适位置会使黏性阻力的下降量高于压差阻力的提升量，使得总的空气阻力下降，达到减阻效果。

图17 非光滑表面湍流强度

图18 光滑表面湍流动能

图19 非光滑表面湍流动能

5 结束语

在理论分析基础上，通过数值计算对凸包非光滑表面高速列车减阻技术进行研究，以凸包的参数、布置方式和位置为变量，分析了凸包对于高速列车气动阻力的影响，并得到较好的减阻效果，具体结论如下：

（1）由于凸包非光滑表面结构气动性能的特殊性，相比于在尾车或头车和尾车均加设凸包非光滑表面，在尾车加设凸包非光滑表面不利于高速列车减阻，仅在头车加设凸包更加有利于高速列车的减阻。

（2）凸包表面减阻效果受凸包的高度、阵列间距及半径的影响。一定范围内列车的气动阻力有随着凸包阵列距离的变大、凸包半径的减小而减小，随着高度的减小而先减小后增加；当凸包半径为40 mm、阵列间距为460 mm、凸包高度为10 mm时，头车减阻效果最好；对比光滑表面列车受到的列车阻力，仅在头车加设凸包的非光滑表面列车头车减阻率高达10.67%，总减阻率可达3.80%。

（3）由于本次模拟仿真采用简化模型，势必会导致总阻力偏小，因此此次的研究为定性研究，理论上得到减阻率会稍偏大，但可以确定凸包型非光滑表面能减少黏性阻力，对减阻产生积极效果，后续研究中要继续完善模型，期待得到更准确的分析结果。