基于AFSA的动车组制动计算研究*
2021-03-20李中奇邢月霜
李中奇,邢月霜
(1 江西省先进控制与优化重点实验室,南昌 330013;2 华东交通大学 电气与自动化工程学院,南昌 330013)
动车组制动能力的好坏反映制动系统的性能优劣,直接影响列车的行车安全。近年来随着列车速度不断增大,旅客对乘坐的舒适度有了较高要求[1-2],动车组的制动系统也受到严峻考验,因此研究动车组制动计算已然成为国内外众多学者研究的重要课题。
目前国内动车组的关键制动技术之一是采用制动减速度控制模式[3],但由于动车组制动过程较为复杂,制动计算中的制动减速度、单位制动力、基本阻力等核心参数无法精准确定,不能直接套用既有公式进行计算。针对动车组制动计算,文献[4]在进行紧急制动距离计算时,详细阐述并给出了其按速度分段的理由。但计算过程中速度段分隔过大,导致计算结果产生很大误差。为了减小制动计算过程带来的误差,文献[5]分析了列车的制动原理,提出动车组制动计算的积分方法。该方法在制动计算精度方面有了很大提高,但在求解列车积分原函数的过程中较为繁琐复杂。文献[6]指出在实际工程应用计算中,某些核心计算的积分在求解原函数过程中存在一定的复杂性。文献[7]阐述了传统的数值积分大都是基于等距节点分割求和的求积公式,要想得到较高的精度必须需要更多的节点。针对动车组在实际过程的变减速运动,考虑到动车组近似计算法精度不高及制动积分法求解原函数的复杂性问题,从智能算法的角度进一步对动车组制动计算问题进行分析讨论。近年来,随着群智能算法的发展和普及,国外学者Ne⁃shaat[8]等对人工鱼群算法进行了综述,指出人工鱼群算法具备收敛快、精度高等优点。该算法能够有效地克服局部极值达到全局极值最优的目的,在组合优化问题[9]以及电力故障检测[10]等诸多应用问题中呈现出良好的实用性。
以动车组制动距离和制动时间为研究目标,提出不等距离分割与人工鱼群结合的方法优化动车组制动计算。该方法的提出不仅是对动车组制动计算方法的补充,更是对传统数值积分方法的改进,从而为动车组制动系统的设计提供参考依据。
1 有效制动计算的数学模型
动车组制动距离主要包括有效制动距离和空走距离。动车组空走距离Sk由牵规中既有公式可得,见式(1)。主要是对有效制动计算进行建模和数据仿真验证。

式中:v0为制动初速度,km⋅h-1;tk为制动空走时间,s。
1.1 有效制动计算参数
动车组目前的制动方式采用微机控制综合制动,已经没有普通列车中换算制动率、闸片换算摩擦系数等概念[11],需要利用动车组的目标减速度、单位基本阻力、回转质量系数等核心参数建立动车组有效制动计算的数学模型。
根据运动学知识,减速距离S和减速度a存在式(2)关系:

由式(2)可看出,制动减速度是动车组有效制动距离计算的重要参数。通过查阅制动系统的设计资料,得出在每个速度间隔内制动目标减速度a的表达式为式(3):

式中:k、q为关于速度v一次函数的系数,k的不同取值代表列车不同的运行状态。若k=0,表示列车做匀减速运动;若k≠0,表示列车做变减速运动。
目标减速度以式(3)的形式给出,并结合系统给定的制动级位和动车质量进行制动力计算[12]。因此单位制动力b可由制动系统引发产生,表示为式(4):
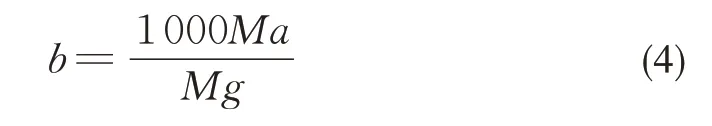
式中:M为动车质量,kg;a为制动目标减速度,m⋅s-2;g≈9.81 m⋅s-2。
将式(3)代入式(4)得到的单位制动力b与速度v的表达式为式(5):

此外,列车在实际运行制动过程中,会受到基本的运行阻力,对制动过程造成很大的影响[13]。经过大量研究实验推导出单位基本阻力ω0的公式[14-15]为式(6):

式中:v表示列车当前运行速度,km⋅h-1;A、B、C为式(6)二次函数的常数,其值由试验确定且随动车类型变化而变化;基本阻力的单位为N⋅kN-1。
1.2 有效制动计算优化函数的建立
对于列车的制动过程而言,可将整个列车视为一个刚性系统,其动能的减少量等于作用于该列车总制动力所做的功[16]。因此根据运动学中的动能定理可以推导出列车在任意速度间隔[v1,v2]内的有效制动距离Δs和有效制动时间Δt的微分方程为式(7)和式(8):

式中:v1、v2表示任意速度间隔的初速和末速,km⋅h-1;t1、t2表示v1、v2所对应的时间s;γ表示回转质量系数;g≈9.81 m⋅s-2;b表示动车单位制动力,N⋅kN-1;ω0表示动车单位基本阻力N⋅kN-1;ij表示行驶坡道单位阻力(本文取ij=0),N⋅kN-1。
式(7)和式(8)是关于b和ω0的积分方程表达式,现将式(5)和式(6)代入式(7)中,可整理出任意速度间隔内有效制动距离积分公式如式(9):
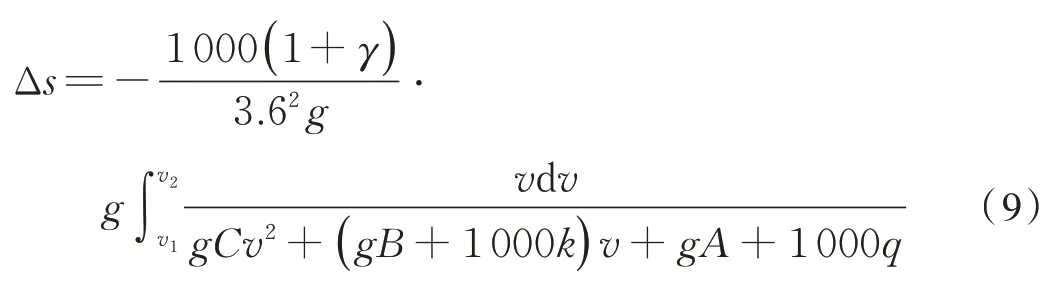
同理,代入式(8)中,可整理出任意速度间隔内对应的有效制动时间积分公式如式(10):
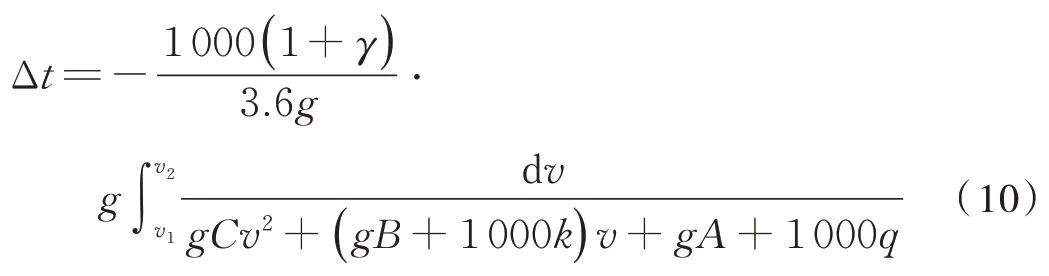
式(9)和式(10)是动车组有效制动过程中距离和所对应时间的模型建立,是文中所研究的重点。此外,需补充的一点是,在整个制动过程中,动车组的总制动距离和所对应的制动时间应为:
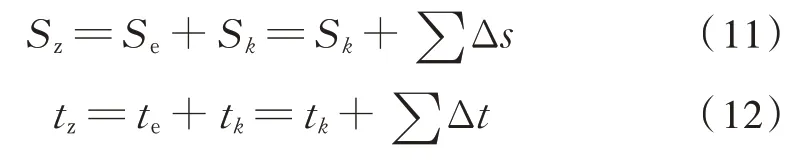
式中:tz、te分别为列车总制动时间和有效制动时间,s;Sz、Se分别为列车总制动距离和有效制动距离,m。
2 基于鱼群算法的制动计算优化
经推导式(9)和式(10)在求取制动计算原函数的过程中有一定的困难性。若采取传统数值积分逼近的方法近似计算[17],会存在求解结果精度低、计算量大且收敛性无法保证等问题。接下来结合不等距分割和人工鱼群算法的原理对以上有效制动计算的积分函数做如下优化。
2.1 相关优化原理
(1)不等距分割原理
考虑到传统数值积分大多都是基于等距节点的求和,只有不断增加更多的节点才能使积分计算得到较高的精度,增大了计算量[18]。利用有效制动距离和制动时间的函数曲线形状,根据曲线的凹凸变化随机选定分割点,这样就减少了节点数,使得计算更为省时且精度高。
(2)人工鱼群算法优化原理
人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)是首次由国内学者李晓磊等人提出的一种模拟人工鱼个体行为的优化策略[19-20],其主要通过构造人工鱼模仿鱼群的觅食、聚群和追尾3种行为来实现全局最优值的目的。利用该算法中随机因素少,具有并行性、快速性和全局性的特点[21],结合不等距分割原理,从而确定任意速度区间内的最优分割点,再利用传统的积分方法求和,得出动车组在整个制动过程中的有效制动积分结果。
2.2 优化实现过程
2.2.1相关定义
由于动车组的有效制动计算是关于速度v的积分表达式,因此在给定速度区间[vi,vi+1]内,设每条人工鱼的状态表示为:V=(v1,v2,…,vn);其中vk(k=0,1,…n)表示为待寻优的控制变量,在文中视为一个不等距分割点;人工鱼在当前位置的食物浓度为目标函数值,表示为y=f(V)(这里的y分别表示Δs或Δt);每条人工鱼之间的距离表示为di,j=‖‖Vi-Vj;人工鱼的感知距离用visual表示;delta表示拥挤度因子,经试验选取delta=0.65;gen表示算法运算的最大迭代次数;try_number表示为最大试探次数;step表示人工鱼移动的步长;n表示参与寻优的人工鱼的数目。
2.2.2适应度函数
在文中每条人工鱼移动一次视为一次优化迭代,鉴于优化Δs和Δt过程中选取的适应度函数结构形式相同,在这里仅列出优化Δs过程中给出的适应度函数方法。该方法如下:
将要考察的人工鱼置于制动速度区间[vi,vi+1]中,计算出该区间内产生n+2个相邻节点之间的距离dj,j=1,2,…n+1;再计算出每个节点所对应的制动距离函数值Δsj,j=1,2,…n+1以及产生n+1个速度小段区间中间点对应的函数值从而确定每小段左端点和右端点的函数值中的最小值minΔsj和最大值maxΔsj,代入适应度函数f(j)=计算,使f(j)逐渐趋向于0,来达到分割方法的最优效果。
2.2.3实现过程
在对动车组制动距离和制动时间进行优化时,根据给定的适应度函数原则按照下述流程对任意速度区间内的有效制动值进行优化计算。(同理仅列出Δs的优化过程)
步骤1设置该算法所需的参数:鱼群数量n,最大迭代次数gen,人工鱼的感知范围visual,最大移动步长step,拥挤度因子delta等;
步骤2初始化鱼群:初始鱼群的选择是在积分区间[vi,vi+1]内随机生成n条人工鱼个体;
步骤3将每条人工鱼按照该适应度函数f(j)=进行计算,公告板中显示最小值;
步骤4对于每条人工鱼执行以下操作
(1)计算出追尾行为、聚群行为的值,(缺省行为是觅食行为)规定鱼的前进方向为最优的行为方向,该鱼向目标方向移动一步。
(2)根据式(9)再不断计算每条鱼的食物浓度函数f(j),其最小值与公告板中的值进行比较,最终使得公告板中始终保持较小值。
步骤5进行判断,若达到文中设定的最大迭代次数,则转步骤6;反之转步骤4。
步骤6程序结束,确定公告板中的值为采取不等距分割法寻优后的最优解。再利用传统的积分方法:代入表达式来求有效制动距离的积分值。
综上所述,动车组有效制动计算的优化过程如图1所示。
3 仿真验证
为了验证人工鱼群算法AFSA方法的有效性,选用动车组车型CRH2和CRH6A为试验验证对象。其中CRH2用于AFSA方法和近似算法的对比,CRH6A用于实例分析。

图1 制动计算流程图
在数据对比之前,先对近似计算法做如下介绍。
3.1 动车组近似计算法介绍
前人在研究动车组制动计算问题时,将列车在每一速度段的运动视为匀变速,利用式(2),提出了一种在任意速度区间内求动车组有效制动距离Δs的近似计算方法。具体方法如式(13):

式中:加速度的单位是m⋅s-2,速度的单位是km⋅h-1,将其单位统一后,上式变为式(14):
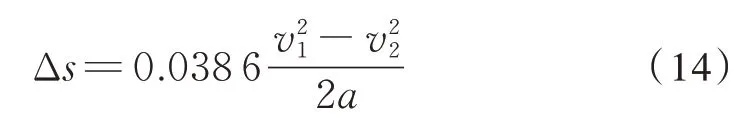
该算法的近似原理是从制动速度区间的初末速度入手,根据初末速度的算术平均值近似计算目标减速度a和单位基本阻力ω0,从而计算出的有效制动距离Se为式(15):

式中:0.008 9是列车回转质量系数γ值取0.001时,单位阻力的减速度系数。
以上近似算法求解的有效制动距离结果存在较大误差,现根据动车组制动过程的速度-时间曲线对产生的误差原因进行分析,见图2所示。

图2 动车组制动过程的速度曲线
从图2中可以看到,动车组在制动过程中所行驶的有效制动距离应为从时刻t1到t2(对应制动速度v1到v2)这段时间内所围成的曲面梯形面积,设该面积为Se1;而式(15)采用近似原理来近似计算制动距离,则其大小为图2中的阴影面积,令该面积为Se2。Se1和Se2存在以下关系:

结合式(15)和图2可以看出,Δe的产生与速度间隔大小v2-v1和k值有关。制动计算时,若选取的速度间隔过大,或选取的目标减速度为v一次函数时,造成计算的结果有偏差是必然的。
3.2 CRH2目标减速度特性参数
查阅设计资料可知,CRH2型动车组制动方式分为EB紧急制动和7级常用制动。制动减速度特性分别由(减速度为常数)、和(减速度为一次函数)3段直线组成。CRH2制动减速度特性参数见表1。

表1 CRH2型动车组的制动特性
3.3 CRH2制动计算其他相关参数
查阅设计资料可知,CRH2型动车组其他相关参数如下:单位基本阻力ω0=0.880+0.007 44v+0.000 114v2,制动空走时间tk=2.3 s,回转质量系数γ=0.10。
将表1中CRH2具体的目标减速度和单位基本阻力中关于速度v表达式中的系数代入式(9)整理,可得在2种不同工况下有效制动距离的具体积分表达式如下:(其中Δs1为常用制动,Δs2为紧急制动)

2种方法计算结果及其差值见表2。
我国《铁路技术管理规程》规定当制动初速度为200 km/h时,紧急制动距离限定在2 000 m以内。从表2可以看出,在常用制动和紧急制动工况下,文中提出的AFSA方法比近似计算法更加有效和精确。原因分析如下:
(1)随着制动初速度的增加,2种方法的结果差值越来越大。原因是采取的近似计算方法弱化了目标减速度在制动计算的重要性,导致计算结果偏小。相比较于近似计算方法,文中视目标减速度为变量,使得制动计算结果更精确。
(2)从表2中我们又可以看到,在区间[0,70]的范围内,AFSA方法和近似计算方法的计算结果又近似相同。原因在于[0,70]的速度区间目标减速度的一次函数系数k=0。
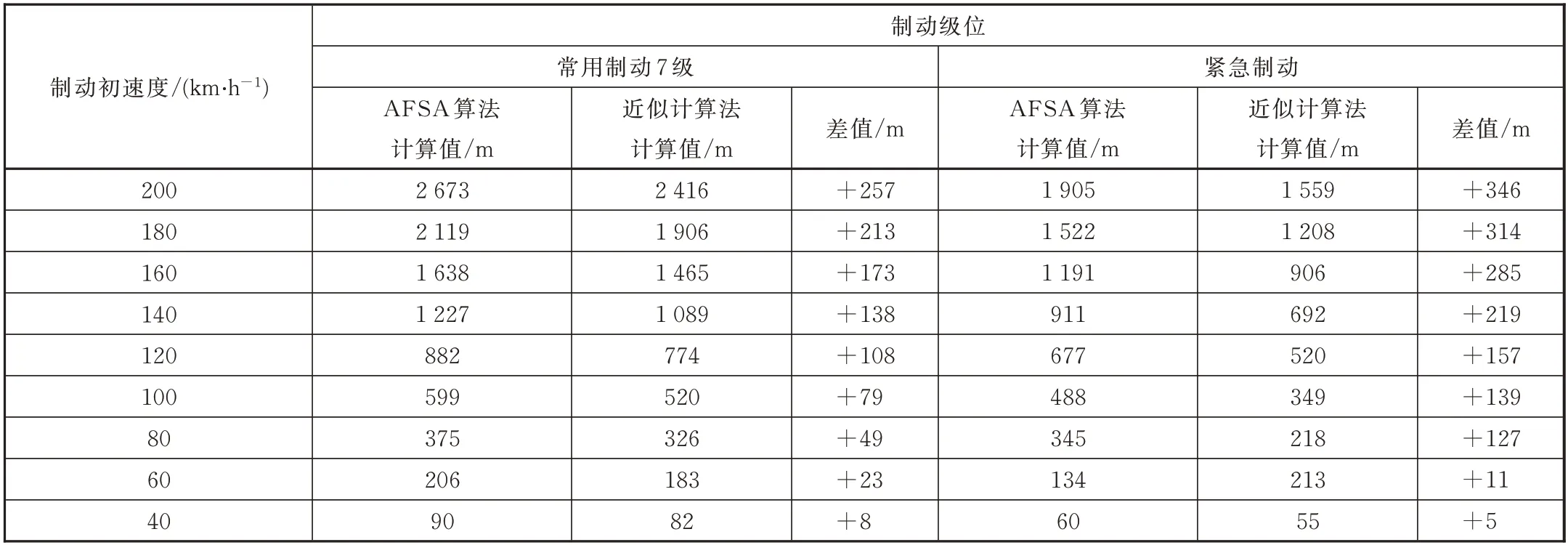
表2 两种方法计算结果及其差值
综上所述,基于不同型号动车组在任意速度区间内的目标减速度特性的差异,近似计算方法存在弊端且有一定的局限性,而AFSA方法能很好的避免这一问题。
4 实例分析
为了进一步验证AFSA方法的有效性,以及近似计算法在制动计算中带来的较大误差,我们选取CRH6A型动车组的常用制动工况3~7级为测试对象。
4.1 CRH6A目标减速度特性参数
查阅设计资料可知,CRH6A型动车组制动方式分为EB紧急制动和7级常用制动。制动减速度特性分别由(减速度为常数),以及(减速度为一次函数)5段直线组成。CRH6A制动减速度特性参数见表3。
4.2 CRH6A制动计算其他相关参数
查阅设计资料可知,CRH6A型动车组其他相关参数如下:单位基本阻力ω0=0.551+0.001v+0.000 166v2,制动空走时间tk=1.5 s,回转质量系数γ=0.05。
将表3中CRH6A具体的目标减速度和单位基本阻力中关于速度v表达式中的系数代入式(9)和式(10)对其进行运算,整理可得动车组在常用制动7级下的有效制动距离和对应有效制动时间的具体积分表达式如式(18)和式(19)所示(制动级位3~6级的积分表达式计算过程和7级一样,文中就不一一赘述)
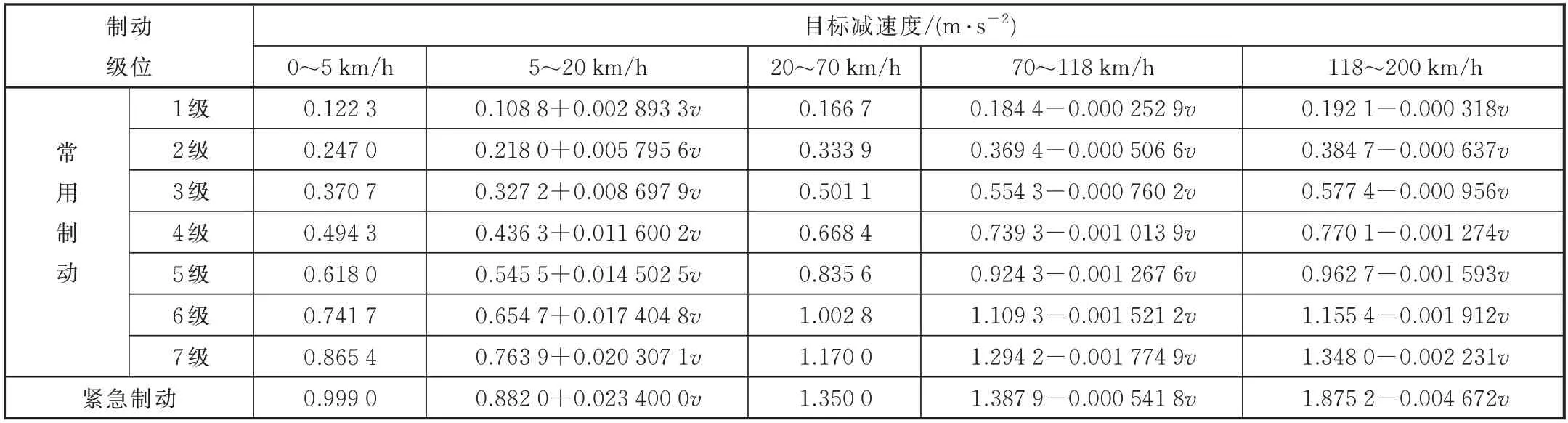
表3 CRH6A型动车组的制动特性

使用文中提出的AFSA计算方法和近似计算法对CRH6A型动车组在平直道上的制动距离进行计算,2种方法的计算值与CRH6A的实测值见表4。其中,误差1为近似计算法与AFSA算法的差值;误差2为近似算法与CRH6A实测值的差值。
表4中误差1显示,在速度区间[80,200]内,近似计算法与AFSA算法的结果差在制动初期较大,随着制动速度的降低,差值会变得较小。这符合表2中分析2种方法在速度区间[40,200]造成差值变化由大到小的原因;误差2显示,近似计算法与实测值的差值很大,可见近似算法造成的较大误差并不适用动车组制动系统的设计;表中误差显示,在常用制动停车工况下,AFSA方法求得CRH6A的制动距离与实测结果相当接近。其中最大的制动距离误差为6.71%,最小误差不足1%,平均误差在5%以下。由此表明AFSA算法比近似计算法更适用求解动车组的制动计算。
文中还给出了AFSA算法在平直道环境下求解CRH6A型动车组制动时间的计算值,见表5。
由表5可见,在常用制动停车工况下,AFSA方法求得CRH6A的制动时间与实测结果也相当接近。其中最大的制动时间误差为8.54%,最小误差为0.48%。
表4和表5表明,AFSA算法所得计算结果具有较高精度且与CRH6A的实测结果具有良好的一致性,可在理论计算层面满足制动距离和制动时间的要求。
此外,从表4和表5也可以看出,随着制动初速度的减小,AFSA算法下的制动距离和制动时间的误差越来越大。主要原因是当前我国动车组制动控制模式主要采用速度黏着控制,其制动控制装置利用目标减速度计算所需的制动力并采用设定的平均摩擦系数,计算得到所对应的制动缸压力来实施控制。随着制动初速度的减小,摩擦副的实际平均摩擦系数越来越大,导致实际制动力大于所需制动力,实际的制动距离和制动时间小于理论的计算结果。
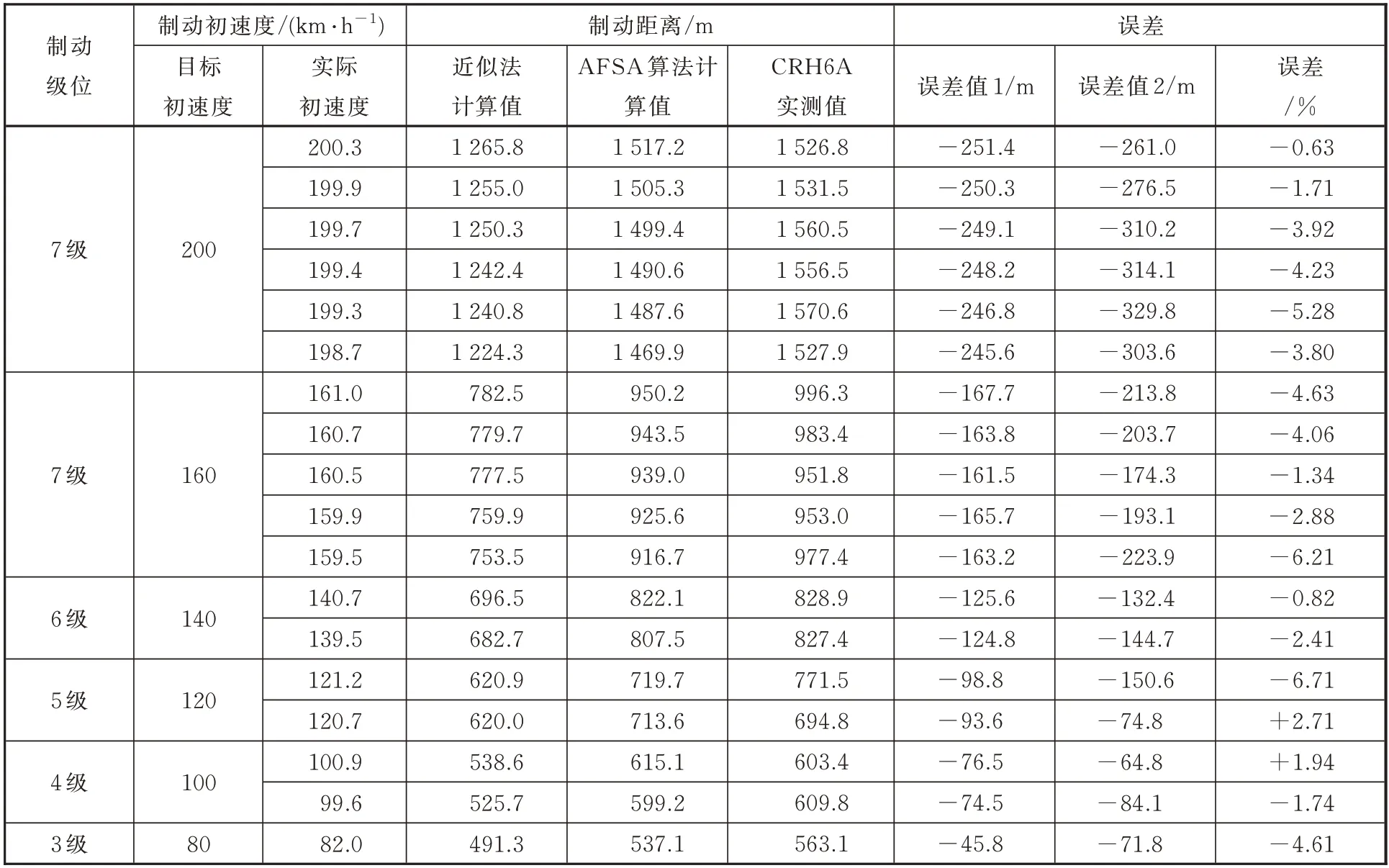
表4 两种方法下的CRH6A型动车组常用制动距离的计算值与试验值的比较
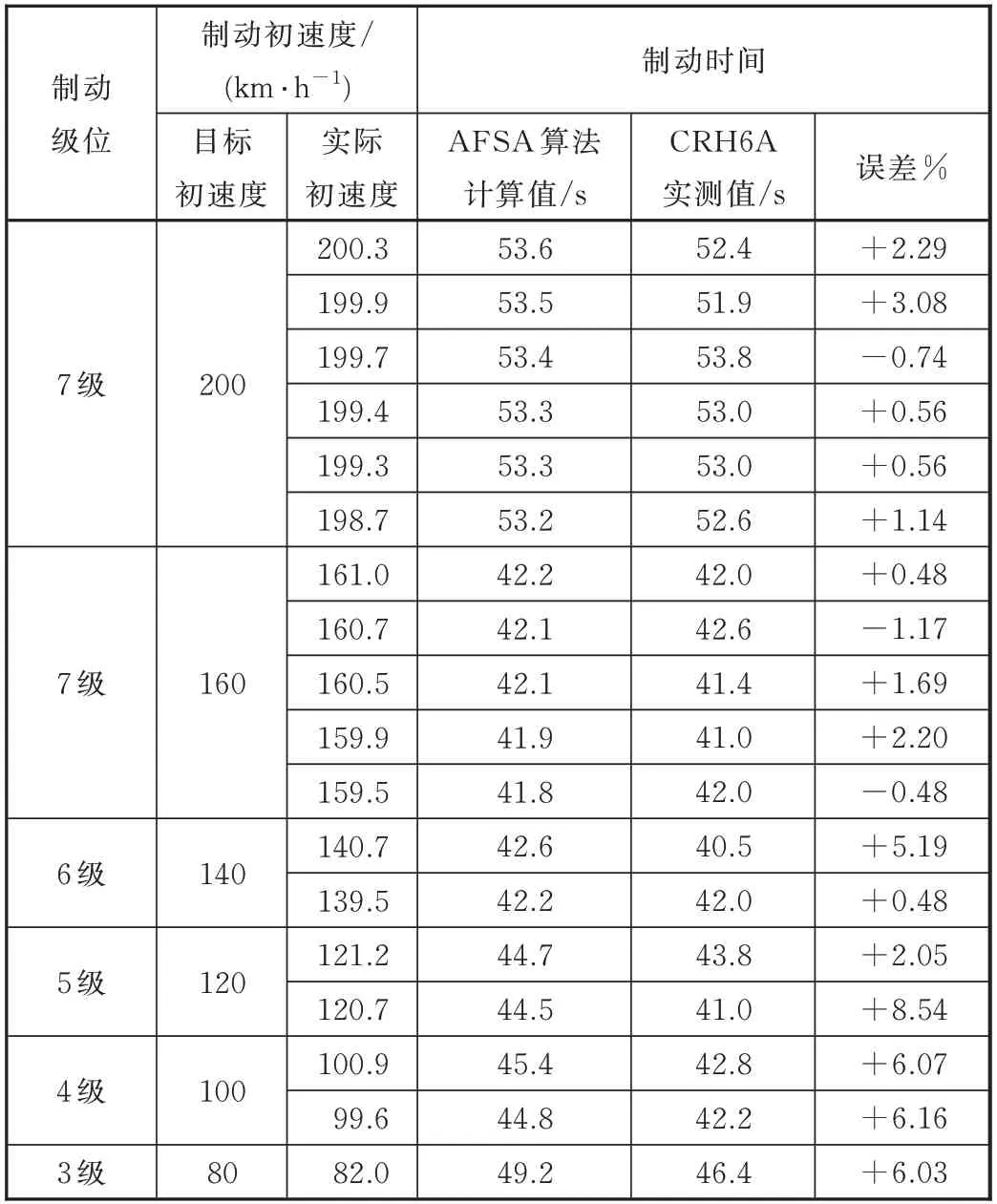
表5 AFSA算法下的CRH6A型动车组常用制动时间的计算值与试验值比较
5 结论
(1)动车组与常规列车在速度、牵引和制动性能上有很大差异,套用既有公式进行制动计算已不适用动车组,其计算结果会与实测结果产生较大误差。
(2)文中提出的人工鱼群算法AFSA优化制动计算,可以得出在误差允许范围内的有效制动距离值,通过对CRH6A的实测数据对比,结果表明该算法十分有效,积分精度高。该方法的提出可为动车组制动计算提供新思路,同时为后续动车组站内停车系统的设计提供参考。
