带支撑粘弹性阻尼器耗能框架结构随机振动分析
2021-03-19陈钰雪邵海浪
张 敏, 付 熊, 陈钰雪, 邵海浪
(1.江西科技师范大学 建筑工程学院,南昌 330013; 2.广西科技大学,土木建筑工程学院,柳州 545006)
1 引 言
粘弹性阻尼器是一种被动耗能减震装置,由于其安装方便、性能稳定、耗能能力强等优点,在土木工程领域广泛使用。文献[1,2]表明,粘弹性阻尼器具有良好的耗能能力。但粘弹性阻尼器需要支撑才能安装在结构上,支撑刚度对结构地震响应影响较大[3-5]。文献[6]对人字形支撑粘弹性阻尼器进行地震时程分析,发现合理设置支撑的粘弹性阻尼器耗能能力较强。文献[7]对设置带支撑粘弹性阻尼器的钢筋混凝土结构进行抗震性能研究,结果表明合理设置支撑的粘弹性阻尼器加固技术较传统抗震加固技术好。文献[8,9]推导了带支撑粘弹性阻尼器的支撑刚度公式,并给出了支撑刚度取值范围。文献[10]对设置不同耗能阻尼器的五层钢框架模型进行地震响应分析,试验表明合理设置的耗能阻尼器支撑能够显著降低结构地震响应。文献[11]对设置粘弹性消能支撑网格屋盖的实际工程进行地震响应分析,试验表明合理设置的粘弹性消能支撑可以显著降低屋盖结构的响应。文献[12]提出了考虑支撑等连接刚度的减震体系模型并对单自由度体系进行了验证,结果表明支撑刚度系数取值对消能减震结构具有重要意义。文献[13]分析了带支撑粘弹性阻尼器在不同支撑系数和松弛时间系数下对结构的地震响应,并给出了两者取值范围。以上分析主要采用时程分析法对带支撑粘弹性阻尼器进行地震响应分析,但由于地震具有随机性,文献[14-18]给出了地震动的随机模型,在此基础上,一些学者采用随机振动理论对带支撑粘弹性阻尼器结构进行了随机分析。文献[19]对带支撑的粘弹性阻尼器多层隔震结构进行随机响应分析,结果表明支撑刚度越大,结构随机响应越小。文献[20,21]对设置带支撑粘弹性阻尼器结构进行非平稳随机分析,结果表明支撑刚度越大,随机响应越小。文献[22]对带支撑粘弹性阻尼器的高层结构进行随机风振响应分析,结果表明支撑刚度越大,风振位移响应越小。
国内外还有不少学者对带支撑粘弹性阻尼器地震响应进行了大量研究。本文采用随机振动理论对带支撑粘弹性阻尼器框架结构的地震响应进行随机分析。首先研究阻尼器的支撑刚度和松弛时间系数等对粘弹性阻尼器复合刚度的影响规律,在此基础上根据随机振动理论,分析带支撑粘弹性阻尼器框架结构的层间位移角和地震作用等地震反应均方差,从而研究粘弹性阻尼器支撑刚度对框架结构地震反应的影响规律,并将分析结论与文献[13]采用时域分析法所得结论进行对比,由此为设置带支撑粘弹性阻尼器框架结构的工程设计提供依据。
2 粘弹性阻尼器模型
本文粘弹性阻尼器模型采用Maxwell模型,该模型由刚度元件和阻尼元件串联而成,如图1所示。带支撑粘弹性阻尼器模型如图2所示,该模型考虑了阻尼器支撑的刚度参数。
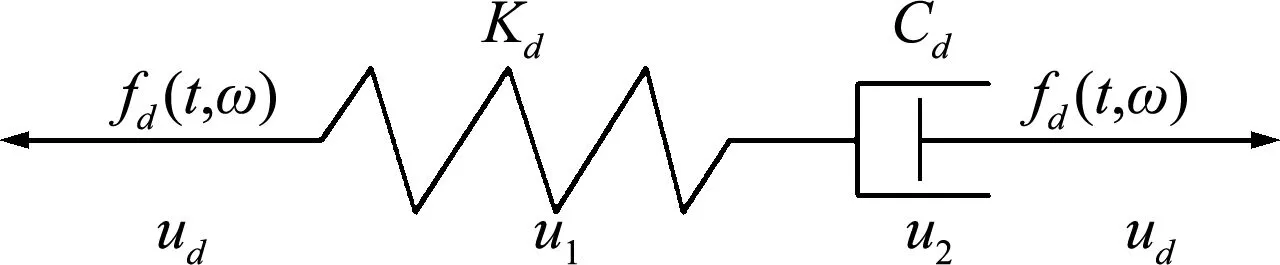
图1 粘弹性阻尼器模型

图2 带支撑粘弹性阻尼器模型
图1模型中粘弹性阻尼器阻尼力为
(1)
ud(t)=u1(t)+u2(t)
(2)
式中fd(t,ω)为粘弹性阻尼器阻尼力,Kd和Cd分别为粘弹性阻尼器的刚度系数和阻尼系数,u1(t)和u2(t)分别为图1刚度元件和阻尼元件对应的变形,ud(t)为图1阻尼器的总变形。
对式(1,2)进行傅里叶变换可得
Fd(ω)=KdU1(ω)=iωCdU2(ω)
(3)
Ud(ω)=U1(ω)+U2(ω)
(4)
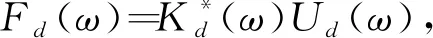
(5)

(6)
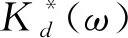
图2模型中带支撑粘弹性阻尼器的作用力为
(7)
u(t)=us(t)+ud(t)
(8)
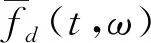
对式(7,8)进行傅里叶变换可得
(9)
U(ω)=Us(ω)+Ud(ω)
(10)

(11)
式中K*(ω)为带支撑粘弹性阻尼器的复刚度。
对式(11)化简可得
(12)
由式(5)可得
(13)
(14)
3 随机振动方程求解
在结构各楼层均安装一个带支撑粘弹性阻尼器,如图3所示。结构的质量矩阵为[M]∈Rn,结构的自身阻尼矩阵为[C]∈Rn,结构自身的刚度矩阵为[K]∈Rn。在随机地震激励作用下,结构振动方程为

(15)

对式(15)进行傅里叶变换,可得
(iω)2[M]{X(ω)}+(iω)[C]{X(ω)}+[K]{X(ω)}+
(16)


(17)

图3 框架结构计算简图
将式(16)化简为
(18)
{H(ω)}=-{-ω2[M]+(iω)[C]+
[K]+[K*(ω)]}-1[M]{1}
(19)
根据随机振动理论,解得第j楼层xj(t)自相关函数为
(20)

xj(t)的自谱密度为
(21)
xj(t)的方差为
(22)
xj(t)的均方差为
(23)
结构层间位移向量{Δ}可以表示为
{x(t)}-[B]{x(t)}
(24)
式(24)可以化简为
{Δ}=([I]-[B]){x(t)}
(25)


解得第j楼层Δj自相关函数为
[([I]-[B]){H(ω)}]ei ω τdω
(26)
Δj自谱密度为
[([I]-[B]){H(ω)}]
(27)
响应Δj方差为
(28)
响应Δj均方差为
(29)
层间位移角均方差向量为
δθj=δΔj/h
(30)
式中h为结构楼层高度。
4 随机地震动模型
假设地震是平稳随机过程,描述地震动随机过程的模型有很多种[14-18]。本文选取改进Kanai-Tajimi模型(胡聿贤谱)进行结构随机分析。
(31)
式中S0为谱强度,ωg,ξg和ωc分别为场地特征频率、场地特征阻尼比和低频截止频率。由文献[23]可得改进Kanai-Tajimi功率谱参数,列入表1。
5 地震作用分析
一般采用反应谱理论[24]分析结构所受地震作用。本文根据随机振动理论,推导设置带支撑粘弹性阻尼器框架结构地震作用计算公式如下。
令{x(t)}=[Φ]{q(t)},则
{q(t)}=[Φ]-1{x(t)}
(32)
式中 [Φ]=[{Φ1},{Φ2},…,{Φj},…,{Φn}]为无阻尼器结构振型矩阵,{Φj}为结构第j阶振型向量,{q(t)}为广义坐标向量。

表1 改进Kanai-Tajimi模型参数
式(32)进行傅里叶变换可得
{Q(ω)}=[Φ]-1{X(ω)}
(33)
将式(18)代入式(33)可得
(34)
解得响应qj(t)的自相关函数为
([Φ]-1{H(ω)})ei ω τdω
(35)
响应qj(t)的方差为

(36)
响应qj(t)的均方差为
(37)
设置带支撑粘弹性阻尼器结构各楼层地震作用向量为
{F(t)}=[K]{x(t)}
(38)
将{x(t)}=[Φ]{q(t)}代入式(38),化简可得
(39)

结构第j阶振型对应的地震作用向量为
(40)
式(40)进行傅里叶变换,可得
(41)
则{Fj(t)}均方差向量为
(42)

6 工程算例
算例工程[25,26]为一栋10层混凝土框架结构楼,底层层高为4.5 m,其余各层层高均为3.3 m,结构总高度为34.2 m;该结构设防类别为丙类,抗震设防烈度为8度,基本地震加速度为0.3 g,设计地震分组为第二组;结构自身阻尼比ξ=0.05;混凝土强度等级为C30;楼屋面折算恒载标准值为 10 kN/m2(包括墙体自重),楼屋面活载标准值为2 kN/m2;梁截面尺寸为300 mm×650 mm,柱截面尺寸为600 mm×750 mm。框架结构局部平面如图4所示;框架结构各层均布置带支撑粘弹性阻尼器,阻尼器的阻尼系数均为5×107N·s/m,计算简图如图3所示。

图4 框架结构局部平面图(单位:mm)
6.1 支撑参数对结构响应的影响
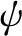
6.2 结构响应分析

图5 框架结构最大层间位移角均方差
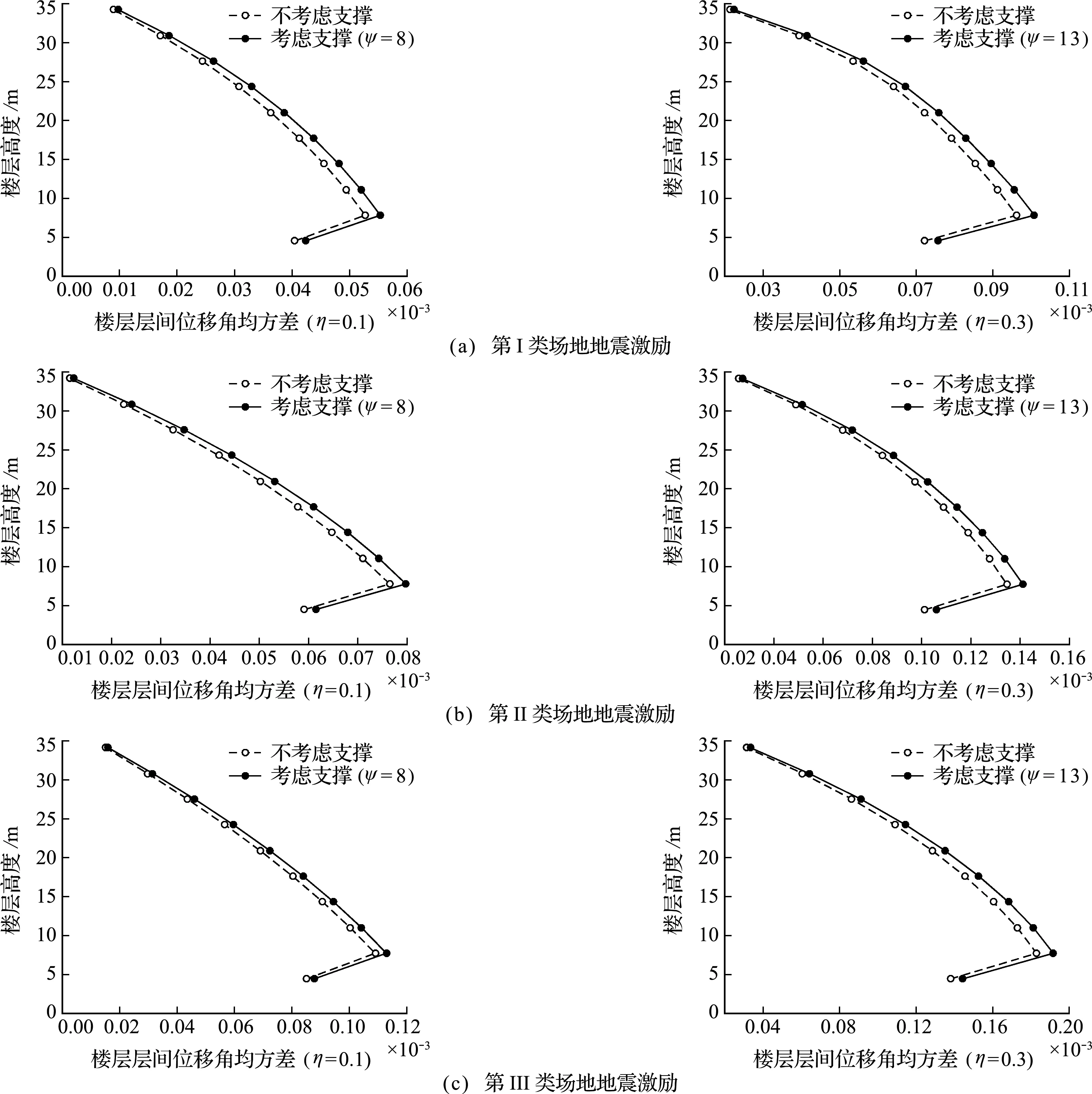
图6 框架结构层间位移角均方差
6.3 阻尼器松弛时间系数对结构响应的影响
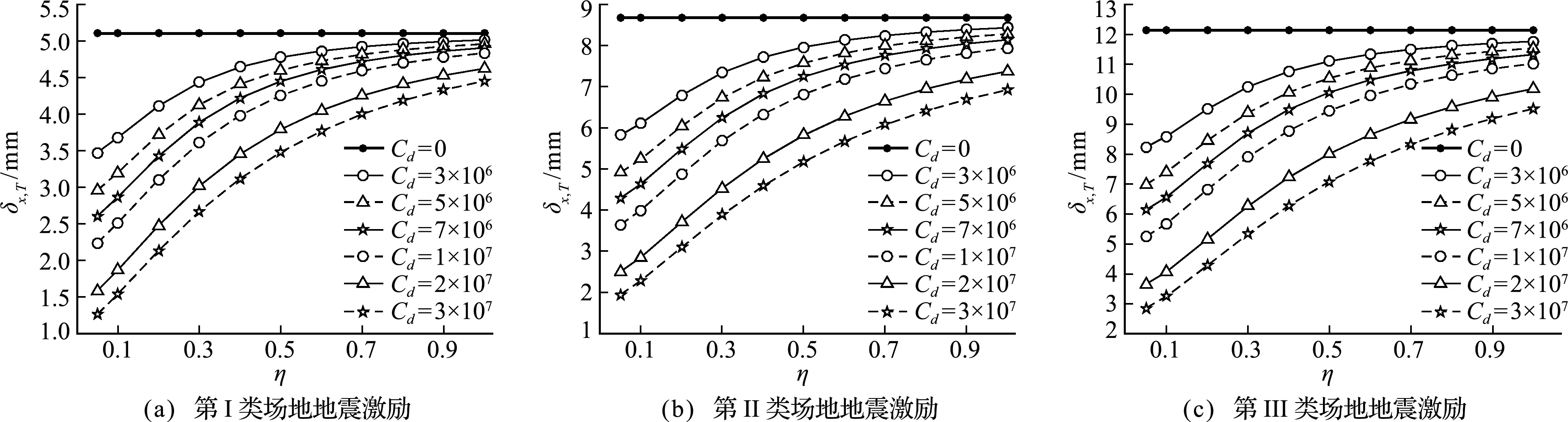
图7 框架结构顶层位移均方差

图8 框架结构地震作用均方差
6.4 地震作用分析
7 结 论
上述分析与文献[13]的结论基本一致。本文对设置带支撑粘弹性阻尼器框架结构地震反应的随机分析,结论如下。


