河道二维数值模拟地形数据前处理精细化研究
2021-03-19赵科锋曹慧群罗平安
赵科锋,曹慧群,罗平安
(长江科学院 流域水环境研究所,武汉 430010)
1 研究背景
随着经济及城镇化发展,地表水环境问题越来越突出,尤其是城镇河流、湖泊等地表水体受到越来越严重的污染。为了研究地表水水环境变化状况,许多学者通过建立数值模型,分析地表水水动力水质变化规律。国内外针对地表水水动力、水质、泥沙的数值模拟软件主要有EFDC、MIKE、Delft3D、CJK3D等[1],而地表水数值模拟的一个重要内容是地形模拟,地形模拟的好坏直接影响模拟结果的准确性与可信度[2]。针对地形模拟,部分学者开展了相关研究,如:任勇等[3]对金沙江河道不规则三角网进行人工干预和优化,达到快速、合理、准确生成等高线的目的。侯明瑞[4]将元胞方法引入地形重构过程中,通过将复杂的河流动力学过程进行简化,建立基于元胞方法的地形重构模型,此种模型能较好避免地形构造生成的非自然条带状地形。陈中[2]利用SMS软件,提出了一种基于三角网格的内插技术。而在众多的研究当中,针对地形数据优化的方法却较少。地形模拟的优劣极大影响模型的准确性,而受人力、物力、财力及技术等条件的限制,无法对河流、湖泊等地表水体进行全覆盖测量,实际操作中,仅能进行有限的断面测量,导致地形模拟严重不符合实际情况,影响模型准确性,甚至造成模型不收敛,导致无法计算。
MIKE是由丹麦的DHI公司开发的一款非常优秀的应用于水动力、水质、泥沙输移等方面的软件,MIKE可用于河流、湖泊、水库、河口、海湾等的一维、二维、三维模拟[5],水底地形插值是MIKE建模必不可少的重要环节[6]。目前,研究者使用较多的断面地形细化方法,是通过第三方模拟软件进行插值后,导出插值数据,而这种方法操作复杂,依然无法解决任意断面数及任意距离的插值计算,且常常导致地形数据出现较大的偏差[7-8]。为了解决因实测断面地形数据不足导致的模型插值与实际情况偏差较大的问题,本文通过对研究区河道边界节点编码,利用实测断面坐标对编码进行识别,可沿河道弯曲方向插值,实现纵向任意断面数、横向任意距离的河道地形插值优化,避免因地形数据量少而生成异常地形的问题,达到减少模型运算错误率及模型更接近真实情况的目的。
2 地形数据前处理精细化方法
2.1 边界及断面数据编码
MIKE21模型边界基础数据是由连续坐标点组成的,描述连续坐标点的方法应用较多的是样条曲线法[9],然而对于弯曲较大的河道,样条曲线无法准确描述河道边界形状。为此,本文提出对河道边界节点进行编码(编码与坐标一一对应),通过遍历所有边界节点,识别出距实测断面最近的边界节点,根据定位的边界节点及设置的插值断面距离(如图1中x),计算内插断面的编码(如图1中A1、A2等),由此可识别出所有插值断面的边界节点编码,进而确定新增断面坐标。节点编码及识别方法为:利用ArcGIS对河道左、右岸边界进行等间距取节点(间距设置成1 m为宜),并对每个节点进行编码,通过节点遍历,识别出距实测断面最近的节点。需要注意,边界文件(MIKE21能识别扩展名为xyz的格式)分左、右岸2个节点坐标文件,断面上实测点需按上游至下游、左岸至右岸的规则编写文件。河道左、右岸分别为ABC、abc,实测断面为Aa、Bb、Cc,新增内插横向断面为A1a1、A2a2等,新增内插纵向断面为Ⅰ、Ⅱ、Ⅲ,如图1所示。
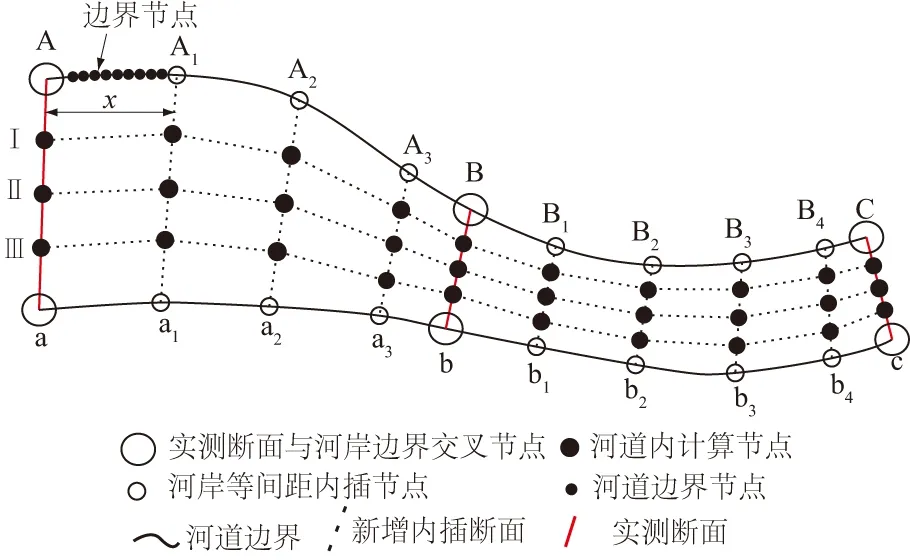
图1 河道边界编码计算示意图Fig.1 Schematic diagram of coding of river boundary
2.2 内插节点坐标及高程计算
内插节点坐标计算包括横向断面及纵向断面节点坐标计算。横断面节点坐标计算:根据河道左、右岸边界上确定的断面节点及设置的插值断面间距,计算内插断面的编码,由编码确定相应的坐标。纵断面节点坐标计算:根据每条横断面两端节点,确定等间距纵向断面节点,扩展方式如图2所示。
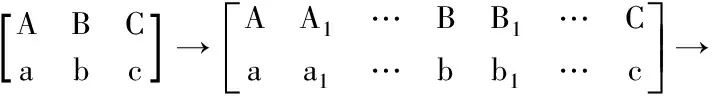
图2 节点坐标内插示意图Fig.2 Schematic diagram of node coordinate interpolation
主要步骤有:①从地图上矢量化河道边界(河道左岸及右岸),得到KML或SHP等格式的文件;②利用ArcGIS对河道左、右岸分别进行等间距取点,得到左、右岸多组边界节点坐标文件;③断面上实测点按上游至下游、左岸至右岸的规则编写文件;④利用实测河道横断面距河道最近一个节点坐标,遍历对比河道边界所有节点坐标,获取实测断面与河岸边界最近节点(此节点与交叉点相距极小,近似为交叉点,如图1中点A、B、C)的编码;⑤根据设置的横向断面剖分间距x(如图1中所示),计算两实测断面间河道边界等间距内插节点编码,如图1中点A1、B1等;⑥根据纵向剖分断面数量,计算实测断面(图1中Aa、Bb等)及内插断面(A1a1、B1b1等)相应的河道内等间距节点编码;⑦根据2条实测断面河底高程,插值计算两实测断面间河道内节点河底高程值及相应编码;⑧对各剖分节点坐标与河底高程进行编码匹配,最终得到多组河底精细化坐标点及对应的河底高程。
2.3 插值计算关键代码模块
由于计算量较大,手动计算费时费力,且出错率高,通过编写程序,可便捷实现河道地形精细化内插,获取大量地形数据,达到快速、准确建立数值模型的目的。关键代码模块主要包括:①河道左、右岸边界距断面最近点求解模块;②实测横向断面间内插断面编码计算模块;③纵向断面内插节点编码计算模块;④内插节点河底高程插值模块;⑤内插节点坐标与高程匹配模块;⑥数据显示、输出模块。
3 实例应用
为了检验河道地形内插生成精细化地形数据的准确性与适用性,本文选取荆门城区某河流部分河段作为研究对象,根据河道实测断面地形数据,沿河道弯曲方向进行精细化插值计算,并选取部分断面实测数据进行对比验证。
3.1 河道基本情况
研究河道长约1.0 km,宽约18~60 m,河道弯曲变化较大。为研究河岸污水处理厂排污对下游监测断面水质的影响,拟建立二维水动力水质模型进行预测,为此,开展了河道地形测量,现场共测量断面10组,每个断面等间距测量7组高程点,共计70个测量点,断面位置如图3所示。
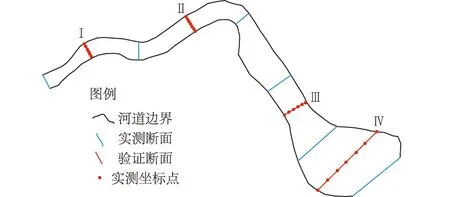
图3 河道地形测量断面位置Fig.3 Location of sections for river topographic survey
3.2 河道地形精细化插值及检验
利用6个实测断面地形数据进行地形精细化内插计算,4个实测断面地形数据作为检验。横向断面间距设置为20 m,纵向断面数设置为7,利用Python编写的程序自动生成约60组断面,共约420个坐标点,如图4所示。
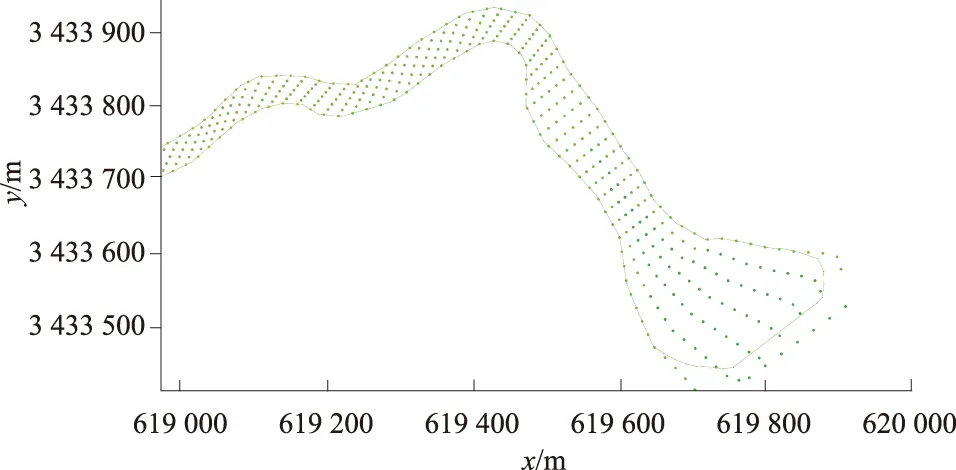
图4 经程序插值后生成内插节点Fig.4 Nodes generated by programming afterinterpolation
根据生成的内插节点坐标,利用MIKE邻近点法插值,生成研究区河道地形,如图5(a)所示。未经断面内插计算,直接通过10组实测地形数据生成的河道地形如图5(b)所示。从图5(a)、图5(b)的对比可以明显看出,经河道断面精细化内插计算生成的河道地形较为合理,河道地形较为平滑;而未经河道断面精细化插值计算,直接利用实测断面生成的河道地形明显不准确,甚至出现河道中泓地形高于河道两岸地形的情况,这主要是由于河道较长,河道宽度较小,而实测断面相距较远,数据量较小,导致MIKE软件插值不合理。
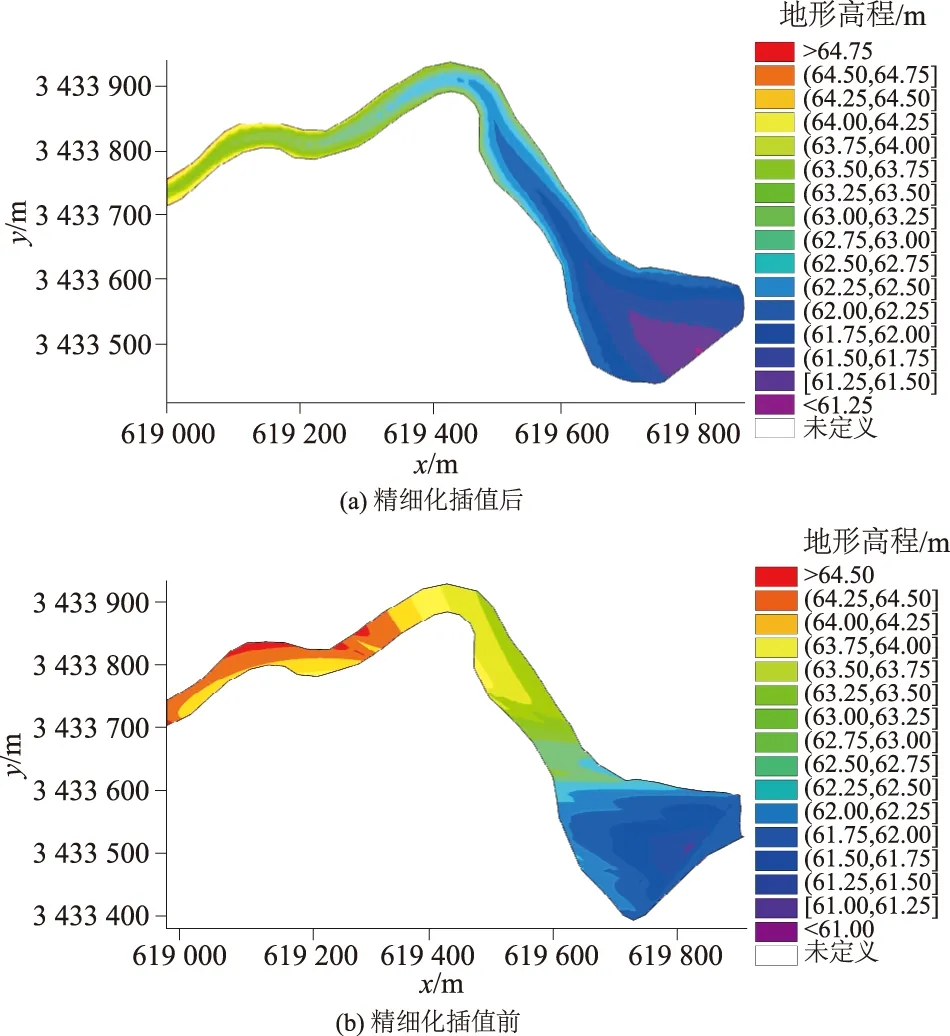
图5 河道地形精细化插值和未精细化插值计算地形Fig.5 Topography maps before and after refined riverchannel interpolation
本文利用4组实测断面数据进一步检验精细化插值计算后生成的河道地形的准确性。通过对比河道断面对应高程实测值与精细化计算值及未精细化计算值(通过第三方软件插值计算),分析河道地形精细化内插后的准确性,如图6所示。28组地形高程实测值与精细化计算值中,相差最大为0.148 5 m,最小为0.012 1 m,平均为0.076 6 m,相对误差均不到1%;而实测值与未精细化计算值中,相差最大为1.510 5 m,最小为0.011 0 m,平均为0.511 4 m。从分析结果来看,经程序精细化内插计算后的河道地形能较好地反映原始河道地形,为研究区建立二维水动力水质模型提供了大量可靠的基础数据,同时,减少了因数据量少导致的模拟地形不合理的情况,提高了数值建模的效率及准确性。
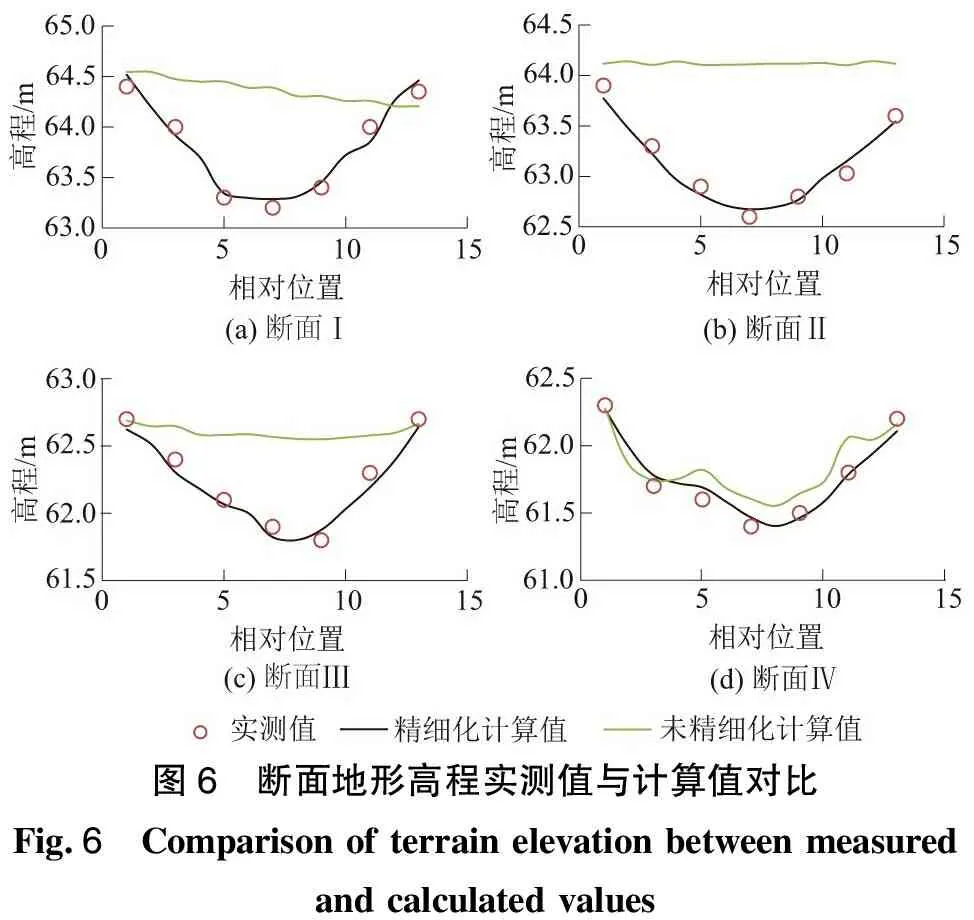
图6 断面地形高程实测值与计算值对比Fig.6 Comparison of terrain elevation between measuredand calculated values
4 结 论
(1)地形模拟的优劣极大影响了模型的准确性,而受人力、物力、财力及技术等条件的限制,无法对河流、湖泊等地表水体进行全覆盖地形测量,实际多数操作中,仅能进行有限的断面测量,导致地形模拟严重不符合实际情况,甚至导致模型不收敛。
(2)样条曲线法无法准确描述弯曲较大的河道,而通过对河道连续点编码定位坐标点,结合设置的插值横向断面间距及插值纵向断面数,可以沿河道方向计算内插节点坐标及高程,此方法能较好地精细化河道地形。
(3)选取荆门城区某河流部分河段进行检验,利用编写的程序结合实测断面精细化河道地形,对比地形实测值与计算值,可以看出,计算河道断面与实测断面基本一致,测量点高程相差最大为0.148 5 m,平均为0.076 6 m,精细化内插生成的地形基本能反映原始河道地形。
(4)通过编写程序,能实现任意横向断面间距及任意纵向断面数的精细化坐标计算,此方法生成的河道地形数据,能应用于MIKE、EFDC、SMS、Delf3D等地表水数值模拟软件,并减少模型出错率,提高模型精度。
