基于改进的神经网络最近邻聚类算法 在结晶器液位系统中的应用
2021-03-19缸明义陈立辛宁平华夏兴国
缸明义,陈立辛,宁平华,夏兴国
(1.马鞍山职业技术学院 电气工程系,安徽 马鞍山 243031;2.安徽科技学院 机械工程学院,安徽 凤阳 233100)
对于连铸过程的控制而言,关于结晶器液位的精确检测及有效控制非常重要。通常,可通过常规PID控制算法来进行控制。但是在突发的干扰情况下,常规的PID 控制往往很难适应,甚至无法稳定控制系统。比如由渐进性的金属氧化物在浸入式水口中堆积而造成的堵塞,会因为突然放出氧化物而产生“开堵”现象,流动特征和塞棒位置因此而变化,从而使开堵时液位骤然升高,如果控制效果好,常规PID 可以使液位从不稳定状态逐渐恢复到稳定状态。但在某些情况下,则可能会发生钢水溢流,造成连铸机停机[1-3]。
针对常规PID 的不足之处,提出基于神经网络的智能PID 和模型辨识相结合的控制方法,它不受被控对象数学模型的限制,能够在线实时辨识出系统的模型并在线修改神经网络的权值,优化系统的控制性能。
1 结晶器液位系统模型

图1 结晶器液位模型方框图
结晶器主要是通过水来进行冷却,通常为钢锭模。当有钢水经由该部件之后,将会得以迅速且均匀的降温冷却,由此就有一个初生坯壳得以形成,它通常有较好的表面质量以及均匀的厚度,确保整个连铸过程得以完成。在设计结晶器时,最为关键的就是要使铸坯上有良好的坯壳形成,由此,当受到热应力以及机械应力等的共同作用时,也不会导致铸坯的断裂或是变形。图1详细地展示了它的结构形式。
该系统共包括4 个不同的组成部分成,即:塞棒流量控制特性与电动缸伺服系统(执行机构),结晶器特性模型(被控对象)以及液位检测传感器(检测环节)[4]。其输入信号为实际值和液位给定值二者之间的偏差信号,经由逻辑运算将电信号输出,接着利用执行机构来对其进行转换,从而成为相应的位置信号,再通过调节塞棒开启度来对钢水的流入量进行有效控制,由控制器来持续地调整偏差信号,从而保持液位位于给定值之上。根据结晶器的积分特性可以获得结晶器中的钢水液位。图 1 中,r,e,u,tx ,inQ ,outQ ,h 分别为液位设定值、液位偏差、控制器输出电信号、塞棒位置、钢水流入量、钢水流出量、结晶器液位高度。
1.1 伺服驱动模型
交流伺服系统的理想化数学模型是典型的二阶动态系统,根据矢量控制、电流耦合的方法可以得到电机的数学模型,而且模型和电流环时间常数、电机时间常数等有关系。结合文献[5],将其简化为一阶惯性环节:

其中, k1=1, T1取0.23 s。
1.2 塞棒流量特性模型
塞棒流量特性是指塞棒位置与结晶器钢液流入量之间的关系,即:

式中,inQ 为结晶器钢水流入量。
塞棒的工作流量特性可用如下模型表示:

此处,maxtX 代表了最大的塞棒开度,maxQ 代表了全开塞棒的情况下,最大的钢液流量,vP 代表了全开塞棒的情况下其节流口区域上压降和总压降二者之间的比值, )(⋅f 则代表了节流口上所对应的理想流量特性,一般可通过产品手册来进行查询。而vP 值可通过实验来测得。
一般来说,难以利用公式来准确地进行节流元件相关流量特性的表达,它仅可被用来对固有的流量特性进行选择,或者是开展近似补偿方面的处理,在进行手册查询后,则需辨识修正流量特性。
在钢液经由中间包而逐渐地流进结晶器的过程中,主要利用浸入式水口来进行钢液的传输,则钢水流入量和塞棒位置间所具有的动态特性体现为延迟的特性,可通过下式来描述:

式中,τ 为时间常数, 8.0~4.0≈τ ,本文取0.5。QK 为塞棒节流口的流量增益。
1.3 结晶器模型
对于该控制系统而言,拉坯速度对结晶器中的具体钢坯量起到控制的作用,而塞棒的位置则会影响其钢水的流入量,所以可将结晶器特性视作积分器,则有:

式中,mA 为结晶器截面积。
考虑到结晶器有很小的延时,故用一阶惯性环节表示:

其中,2K 为结晶器截面积mA 的倒数,ξ 取0.1 s。
结合各个部分传递函数得出结晶器液位系统的传递函数为

2 基于RBF 神经网络的结晶器液位控制系统模型
2.1 RBF 神经网络的结构
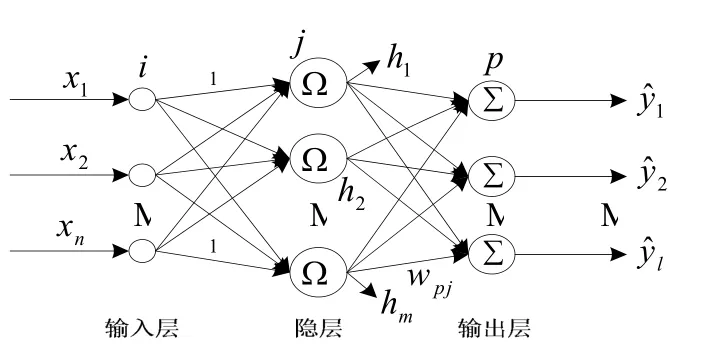
图2 RBF 网络结构
RBF(Radial Basis Function)是一类具有单隐层的三层前馈网络,在模式识别等领域都有着广泛的应用(图2)。从结构来看,其第2层(也就是隐含层)为通过一系列的径向基函数共同地构成的非线性映射层。输入层-隐含层之间的变换为一种非线性的变换,而隐含层-输出层之间所对应的变换则为一种线性变换。图2详细地描述了该类神经网络所具有的结构形式。
输入层单元(其数量为n 个)和输入模式中的特征参数(其数量也为n 个)相对应,而输出层单元(其数量为l 个)则和系统输出相互对应,以高斯基函数来作为隐含层所需的激活函数,由该函数来响应输入信号。
隐含层的Gussain 函数表示为
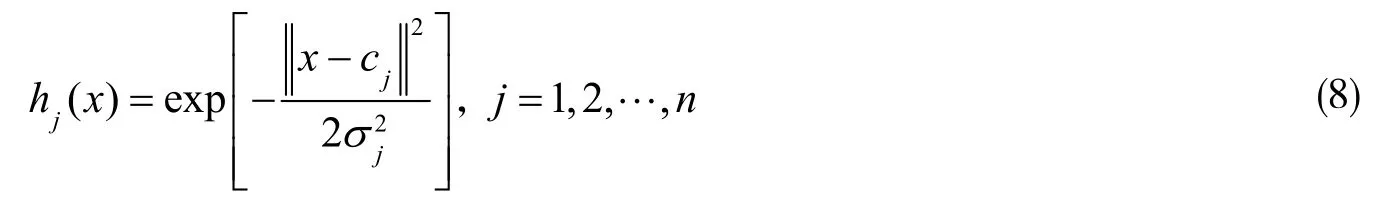
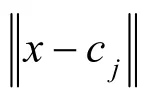

式中, x =( x1, xx, …, xn)T为输入向量, wpj为连接权值。对任意x,作为Gussain 函数均有 hj( x)>0,它无法在局部调整权值。 hj(x)在x 远离c 时无限小,可近似为零。因此,当 hj( x)>某一数值(例0.06)时,对其权值 wpj才做修改。由此,RBF 网络也拥有了局部逼近网络且学习速度快的优点,并且在一定程度上可以克服Gussain 函数缺少紧密性的缺点。
2.2 基于改进最近邻聚类的RBF 神经网络模型学习算法
实际上,最近邻聚类算法有尚待改进之处:需要比较长的训练时间、对于固定的网络结构难以确定其梯度下降的中心,此外其学习精度有待提升[6],文中采用了最近邻聚类中心选取结合梯度下降算法训练RBF网络参数的混合学习算法。
对于混合学习算法来说,其最近邻聚类可自动地聚类相关的样本,对隐层结构进行在线确定,通过梯度下降法来调整已经进行了在线确定的相关网络参数。算法中采用了一维数值形式,这样就减少神经网络的运算量并且提高了网络的训练速度和宽度参数。算法由两个部分构成:
(1)在线生成隐含层节点,建立RBF网络的拓扑结构。采用最近邻聚类算法选取初始中心,并且初步确定输出层权值。
(2)网络参数学习,它完成了校正中心、宽度和输出层权值等网络参数。采用梯度下降法调整(1)中获得的参数到最优值。
3 基于RBF 神经网络模型的结晶器液位系统设计
图3详细地描述了该控制系统,它主要包括下述2个部分:(1)神经网络PID控制器,该控制器利用该神经网络来进行在线学习过程,对参数进行自适应调整,从而达到智能化PID学习控制的目标[7]。(2)RBF辨识网络,用于结晶器液位系统的模型辨识,以便动态地观测结晶器液位系统的雅克比(Jacobian)信息,提供给神经网络PID控制器,实现其参数的自调整[8-9]。
根据图3可知,r 代表了液位设定值,y代表了其测量值,e 代表了上述二者之间的偏差值,u 代表了PID控制器所对应的具体输出,而yˆ则代表了RBF辨识网络所具体对应的输出。

图3 结晶器神经网络PID 控制系统原理图
结晶器液位系统的辨识网络采用基于改进邻聚类算法的RBF网络,该算法训练时间短,计算量小,具有很好的在线辨识能力。
将 u ( k ), y ( k ), y ( k- 1)作为RBF网络的输入,实现对结晶器液位系统Jacobian阵信息的辨识。Jacobian阵用准确的 ∂y ˆ /∂uˆ取代常规算法中符号函数近似值,从而神经网络PID控制器完成权值的调整。
此处可设 X= [ x1, x2, …, xn]T作为相关的输入向量集,而 H =[ h1, h2, …, hj]T则是该网络径向基向量,hj代表相应的Gussain基函数,则有下述关系:
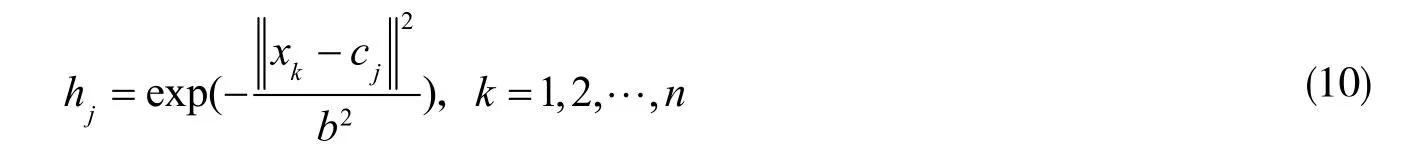
式中,kx 为输入矢量,jh 为第j 个隐层节点的输出,jc 为Gussain函数的中心矢量,b 为Gussain函数的半径。
在线学习步骤如下:
(1)对高斯函数自身的宽度b进行选择;以矢量 )(nA 来进行各类输出矢量的存放;以计数器 )(nB 来进行各类样本数量的统计。
(2)由首个数据 x1= ( x1, y1)起,降一个聚类中心构建于x1之上,然后可设 c1=x1, A(1)=y1,B(1)=1。从而可将唯一的RBF网络构建起来,而权矢量则表达如下: w1 = A(1)/B(1)。
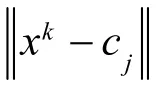
(4)在已经确定了网络的结构之后,可通过梯度下降方法来相应地调整节点基宽参数、网络输出权以及网络中心等,迭代算法如下:

式中,η —学习速率,α —动量因子。
Jacobian阵(即为对象的输出对控制输入的灵敏度信息)的算法为
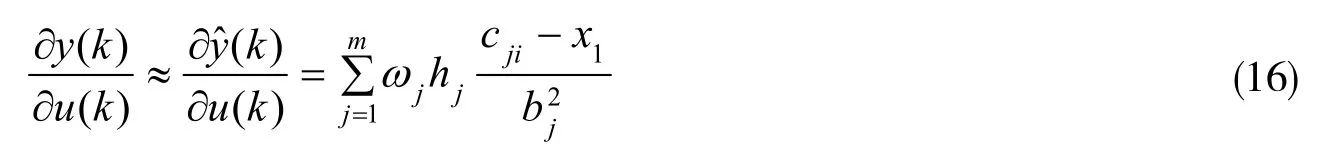
式中, x1= u(k)。
(5)计算所有输入样本的输出误差E,并利用梯度下降法调整各参数值。
(6)如果 E <ε,则训练结束,否则转到Step5。
(7)结束。
4 仿真研究
根据结晶器液位系统的特点,将结晶器液位系统简化为一个三阶系统,其传递函数为

首先要对结晶器液位控制模型离散化,在MATLAB 的命令窗口中键入如下命令:

离散化后的函数为
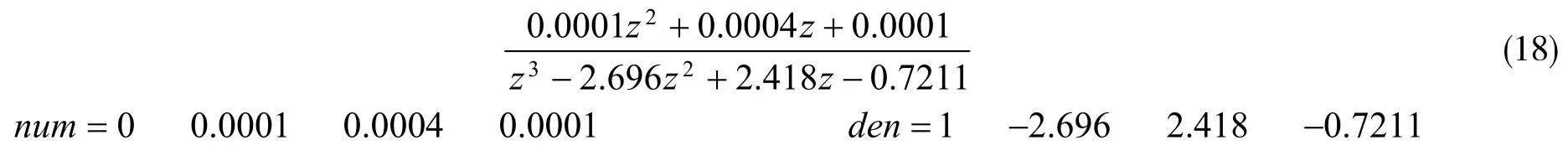
根据离散化的传递函数求出差分方程的结构:

对于结晶器液位模型,图4 呈现了传统PID 控制和基于最近邻聚类的RBF 神经网络PID 控制的阶跃响应曲线。图5 和图6 分别给出了智能PID 控制的Jacobian 信息曲线和误差曲线。
在仿真中结晶器液位控制目标设定为75 mm,RBF神经网络基函数的半径b取0.01。
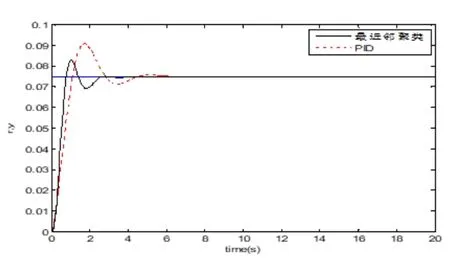
图4 系统阶跃响应仿真曲线

图5 Jacobian 信息曲线
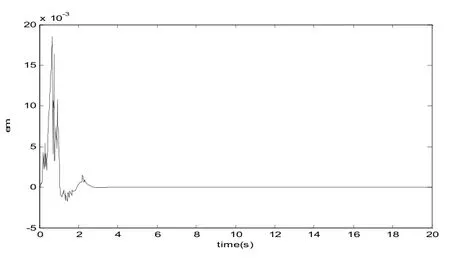
图6 智能PID 误差曲线
常规PID 控制算法中最大超调量为15 mm,上升时间为2 s,调节时间为8 s,稳态误差为0;智能PID控制算法:最大超调量为9 mm,上升时间为1 s,调节时间为4 s,稳态误差为0。
对比这二种算法所得到的相关仿真数据,发现它们具有较为接近的稳态误差,二者的调节时间只有4 s的差值,然而和常规PID 相比较,通过智能PID 来进行控制,将会有明显更小的最大超调量(低6 mm)。因此,通过系统各项性能指标的对比,充分显示了智能PID 控制具有较好的动态性能,符合工程实际要求。
由于结晶器液位的神经网络PID 控制算法中于引入了神经网络,系统的参数能够根据实际情况的需要不断调整变化。3 种参数作用根据系统过程的变化而变化,很好地调节了结晶器液位系统,使得系统在保持较快的响应速度的前提下,有效地抑制了系统的超调,并且缩短了调节时间,获得了较好的控制效果。
5 结束语
在进行PID 算法的参数整定之后发现,在对象没有出现变化的情况下具有良好的性能指标,由此可知它是比较理想的控制方法。但是对于真实的生产而言,由于往往会受不同因素所造成的影响,所以PID 参数无法取得最佳状态,而且当对象发生变化时,其性能指标将会受到较为明显的影响。在当前的工作中,所采用的神经网络PID 控制算法很好地融合了PID 控制算法与神经网络二者的优势之处,使得参数的在线调整过程具有更好的自适应性,促进系统稳定性的有效提升,因此控制效果较为理想。
