基于总变分JPEG2000 核磁共振图像解码算法

肖孝军，陈智斌

（1.贵州健康职业学院，贵州 铜仁 554300；2.昆明理工大学 理学院，昆明 650500）

随着大量的医学成像设备投入临床应用，核磁共振（nuclear magnetic resonance，MR）、电子计算机断层扫描技术（computed tomography，CT）以及超声波等数字医学图像在医学临床诊断中发挥着越来越关键的作用。首先医疗断层扫描对于感兴趣的身体结构部位往往输出16 至64 幅切片图像，超声和血管造影等检查甚至会生成3 min 以上的视频序列，这必然导致数字医学图像数据量快速增加。其次，大多数医学图像需要很长的保存周期，这使得数字医学图像需要更多的存储空间。此外，在远程医疗等应用环境下，要求在更窄的通信宽带条件下实现医学图像高保真度的传输，如不进行有效压缩，医学图像将占据大量的存储空间，对传输宽带造成很大的压力。最后，医学图像也属于自然图像范畴，其像素之间同样存在冗余性，具备压缩的可行性。

目前国内外流行的图像压缩标准是Joint Photographic Experts Group（JPEG）压缩标准，但是在有损压缩条件下，JPEG 为了减少图像存储空间，在压缩过程中往往丢掉一部分无关紧要的数据，而丢失的数据无法恢复，导致解码图像出现块效应、马赛克和Gibbs 等现象。JPEG2000 比较明显的优点是没有JPEG 压缩中的块效应，但是在对小波系数的高频部分进行量化时，导致高频数据一定程度的衰减，使得JPEG2000解码图像出现模糊失真，主要表现为压缩伪影、震荡等压缩痕迹。

为了提高低比特小波压缩的解码图像质量，国内外学者提出了多种后处理技术。Bourdon P 等[1]提出一种基于偏微分方程JPEG2000 解码迭代算法，此算法能够提高解码图像质量，但在高压缩比、迭代过多情况下平滑过甚，会磨平解码图像许多纹理成分。Fang 等[2]在JPEG2000 图像的空间域和每一个小波子带提出一种局部自适应Pentive 滤波，并得到一种新压缩损失计算方法。文献[3]提出一种边缘保护小波编码E-D模型，能够很好地消除边缘区域的压缩伪影。文献[4]提出一种原始图像伪影检测技术，并采用空间智能双边滤波抑制伪影技术。本文针对低比特JPEG2000 图像的模糊失真提出一种基于总变分后处理方案，提高了解码图像的质量，减轻了边缘区域的压缩伪影。

1 JPEG2000 标准

JPEG2000[5,6]分为编码端与压缩端，其编码器的框图如图1(a)所示。首先将离散变换应用于源图像数据。然后，在形成输出码流（比特流）之前，对变换系数进行量化和熵编码。解码器与编码器相反（图1(b)）。首先对码流进行熵解码，反量化和逆离散变换，从而得到重建的图像数据。

在编码端，JPEG2000 编码需要对原始图像进行预处理。首先，如果输入给编码端的图像内存较高，此时单一编码器不能处理整幅图像，将原始图像分割为非重叠的片，这些非重叠的片分别进行后续的编码操作。其次，在对子块进行离散小波变换（Forward discrete wavelet transform，FDWT）之前，通过减去相同量进行DC 电平移位。例如减去128，则一幅8 比特的图像的像素就变为区间[-127,128]范围内的系数。最后，执行色度空间转换，将RGB 色度空间转换为 YCbCr空间，本文考虑的是8 比特灰度图像，不考虑色度转换。

在量化之前对输入数据进行正交变换，是为了消除图像像素之间的统计相关性。在JPEG 标准中采用的是离散余弦变换，而JPEG2000 采用的是离散小波变换。Mallet 小波分解算法将图像分解成塔式结构，每一层小波分解形成4 个子带，即水平和垂直方向的低频子带LL、水平和垂直方向的高频子带LH、垂直和水平方向的高频子带HL、水平和垂直方向的高频子带HH。

进行小波变换后，通过降低小波系数的精度对每一个小波系数进行量化，当量化步长为1 且系数是整数时，JPEG2000 是无损压缩，反之是有损压缩，其量化过程是不可逆的，导致解码图像质量降低。其量化公式如式(1)所示

其中， ab（ i ,j ）表示子带b 的小波系数， qb（ i ,j ）表示子带b 的量化系数， Δb是子带b 的量化步长，sign 是符号函数。在量化过程中，量化步长越大，丢失的数据越多，解码图像质量越低，其计算公式如下：

对于量化步长可以分成两部分理解，2Rb将小波系数归一化到区间［ -1 /2,1/2］， 2-εb（1 + μb/211）表示真正的量化步长。

JPEG2000 解码端是压缩端的逆过程，首先进行熵解码得到量化系数，其次进行反量化操作得到反量化系数，其反量化公式如下：

其中，r 是任意选择的溢出参数，0 1r≤ ＜ ，其作用是尽可能减少因量化取整的不可逆性造成的压缩损失。最后对反量化系数进行逆小波变换（Inverse discrete wavelet transform，IDWT）得到解码数据。

2 基于总变分的JPEG2000 解码算法

2.1 总变分解码模型

核磁共振图像压缩（MRI）是医学图像处理中一个基本问题，因其成像扫描时间长，导致图像像素强度不均匀且空间分辨率不高，高压缩比情况下重建图像存在困难。熵编码是完全可逆的，JPEG 压缩痕迹主要是因本量化取整的不可逆导致解码图像质量下降，其退化模型可以理解为

其中，v 是被压缩系数，W 是小波变换，u 是相应的原始图像，η 是小波系数的压缩损失。文献[2]中，作者通过对多幅图像进行不同的压缩比实验发现，压缩损失η 近似地服从高斯分布。由于不同的压缩比，很难正确估计量化噪声的分布情况，但是通过大量仿真发现，可以用高斯概率密度函数去近似估计噪声分布，如图2 所示。

模型(4)是一个不适定反问题，无法从v 中保证u 的存在性、稳定性和唯一性，因此，有必要对求解方案添加约束使其正则化。考虑到二次正则化函数不能处理不连续图像的边缘区域，Rudin，Oshe 和Fatemi 提出一种总变分（TV）正则化模型[5]，结合对噪声进行分析将其修正为等式约束最优化问题

σ2是压缩损失的方差，引入拉格朗日乘子 λ ＞ 0，得到如下无约束的最优化解码（ROF）模型

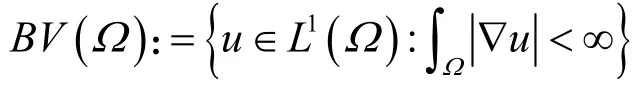
2.2 总变分离散模型

定义离散图像空间 X = RN×M，当u ∈ X，v ∈ X ，则内积为

同样定义图像对偶空间Y = X × X，若u ∈ Y，v ∈ Y，则相应的内积定义为

对于u ∈ X，定义 ∇： X →Y 为向前差分离散梯度算子， ∇ u = （ ∇xu ,∇yu ）'，其中 ∇xu ， ∇yu表示二维图像的水平与垂直方向的梯度算子

引理[6,7]存在u X*∈ ，p Y*∈ ，满足

其中，关于p 的最大问题是关于u 最小化问题的对偶形式，A 为线性算子，F*，G*分别是F 和G 的共轭函数。且上述最优解 u*∈X， p*∈Y与式(12)的鞍点问题最优解是等价的。

根据上述引理，则式(11)的对偶形式如下

式(13)中的散度算子 XY →:div 是梯度算子∇的伴随算子， div-=∇*，具体表达如下

其中，

综上，模型(11)对应地鞍点问题如下

2.3 模型求解

许多学者提出不同的算法求解TV去噪问题，例如对偶算法[8,9]、ADMM 算法[10,11]、牛顿方法[12]、bergman[13]、自适应投影算法[14]等。本文利用Chambolle 提出的原对偶算法[15,16]求解式(17)的鞍点问题，原对偶算法具体求解以下鞍点问题

其中， F: Y → ［0 ，+∞）和 G: X→ ［0，+∞）是凸函数，A 是线性算子，则原对偶算法的具体迭代格式如下

这里 ∂F , ∂G 分别是函数F 和G 的次梯度算子，（ I + τ∂ F ）-1表示邻近点运算符

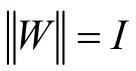
表1 基于总变分JPEG2000 图像解码算法

对于惩罚参数λ 的选择影响消除量化噪声与边缘信息的平衡，一种常见的办法是根据偏差原理选择λ 去匹配被压缩系数与小波系数的标准差2σ 。另一方面，希望每一次迭代使得式(5)中的2σ逐渐变小，所以把参数选择归为如下最优化问题

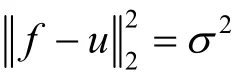
综上所述，基于总变分JPEG2000 图像解码算法如表1 所示。

3 数值实验

本节对两幅MR 图像（MRI-1、MRI-2）在不同压缩比条件下进行实验仿真，此外将TV-JPEG2000 解码算法与高斯滤波、中值滤波等去噪算法进行比较，用于实验的原始图像如图3 所示。迭代步长τ = 0.15，ρ = 0.25，最大迭代次数maxiter = 400，终止条件 tol = 10-4。用信噪比(SNR)量化图像质量。其定义如下

其中，u 是原始图像，*u 是解码图像，一般来说，SNR 越高，图像质量越好，与原图相似度越高。

在CR=10.6 情况下对MRI-1图像进行仿真实验，图4 为TV 函数曲线，图5 为对应的SNR 曲线，可以看出随着迭代次数的增大，目标函数不断减小并逐渐达到稳定值，从侧面说明本文算法的收敛性，SNR 值不断增加，说明本文算法的有效性。

图6 是不同后处理解码方法在CR=10.6 情况下MRI-1解码图像局部区域放大比较图。从图可以看出，JPEG2000 解码图像与原始图像相比出现明显的压缩痕迹，本文算法相对JPEG2000 解码图像、高斯滤波解码图像、中值滤波解码图像一定程度上提高了解码图像质量，减轻了压缩痕迹，视觉效果较好。对应的SNR 值可以从表1 查找，本文提出的算法其SNR 值为24.75，相比JPEG2000 解码图像提高1.06(dB)，高出中值滤波解码0.87(dB)，高出高斯滤波解码图像24.61(dB)。

图7 展示在CR=21.39 的情况下，MRI-2 不同方法的解码图像以及对应的边缘检测，此处用的是Sobel边缘检测算子。从图可以看出，本文算法不仅在图像边缘地区能够一定程度减轻压缩痕迹，同时也能够保护图像的边缘区域细节和纹理成分。从而说明本文算法能够减轻JPEG2000 解码图像因量化产生的量化噪声，相应各种算法的SNR 值可以在表2 中查找。

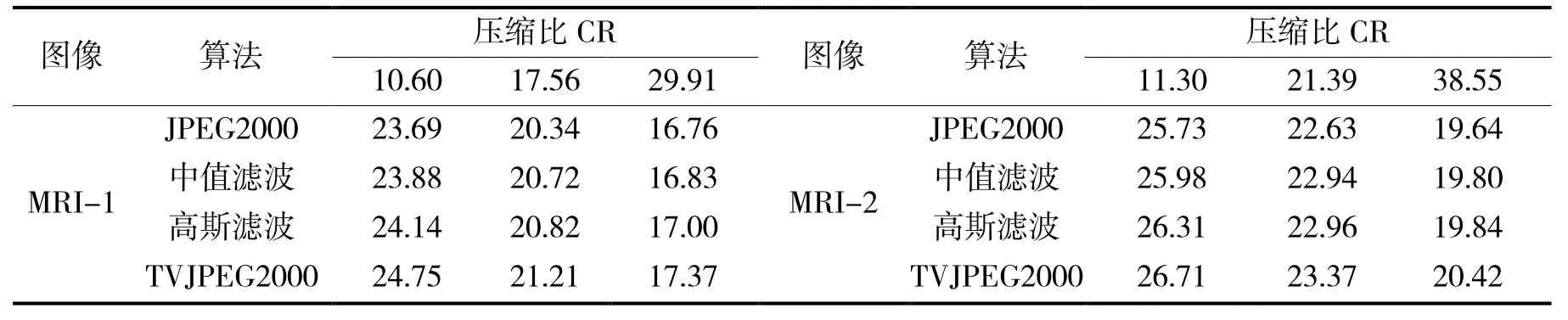
表2 不同算法在不同压缩比的SNR 值

4 结论

本文主要研究消除低比特核磁共振图像因JPEG2000 压缩造成的压缩痕迹问题，首先通过对JPEG2000压缩中量化噪声进行分析建立总变分ROF 最优化解码模型。其次利用原对偶算法求解提出的ROF 解码模型得到后处理核磁共振图像解码图像。最后为验证本文算法在消除压缩痕迹方面的有效性，对两幅MR 图像在多种压缩比情况下进行解码，并与传统的高斯滤波、中值滤波进行比较。数值实验结果表明，总变分JPEG2000 解码图像视觉效果较好，SNR 值相对较高，一定程度上消除了JPEG2000 解码图像的压缩痕迹。虽然总变分方法能够提高JPEG2000 医学解码图像的质量，但随着迭代次数的增加会磨平解码图像的细节信息，SNR 值会出现下降的问题，非局部总变分是解决这个问题的可行手段。此外，许多时候超声和血管造影等医学检查会生成三维多通道医学动态视频序列，接下来多通道三维总变分JPEG2000 医学视频解码是进一步研究的重要课题。