高强度钢筋活性粉末混凝土梁开裂弯矩试验研究

孙明德

（中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081）

活性粉末混凝土（Reactive Powder Concrete，RPC）作为一种新型的高性能水泥基复合材料，具有高强度、高韧性、高耐久性等优点［1］。HRB500 钢筋是一种性能优良的高强度热轧带肋钢筋，将HRB500 钢筋与RPC 配合使用可减少混凝土和钢筋用量，增大结构跨度，有利于发挥两者的优良性能。

RPC 中钢纤维的桥联作用可以增加其抗拉强度，延缓裂缝的产生。为掌握RPC 的开裂特性，文献［2］研究了24 m 超高性能混凝土预应力梁的抗裂性能；文献［3］建立了RPC 梁正截面抗裂计算模型；文献［4］通过6 根HRB400 钢筋RPC 梁抗弯试验建立了考虑受拉区拉应力的正截面开裂公式；文献［5］通过超高性能混凝土预应力梁抗弯试验，在JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》［6］中开裂公式的基础上引入抗裂影响系数，给出了超高性能混凝土梁开裂弯矩的建议公式；文献［7］对5 根HRB500钢筋RPC 简支梁进行了抗弯试验；文献［8-9］对大悬臂预应力超高性能混凝土薄壁盖梁和T形梁的抗裂性能进行分析，给出计算初裂弯矩和名义开裂弯矩的建议塑性影响系数；文献［10］对10 根活性粉末混凝土-普通混凝土结合梁的开裂性能进行了研究。目前，关于高强钢筋RPC 梁研究的试验样本较少，还需进一步研究。

本文制作了8 根HRB500 钢筋RPC 梁进行抗弯试验，研究配筋率对开裂弯矩的影响，并建立高强钢筋RPC梁开裂弯矩计算公式。

1 试验概况

1.1 RPC配合比及力学性能

RPC 材料包括：粒径为0.16～1.25 mm 的石英砂，42.5 普通硅酸盐水泥，微硅粉，高效减水剂，钢纤维。其中，钢纤维直径0.22 mm，长12～15 mm，抗拉强度≥2 800 MPa。活性粉末混凝土配合比见表1。

表1 活性粉末混凝土配合比 kg·m-3

RPC 试块采用先干后湿的搅拌工艺进行制备，标准养护24 h 后拆模，采用75 ℃蒸汽养护3 d，测得其抗压强度为120 MPa，轴心抗拉强度为6.9 MPa，弹性模量为4.53×104MPa。

1.2 试验设计

试验设计制作了8 根HRB500 钢筋RPC 梁，配筋率为0.87%～16.35%（表2）。纵向钢筋直径为12，16，20，25，32 mm，实测屈服强度分别为570，531，551，559，543 MPa。钢筋弹性模量为2.0×105MPa，架立筋均为2φ6。试验梁尺寸为2.0 m（长）×120 mm（宽）×250 mm（高），计算跨度1.4 m。试验梁浇筑36 h 后拆模，采用蒸汽养护3 d。

表2 试件配筋情况

1.3 加载方案和测试内容

参照GB/T 50152—2012《混凝土结构试验方法标准》进行试验，采用四分点对称分级加载，正式加载前对试件进行预压，试验装置见图1。

图1 试验装置

加载时测量开裂荷载、跨中挠度、混凝土应变和裂缝开展情况。位移计和混凝土应变片布置见图2。

2 试验结果

开始加载时梁体未产生裂缝，达到开裂荷载时，在梁体跨中或加载点附近产生了1～3 条裂缝，裂缝宽0.01～0.02 mm。荷载继续增大，裂缝数量增多，裂缝宽度增加并向梁高延伸。通过目测和混凝土应变片突变值来确定开裂弯矩Mcr。RPC梁的配筋率-开裂弯矩曲线见图3。

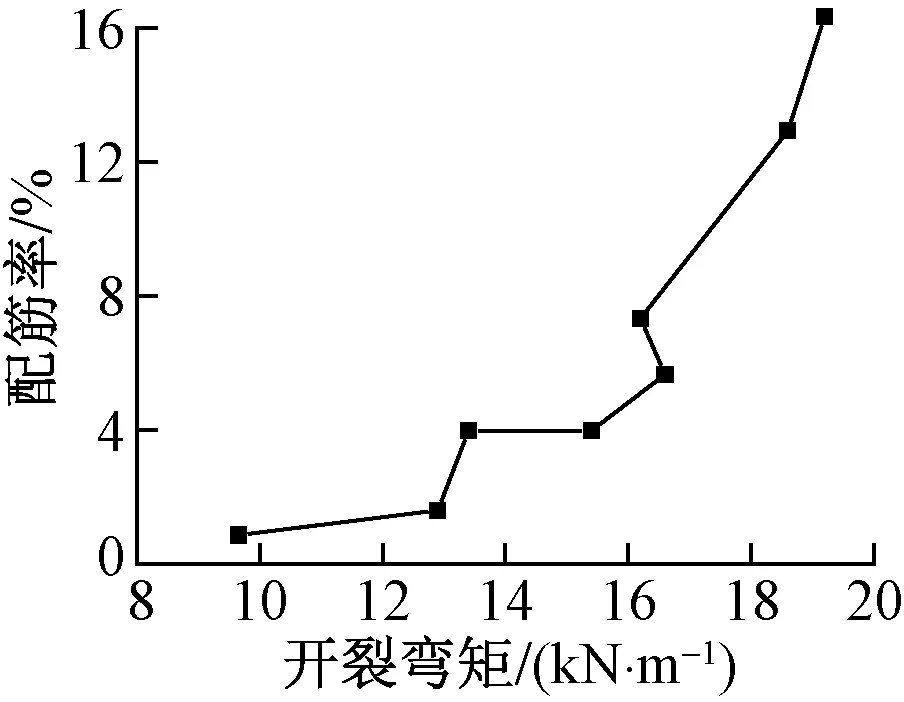
图3 RPC梁的配筋率-开裂弯矩曲线

由图3可知：随着配筋率的增大，开裂弯矩随之增大。原因是配筋率越高，钢筋换算为RPC 截面的等效截面越大，相当于增大了RPC梁的截面面积。

3 正截面开裂弯矩计算

3.1 开裂弯矩理论计算

RPC 梁开裂时的截面应力应变分布见图4。可知，开始加载时荷载较小，梁体处于弹性工作阶段。荷载继续增加，梁体的受拉区由弹性阶段进入塑性阶段，受拉区图形为曲线形，但抗压区仍处在弹性阶段。图中：σtc，εtc分别为初裂应变和初裂应力；σc，εc分别为压区边缘压应力、压应变；σt，εt分别为拉区边缘的拉应力、拉应变；εs为钢筋应变；h为梁高；b为梁的宽度；c为受拉边缘至受拉钢筋合力点的距离；h0为截面有效高度；x0为受压边缘到中性轴的距离；x1为受拉边缘到中性轴的距离；a为开裂高度；Ts为受拉钢筋拉应力的合力。

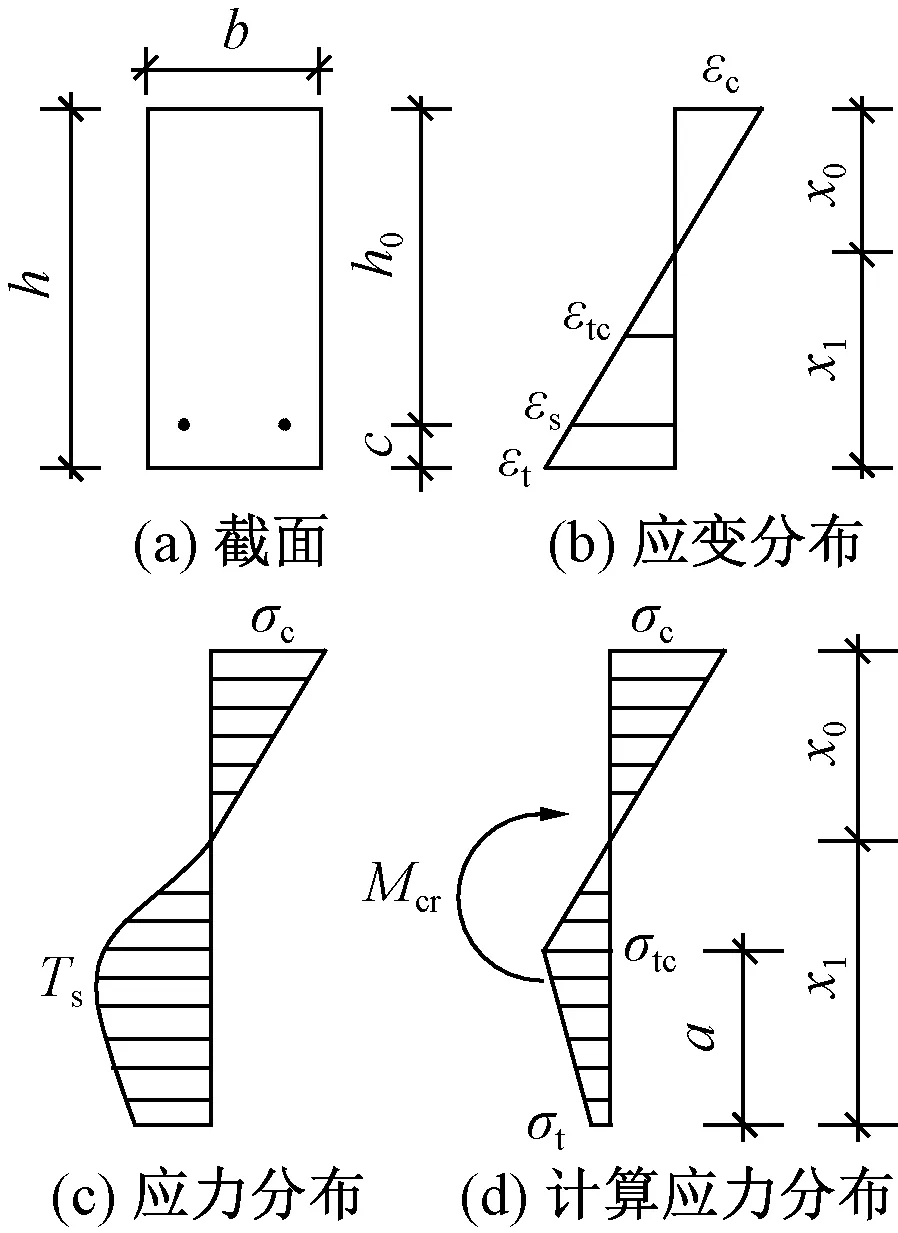
图4 截面应力应变分布

应力沿梁高分布，其计算式为

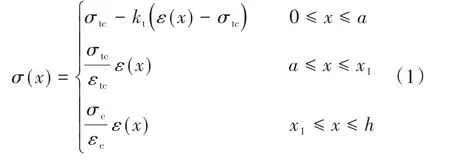
式中：σ（x），ε（x）分别为计算点处的应力、应变；kt=(σt-σtc)/(εt-εtc)。

根据力和弯矩的平衡条件可以求得Mcr，即

式中：σs为钢筋的应力；As为钢筋截面积。

3.2 截面抵抗矩塑性影响系数法

开裂弯矩Mcr由RPC 梁体承担的弯矩Mc和钢筋承担的弯矩Ms组成，采用截面抵抗矩塑性影响系数γm反映混凝土受拉区弹塑性发展程度。根据力的平衡条件可得：

式中：Ec为RPC 弹性模量；Es为钢筋弹性模量；α1为受拉区弹性部分与塑性部分的比值，由试验得到，取平均值为2.71；ft为RPC 的峰值拉应力；xc为受压区高度。

解得xc再对中性轴取矩得到Mcr，即

式中：W0为换算截面抗裂边缘的弹性抵抗矩。

截面抵抗矩影响系数γm为

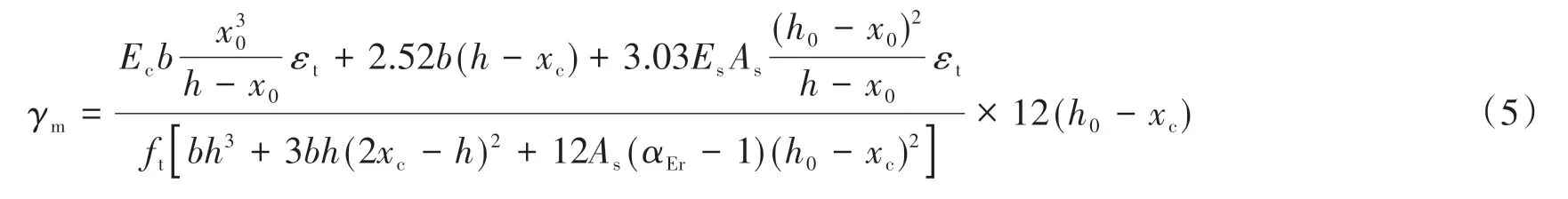
式中：αEr=Es/Ec。

采用式（4）和式（5）计算得到开裂弯矩和截面抵抗矩塑性影响系数，见表3。可知：①开裂弯矩试验值Mcr，t与公式计算值Mcr，1比值的平均值为1.09，变异系数为0.074，变异系数较小，说明RPC 梁采用截面抵抗矩塑性影响系数法的开裂弯矩计算公式适用良好。②随着配筋率的增大，γm随之增大。原因是配筋率的增大使得RPC 的塑化作用增大，间接提高了RPC 的抗拉强度。γm在配筋率为3.98%时趋于稳定。

表3 开裂弯矩与截面抵抗矩影响系数

由表3拟合得到γm的计算公式。

3.3 JTG 3362—2018规范开裂弯矩计算公式

采用理论计算方法和截面抵抗矩塑性影响系数法计算开裂弯矩较为繁琐。为了简化计算，参考JTG 3362—2018 中普通混凝土抗弯结构受拉区混凝土塑性影响系数γ及开裂弯矩计算公式推导RPC梁的开裂弯矩，其计算公式为

式中：S0为全截面换算重心轴以下部分面积对重心轴的面积矩；σpc为混凝土预压应力；ftk为混凝土轴心抗拉强度标准值。

实测开裂弯矩比JTG 3362—2018 规范计算值偏大，这是由于RPC 中掺入了钢纤维，其性能介于普通混凝土和钢之间，受拉区塑性变形程度比普通混凝土高，需要考虑钢纤维对受拉区塑性发展程度提高的贡献。因此，引入抗裂影响系数β，则式（7）变为

式中：λf为钢纤维含量特征值；ρf为钢纤维体积率；lf为钢纤维长度；df为钢纤维直径或等效直径。

根据开裂弯矩试验值对抗裂影响系数β进行回归分析，得到β=0.52，代入式（8）得到开裂弯矩Mcr，2，见表4。可知，Mcr，t/Mcr，2的平均值为1.10，变异系数为0.071，变异系数较小，说明RPC 梁采用修正的JTG 3362—2018规范开裂弯矩计算公式适用良好。

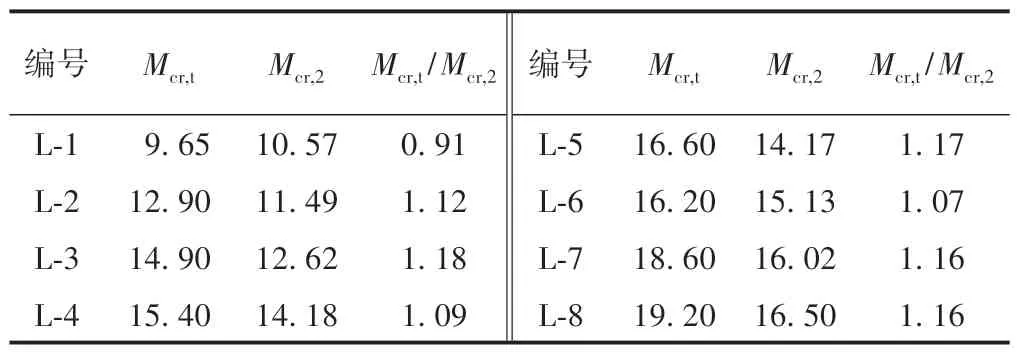
表4 Mcr,2与Mcr,t对比 kN·m

4 结论

1）RPC 梁的开裂弯矩随配筋率的增加而增大，提高配筋率有利于延迟裂缝的产生。

2）RPC 梁的截面抵抗矩塑性影响系数随配筋率的增加先增大后趋于稳定。

3）推导了考虑钢纤维对RPC 梁受拉区拉应力贡献的开裂弯矩计算公式，并对JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》中开裂弯矩计算公式引入抗裂影响系数，修正后公式的计算值和试验值吻合较好，采用修正公式计算开裂弯矩更简洁。