多模态优化问题的邻域低密度个体差分进化算法①
2021-03-19闵涛,杨胜
闵 涛,杨 胜
(西安理工大学 理学院应用数学系,西安 710054)
科学与工程领域的大多数优化问题本质上都是“多模态”的,这类问题被称为多模态优化问题,其特点是目标函数同时具有多个全局最优解或局部最优解.传统使用的求解方法在求解MMOPs 时须反复计算多次,才有可能找到不同的最优解,这样既费时又费力.因此,寻找可行有效的求解MMOPs的新算法一直以来备受广大科技工作者的关注[1-4].为此,许多被称为小生境的技术包括拥挤[5]、共享[6]、聚类[7]、物种[8]和种群拓扑[9]等被提出.小生境的主要思想是将整个种群划分为几个小生境(亚种群),每个亚种群集中于寻找一个或几个最优值.
差分进化算法(Differential Evolution,DE)[10]是由Storn和Price 在1995年提出的一种全局优化启发式算法.由于其简单、有效,已被用于处理各种各样的优化问题,例如全局优化问题[11],MMOPs[12],多目标优化问题[13]等.近年来,一些基于小生境的DE 变体[14-18]被提出以处理MMOPs,但是,这些方法在最优解数量大、维度高和复杂性高的时候效果往往不太理想.
本文提出了一种基于邻域低密度个体的差分进化算法(Low Density Points Differential Evolutionary,LDPDE)求解MMOPs.算法在每一代,首先使用密度峰值聚类的方法求得每一个个体的密度,然后,优先对邻域范围密度低于当前个体的目标个体进行突变操作,随着种群的进化,种群个体逐渐收敛到小生境中心,进化过程将会自动的从探索阶段转化为收敛阶段,进而平衡算法的探索与收敛能力.LDPDE 算法的主要特点有:(1)LDPDE是一种基于距离的小生境方法,它可以通过邻域范围内个体的密度变化达到算法探索与收敛之间的平衡.(2)提出了一种新的DE 变异算子,称为DE/low-density/1,该算子在算法的探索阶段可以寻找尽可能多的有效个体.
1 差分进化算法
考虑优化模型:

其中,X=[x1,x2,···,xn]为n维向量,Ω ∈Rn为求解区域,f(·)为目标函数.
差分进化算法是一种简单有效的全局优化启发式算法.与其他进化算法类似,DE 有4 个步骤:初始化、变异、交叉和选择.标准的DE 算法过程如下:
(1)初始化
首先,DE 从最小和最大界限约束的搜索空间内对个体进行均匀随机化,可以表示为:

(2)变异
初始化后,从当前种群中随机选择的个体经过变异算子产生突变个体vi.在标准DE 中,使用以下运算方法:

(3)交叉

其中,jrand∈{1,2,···,NP}是随机选择的索引,可确保ui至少继承突变个体vi中的至少一个分量.
(4)选择
选择运算符确定目标或实验个体是否进入到下一代.如果新的实验个体的函数值等于或小于目标个体的函数值,它将替换相应的目标个体.下一代xi,n+1中的目标向量为:

最后,DE 继续执行变异、交叉和选择运算符,直到满足终止条件为止.算法1 中以伪代码的形式给出了标准DE的算法过程.

算法1.标准差分进化算法(DE)输入:目标函数(最小值)f(x);比例因子F;交叉率Cr;种群大小NP;进化代数MaxIt.1)随机初始化种群 ;for n=1,···,MaxIt do X1=[x1,1,x2,1,···,xNP,1]2)3)for i=1,···,NP do()4)vi=xri1,n+F·xri2,n−xri3,n,5)uj i=■■■■■■■■■vji,rand 6)end for 7)for i=1,···,NP do 8)xi,n+1=■■■■■■■■■ui,f(ui)≥f(xi,n)xi,n,f(ui) 密度峰值聚类[19]是一种简单有效的快速聚类方法,由Rodriguez和Laio[20]通过发现潜在簇的密度峰值提出.对于每个数据点x(i),该算法都会计算其局部密度 ρ(i)以及与距其最近密度更大点的距离σ (i),由此可以得到每个数据点的孤立性.以下介绍密度峰值聚类的原理. 数据点x(i)的局部密度的定义如下所示: 其中,dij是第i个和第j个数据点之间的距离,dc是截止距离.对于截止距离dc,原始论文没有提供正确设置的有效方法.在文献[21]中,作者提出了一种基于潜在熵的方法,可以根据数据域自动设置.对于一个数据集x(i),i=1,2,···,n,计算第i个数据点x(i)的电势 ψ (i): 则熵H为: 其中,归一化因子z为: 现在只要找到使得H值最小的σ,记为σ′,即可得到截止距离dc.显然,dc的值一定处于min{‖x(i)−x(j)‖}和max{‖x(i)−x(j)‖}之间,对于简单的一维优化问题本文使用黄金分割法求得 σ,最后将临界值设置为dc=3· 为了解决多模态优化问题,许多策略被提出并将嵌入到DE 中.以下将简要介绍与DE 相结合的各种策略. (1)拥挤(CDE):文献[14]将拥挤方案和健身共享嵌入到DE 中,分别形成CDE 算法和SharingDE 算法.在CDE 算法中,对于每个子代个体,通过在父代种群中随机选择C个父代个体,然后将子代与该群体中最相似(欧氏距离最近)的父代进行比较.如果子代更好,它将取代该种群中最相似的父代个体.否则,子代个体将被遗弃.SharingDE 算法则利用共享方案来防止种群收敛到同一个高峰. (2)物种(SDE):在SDE 算法[15]中,根据个体的适宜性和小生半径r将整个种群分为几个物种.每个物种都有一个具有最佳适应性的物种种子,并且DE 运算符只在当前物种种群内执行.然后将生成的N个子代个体与N个父代个体合并为一个种群,从合并种群中选择N个最佳个体,形成一个新的种群. (3)聚类:Qu 等[16]提出了嵌入到CDE 算法和SDE算法中的邻域突变策略(包括NCDE和NSDE)中,DE 运算符在每个个体的欧几里得邻域中执行.遵循这一思想,Gao 等[17]提出了一种具有自适应策略(包括self-CCDE和CSDE)的聚类DE,它采用自适应参数控制来增强DE的搜索能力.Zhang 等[18]提出了一种新的基于位置敏感哈希的小生境技术以降低时间复杂度,并将其应用于NCDE 中,称为Fast-NCDE 算法. 以上这些方法在处理MMOPs 问题时已经显示出各方面的有效性,但它们也有一定的缺点.一方面,随着MMOPs 问题全局最优解的数量增加,这些方法将全部最优值点找到的机会就越小;另一方面,在解决具有高维度和高复杂性的MMOPs 时,几乎所有这些固定方法都会失效.因此,为解决高维度和高复杂性的MMOPs,许多其他基于DE的多模态算法被提出.Biswas 等[22]提出了一种新的信息共享机制,该机制使用本地信息矩阵来诱导有效的利基行为,称为LoINDE 算法(包括LoICDE 算法和LoISDE 算法).同时,他们还提出了一种新的以父代为中心的标准化邻域(PCNN)变异算子,以维持多个最优值,称为PNPCDE 算法[23].Wang 等[24]提出了是一种基于距离的小生境方法,称为MSTDE算法,通过DPR 策略切割少量大的加权边来形成多个小生境,平衡收敛性和多样性. 在本节中,我们将提出基于密度峰值的差分进化算法(LDPDE). 受文献[25]启发,提出一种用于多模态优化的新DE变异算子,称为DE/low-density/1.该算子的主要特征是它在当前个体邻域中随机选择密度低于当前个体的个体作为变异算子的目标个体,因此,目标个体可以被选择变异算子迁移到隔离区域.在典型的小生境方法中,同一山谷中的个体倾向于通过在山谷中下降聚集在一起.而在本文提出的方法中,个体积极地迁移到其他山谷.DE/low-densit/1 中使用的变异算子描述如下: 其中,是从{pnear(j) 当xi,n是xi,n的Nd1邻 域内密度最大的个体时,find(i)={pnear(j) 和互不相同,Nd3∈{1,2,···,NP−1}是用户指定的控制参数.Nd3=NP−1的情况与标准DE的差分向量取法相同.F2是比例因子. 如图1所示[25],图1(a)为邻域变异算子的行为特征,图1(b)为基于孤立个体的变异算子的行为特征.基于孤立个体的变异算子可以促使种群个体向孤立个体附近迁移,提高算法的多模态开发能力,而邻域变异算子只在小生境内进行,避免差分进化的贪婪原则带来的错误替换,提高算法的收敛性. 将以上两种变异操作结合形成的改进的变异算子描述如下: 随着种群的进化,{pnear(j)|j=1,2,···,Nd1}的值会趋于相等,find(i)为空的情况增多,基于孤立个体的变异算子的使用率下降,邻域变异算子的使用率提升,进而实现算法从探索阶段到收敛阶段的转变,平衡算法的探索与收敛能力. 图1 两种变异算子的行为特征 LDPDE的算法过程的伪代码的在算法2 给出. 算法2.基于邻域低密度个体的差分进化算法(LDPDE)输入:目标函数(最小值)f(x);比例因子F;交叉率Cr;种群大小NP;最大计算次数MaxFEs;邻域大小Nd1,Nd2,Nd3 1)随机初始化种群 ;n=0;X1=[x1,1,x2,1,···,xNP,1]2)3)while FEs<=MaxFEs do 4)n=n+1;5)for i=1,···,NP do 6)di,i=0;7)for j=i+1,···,NP do di,j=dj,i=‖xi,n−x j,n‖2;8)9)end for 10)end for 11)σ′=3·√12)2−1 argmin σ H(σ);for i=1,···,NP do (13))2)ρ(i)=∑j∈IS{i}exp−(dij dc ;14)end for 15)for i=1,···,NP do■■■■■■,find(i)非空■■■■■■,otherwise 16)vi=■■■■■■■■■■■■■■■■■xnear rp1,n+F1·■■■■■■xri2,n−x′ri2,n■■■■■■■■■xnear ri1,n+F2·vji,■■■■■■x′ri2,n−x′ri3,n 17)uj i=18)end for rand 本文采用了CEC2013 测试套件[26]中所有20 种常用的多模态测试函数来评估LDPDE的性能,该测试套件中的测试函数具有各种不同的特征,这使实验更加全面且令人信服.下面对这20 个基准测试函数作简要说明. F1:Five-Uneven-Peak Trap(1D),x∈[0,30].全局最优点数量为2. F2:Equal Maxima(1D),x∈[0,1].全局最优点数量为5. F3:Uneven Decreasing Maxima(1D),x∈[0,1].全局最优点数量为1. F4:Himmelblau(2D),x1,x2∈[−6,6].全局最优点数量为4. F5:Six-Hump Camel Back(2D),x1∈[−1.9,1.9],x2∈[−1.1,1.1].全局最优点数量为2. F6,F8:Shubert(2D,3D),xi∈[−10,10]D,i=1,2,···,D.全局最优点数量分别为18和81. F7,F9:Vincent(2D,3D),xi∈[0.25,10]D,i=1,2,···,D.全局最优点数量分别为36和216. F10:Modified Rastrigin-All Global Optima(2D),xi∈[0,1]D,i=1,2,···,D.全局最优点数量为12. 其中,k1=3,k2=4. 剩下的10 个函数为4 个复合函数在不同维度大小的情况,把4 个函数简称为CF1,CF2,CF3和CF4,定义域均为xi∈[−5,5]D,i=1,2,···,D.复合函数的具体定义可以参考文献[26]. F11:CF1(2D).全局最优点数量为6. F12:CF2(2D).全局最优点数量为8. F13,F14,F16,F18:CF3(2D,3D,5D,10D).全局最优点数量为6. F15,F17,F19,F20:CF4(3D,5D,10D,20 D).全局最优点数量为8. 将LDPDE 与几种基于DE的多模态算法进行比较,包括CDE 算法,SDE 算法,NCDE 算法,NSDE 算法,LoICDE 算法,LoISDE 算法,PNPCDE 算法,Fast-NCDE 算法和MSTDE 算法.这些算法横跨从2004年到2019年的时间间隔.此外,为了具有可比性,所有对比算法的参数配置都与原始论文中的设置相同. LDPDE 中的放大系数F1和F2分别设置为0.9和0.5,交叉速率Cr设置为0.9,Nd2和Nd3分别为5和15.针对不同的函数参数Nd1、种群规模N和最大计算次数MaxFEs设置如表1所示. 表1 参数设置 LDPDE 中的种群规模、最大计算次数MaxFEs和比较算法的结果参考自文献[24].所有的结果都是在同一测试套件中使用相同的MaxFEs下得到的,每种算法均运行51 次以进行统计并避免随机性. 对于给定的MaxFEs在精度水平ε=10−4下,使用峰值比(Peak Ratio,PR)和成功率(Success Ratio,SR)评估算法的性能.峰值比为找到的全局最优解个数与所有全局最优解数之比,成功率为所有全局最优解被找到次数与实验总次数之比.PR和SR 均为0 到1.0之间的实数,数值越大说明算法效果越好.当PR和SR 均为1.0 时说明算法每次都能找到函数所有的最优解. 表2列出了LDPDE 与其他多模态算法在F1-F20上PR和SR的详细比较结果.为了结果清晰,最佳PR果用黑体标出.符号"+"、"−"和" ≈"分别表示LDPDE的性能“显著优于”,“显著低于”和“与对比算法相当”.以CDE 算法为例,本文算法在13 个函数上优于CDE算法,0 个低于CDE 算法,7 个与CDE 算法结果相当. 表2 LDPDE 与其他多模态算法在F1-F20 上PR和SR的详细比较结果 从表2可以看到LDPDE 在所有函数上都表现很好.对于简单函数F1−F5和具有众多全局最优值的函数F6−F10,LDPDE 除了对于具有216 个全局最优点的F9之 外的其它九个函数的PR值 全部达到了1.0,也就是说LDPDE 算法在这九个测试函数上每次都能找到函数所有的最优解,虽然F9的PR值只有0.587,但也明显优于于其它算法.对于最后的十个高度复杂多模态函数F11−F20 (其中F11−F15为低维,F16−F20为高维),LDPDE的性能几乎处于绝对的优势地位,只有少数几个算法在一到两个函数可以与本文算法性能相当,这进一步验证了LDPDE 在解决高度复杂的MMOPs方面的可行性和有效性. 多模态函数F1−F20的收敛曲线如图2(a)-图2(d)所示,目标函数误差值为每个函数运行51 次所得每一代最小值的平均值与函数极值之差的绝对值,为方便观察,将纵坐标取以 10为底的对数(值为0时曲线未画出).图2(a)中函数F1的曲线极短,这是由于F1函数简单,算法在很少的进化代数就计算得出最优函数值导致的.而函数F3的计算精度达到1 0−7之后很难继续改进.其他18 个函数收敛曲线呈现明显的收敛趋势,虽然随着函数复杂程度的提高收敛速度减慢,但收敛趋势稳定,收敛精度也都能达到1 0−18,这也体现出本文算法在高维复杂多模态函数优化上的优势. 总之,LDPDE 在所有20 个函数上与CDE,SDE,NCDE,NSDE,LIPS,LoICDE,LoISDE,PNPCDE,self-CCDE,self-CSDE,fast-NCDE和MSTDE 算法相比PR值都优于或相当于对比算法.收敛性分析结果表明,LDPDE 可以在搜索与收敛之间找到良好的平衡,具有解决MMOPs的潜力. 图2 目标函数误差值收敛曲线 针对多模态优化问题,本文提出了一种基于邻域低密度个体的差分进化算法LDPDE,它可以通过邻域范围内个体的密度变化达到算法探索与收敛之间的平衡,有效提升了算法的可靠性和收敛速度,结合新提出的DE/low-density/1 变异算子,使得算法在探索阶段可以寻找尽可能多的有效个体.在CEC2013 多模态基准测试的实验结果表明,LDPDE 对比其它多种基于DE的多模态优化算法具有更好的性能,显示了LDPDE在求解多模态优化问题上的优势.
2 准备工作
2.1 密度峰值聚类




2.2 其他多模态优化算法
3 基于低密度的差分进化算法
3.1 基于孤立个体的变异算子

3.2 邻域变异算子

3.3 改进的变异算子
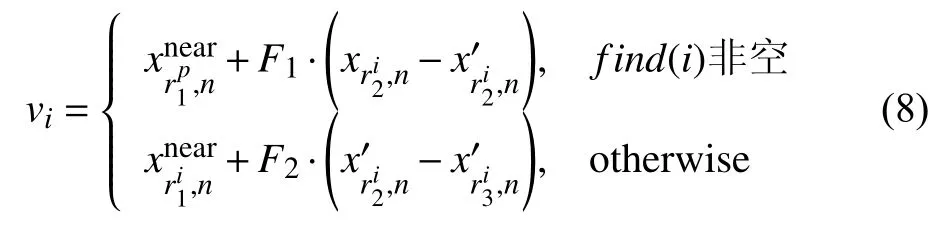


4 实验与讨论
4.1 测试函数


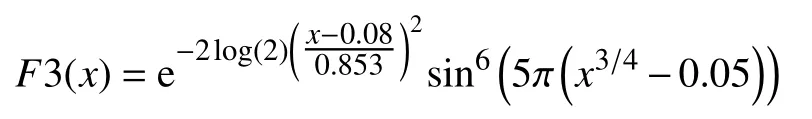





4.2 参数设置

4.3 结果与讨论


5 结论与展望
