面向自动参数调优的动态负载匹配方法
2021-03-18
(武汉大学计算机学院,武汉 430072)
0 引言
数据库参数调优是一项维持或提升数据库性能的重要工作。由于数据库的性能受到多个参数共同影响,再加上可调参数数量、数据库体量和业务量的剧增,导致传统基于人力的参数调优越来越困难。随着自治数据库[1]技术的发展,数据库自动参数调优技术成为了解决这一难题的主要选择之一。
得益于机器学习技术的发展,现在已经出现了一些数据库自动参数调优方法[2-3]和系统[4-5],例如OtterTune[2]。在这些方法中,对调优目标系统的工作负载的了解是进行调优的基础。只有准确地描述负载,才能找到与目标负载最相似的历史负载,从其对应的参数配置寻找目标负载的最优配置方案。
对负载的了解依赖于负载的描述、匹配以及预测方法。数据库负载的描述主要有两种方式:1)用负载所含的操作描述,例如SQL(Structured Query Language)语句的到达率[6-9]、SQL 到达率与数据库信息的结合体[10]、每秒事务总数与事务类型的混合率[11];2)使用运行时数据库中各项资源利用率或性能指标描述,例如系统资源(内存、中央处理器(Central Processing Unit,CPU)和磁盘等)的利用率、数据库资源(缓冲区、锁等)的利用率[12-15]、并发用户数和响应速度[16]。
虽然这些描述方式各有优势,但都是以点概面地以负载在某个时间点的表现来概括其整体特征,而忽视了负载会随时间变化的动态特性。这种以偏概全的描述方式实际上制约了调优方法的有效性和准确性。
针对现有自动调优工具中采用的负载描述和匹配方法无法捕捉负载动态特性的问题,本文提出了一种动态负载描述方法以及相应的匹配算法,并将其应用于OtterTune 上,并通过实验验证了其有效性。本文的主要工作总结如下:
1)提出了一种可捕捉负载动态特征的描述方法来更准确地刻画负载;
2)提出了一种基于动态时间规整(Dynamic Time Warping,DTW)[17-18]的动态负载对齐方法,并以其为基础提出了基于数据对齐的动态负载匹配算法;
3)将上述方法应用于OtterTune 中扩展形成了基于动态负载的自动参数调优工具D-OtterTune(Dynamic workload based OtterTune),并利用实验验证了本文方法的有效性。
1 动态负载描述和匹配
自动参数调优第一步需要得到目标数据库当前的负载特征。数据库的负载变化形态各异,无论是联机事务处理(OnLine Transaction Processing,OLTP)还是联机分析处(OnLine Analytical Processing,OLAP)型业务,负载变化是非常频繁的。图1 给出了两种以数据库内部性能指标描述的负载,从中可以看到,如果以t=6 min 采集的数据来表示负载,则workload1 和workload2 会被视为相同。事实上,workload1表示的负载比较稳定,而workload2 表示的负载波动较大,采用静态负载描述无法真正区分不同的负载。
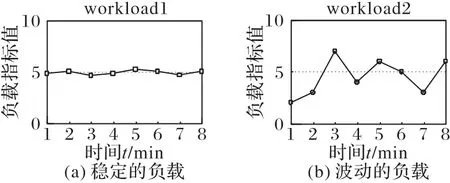
图1 两类不同特征的负载Fig.1 Two workloads with different characteristics
为了更准确地描述负载,本文针对负载的动态变化特性,基于多次采样思想,在观察期内进行多次性能数据采集,用这些连续的性能切片来刻画负载的动态变化。
首先引入Dialogue的概念来表述观察期,Dialogue是一次观察期间多个采样点的集合,可表示为式(1):
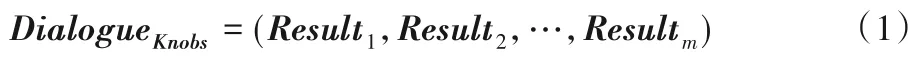
其中Result为采样点,Result表示为二元组其中Knobs为配置参数值向量,Metrics是目标数据库的内部性能指标向量,同一观察期中采样点的Knobs向量相同。观察期中的Metrics序列则反映了目标数据库上负载的变化,其时序特性使得上述动态负载描述方式能够更准确地描述负载的动态特征和波动情况。
在实际应用中,由于同一Dialogue中的采样点具有相同的Knobs部分,且Metrics部分中的一些分量值也可能相同,因此可以在动态负载描述数据的传输、存储过程中采用适当的压缩技巧和算法来减小数据量。如果将Dialogue中的Knobs部分进行压缩,理论上可以达到将近50%的压缩率,可以有效缓解由于多点采样带来的通信量和存储的膨胀。
2 动态负载匹配算法
在自动参数调优方法中,取得当前负载的动态描述之后,需要进行负载匹配,从而得到合适的配置参数作为参数优化探索的基础。负载匹配的准确度密切影响着性能预测、配置推荐等后续操作的精确度。对于带有时序特征的动态负载数据匹配,直接基于欧氏距离的向量相似度计算方法不再适用。为解决这一问题,本文提出了一种基于DTW 的动态负载数据匹配方法。
2.1 动态时间规整算法
在基于单点采样的负载匹配中,只用单个点的负载数据与历史负载数据进行相似度的比较,所以两点之间计算欧氏距离时,并不存在波形的相位偏移问题。在采用了动态负载描述后,则是由多个形式的采样点来表示负载形态,这些具有时序特征的连续采样点可视为负载变化的过程。尽管采集的数据是离散点,但这些采样点序列仍具有波形的部分特征,如周期、峰值和频率。
对动态负载描述进行相似性匹配,需要比较两个时间序列之间的相似性。简单地把欧氏距离用于采样点序列匹配存在以下局限性:1)两个序列的长度必须长度相等。由于需要计算两个序列中每对对应点之间的差值平方和来比较相似性,因此必须保证两个序列上的点之间一一对应。2)两个序列在形状的变化上具有位置一致性,即两个波形不能存在相位差和峰值的偏移,否则相似性的计算结果会有较大偏差。如图2 所示,两个峰值点a、b本应是对应的,但由于峰值偏移导致峰值点a与b'对应,显然在这种情况下使用欧氏距离计算会使序列匹配的精度下降。
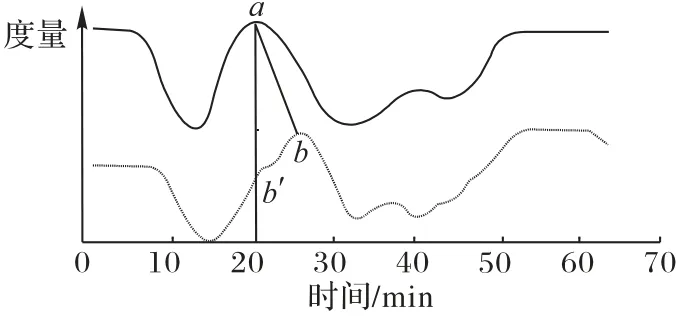
图2 两个不同时序长度的峰值点之间的偏移误差Fig.2 Offset error between peak points of two different time-series lengths
动态时间规整(DTW)算法基于动态规划的思想,解决了传统欧氏距离匹配上的限制问题。DTW 算法能通过动态规划,找到在两个匹配序列中和位置最相匹配的点。
如图3 所示的峰值偏移,目标序列中的峰值点通过使用DTW 算法能够找到匹配序列中对应峰值的位置,并将两个点作为距离计算的对齐点。这样便解决了相位、峰值偏移的问题;但单纯使用DTW 算法无法过滤噪声,需要配合使用波形变换来预处理降噪。
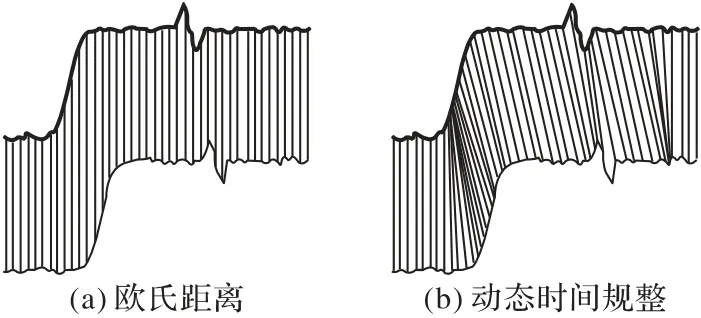
图3 欧氏距离计算和动态时间规整算法Fig.3 Euclidean distance calculation and DTW algorithm
2.2 基于DTW的动态负载数据对齐
相位和峰值偏移会导致动态负载数据的匹配准确率低下。在进行匹配之前,首先需要对历史收集的动态负载数据进行对齐,才能保证训练集的准确性和模型的精确度,从而保证后续匹配操作的准确性。
本文采用了一种基于DTW 思想的动态负载数据对齐方法来处理历史动态负载数据,其过程如算法1 所示。算法输入是历史负载数据集C,输出是Metrics序列对齐后的数据集SC。算法中先选取一条长序列作为对齐标准,之后主要分为2 个步骤:1)首先基于DTW 算法进行Metrics序列相似度对齐,使用最大前缀匹配策略(循环补齐左平移);2)然后将对齐后的数据集中长度不一的序列进行长度规整。对于长度不够的序列,可以拷贝其他标准长度序列的尾部来进行长度补齐,这样可以尽可能保留负载描述的细节。
算法1 基于DTW的动态负载数据对齐。

数据对齐开销较大,对于数据集中的每个Metrics序列都要进行平移和计算。从算法1中可以看到,假定数据集中有k次观察的Dialogue数据,最长的序列采样n次,那么算法时间复杂度如式(2)所示:

其中:n对应于每个序列进行平移的次数,n2为每次平移之后进行DTW 算法匹配的时间复杂度,最后乘以数据集中序列的个数k。理论上,k是远远大于n的,所以其复杂度是O(k*n3)。不过,数据对齐是对历史数据集定期进行的预处理,并不需要太高的实时性,因此这种复杂度仍处于可接受的范围。
2.3 基于数据对齐的动态负载匹配
在进行当前负载与历史负载的匹配工作时,可以直接使用DTW 算法来计算负载中Metrics序列的相似度。虽然DTW能够解决一定的相位、峰值的偏移问题,但是会导致部分数据无法匹配的问题。
如图4 所示,X和Y序列之间存在一定的相位和峰值偏移,DTW 是基于时序序列的匹配,强调从前到后的序列化匹配过程。从图4来看,X序列的前几个点会直接开始匹配Y序列中间部分点,Y序列完结后会导致X之后的序列都只能在Y序列的最后一点上进行复制匹配,而无法匹配Y序列中的前几个点。
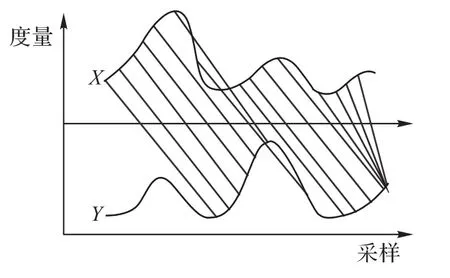
图4 DTW算法的部分数据对齐Fig.4 Partial data alignment of DTW algorithm
DTW 方法虽然能够探索两个序列之间的相似度,但是需要两个序列的开始和结束的统一性。因此,方法DTW 算法可以用于不规则序列匹配,但是会因为时序交叉损失部分序列的匹配精度。
本文针对动态负载,提出了一种基于数据对齐的匹配算法,如算法2所示。
算法2 基于数据对齐的动态负载匹配。

算法2 中使用序列循环补齐左平移来减少序列之间的相位差值。如图5所示,Y曲线尾部虚线位置为左侧序列的循环补齐,序列循环补齐之后,时序交差的大部分头尾部分能够得到最大限度的匹配。由于采样粒度的问题,并不能保证两段序列采样的开始点和结束点都完美一致,但是这已经尽最大限度扩大了序列中部分匹配的长度,减小了因序列交错导致不匹配而产生的误差。

图5 循环补齐平移后的数据对齐Fig.5 Data alignment after cyclic complementary translation
3 实验分析
为了测试基于DTW 的动态负载匹配方法对数据库自动参数调优问题中的效果,本文以OtterTune 为基础,将其负载描述和匹配方法替换为本文提出的动态负载描述和匹配方法,形成了一个衍生系统D-OtterTune。OtterTune 和DOtterTune 架构模型相同,使用单独的外部调优系统,调优系统和目标数据库系统分离。外部调优系统优点就是在繁重的分析处理中不会干扰到数据库本身的业务负载。然后部署一个GreenPlum 作为目标数据库系统,利用OtterTune 和DOtterTune 对其进行参数调优,对比最后的调优性能以及调优过程中负载匹配的准确度。
实验中采用3 台服务器构建测试集群,1 台作为Master 节点,其他2 台作为Segment 节点,服务器配置均为Intel Xeon E5 2603,16 GB 内存,1 TB 固态硬盘。各节点操作系统采用Ubuntu 16.04,GreenPlum版本为6.0。
3.1 实验方案
实验中采用TCP-H测试基准产生对测试集群的负载。设置测试数据量为30 SF(Scale Factor)。TCP-H 共有22 条压力查询语句,随机使用这些查询语句对测试数据库进行并发访问,其中随机选取时间段增加/减少并发度以形成负载测度上的波动。
在实验中进行了两个方面的对比:
1)在D-OtterTune 中将本文匹配方法与传统基于欧氏距离的匹配方法进行比较。进行两次完整的配置推荐过程,一次是采用传统的非数据对齐、基于欧氏距离匹配算法来推荐配置;另一次是将数据集数据对齐之后,采用DTW 的动态序列匹配算法进行匹配后推荐的配置。通过推荐的效果来展示本文提出的动态负载匹配方法的效果。
2)分别用OtterTune 和D-OtterTune 对同一个负载进行调优,比较两者推荐的参数配置产生的性能。在这个实验中,还增加了一个对照系统N-OtterTune,该系统在OtterTune 中采用动态负载,但不做数据对齐且采用传统的欧氏距离匹配方法。
3.2 数据对齐的效果测试
在对数据对齐效果的测试中一共采集26 个Dialogue对话,每次采样的时序深度为20 次,观察期长度为20 min,即1 min一次性能采样,一共得到了16组长度为20的时序序列。由于每个时序点是一个Metrics向量,为了观察数据对齐的效果,使用Metrics中变化明显的blkshit和blksread元素组成的命中率来表示数据对齐的效果:

图6 展示了测试中采集到的3 个比较有代表性的命中率折线图,其中横坐标为时序点,纵坐标为命中率。由于采样点的粒度和开始采样时间的不同,图6 中命中率变化折线存在明显的相位和峰值偏移。进行数据对齐之后,这3 个序列的情况如图7所示。
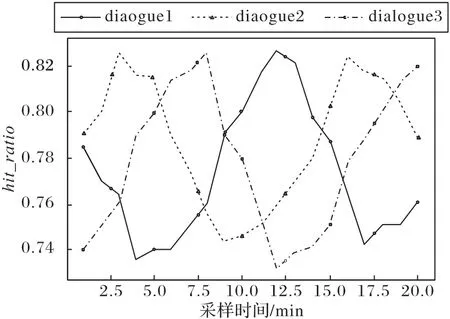
图6 数据对齐前3条代表性的命中率曲线Fig.6 Three representative hit ratio curves before data alignment
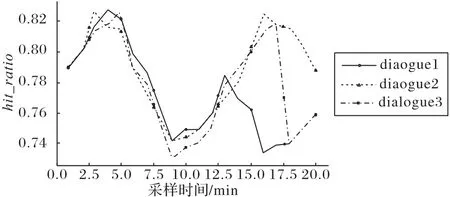
图7 数据对齐后的3条代表性命中率曲线Fig.7 Three representative hit ratio curves after data alignment
3.3 总体效果测试
为了对比采用动态负载前后自动参数优化方法的推荐结果,实验中采用3.2 节中采集到的数据集,利用OtterTune 和D-OtterTune 完成了3 次完整的配置推荐过程:第1 次采用OtterTune 推荐(origin metrics),第2 次采用N-OtterTune 推荐(normal metrics),第3 次采用D-OtterTune 推荐(align-data metrics)。
在得到推荐配置之后,分别将3 种推荐配置应用于同一个目标集群,并进行TCP-H 压力测试采集性能表征数据。为了可视化对比结果,同样采用hit_ratio 来代表推荐配置的性能指标,如图8所示。

图8 总体性能比较Fig.8 Comparison of overall performance
从图8 可以发现,与OtterTune(origin metrics 折线)相比,N-OtterTune(normal metrics 折线)在性能上并没有明显提升。而进行了数据集对齐且采用了本文提出的动态负载匹配方法之后,D-OtterTune(align-data metrics 折线)对负载的拟合精度得以提升,以hit_ratio 为代表的性能指标在整个观察期间幅度都有稳定提升。提升率达到3%,在数据密集型应用中,对整体业务性能可以产生明显影响。这也进一步证明了本文提出方法的有效性。
4 结语
针对数据库的自动参数调优问题,本文分析了工作负载的静态描述所存在的问题,提出了一种动态负载的描述方式,能更准确描述工作负载变化情况。针对动态工作负载序列匹配存在的序列不规则的问题,本文基于DTW 算法提出了一种使用数据对齐思想的数据聚合方式。然后提出了一种基于数据对齐的动态负载匹配算法,并将其引入自动参数调优系统OtterTune 中形成了D-OtterTune。最后通过实验验证了以上方法的有效性。
对于稳定和周期性变化的负载,可以很好地利用历史数据集进行学习并推荐配置。但当在递增型负载的模型下,当前性能的采集并不能代表将来的负载形态,所以不能直接使用历史库中数据的配置来进行推荐。本文未来的工作将探索一种能够利用当下采集的负载变化趋势,来对将来的负载进行预测的学习模型,然后根据预测的负载形态来进行配置推荐。
