基于U-D 分解卡尔曼滤波地下水污染源溯源辨识

贾顺卿,卢文喜*,李久辉,白玉堃 (1.吉林大学地下水与资源环境教育部重点实验室,吉林 长春 130012；2.吉林大学新能源与环境学院,吉林 长春 130012)

地下水作为人类生存与社会发展必要的自然资源,近年来遭受的污染问题愈发严重.地下水污染难以监测,不易治理.地下水污染溯源识别是地下水污染修复与治理过程中的重要一环,能提供污染源空间分布、污染物释放历史等信息,为其治理提供参考依据.

卡尔曼滤波是求解地下水污染反问题的一种有效方法[1].卡尔曼滤波作为一种最优状态估计方法,可以应用于受随机干扰的动态系统[2-3]. Herrera[4],Schmidt 等[5]应用卡尔曼滤波对地下水水质监测网进行时空优化;Dokou[6]尝试使用卡尔曼滤波创建一个最优的搜索策略,使用最少的水质样本来识别DNAPL 来源[6],Jiang 等[7],江思珉等[8-9],顾文龙等[10]应用基于卡尔曼滤波技术和模糊集理论识别污染羽的方法.常规卡尔曼滤波可能出现矩阵协方差非对称或者负定的情况[11-12],崔尚进将卡尔曼滤波协方差矩阵进行U-D 分解,提高了卡尔曼滤波的稳定性[13].Chen 等[14], Xu 等[15-16]使用集合卡尔曼滤波对二维确定性含水层中的污染源进行了溯源辨识[14-16];场地信息存在不确定性[17-18],白玉堃等[19]采用灵敏度分析筛选出灵敏度最高的参数作为随机变量进行污染源反演.

结合前人研究,本文运用U-D 分解卡尔曼滤波识别污染源的个数与位置,在此基础上建立优化模型,采用克里格插值法建立替代模型并嵌入优化模型,运用遗传算法求解优化模型得到污染源源强.

1 研究方法

1.1 技术路线

图1 污染源反演技术路线Fig.1 Flow chart of contamination source identification

首先应用U-D 分解卡尔曼滤波反演污染源的个数与位置.在现场调查与动态监测的基础上,结合专家意见初步估计污染源潜在的个数、位置以及初始权重,构建地下水溶质运移模拟模型.考虑场地信息存在不确定性,对场地参数进行灵敏度分析,筛选出灵敏度最高的参数作为随机变量,其余参数作为确定型变量.给出随机变量一个取值范围,由拉丁超立方抽样生成参数随机场,采用蒙特卡罗法将参数随机场输入模拟模型生成溶质浓度场库,结合各潜在污染源初始权重计算得到初始综合浓度场与误差协方差矩阵.对误差协方差矩阵进行U-D 分解,结合采样点数据运用U-D 分解卡尔曼滤波对污染浓度场和潜在污染源权重进行更新,权重稳定后判断污染源的个数与位置.

在识别出污染源个数与位置的基础上建立优化模型,进行污染源释放强度反演.以污染物监测浓度与模拟计算浓度拟合误差极小化为目标函数,污染源释放强度为待求变量,替代模型作为优化模型等式约束条件,同时考虑源强上下限等约束条件,建立非线性规划优化模型,运用遗传算法求解优化模型反演出污染源释放强度.为了减小求解优化模型时调用模拟模型产生的运算负荷,建立溶质运移模拟模型的克里格替代模型.

1.2 灵敏度分析与浓度场库建立

灵敏度分析可反应模型输出对参数变化的敏感程度,本文采用Morris 全局灵敏度分析方法评价参数变化对模型输出的影响,选出影响程度最大的参数进行研究.Morris 设计采用“一次只改变一个参数”的抽样取值方法,轮流计算各参数的目标函数值,从而得到各个参数全局灵敏度及参数间相关性和非线性的定性描述[20-21]:

把研究区用网格剖分,将筛选出的参数进行拉丁超立方抽样得到n 组随机变量参数场,只考虑一个潜在污染源时,输入模拟模型得到对应的n 组溶质浓度场,m 个潜在污染源共m ×n 组.计算每个网格上参数场取不同值时浓度值的均值,就得到了该污染源的均值浓度场.在同一随机变量参数场下,m个污染源的溶质浓度场按照初始权重进行加权叠加得到叠加浓度场.将m 个污染源的均值浓度场按初始权重进行加权叠加得到初始综合浓度场.

1.3 U-D 分解卡尔曼滤波

常规卡尔曼滤波存在数值稳定性较差,计算复杂等问题,针对这一点可引入U-D 分解改进.

常规卡尔曼滤波更新方程[8-9]:

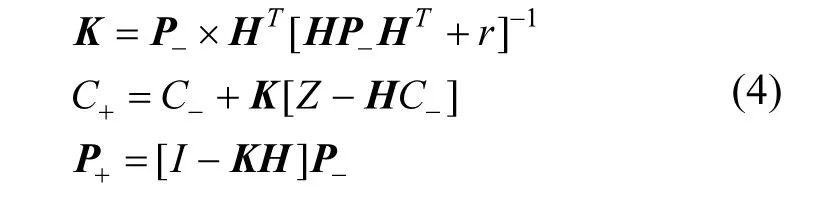
式中:K 为卡尔曼增益矩阵,P 为n 阶误差协方差矩阵,C 为n 维状态向量,表示浓度估计值;-、+号表示先验估计与后验估计;Z 为采样值,r 是采样误差的方差,H 是1×n 阶量测矩阵,采样点处矩阵元素为1,其余位置为0,H = [0…0,1,0 … 0];I 是n 阶单位向量.

P 矩阵更新时矩阵相减易导致矩阵稳定性降低,甚至引发滤波发散,将P 矩阵分解为P=UDUT的形式,方程表示如下:

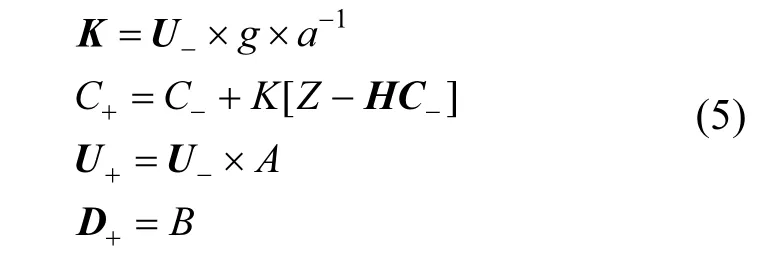
其中

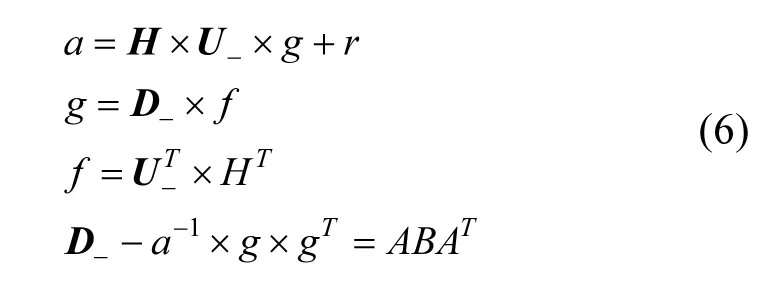
式中:U 为单位上三角矩阵;D 为正定对角矩阵.

1.4 权重更新

每个潜在污染源均值浓度场对应的污染羽为单个污染羽,综合浓度场对应的污染羽为综合污染羽.确定污染源的个数与位置需要通过污染源权重判断,将综合污染羽与单个污染羽标准化,用模糊集表示(所有浓度值除以最大浓度值),每个模糊集合的元素隶属度都大于等于给定的αi,本文取值为0.2、0.4、0.6、0.8.

将以模糊集形式表示的综合污染羽与各单个污染羽进行比较,记录二者的公共面积Si,计算出全局相似度并用各污染源全局相似度除以各污染源全局相似度中的最大者,即可算得各污染源的权重.全局相似度为[7-9]:

式中:g 为全局相似度;αi为模糊集标准值,i=1,2,…;Si为综合污染羽与单个污染羽在同一αi下的交叉面积.

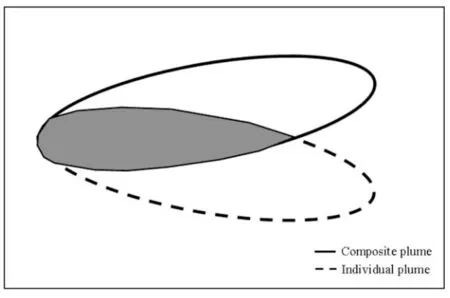
图2 污染羽对比示意Fig.2 Comparison of pollution plumes

1.5 优化模型建立

以污染物监测浓度与模拟计算浓度拟合误差极小化为目标函数,污染源释放强度为待求变量,替代模型作为优化模型等式约束条件,同时考虑源强上下限等约束条件,建立非线性规划优化模型

目标函数:

约束条件:

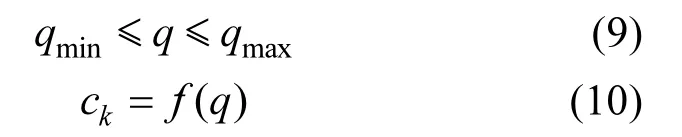
式中, q 为污染源释放强度,n 为采样点个数,ck为替代模型输出的模拟值,cˆk为实测值,f 为替代模型.

1.6 替代模型

应用遗传算法求解优化模型的过程中会大量调用溶质运移模拟模型,使用克里格方法建立溶质运移模拟模型的替代模型能有效减少运算负荷.替代模型回归方程为

2 假想算例

2.1 问题概述

图3 污染场地Fig.3 The plan of contaminated site

假定研究区大小为1000m×1000m,潜水含水层厚度为20m,介质为粗砂,含水层非均质各向同性.忽略非饱和带的影响.南北边界为已知水头边界,以含水层底板为基准面,北边界水位为16m,南边界水位为14m;东西边界为隔水边界.模型模拟时间长度为500d,分为5 个时段,每个时段为100d.研究区接受降雨入渗补给,5 个时段降水量分别为100,300, 100,50,100mm.忽略研究区蒸发蒸腾作用的影响.结合场地信息与专家经验,估计潜在污染源个数为4 个(图3),并给出潜在污染源的初始权重(权重表示潜在污染源为真实污染源的可能性大小,取值0～1 之间),Ⅰ、Ⅱ、Ⅲ、Ⅳ号污染源分别为0.6、0.7、0.7、0.6.设定Ⅲ号为真实污染源,污染源泄漏流量为2000mg/d.

2.2 问题分析

2.2.1 位置个数反演 将研究区剖分成20×20 的网格,应用GMS 软件的MODFLOW 和MT3DMS 模块建立溶质运移模拟模型,考虑场地信息的不确定性,对模型中的参数进行Morris 全局灵敏度分析,筛选出渗透系数K、纵向弥散系数Ld、给水度Sy、降雨入渗补给系数α灵敏度最高的参数作为随机变量.共有15 种组合方式,具体方法参照文献[21].

表1 参数组合方式Table 1 Combination-patterns of parameters

图4 参数灵敏度分析Fig.4 Sensitivity analysis of parameters

从图4 可以看出,渗透系数灵敏度最高,本研究将渗透系数作为随机变量,其余参数作为确定性变量,应用拉丁超立方抽样生成110 组渗透系数随机场并进行相关性排序,场地存在4 个潜在污染源,输入模型得到4×110 组溶质浓度场,计算得出初始综合浓度场和误差协方差矩阵,Ⅲ号污染源的均值浓度场作为真实浓度场.

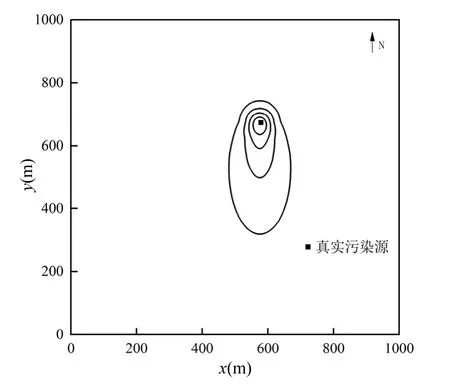
图5 真实污染羽Fig.5 True pollution plume

将采样点数据带入U-D 分解卡尔曼滤波更新方程对综合浓度场和污染源权重进行更新,图为浓度场和权重更新结果.

图5 为污染源真实污染羽,图6 为初始综合污染羽.从图7 可以看出,经过4 次采样更新后,综合污染羽逐渐收敛于Ⅲ号污染源,与真实污染羽相似.4 个污染源权重从0.6,0.7,0.7,0.6 变为0,0.2,1,0.05,可以判断出Ⅲ号污染源为真实污染源,更新完成后污染羽中浓度最高处就是污染源位置.

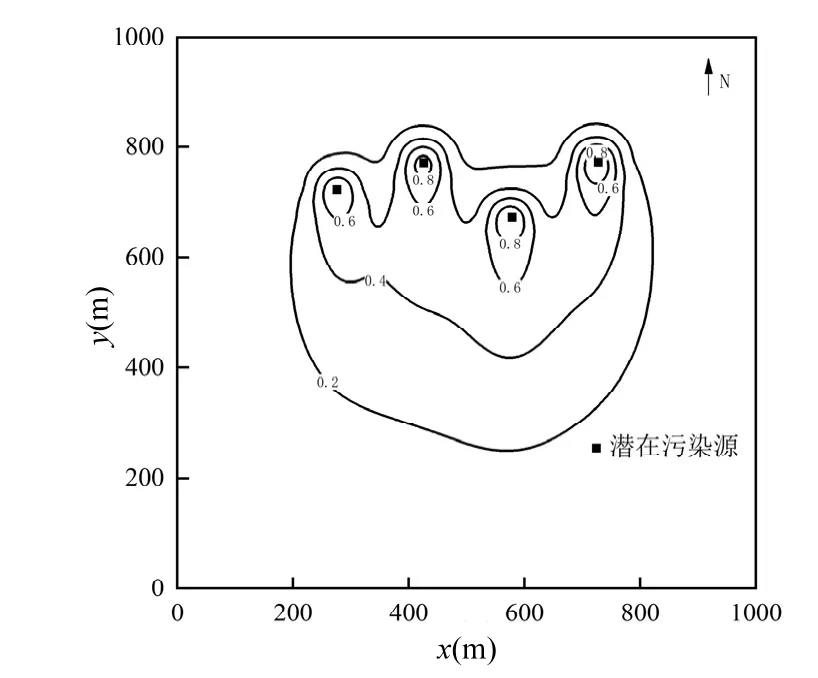
图6 初始综合污染羽Fig.6 Initial composite pollution plume

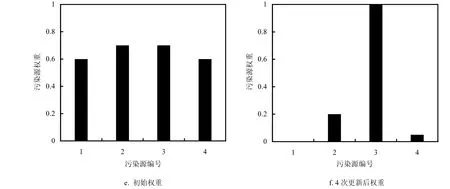
图7 污染羽与权重更新Fig.7 Update composite pollution plume and source location weight

2.2.2 源强反演 在运用U-D 分解卡尔曼滤波反演出污染源的个数和位置的基础上,建立优化模型并应用遗传算法求解.采用克里格插值法建立模拟模型的替代模型,应用拉丁超立方抽样获得80 组源强,输入模拟模型得到4 口采样井的输出,生成80 组输入-输出样本,前60 组作为训练样本,后20 组作为检验样本,将平均相对误差(MRE)作为克里格替代模型近似精度的评价指标,结果见表2.

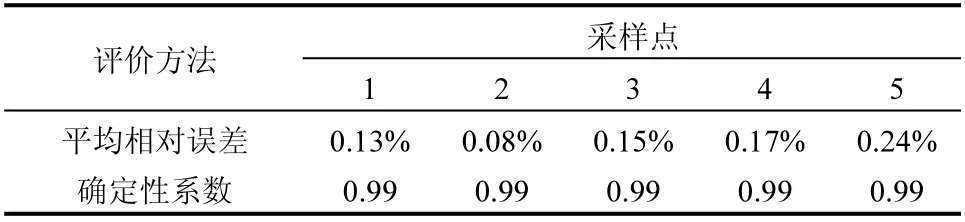
表2 替代模型精度评价Table 2 Accuracy assessment of surrogate model

由表2 可知,误差精度不超过1%,替代模型符合精度要求.

以污染物监测浓度与模拟计算浓度拟合误差极小化为目标函数,污染源释放强度为待求变量,替代模型作为优化模型等式约束条件,同时考虑源强上下限等约束条件,建立非线性规划优化模型.采用MATLAB 软件中的遗传算法工具箱求解优化模型,经过 46 次迭代求得源强 1972mg/d,与真实值2000mg/d 接近,相对误差1.4%,源强反演精度较高.

3 结论

3.1 将协方差矩阵进行U-D 分解,能够避免在迭代计算过程中卡尔曼滤波因为协方差矩阵可能出现不对称或者负定,导致迭代过程发散的情况,保证了卡尔曼滤波的数值稳定性,使迭代过程更容易收敛.算例表明基于U-D 分解的卡尔曼滤波,能够准确地辨识含水层中污染源的个数与位置.

3.2 采用局部灵敏度分析方法筛选出渗透系数K对模型输出影响最大,作为反映场地信息不确定性的随机变量输入模型建立浓度场库.

3.3 针对污染源释放强度辨识问题,建立非线性规划优化模型.应用遗传算法求解非线性规划优化模型,能快速计算出污染源释放强度.应用克里格方法建立地下水污染质数值模拟模型的替代模型,将克里格替代模型代替模拟模型嵌入优化模型,能够在保证精度的同时减少大量的运算负荷和运算时间.