Actor-Critic强化学习方法及其在开发基于计算机视觉的界面跟踪中的应用
2021-03-17OguzhanDogruKirubakaranVelswamy黄彪
Oguzhan Dogru , Kirubakaran Velswamy , 黄彪*
Department of Chemical and Materials Engineering, University of Alberta, Edmonton,AB T6G 1H9, Canada
1.引言
油砂矿石含有沥青、水和矿物质。沥青是一种高黏度的烃混合物,可以通过多种化学和物理过程进行提取。该产品在后处理装置或炼油厂[1]中进行进一步处理,以获得更有价值的副产品(如汽油、航空燃料)。油砂是从露天矿坑中开采出来的,再通过卡车被运送入破碎机[2]。此后,用热水处理混合物,并通过水力将混合物输送到萃取厂。曝气和几种化学品被引入这一过程以加强效果。在萃取厂中,混合物在初级分离容器(PSV)中沉淀。图1总结了水基油砂分离过程。
在PSV 内部的分离过程中,会形成三层:泡沫层、中矿层和尾矿层(图2)。在泡沫层和中矿层之间形成一个界面[以下称为泡沫-中矿层界面(FMI)]。其水平参照PSV单元影响萃取的质量。
为了控制FMI水平,关键是需要有可靠的传感器。传统上,差压(DP)单元、电容探头或核子密度剖面仪被用于监测FMI。然而,这些检测结果要么不准确,要么不可靠[3]。视镜被用于人工监视界面是否存在任何过程异常。为了在闭环控制中使用这一观察方法,参考文献[3]建议将相机用作传感器。该方案利用边缘检测模型和图像粒子滤波来获得FMI;然后使用该模型建立反馈控制。最近,参考文献[4]结合边缘检测和动态帧差分来检测界面。该方法直接使用边缘检测技术来检测界面,并且使用了估计测量质量的帧比较机制;此外,该方法还可以检测故障。参考文献[5]使用混合高斯分布对泡沫、界面和中间体的外观进行建模,并使用时空马尔可夫随机场来预测界面。尽管利用基于界面外观或行为的模型解决了一些难题,但这些技术未能解决在环境条件不确定情况下的敏感性问题,如遮挡和过度/非高斯噪声。
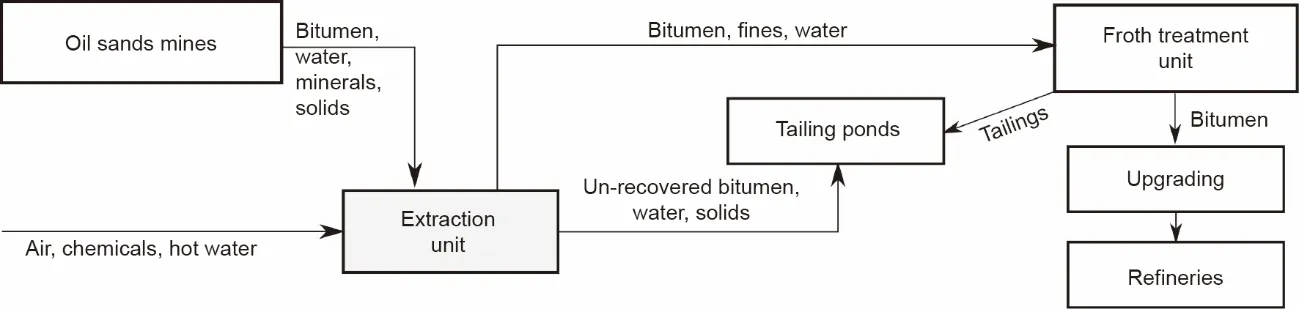
图1.水基油砂分离过程的简化图解。PSV位于提取单元中。
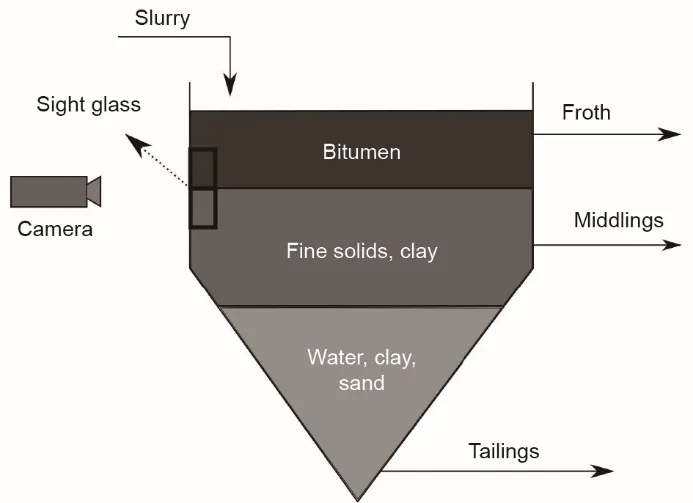
图2.PSV示意图。在分离过程中,形成三层分层。相机用于监控中矿层和泡沫层之间的界面,以控制FMI处于最佳水平。
监督学习(SL)方法尝试通过最小化代价(或损失)函数来构建从输入(即图像,x)到输出(即标签,y)数据的映射。通常,代价函数是凸函数,最优参数是通过对代价函数应用随机梯度下降算法[6‒7]来计算得到的。另外,无监督学习(UL)方法被用于查找未标记数据中的隐藏特征(即仅使用x)[8]。目标通常是压缩数据或在数据中找到相似之处。尽管如此,即使输入与输出之间确实存在着因果关系,UL 技术并未考虑输入对输出的影响。在计算机视觉中,这些方法是使用卷积神经网络(CNN)实现。CNN 是对输入应用卷积运算的参数函数。它不仅可以对一个像素进行处理,还可以对它的相邻像素进行处理来提取抽象特征,用于分类、回归、降维等[9‒12]。尽管CNN已经被使用了几十年[13‒16],但直到最近它才在不同领域得到广泛普及[17‒20],这是由于硬件技术[21]和数据可用性[22]的发展导致的。与计算机视觉的发展并行,循环神经网络(RNN)被用于预测时间序列,其中网络先前的输出以递归矩阵乘法的形式反馈到自身[23]。然而,vanilla RNN[24]会受到梯度减小或爆炸的影响,因为它反复将先前的信息反馈给自身,导致隐藏层之间反向传播数据的共享不均匀。因此,当数据序列任意长时,它往往会失败。为了克服这个问题,研究人员已经提出了更复杂的网络,如长短期记忆(LSTM)[25]和门控循环单元[26]。这些网络促进了隐藏层之间的数据传输,从而提高了学习效率。最近,研究人员提出了卷积LSTM(Conv‐LSTM)[27],它是LSTM的一种变体,可以通过用卷积运算替换矩阵乘法来提高LSTM 性能。与全连接LSTM 不同,ConvLSTM接收的是一个图像而不是一维数据;它利用输入数据中存在的空间连接提高估计的性能。具有多层的网络被认为是深层结构[28]。为了进一步提高预测准确度,研究人员已经提出了各种深度架构[29‒33]。然而,这些结构存在过度参数化的问题(即训练数据点的数量少于参数的数量)。研究人员试图从几种正则化技术(如dropout、L2)[17]和迁移学习[也称为微调(FT)]方法[34‒35]中找到解决方法,以提高网络的性能。然而,传输的信息(如网络参数)对于目标域可能不具有普适性。这一问题非常关键,特别是当训练数据不足,或它们的统计数据与目标域中的数据明显不同时。此外,目前循环网络的有效迁移学习问题仍然需要进一步研究。
强化学习(RL)[36]结合了SL和UL技术的优点,并将学习过程形式化为马尔可夫决策过程(MDP)。受动物心理学[37]和最优控制[38‒43]的启发,该学习方案涉及智能体(即控制器)。与SL或UL方法不同,RL不依赖于离线或批处理数据集,而是通过与环境交互生成自己的数据。它通过考虑直接后果来评估其操作的影响,并通过推导来预测其价值。因此,它更适用于涉及复杂系统决策的真实或连续过程。然而,在基于采样数据的方案中,训练阶段的数据分布可能会有显著差异,这可能会导致估计的方差较高[36]。为了结合价值估计和策略梯度的优点,研究人员提出了actor-critic方法[44‒46]。这种方法将智能体分为两部分:actor 决定采取哪个动作,而critic 使用动作值[47]或状态值[48]函数估计该动作的好坏。这些方法不依赖任何标签或系统模型。因此,对状态或动作空间的探索是影响智能体性能的重要因素。在系统辨识[49‒51]中,这被称为辨识问题。研究人员已开发出来多种方法来解决勘探问题[36,48,52‒58]。作为机器学习[59‒61]的一个子领域,RL被用于(但不限于)过程控制[2,42,61‒68]、游戏行业[69‒77]、机器人和自动驾驶汽车等领域[78‒81]。
FMI跟踪可以被表述为一个对象跟踪问题,它可以分别使用无检测或基于检测的跟踪方法通过一个或两个步骤来解决。先前的工作[82‒84]已将RL 用于对象检测或定位,因此它可以与跟踪算法相结合。在这种组合的情况下,跟踪算法也需要可靠和快速的实时实现。一些对象跟踪算法已被提出,包括使用RL[85‒90]的多个对象跟踪算法。研究人员所提出的方案将预训练的对象检测与基于RL 的跟踪或监督跟踪解决方案相结合。这些模拟是在理想条件下进行的[91‒92]。基于对象检测的方法的性能通常取决于检测准确度。即使智能体根据明确定义的奖励信号去学习跟踪,研究人员也应确保感官信息(或感官信息的特征)准确。基于模型的算法通常假设感兴趣的对象具有刚性或非刚性形状[4],并且噪声或运动方式具有特定模式[3]。当意外事件发生时,这些假设可能不成立。因此,无模型方法可能会提供更通用的解决方案。
由于CNN 可能会提取抽象特征,因此在训练后对其进行分析很重要。常见的分析技术利用激活函数、内核、中间层、显著性映射等信息[30,93‒95]。在RL情境中,一种流行的方法是使用t-分布随机邻居嵌入(t-SNE)[96]来降低观察到的特征的维度,以可视化处于不同状态的智能体[72,97‒98]。这有助于根据智能体遇到的不同情况,对行为进行聚类。另一种降维技术,即一致流形逼近与投影(UMAP)[99],将高维输入(在欧几里德空间中可能没有意义)投影到黎曼空间。这样可以降低非线性特征的维度。
图3展示了过程工业中的一般控制层次结构。在一个连续的过程中,层次结构中的每一层都以不同的采样频率相互交互。交互从设备层开始,这会对上层产生显著影响。最近,参考文献[2]提出了执行层面的解决方案。然而,解决其他层面的问题仍然具有挑战性。
本文提出了一种基于RL的新型界面跟踪方案,该方案针对无模型顺序决策智能体进行了训练。这项工作包括:
•详细回顾了actor-critic算法;
•聚焦设备层,以提高层次结构的整体性能;
•将界面跟踪表述为无模型的顺序决策过程;
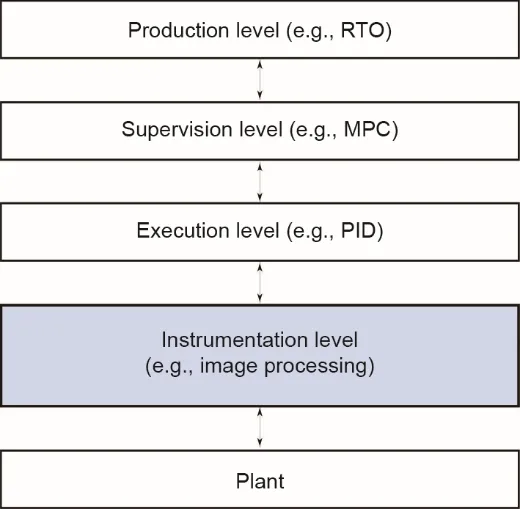
图3.过程工业中的一般控制层次结构。RTO:实时优化;MPC:模型预测控制;PID:比例积分微分控制器。
•结合CNN和LSTM以提取时空特征,无需任何显式模型或不切实际的假设;
•在奖励函数中利用DP 单元测量值,无需任何标签或人工干预;
•使用时间差学习训练智能体,允许智能体在闭环控制设置中持续学习;
•在开环设置的不确定性中验证鲁棒性;
•在简化的特征空间中分析智能体的可信度。
本文的结构如下:第2 节回顾了actor-critic 算法和基本信息;第3节阐述了界面检测;第4节详细介绍了训练和测试结果;第5 和第6 节分别给出了结论及未来研究展望。
2.Actor-critic强化学习研究综述
RL是一个严格的数学概念[36,39,42],其中的智能体学习是一种在动态环境中使整体回报最大化的行为。与人类类似,智能体学习通过考虑未来的奖励学习如何做出明智的决策。这与简单分类或回归等方法不同,它意味着观察的时间维度将被纳入考量。此外,这种能力允许强化学习在具有不规则采样率的条件[40]下得到应用。其通用性使得强化学习能够适应不同的环境条件,并能从模拟环境转移到实际的应用过程中[80]。
2.1.马尔可夫决策过程(MDP)
MDP 通过元组M形式化离散的顺序决策过程,M由〈X,U,R,P,γ〉组成,其中x∊X,u∊U,r∊R⊂R,分别表示状态、动作以及奖励。P(x′,r|x,u)表示确定或随机的系统动力学或状态转移概率。MDP 满足马尔可夫性质[100],即未来状态仅依赖于当前而非之前的状态。在该过程中,系统动力学对于智能体而言是未知的,这使得该方法更为通用。折扣因子γ∊[0,1)是未来奖励的权重,以使其总和有界。随机策略π(u|x)是从观察到的系统状态到动作的映射。
在MDP 中,智能体观察状态x0~σ0,其中σ0表示初始状态的分布。随后,它选择一个动作u~π(u|x),智能体被 带 入 下 一 个 状 态x'~P(x',r|x,u), 并 获 得 奖 励r~P(x',r|x,u)。通过利用序列(即x,u,r,xʹ),智能体学习了策略π,它将会产生最大折现收益G,如式(1)中所定义[36]:

式中,t和k表示离散时间步长。状态值vπ(x)和动作值qπ(x,u)使用贝尔曼(Bellman)方程[式(2)和式(3)]计算:

式中,E是随机变量的期望。在为每个状态估计值函数之后,可以使用式(4)和式(5)求解最优值(和)函数:
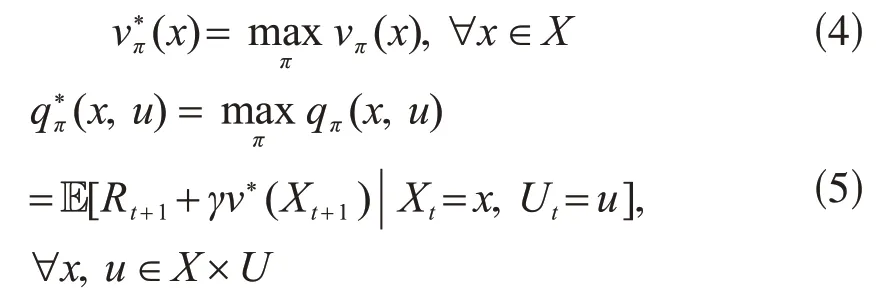
随后,最优策略π*可由下式求得:
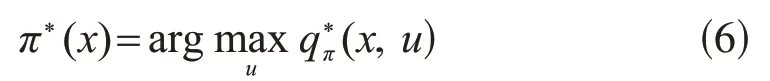
对于大规模问题,可以使用线性或非线性函数逼近法来分别或同时找到逼近值函数Q(x,u|ω),V(x|ω),其中,ω表示逼近函数的参数。该结构也被称为critics。此项工作侧重于状态值估计并将其符号简化为V(∙)。
2.2.Actor-critic算法综述
早期的方法使用基于值(仅critic)的RL[71,101]来解决控制问题。在这些方法中,动作直接来自值函数,据研究报道,该值函数对于大规模问题是发散的[45,102]。基于策略(仅actor)的方法[103‒105]解决了这个问题,它可以通过直接从参数化函数生成策略学习随机行为,然后使用性能指标直接优化此函数。然而,估计的方差和延长的学习时间使得策略梯度无法实现。类似于利用生成网络与判别网络的生成式对抗网络(GAN)[106],actor-critic算法无需任何标签即可进行自我监督[44‒45,107‒108]。这些技术分别通过actor和critic将策略与基于值的方法结合起来。这有助于大幅降低估计的方差和学习最优策略[36,55]。Actor 和critic 可以分别表示为两个神经网络;π(u|x,θ)(其中,θ表示actor 网络的参数)和V(x|ω)[或Q(x,u|ω)]。
虽然已有研究提出了一些基于模型的actor-critic方案[109‒110],但本文将重点介绍最常用的无模型算法,如表1所示。其中一些方法使用熵正则化,而另一些则利用启发式算法。上述方法中,一个常见的示例为ε-贪婪策略,其中智能体以概率ε∊[0,1)进行随机动作。其他研究技术包括但不限于向动作空间引入加性噪声、向参数空间引入噪声,以及利用置信上限等。感兴趣的读者可以参阅参考文献[67]了解更多细节。

表1 基于动作空间类型和探索方法的actor-critic算法的比较。对于所有算法而言,状态空间可离散或连续
将Actor-critic算法总结如下。
2.2.1.深度确定性策略梯度
已有研究提出,该算法可用于将离散的、基于低维值的方法[71]推广至连续动作空间。深度确定性策略梯度(DDPG)[47]采用actor和critic(Q)以及目标critic(Q′)网络,后者是critic 网络的副本。在观察到一个状态后,该方法将从actor 网络中采样实值动作,并与随机过程(如Ornstein-Uhlenbeck过程)[111]混合,以鼓励探索。智能体将状态、动作与奖励的样本存储在经验回放池中,以打破连续样本之间的相关性,从而优化学习。它使损失函数L的均方误差最小化,以优化critic,如式(7)所示。
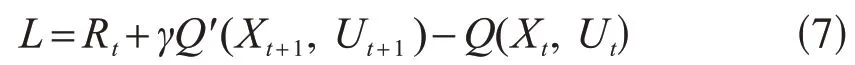
该方案利用策略梯度来改进actor 网络。由于值函数是经基于不同行为策略的目标策略所学习得到的,因此DDPG是一种新策略(off-policy)方法。
2.2.2.异步优势动作评价算法
异步优势动作评价算法(A2C/A3C)[48]没有将经验存储在需要内存的回放池中,而是让本地线程与环境交互并异步更新至公共网络,这从本质上增加了探索过程。
与最小化基于Q函数的误差不同,该方法会最小化critic 更新的优势函数(A或δ)的均方误差,如等式(8)所示。

在该方案中,公共网络通过式(9)更新,此外,策略的熵则被用于actor 损失函数中的正则化以增加探索,如式(10)所示:
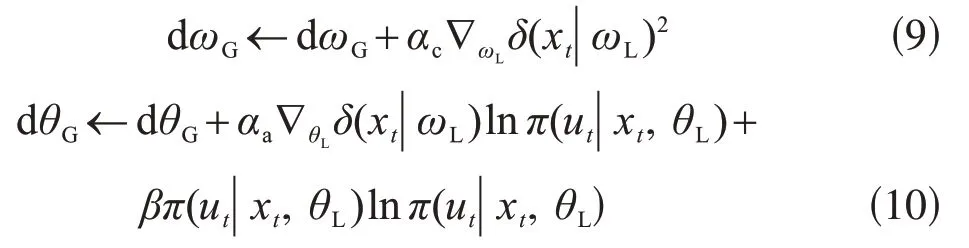
式中,初始dθG=dωG=0。左箭头(←)表示更新操作;αc和αa分别是critic 与actor 的学习率;∇是关于其下标的导数;β是一个固定的熵项,用于激励探索。下标L和G分别表示本地与公共网络。多线程网络(A3C)可以离线运算,且该方案可被简化为单线程(A2C)在线运行。尽管线程间相互独立,但他们会根据公共网络的行为策略来预测值函数,这使得A3C成为一种既定策略(on-policy)的方法。该项目使用A3C算法来跟踪界面。
2.2.3.有经验回放的actor-critic方法
具有经验回放的actor-critic(ACER)方法[112]利用Retrace 算法[113]解决了A3C 采样低效问题,该算法可估得式(11):

式 中 , 截 断 的 重 要 性 权 重ηˉt=min{c,ηt},ηt=[μ1(Ut|Xt)]/[μ2(Ut|Xt)],c是一个裁剪常数,μ1和μ2分别是目标和行为策略。此外,该方案利用随机竞争网络架构(stochastic dueling networks,以一致的方式估计V 和Q)和比先前方法更有效的信赖域策略优化(TRPO)方法[114]。由于其Retrace算法,ACER是一种新策略(offpolicy)方法。
2.2.4.近端策略优化
近端策略优化(PPO)方法[115]通过裁剪替代目标函数来改进TRPO[114],如式(12)所示:

式中,θ表示策略参数(即θold表示旧的策略参数);r(θ) =[πθ(u|x)]/[πθold(u|x)]和ε表示裁剪常数;A是表示智能体动作好处的优势估计,如式(8)所示。
2.2.5.Kronecker因子化置信区间的actor-critic算法
与使用梯度下降算法[6]来优化不同,使用Kronecker因子化置信区间的actor-critic算法是通过利用二阶优化来提供更多信息。它通过使用Kronecker 因子近似值来逼近费歇尔信息矩阵(FIM)的逆,以克服计算的复杂性,否则,该矩阵相对于近似的参数呈指数级缩放。此外,它还可以跟踪费歇尔统计,从而得到更好的曲率估计。
2.2.6.柔性actor-critic算法
与使用策略熵损失正则化的方法不同[48,114‒115,119],SAC(soft actor-critic,柔性actor-critic)算法[55,120]使用熵项[如式(13)所示]增加奖励函数以鼓励探索。相关研究[120]报道可以将这种方法用于提高策略对模型错误的鲁棒性。

式中,θ表示策略的参数;α代表用户自定义的(固定或时变)权重,用于调整熵的贡献;H=E[−lgπ(∙)]。该方案同时依赖于Q和V函数来利用柔性策略迭代。与DDPG和ACER类似,SAC将状态转移存储在回放池中以解决采样效率的问题。除了增强探索外,熵最大化还可以补偿由引入新策略方法而引起的稳定性损失。
2.2.7.双延迟深度确定性策略梯度算法
双延迟深度确定性策略梯度算法(TD3)[121]解决了由于函数逼近(approximation)和自展(bootstrapping)(即在更新过程中使用估计值,而不是精确值)而导致的错误传播(propagation)(这在统计和控制中是一项非常重要的挑战)[122]。为了实现这一目标,该算法会预测两个独立的动作值,并偏好悲观值;因此,它避免了次优策略。TD3利用目标网络,延迟策略函数的更新,并从回放池中采样N个状态转移来使用平均目标值估计,以减少学习过程中的方差。该算法向采样动作添加高斯噪声,以此引入探索,并使用确定性策略梯度方法执行策略更新[104]。
尽管上述算法提供了控制问题的一般解决方案,但它们可能仍然不能胜任某些更复杂或特定的任务。目前,研究者提出了许多其他的算法来弥补这些缺憾。例如,参考文献[123]通过哈密顿-雅可比-贝尔曼(HJB)方程[39,124],将参考文献[44]提出的离散的actor-critic 算法扩展到连续时间和空间问题中。随后,该算法在一个约束动作的钟摆问题和小车撑杆问题(cart-pole swing up)中得到了测试。参考文献[125]在有约束的MDP 上采用了actorcritic算法,并进行了详细的收敛性分析。参考文献[46]展示了四种基于正则和自然梯度估计的增量actor-critic 算法。参考文献[126]介绍了一种自然actor-critic算法(natu‐ral actor-critic,NAC),并展示了其在小车撑杆问题(cartpole)以及棒球挥杆任务中的表现。参考文献[127]通过反向HJB方程提出了一个连续时间actor-critic算法,并在两个非线性仿真环境中测试了其收敛性。参考文献[128]提出了一种适用于无限范围(infinite horizon)、连续时间问题和严格收敛性分析的在线actor-critic算法,并提供了线性与非线性模拟示例。参考文献[129]提出了一种增量的在线新策略actor-critic 算法。该算法定性地分析了收敛性,并用实证结果予以支持。此外,该研究还将时间差分算法(TD)与梯度-TD方法进行了比较,梯度-TD方法可以最大限度地减小预测的贝尔曼误差[36]。参考文献[130]提出了一种actor-critic标识符,理论表明,它可以在系统动力学未知的情况下逼近HJB方程。学习完成后,该方案会表现出过程稳定性。然而,该方案需要输入增益矩阵相关信息作为已知条件。参考文献[131]使用名义控制器作为监督者来指导actor,并在模拟巡航控制系统中实现更安全的控制。参考文献[132]提出了在保持稳定性的同时,在没有持续激励条件的情况下,学习部分未知输入约束系统的HJB方程的解。参考文献[133]考虑李雅普诺夫(Ly‐apunov)理论,设计了一种容错的actor-critic 算法,并在范德波尔系统(Van der Pol system)中对其稳定性进行了测试。参考文献[134]通过使用HJB 方程和二次成本函数来定义值函数,提出了一个输入有约束非线性跟踪问题。该方案可以通过actor-critic算法获得近似值函数。参考文献[135]结合分类和时间序列预测技术来解决最优控制问题,并在模拟连续釜式反应器(CSTR)和模拟非线性振荡器中演示了该方法。参考文献[136]提出了平均actorcritic(mean actor-critic)算法,该算法通过使用平滑Q函数来估计策略梯度,并用函数对动作求平均以减少方差;其结果在雅达利(Atari)游戏中得到了验证。参考文献[137]使用事件触发的actor-critic方案来控制供暖、通风和空调(HVAC)系统。除此之外,正如参考文献[2,62,67,138,145]中所述,研究者最近还对不同的actor-critic 算法及其应用进行了研究。
在强化学习(RL)中,已有研究提出了一些改进值估计的方法[146,148],这些方法均可用于actor-critic 算法。此外,还有研究提出了不同的技术[112,149],以提高采样效率(即减少学习最优策略所需的数据量)。与利用经验回放[70]或数据监督学习[150]的技术不同,并行学习(parallel learning)利用多个随机的初始化的线程(本地网络),这些线程独立地与环境的不同实例交互,以减少学习期间策略的差异。这些本地网络拥有与公共网络相同的基础设施,其所采集的k个样本将被用于公共网络的参数更新。由于各线程间的轨迹彼此独立,这将减少内存的使用并提高探索能力。任务分配可以通过多台机器[151]或一台计算机的多个中央处理器(CPU)线程执行[48]。
最优策略和最优评论在每个过程中都不同,并且它们往往是先验未知的。若使用蒙特卡罗类型的方法计算过程(或一个回合)结束时的经验回报[见式(1)],其结果往往会冗余且嘈杂。与心理学中的巴甫洛夫条件反射[152]类似,TD学习可以预测当前状态的值。与蒙特卡罗方法不同的是,它只在小范围下进行了低至一步的预测。这将无限范围问题转换为有限范围预测问题。与计算预期回报[如式(2)]不同,我们可以使用TD 误差δ的k步超前估计来更新critic 网络,如式(14)所示。这被称为策略评估。
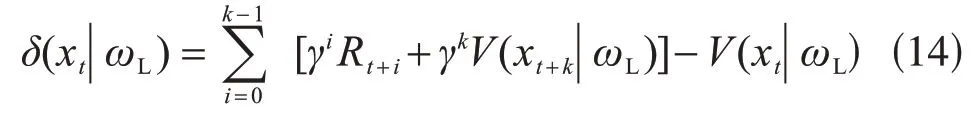
式中,δ是离散采样t瞬间状态x的TD 误差,给定本地网络的critic 参数ωL,k表示范围长度。如果k接近无穷大,求和项收敛于式(1)中给出的经验回报。与策略梯度算法[36]相比,基线V(xt|ωL)用于减少方差。
在k个步骤结束时,可以使用式(9)和式(10)更新公共网络的参数(即θG和ωG)。
3.将界面跟踪制定为一个顺序决策过程
3.1.界面跟踪
模型是描述过程动力学的数学方法,这些过程动态可以发生在物理/化学/生物系统[153]或视频[154]中。当出现意外事件(如遮挡)时,导出图像的模型通常会出现不准确的情况。为了克服这个问题,通常将上次有效观察的信息用于下一次观察[4],或重建图像[154]。尽管这些解决方案可能会在短时间内替代实际测量,但长时间暴露会降低闭环稳定性。因此,如果FMI太低,泡沫层中的沥青会流入尾矿。这会降低产品质量并产生环境足迹。相反,如果其水平更接近提取点,则被提取的泡沫中的固体颗粒会使下游操作复杂化[3]。由于FMI的偏差会影响下游过程,因此在最优点调节FMI非常重要。
RL 可以解决遮挡和过度噪声期间的不准确性。这可以通过将DP单元测量或来自任何其他可靠设备的测量与智能体的当前FMI预测相结合来完成,以在训练阶段提供奖励函数中所需的准确成本,而无需外部标签,如边界框。消除对此类标签的依赖可以最大限度地减少人为误差。为此,智能体可以在PSV 视镜上方的垂直轴上移动裁剪框,并将其中心与DP单元测量值进行比较。基于此偏差,智能体可以将框移动到最优位置,即框的中心与FMI的中心相匹配。这种偏差最小化反馈机制的灵感来自控制理论,它可以使用从实际过程中获得的测量值来增强基于图像的估计。
考虑从视频流中采样的灰度图像I∊RH×W,具有任意宽度W、高度H,它可以捕获整个PSV。考虑一个矩形裁剪框B∊RN×M,具有任意宽度M、高度N,其中,{N:N=-1,>1 ∊N},是矩形的中心。示例图像和裁剪框如图4(a)所示。这个矩形在将I裁剪成尺寸为N×M。为了完整起见,H>N,W=M。此外,将在时间t从DP 单元获得的界面测量值作为z。需要注意的是,DP单元仅用于RL 智能体的离线训练,并可以替换为其他界面测量传感器,这在离线实验室环境中是准确的。
这一问题的MDP组件可以定义如下:
状态:矩形内的像素,x∊B⊂X⊆I。这些像素可以被看做N×M个独立的传感器。
操作:将裁剪框的中心向上或向下移动1个像素,或冻结;u∊U={-1,0,1}。
奖励:在每个时间步长t,DP单元测量值与框中心位置(参考PSV底部)之间的差异见式(15)。

ut和之间的关系见式(16)。

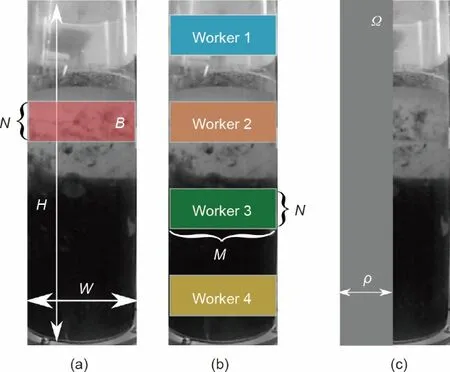
图4.使用相机获得的帧(I)。(a)图像尺寸(H×W)和裁剪框(N×W);(b)裁剪框的尺寸(N×M)和初始裁剪框位置;(c)一个比值为ρ的遮挡示例。
式中,是一个任意的初始点,求和项表示直到第t个时刻采取的动作(ui=+1表示向上,ui=−1表示向下)。
折扣因子:γ=0.99。
该智能体的目标是生成一系列操作,将裁剪框B覆盖在PSV的垂直轴上,界面位于其中心。为了实现这一点,智能体需要执行长期规划并保留其动作与从DP单元测量中获得的信息之间的关联。拟议方案的流程图如图5 所示。此外,图6 和表2 详细展示了网络。关于ConvLSTM层的更多细节,请参见参考文献[27]。
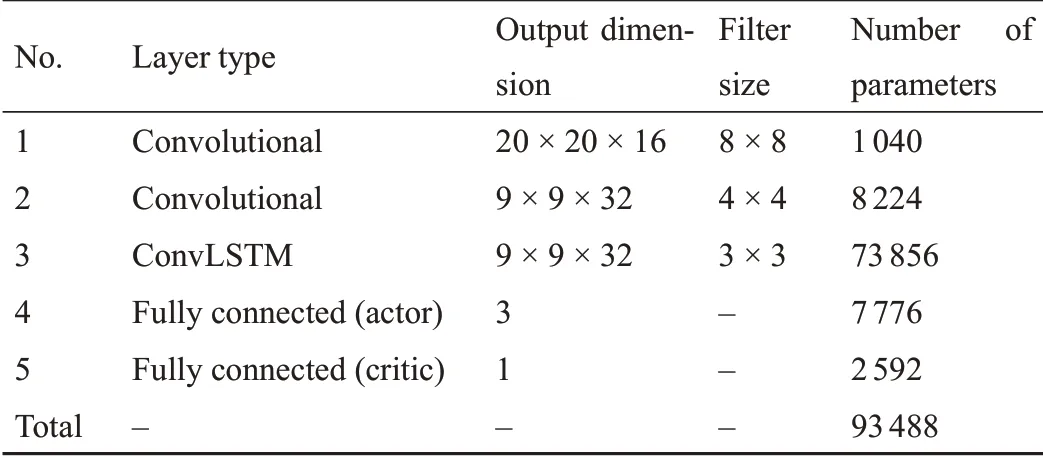
表2 全球网络的结构(与工作器的结构相同)
与之前在状态空间中进行预测的工作[4‒5]不同,这种方法通过分别使用式(9)、式(10)和式(14)来优化值和策略空间。此外,CNN 和ConvLSTM 层通过使用式(17)进行更新。
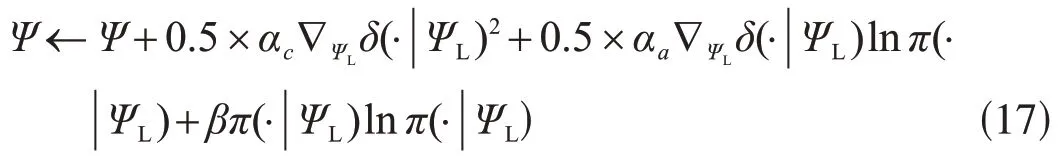
式中,Ψ=[ψCNN,ψConvLSTM]表示CNN 和ConvLSTM 层的参数。该方案仅使用TD 误差对整个网络进行端到端的训练。在不同点[图4(b)]初始化的多个工作器[48]可用于改进探索,从而提高泛化能力。
在找到次优策略后,智能体保证在有限的时间步k内找到界面,这与初始点无关,如引理3.1所示。

图5.本文提出的学习过程的流程图。更新机制如式(9)和式(10)所示,其k步策略评估如式(14)所示。

图6.CNN、ConvLSTM、actor和critic网络的详细结构。
引理3.1:在任何时刻t,对于一个常数zt,同时P=如k→N,对于(k≤N<|X|≪∞)^(∀z0,zt∊Z≡|X|)。
证明.假设并且次优参数θ*和ω*是使用连续策略函数π(∙|θ*)上的迭代随机梯度下降获得的。V(∙|ω*)是Lipschitz 连续critic 网络,由ω参数化,并估计给定状态的策略π(∙)的值。
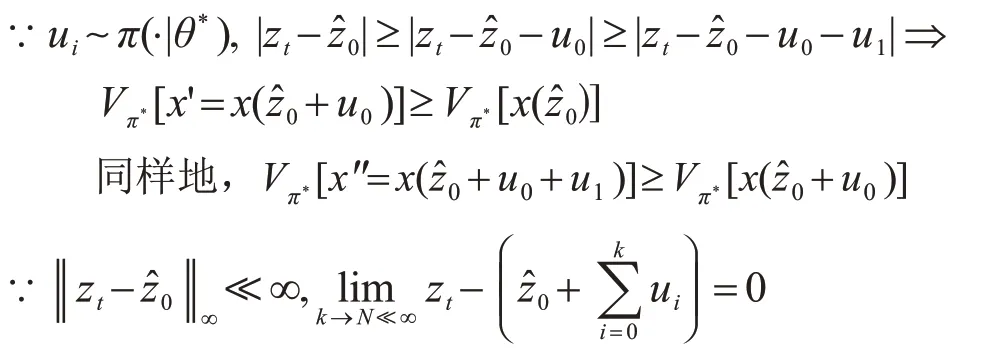
这可以被扩展到变量zt∊Z。
3.2.通过训练对遮挡的鲁棒性
CNN 通过考虑像素的连通性来解释空间信息,这在一定程度上提高了鲁棒性。但是,它并不能保证对遮挡的鲁棒性,即使在正常条件下获得了好的策略,智能体也可能会失败。为了克服这个问题,可以在训练阶段使用合成遮挡的图像来训练智能体。另一种方法是使用遮挡图像重新校准策略(使用无遮挡图像进行训练)。
具有任意像素强度κ∊[0,255]的遮挡物体Ω可以定义为{Ω:Ω∊RH×(N×ρ)},其中E[Ω]=κ。ρ∊[0,100%]表示遮挡的比率,如图4(c)所示。如果ρ=1,则智能体仅观察该视频帧中的遮挡(即,如果ρ=100%,则xt=Ω)。通过定义其尺寸后,可以从任意概率分布(即连续或离散,如高斯、均匀、泊松)中采样遮挡率。在训练过程中,可以任意调整出现遮挡的实例的持续时间。这些可以是随机或确定的。即,遮挡可以在随机(或特定)时间出现,并持续一段随机(或特定)时间。如果使用多个工作器(如第2.2节所述),则可能会在不同时间实例中为每个工作器引入不同的遮挡率。因为智能体不需要等待很长时间来观察不同类型的遮挡,所以这提高了训练数据的多样性,并且使得处理时间更加高效。
4.结果和讨论
4.1.实验装置
模拟工业PSV 的实验室规模设置用于提出的方案。这种设置允许使用泵将界面移动到所需的水平,如图7所示。两个DP单元用于根据液体密度测量界面水平,如参考文献[5]中所述。
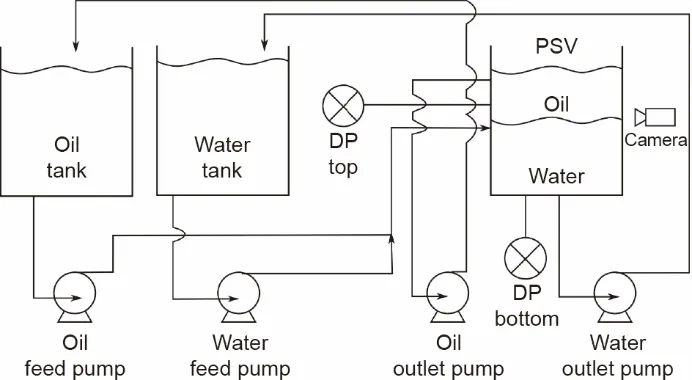
图7.实验装置。
使用D-Link DCS-8525LH相机以每秒15帧(FPS)的速度获取图像。从15FPS的镜头中,可以获得每秒的代表性图像。因此,通过必要的下采样获得了来自连续80 s的80 张图像。这些图像经过处理以展示PSV 部分,没有不必要的背景。然后将它们转换为灰度图像。DP 单元相对于进水处的FMI高度测量值(与图像相同的连续时间段)可以转换为像素位置,如参考文献[4]所示。执行每个动作后,视频帧会发生变化。智能体采取的每一个动作都会产生一个标量奖励[式(15)],之后用于计算训练智能体参数[式(9)和式(10)]时使用的TD误差[式(14)]。
4.2.实施细节
4.2.1.软件和网络详细信息
训练和测试阶段均使用Intel Core i7-7500U CPU,工作频率为2.90 GHz(两核四线程),8 GB 的RAM,工作频 率为2133 MHz,配 有Tensorflow 1.15.0 的64 位Win‐dows系统。与更深层次的网络(如参考文献[32]中包含数千万个参数的网络)不同,该智能体包含的参数较少,如表2 所示。这可以防止过度参数化,并显著减少计算时间,但其缺点是无法提取更高层次的特征[155]。
执行每个操作后,裁剪框的尺寸将调整为84像素×84像素。之后使用学习速率为0.0001的Adam优化器,以基于样本的方式对智能体的参数进行优化(包括CNN、CONVLSM、actor和critic)。相关研究显示这种基于动量的随机优化方法计算效率很高[156]。
4.2.2.无遮挡训练
实验中使用了A3C 算法以减少训练时间,提高探索度,并在学习过程中收敛到次优策略[48]。所有初始网络参数都是从均值和单位方差为零的高斯分布中随机抽样获得的。如图8所示,通过手动排序80幅图像创建界面级连续轨迹后,进行离线训练。
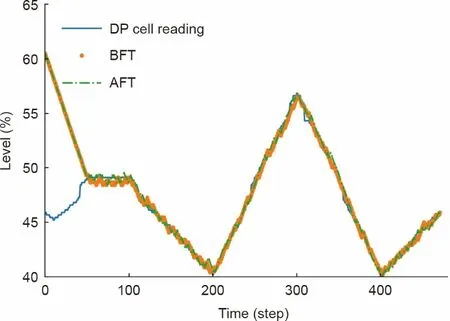
图8.训练结束时的训练结果(2650回合)和FT(3380回合)。BFT:微调前;AFT:微调后。
然后,在470 步,共2650 回合(episode,一回合包含470 步)中,向智能体重复显示这一轨迹。无论何时,智能体都只观察裁剪框内的像素。每个智能体的裁剪框在四个不同的位置初始化,如图4(b)所示。智能体的目标是在最大速度为每步1像素的情况下,使裁剪框中心相对于DP单元测量值的偏差最小化。该智能体在训练阶段没有被遮挡,能够为4 个线程处理20 帧⋅s−1图片(即计算执行时间)。
4.2.3.无遮挡微调
在没有遮挡的情况下,利用训练结束时获得的参数初始化全局网络参数。本地网络最初与全球网络共享相同的参数。所有训练超参数(如学习率、界面轨迹)保持不变。前一个训练阶段使用的图像被遮挡,其比率ρ从泊松分布中采样获得,如式(18)所示。分布情况Pois(x,λ)的计算如式(19)所示。

每回合开始时,式(18)限定ρ的范围处于0~80%(ρmax)之间。形状因子可任意定义为λ=1。在每一回合中,遮挡发生在第200步到接下来的200步之间,概率为1。微调(FT)的目的是确保智能体对遮挡具有鲁棒性。该智能体与四个线程接受了730回合任意的训练,直到情景累积奖励得到改善。
4.2.4.界面跟踪测试
对于一个1000 步的回合,使用一个不连续的轨迹测试该智能体,该轨迹包含以前未看到过的图像,这些图像通常没有噪声或充满高斯噪声,ν∊RH×W~N(0,1),如表3所示,测试以三种方式进行。这些图像也使用合成遮挡,其恒定强度被任意选择为图像的平均值(即κ=128),而遮挡率ρ在20%~80%之间线性变化。4.2.5.特征分析
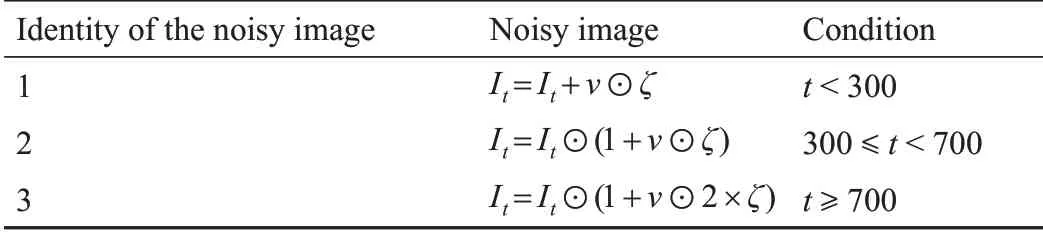
表3 基于图像身份的噪声图像定义
为了说明该网络的有效性,本实验从PSV 的顶部到底部手动裁剪了以前未看到的PSV 图像。这些手动裁剪的图像在训练前通过CNN逐一传递,CNN按照第4.2.2节所述的方式进行训练,同时按照第4.2.3 节所讨论的进行微调,以提取图像特征。然后将这些空间特征ϕs收集到一个尺寸为9 × 9 × 32 × 440 的缓冲区中,并使用UMAP[99]从中获得降维(2×440)特征。这些低维特征将在第4.6节中进行概述。
4.3.训练
最佳策略是在训练和FT 结束后获得的,此时连续500 回合的累积奖励没有得到改善。图8 显示了使用这些策略留下的轨迹。裁剪框的位置被初始化,其中心位于PSV 最大高度的60%处。在该阶段结束时,智能体跟踪界面的偏移量可以忽略不计。图9(a)中显示了从第80步获得的示例。绿色星形表示智能体认为界面在当前帧所处的位置。

图9.(a)第80帧的训练结果;(b)在第950步,80%遮挡和过度噪声的情况下进行AFT后的测试结果。白色框表示智能体控制的裁剪框,星形代表裁剪框的中心,圆形表示精确的界面水平,五边形是看似FMI的遮挡的底部。.
4.4.重新校准微调解决遮挡问题
如表4 所示,FT 将逐层的平均误差(MAE)降低了0.51%,提高了智能体的整体性能,包括无遮挡图像。这表明智能体不需要丢弃前置条件就能适应新的环境条件。这是因为从近优点出发,改进了智能体的估值能力和策略。需要注意的是,平均误差的最小值受裁剪框初始位置的限制,如图8所示。

表4 训练和FT结束阶段逐像素和逐层的平均误差
图10 以实线和点线分别表示了训练过程中和微调后(AFT)的累积奖励。
需要注意的是,FT期间的初始下降是由遮挡导致的,因为智能体在发生遮挡时无法跟踪到界面层。这个新特征是通过400 回合内闭环奖励机制学习得到。FT 结束时得到的最终累积奖励与训练结束时获得的基本相同。这是因为累积奖励仅表示训练阶段的跟踪性能,它取决于裁剪框的初始位置,如图8 所示。只有当框的中心和DP 单元测量在初始回合完全重叠,并且在此期间智能体无偏差地跟踪界面时,该值为零。如第4.5节所述,当智能体暴露在不可见的环境条件中时,例如,过度噪声和过度遮挡的情况,FT的必要性更为明显。
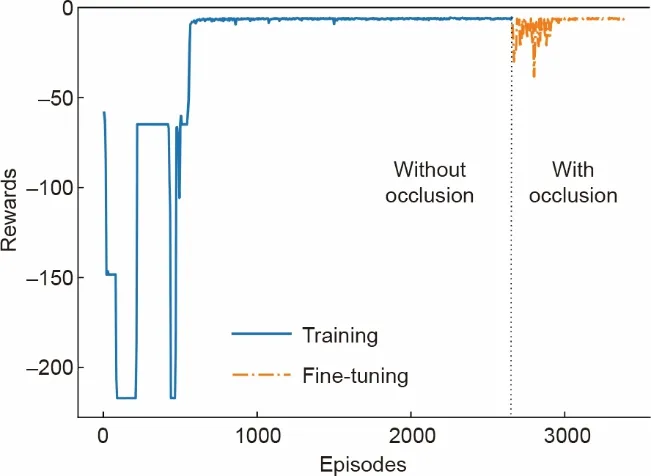
图10.累积奖励。图中显示了智能体可以学习遮盖理论并成功跟踪界面。
4.5.检测
4.5.1.微调前阶段
在初始训练结束阶段(即第2650 个回合,如图10 所示)进行初始前微调(BFT)测试。需要注意的是,测试阶段(在线应用)没用采用DP 单元信息,并且RL 智能体独立运行。事实上,即使DP单元可以使用,它在现场应用环境下也无法准确运用。图11 显示,微调前,智能体对50%的遮挡和附加噪声具有鲁棒性。这极大改进了现有方案未能解决的遮挡问题。改进方案的原理是,卷积消除了干扰并提高了智能体的整体性能,神经网络在空间域和时间域中提取了比边缘和直方图信息更多的抽象特征[157]。另外,任何增加遮挡率的操作行为都会导致跟踪界面失败。由于遮挡的强度较轻,策略会倾向于移向PSV的底部(此处存在大量较高强度的像素)以寻找界面。

图11.展示了检测结果,ρ 代表遮挡率(例如,ρ=0.8 表示图像被遮盖了80%)。
4.5.2.微调后阶段
在AFT 阶段中,重新校准作用于遮挡问题的智能体后,其性能得到显著提高,如图11 所示,智能体跟踪界面的准确率有所提高。当连续帧之间的界面偏移量约为5%时,附加的噪声会降低智能体的性能。然而,当界面偏移量减少到2.5%时,智能体可以成功运行,如图11所示。这是因为过多的噪声会严重破坏图像,导致智能体无法定位界面。在第950 帧处获得的示例帧如图9(b)所示。需要注意的是,80%的遮挡率附带着噪声,这给跟踪带来了挑战。智能体从图像中提取的有用信息量显著减少,此时图像中只剩下20%的像素可用于定位界面。这种性能归功于CNN 和ConvLSTM 的组合。如图12 所示,从随机网络(实线)、训练后(虚线)和AFT(点)获得的参数显示了智能体对从不可见画面中获得的状态的值(critic 预测)。根据式(2),这个图像定义了一个状态的值,它假设策略会生成到达界面层的最佳轨迹。
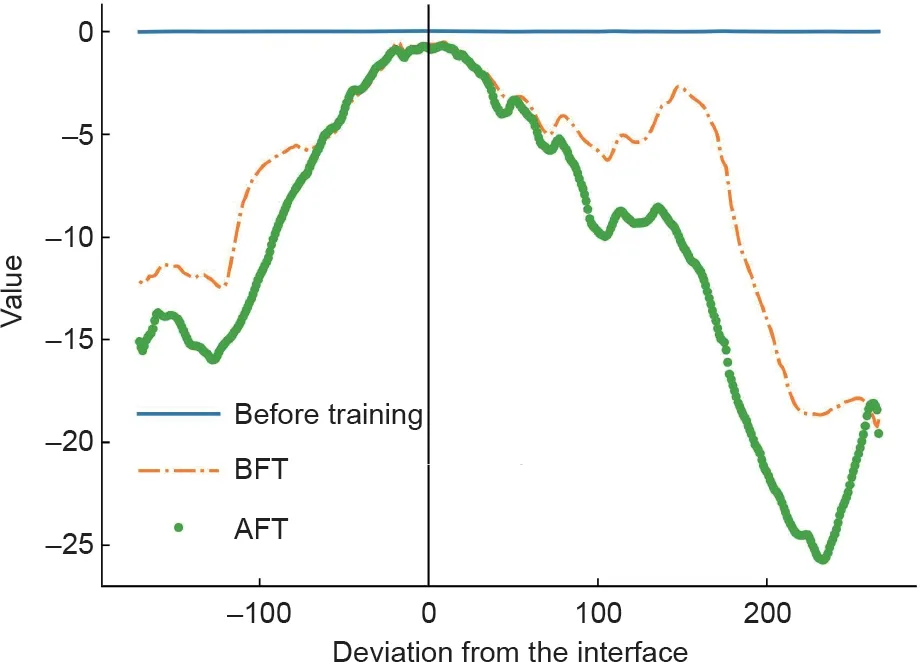
图12.值函数的测试结果与界面偏差的关系图。
图12 显示,在训练开始之前,任何状态的预测值都是相似的。但是,在训练阶段,智能体不安于处于劣势状态中,并且DP单元读数强调将裁剪框向界面移近(即垂直实线)得到的值比远离界面得到的值更优。在FT 结束阶段,随着数据的增加,智能体进一步改进自身的参数和行为,移动裁剪框,因此提高了准确度。结果表明,智能体尝试通过不断变化的值来改进其行为。需要注意的是,在偏差值为200后,AFT阶段的增加对应于图9中的黄色五边形。黄色五边形的外形与界面相似,并增大了值函数,但是从这个部分获取的值比界面的值低,这表明智能体靠近星星时比靠近五边形时更可信。
4.6.理解网络:特征分析
训练和测试结果集中于智能体学习和控制能力的进步。单凭这些可能不足以解释在以图像形式观察到的情况下,智能体的决定是否有意义。
图13 显示了二维图的降维结果,颜色的渐变强度表示对应裁剪图像(在第4.2.5 节中获得)的值。曲线(从左到右)对应于PSV 箱侧玻璃从上到下的裁剪图像,如第4.2.5节所述。
图13(a)~(c)中的有色五边形对应图13(d)中的三个点。结果表明,训练前从网络中得到的特征在没有特殊安排的情况下是相似的。然而,随着训练的推进,具有相似值的特征越来越接近。结合图12、图13可以推断,在RL 方法的帮助下,CNN 在未标记数据的无模型环境中,也能以有意义的方式提取特征,因为在采用CNNConvLSTM组合模型时,每个裁剪图像的纹理和像素强度模式可以成功转换为值和策略函数。此外,从DP单元获得的奖励信号(用作反馈机制)训练了智能体的行为。
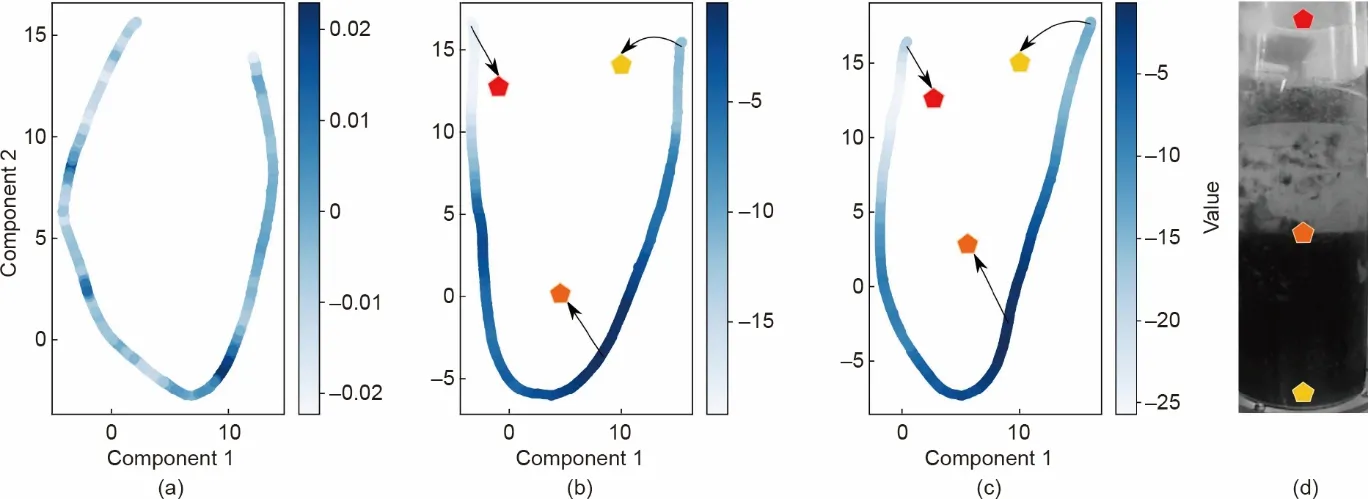
图13.降维方法被应用于从不可见图像中获得的状态特征中。这些特征的来源于随机(a)、训练(b)和微调(c)网络获得的参数。根据相应的值对数据点着色。(d)三个区域对应于箱体顶部和底部,并在不可见的图像上突出标记FMI。智能体训练过程中,从相似区域提取的特征在黎曼空间中聚集得更为紧密。
5.结论
本文全面回顾了actor-critic算法,并提出了一种新颖的RL方案。该方案把控制层次的设备层作为目标,提高了整个结构的性能。为此,本文把界面跟踪制定为一个需要长期规划的顺序决策过程。智能体由CNN和ConvLSTM共同组合而成,不需要任何形状或运动模型,因此对过程中的不确定性更具鲁棒性。受控制理论中使用的反馈机制的启发,智能体采用DP单元的读数来改进其行为。该方法不再依赖于SL 方案所需的显式标签。在使用遮挡和噪声下未经训练的图像进行验证时,智能体的性能表明,它可以在低于80%的遮挡和过度噪声的情况下实现对界面的跟踪。本文通过对高维特征的分析,验证了智能体对其观测值的概括能力。
6.未来研究
本文成功采用一种最先进的RL技术演示了跟踪液体界面的过程。本文利用由深度CNN 结构组成的智能体处理遮挡问题,并采用FT 策略提高了容限,这展示了该技术的自适应性。此外,本文认为能够重建遮挡图像的智能体可能是未来可行的替代方法。
Acknowledgements
The authors thank Dr.Fadi Ibrahim for his help in the laboratory to initiate this research and Dr.Artin Afacan for the lab-scale PSV setup.The authors also acknowledge the Natural Sciences Engineering Research Council of Canada(NSERC), and its Industrial Research Chair (IRC) Program for financial support.
Compliance with ethics guidelines
Oguzhan Dogru, Kirubakaran Velswamy, and Biao Huang declare that they have no conflict of interest or fi‐nancial conflicts to disclose.
Nomenclature
Abbreviations
A2C advantage actor-critic
A3C asynchronous advantage actor-critic
ACER actor-critic with experience replay
ACKTR actor-critic using Kronecker-factored trust re gion
AFT after fine-tuning
BFT before fine-tuning
CNN convolutional neural network
ConvLSTM convolutional long short-term memory
CSTR continuous stirred-tank reactor
DDPG deep deterministic policy gradient
DP differential pressure
FIM Fisher information matrix
FMI froth-middlings interface
FPS frames per second
FT fine-tuning
GAN generative adversarial network
HJB Hamiltonian-Jacobi-Bellman
HVAC heating,ventilation,air conditioning
LSTM long short-term memory
MAE mean average error
MDP Markov decision process
NAC natural actor-critic
PPO proximal policy optimization
PSV primary separation vessel
RL reinforcement learning
RNN recurrent neural network
SAC soft actor-critic
SL supervised learning
TD temporal difference
TD3 twindelayeddeepdeterministicpolicygradient
TRPO trust region policy optimization
t-SNEt-distributed stochastic neighbor embedding
UL unsupervised learning
UMAP uniformmanifoldapproximationandprojection
Symbols
E[ ⋅ ]expectation
ϕs(⋅) spatial features
ϕt(⋅) temporal features
δtemporal difference error
σ0distribution of initial states
νgaussian noise with zero mean unit variance
(⋅)*optimum value for the variable,e.g.,q*
ln(⋅) natural logarithm
R,Gempirical reward,return
q,r,vexpected action-value,reward,state-value
x,x'∈XStates ∈State space
u∈UActions ∈Action space
π(⋅) policy of the agent,also known as the actor
δ(xt|ωL)temporal difference error
V(⋅) estimate of state-value,also known as the critic
Q(⋅) estimate of action-value,also known as the critic
Ω occlusion
Parameters
αa,αclearning rates for the actor and critic:0.0001
γdiscount factor:0.99
κintensity of occlusion:128/256
λshape parameter of a Poisson distribution:1
ρocclusion ratio:%
ζmagnitude of noise:0.2
