基于锚杆受力分析的前支点挂篮中间索力确定方法
2021-03-17陈兆辉周水兴沈开孙测世
陈兆辉,周水兴,沈开,孙测世
(重庆交通大学 土木工程学院,重庆市 400074)
1 引言
斜拉桥的国际化研究始于20世纪70年代,于20世纪90年代得到迅速发展。其中自锚式混凝土斜拉桥常采用悬臂浇筑或拼装的施工方式,区别于连续刚构桥的悬臂浇筑,斜拉桥由于斜拉索的存在广泛采用前支点挂篮,受力与变形也更为复杂。前支点挂篮以斜拉索作为前支点,充分利用了当前节段斜拉索的弹性支撑作用,使挂篮和已浇筑节段的受力状态得到改善,提高了节段浇筑长度和挂篮承载能力,加快了施工进度。但随着悬浇主梁节段长度和重量的增加,往往需采用分次浇筑的施工方式,斜拉索也需进行分次张拉,施工工序较为复杂。如普遍采用的主梁分2次浇筑、拉索分3次张拉施工工序,确定施工过程中的拉索力是最重要的环节。
目前,关于前支点挂篮中间张拉索力的研究已有许多:李传习以挂篮中后挂点的最大张力和反顶力为控制条件确定中间索力可行域;颜东煌、李学文等以各工况中后挂点反力不超过挂篮空载状态下反力为控制目标,由静力平衡确定中间索力可行域;刘金秋分别按中后锚杆、主纵梁受力满足要求求解中间索力可行域,通过对比两个可行域得出满足锚杆受力要求的中间索力也满足主纵梁受力要求的结论;姜竹生通过对施工过程的模拟和挂篮受力分析确定中间索力可行域,并结合五河口斜拉桥施工控制验证了该方法的合理性;张玉平基于静力平衡条件建立静力平衡方程,确定了带顶升机构前支点挂篮中间索力可行域;张国栋将前支点挂篮简化为简支梁,由静力分析计算中间索力。
鉴于以上都是通过挂点反力确定中间索力可行域,计算时都未考虑锚杆预张力,且未详尽讨论中间一次张拉索力可行域。由于实际施工中,挂篮定位完成后需进行锚杆预张,此时数值较大的预张力将使后续施工阶段锚杆受力变得复杂。挂点支反力与预张力的大小将决定锚杆力的取值,若不结合两者分析锚杆受力,将与实际不符。此外,若能先通过计算确定合理的中间张拉次数,对于施工更有指导意义。
该文通过讨论中后挂点支反力与锚杆力的关系,以不同施工阶段挂点支反力不超过锚杆预张力为控制目标确定一张力、二张力可行域,在此基础上提出通过计算中间一次张拉索力可行域,判断能否减少张拉次数,结合有限元分析,在主梁受力满足要求的情况下最终确定中间索力。
2 前支点挂篮构造及施工流程
前支点挂篮一般由主桁、模板系统、吊挂系统、牵索系统、走行系统以及操作平台等组成,如图1所示。
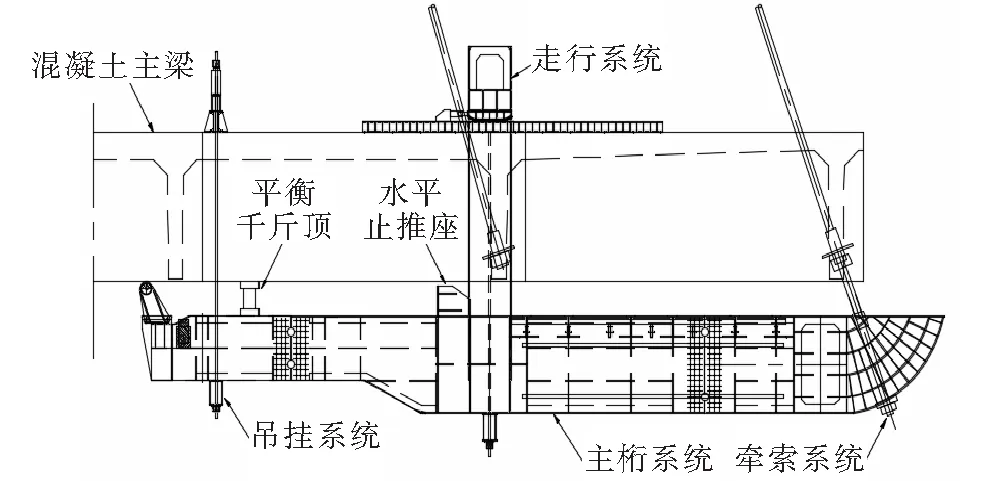
图1 前支点挂篮构造图
主桁结构中包含了主横梁、普通横梁、主次纵梁等构件,是整个挂篮施工过程中待浇节段的直接承载平台。模板系统处在主桁结构之上,由内模平台、平台滑道、内模升降系统、内模模板、端模模板、侧底模模板等构件组成。吊挂系统由中吊挂、后吊挂以及分配梁等构件组成,其作用是将主梁和挂篮的中、后吊点连接固定。牵索系统主要由张拉分配梁、牵索接长装置、张拉千斤顶等构件组成,其作用是在施工时连接斜拉索与挂篮的前支点,浇筑完成后将斜拉索下端锚点由挂篮前支点转换至主梁新浇节段上,形成体系转换。走行系统的作用是,每个悬浇施工阶段完成后将挂篮移动至下一个施工阶段的位置,主要由滑道、水平止推座、限位块及顶推千斤顶组成。操作平台是施工人员进行挂篮施工过程中的主要平台,一般设置在前支点挂篮的两侧以及下方,四周设有安全护栏以保证施工人员的安全。
混凝土斜拉桥主梁常采用斜拉索3次张拉、主梁2次浇筑的施工工艺,其主梁循环施工流程见图2。
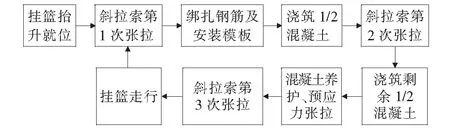
图2 主梁浇筑循环施工流程图
3 前支点挂篮施工过程受力分析
3.1 前支点挂篮受力分析
前支点挂篮的受力简图如图3所示。
图3中:R1、R2分别为已浇筑节段对挂篮后挂点A、中挂点B的支反力;H和T分别为水平止推座支反力和斜拉索索力;G和W分别为挂篮自重、待浇梁段混凝土自重。

图3 前支点挂篮受力简图
由静力平衡得到:
T·cosα=H
(1)
T·sinα-G-W=R1-R2
(2)
T·sinα·LT-G·LG-W·LW=H·h-R1·LR
(3)
将式(1)代入式(3)得:
(4)
将式(4)代入式(2)得:
(5)
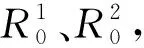
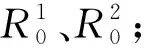
因此可由各个施工工况下求解的R1、R2,判断分析挂篮锚杆的受力情况。
(1) 斜拉索一张工况
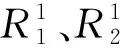
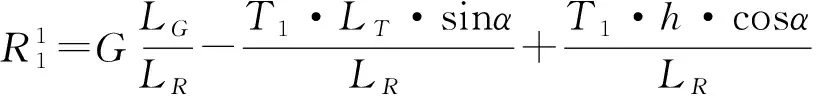
(2) 浇筑一半混凝土工况
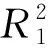
(3) 斜拉索二张工况

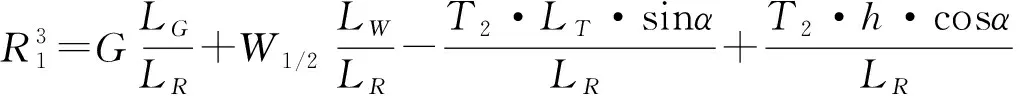
(4) 浇筑剩余一半混凝土工况
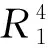
3.2 基于锚杆力控制的斜拉桥中间索力确定
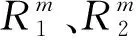

表1 挂篮锚杆受力随索力变化
斜拉索一张工况下中锚杆力、浇一半混凝土工况后锚杆力、二张工况下中锚杆力及浇筑完成工况下后锚杆力可以确定,而其余4个锚杆力分别与一张力、二张力的取值有关,需进一步讨论。
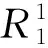
因此提出以不同施工阶段中后锚点支反力不超过锚杆预张力为控制目标,确定中间索力可行域。
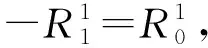
(6)
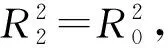
(7)
当计算出的T1min<0时,取值为0。
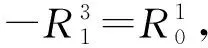
由于二张力还需满足浇筑剩余一半混凝土后索力不得超过三张力的条件,故:
T2max=min{T′2max,T3-ΔT2}
(8)

(9)
根据式(6)~(9)计算出一张力、二张力可行域上下限之后,可在可行域范围内对一张力、二张力进行取值。
3.3 求解中间一次张拉索力可行域
实际计算中,由式(6)~(9)得出的一张力、二张力可行域,可能存在交集或者较为接近。因此若能在一张力可行域集合中选取合适的子集,可实现中间一次张拉,无需二张,即斜拉索两次张拉、主梁一次性连续浇筑混凝土的施工流程。
中间一次张拉索力需满足3个条件:① 该可行域为一张力可行域的子集;② 浇筑完混凝土后,索力不能超过三张力;③ 浇筑一半混凝土时索力不能小于二张力下限值。
由此确定中间一次张拉索力T可行域:
Tmax=min{T1max,T3-ΔT1-ΔT2}
(10)
Tmin=T2min-ΔT1
(11)
在斜拉索中间索力满足挂篮受力要求的基础上,还需使主梁受力满足要求。实际施工计算时,可先按中间两次张拉计算一张、二张力可行域,再判断中间一次张拉索力可行域是否存在,若存在则取可行域内的值代入有限元模型中进行验证,根据施工过程中主梁的受力情况最终确定斜拉索中间索力。
4 工程实例
贵州沿河乌江三桥为“飞鸽式”异形塔双索面斜拉桥,主跨为160 m、边跨为145 m,采用塔、墩、梁固结体系,主梁为板式边主梁截面、C55混凝土结构,共20个浇筑节段。标准节段长7.3 m,截面面积为17.734 m2,横隔板体积为18.265 m3;非标准节段长5.5 m,截面面积分别为25.443、28.069 m2,横隔板体积分别为15.619、14.808 m3。
沿河乌江三桥采用前支点挂篮进行悬臂浇筑,主梁节段施工采用混凝土分2次浇筑、拉索分3次张拉的施工工序,施工步骤为:① 预拉中后吊挂,安装空挂篮;② 索导管安装定位,横梁、主梁底模及外侧模安装;③ 横梁、主梁钢筋绑扎,预应力管道安装,横梁、主梁内模及桥面底模安装,桥面钢筋绑扎;④ 第1次张拉斜拉索;⑤ 浇筑一半主梁混凝土及横隔板;⑥ 第2次张拉斜拉索;⑦ 浇筑剩余一半主梁混凝土;⑧ 待混凝土达到强度后张拉预应力,体系转换后第3次张拉斜拉索。
其标准节段挂篮结构尺寸如图4所示,桥型布置及Midas/Civil有限元模型如图5所示。

图4 标准节段挂篮结构尺寸图(单位:mm)
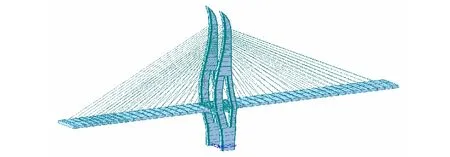
图5 桥型布置及有限元模型


表2 斜拉索中间索力计算结果 kN
由表2可知:取30%的安全储备后中间一次张拉索力可行域存在,先取其上下限平均值代入有限元模型中,计算表明各施工阶段主梁受力满足要求。在此基础上,还可根据主梁的受力情况对取值进行调整使主梁受力更为合理。
由此可知,由式(10)、(11)确定斜拉索中间一次张拉索力的方法合理可行,该桥施工虽已采用中间二次张拉斜拉索的施工工序,但其实也可减少中间张拉次数,加快施工进度的同时更方便进行施工控制。
5 结论
(1) 通过对前支点挂篮的静力分析,由索力T和待浇梁段重量W不同的取值,推导出各施工工况挂篮中后挂点的反力表达式,根据挂点反力与预张力的大小,分别讨论了中后锚杆3种受力情况,并据此分析各施工阶段锚杆受力。
(2) 整合斜拉索中间索力变化与挂点反力、锚杆受力的关系,提出了以不同工况下中后挂点支反力不超过锚杆预张力为控制目标确定中间索力可行域的方法,推导了中间索力可行域上下限的计算公式。在此基础上,提出通过计算中间一次张拉索力可行域来判断能否减少张拉次数、简化施工工序。
(3) 结合贵州沿河乌江三桥的实桥分析,为保证预拉杆不脱空按一定安全储备缩小预张力数值代入求解一张力、二张力可行域,以及中间一次张拉索力可行域。结果表明:中间一次张拉索力可行域不为空集,取上下限平均值代入有限元模型中进行分析,验证了该索力也满足主梁受力要求,同时表明该桥也可采用拉索两次张拉主梁一次性连续浇筑的施工工艺。
