基于电磁耦合的电网定向电压励磁自适应调控

张鑫，李甲骏，李世昌，王江淮，雷文焕

(1.河北张河湾蓄能发电有限责任公司， 河北 石家庄 050022；2.北京四方继保自动化股份有限公司， 北京 100084)

0 引言

大型的水电机组的励磁控制能够维持发电极端的电压，保证同步发电机的稳定运行，这是电网经济运行的基本条件。随着我国用电量的增大，发电机单机的容量和电网规模也在随之扩大，因此电力系统的安全稳定面临着严峻的考验[1-2]。水电机组中的励磁系统能够在系统故障状态时，迅速强力将励磁电压迅速上升至顶值电压，在强力时励磁机最大稳定电压与发电机额定转子电压的比大概在1.8-2之间，如果涉及远距离空间的情况下，这个数值可以提高到3-4[3]。在传统的励磁调控方法中，一般使用PID模糊调控，在发电机组单机容量比较大的时候，会由于一些不确定的因素，使得系统的参数不准确，导致电压上升的时间比较慢，影响电网供电结果[4-5]。提高励磁的控制功能是维持电力系统的稳定最经济有效的手段，因此本文研究有一定的实用价值。

1 基于电磁耦合的电网定向电压励磁自适应调控方法研究

1.1 建立水电机组励磁数学模型

水电机组中的定向电压励磁调控主要通过控制励磁电压来调节发电机端电压[6]，经过简化后的励磁系统结构,如图1所示。

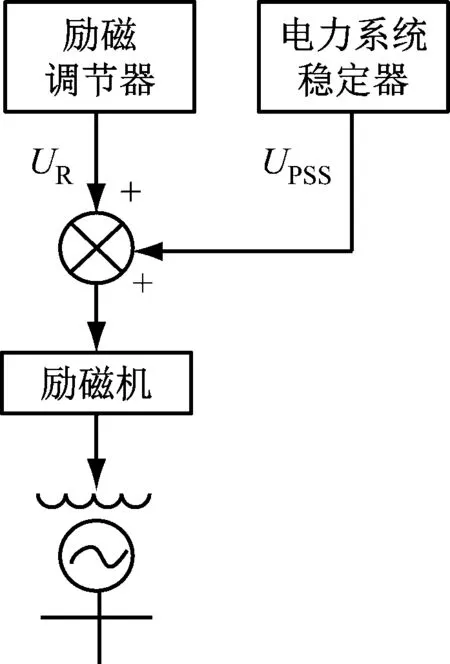
图1 发电机励磁系统结构

同步发电机励磁系统不仅要维持电压稳定，还需要对机组的无功发送进行调节[7-8]。励磁系统主要包括直流励磁和交流励磁两种形式，结构主要包括励磁调节器(AVR)和电力系统稳定器等，发电机励磁系统接收到调节系统的控制信号，并提供励磁电流给发电机转子，在这过程中的传递函数,如式(1)。

(1)

式中,Ef表示励磁机传送给发电机的励磁电压;UR表示励磁调节器的输出电压;KE表示自励系数，当励磁状态为他励时，KE的值为1;SE表示饱和系数，饱和程度越高，系数越大；TE表示励磁机的时间常数;AVR负责接收电压测量信号，并将误差信号转换为控制信号，对比较电路的测量,如式(2)。

UC=|UT+(Rc+jxc)IT|

(2)

整流滤波电路的测量,如式(3)。

(3)

式中,UC表示调差后的输出电压;UT表示发电机端电压;IT表示定子电流;Rc表示调差电阻;xc表示调差电抗;KR表示电压比例系数;TR表示测量时间常数。在实际的励磁模型中，还包括补偿电路(PSS)[9-10]，能够补偿相位偏差，PSS的传递函数,如式(4)。

(4)

式中,KPSS表示电路中的增益系数;Tsr表示测量时间常数;TW表示隔直环节时间常数。在传递过程中，一般情况下会有1-4个超前滞后的环境相连，因此具有不同的时间常数。将上述模型进行组合，便能得到励磁系统数学模型。励磁系统数学模型,如图2所示。

图2 励磁系统数学模型

1.2 设计电磁耦合结构

为了实现电网定向电压励磁的自适应调控，需要构建电磁耦合结构。本文将永磁同步发电机与普通电励磁电机相结合，使得转子上的永磁体提供励磁磁通，且定子上也会通过直流励磁绕组产生一定的磁通[10-11]，实现在气隙中的合成。定子结构,如图3所示。

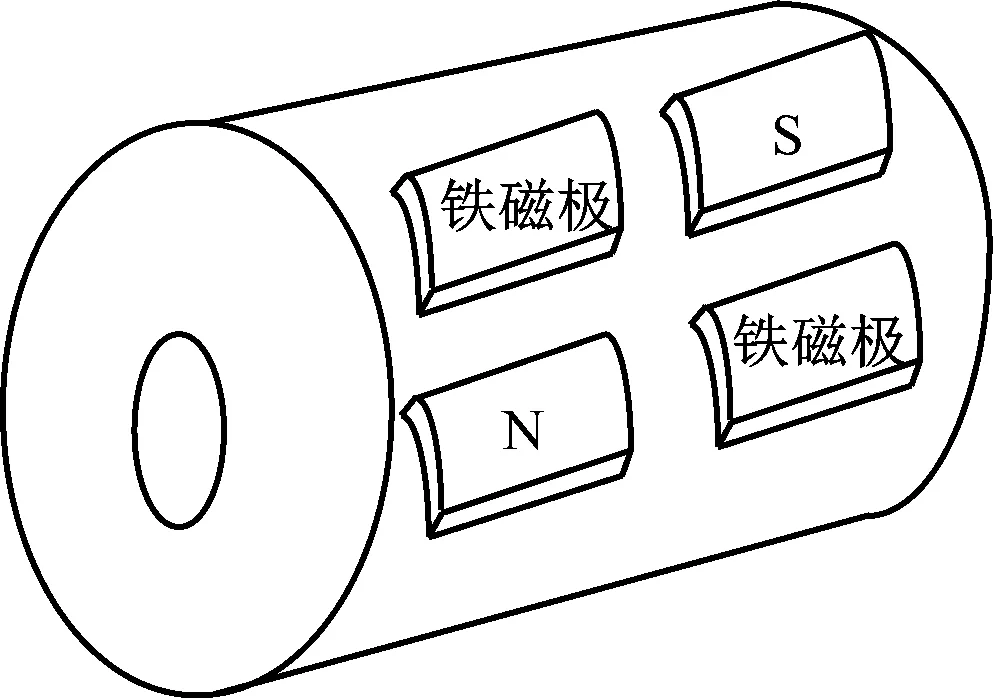
图3 励磁定子结构

由图3可知，定子具有三相对称绕组结构，被环形直流励磁绕组分成两部分，两端铁芯通过背轭在机械和电磁上连接，极端上由同极磁体和铁磁极交错排列。当磁极展开后直流励磁电流存在3种情况。3种情况下的合成气隙磁场,如图4所示。

图4(a)表示励磁电流为0时气隙磁场的分布;图4(b)表示励磁电流大于0时气隙磁场的分布;图4(c)表示励磁电流小于0时气隙磁场的分布。当励磁电流为0时，只有永磁体磁场存在;大于0时，铁芯级和永磁体磁场方向是相同的，这样增强了轴向磁场，导致气隙内的有效轴向磁场减弱[12-13];小于0时则相反，这种电磁耦合结构能够在发电机工作过程中能够感应到AVR反馈系数的变化，为励磁调控奠定基础。至此完成电磁耦合结构的设计。

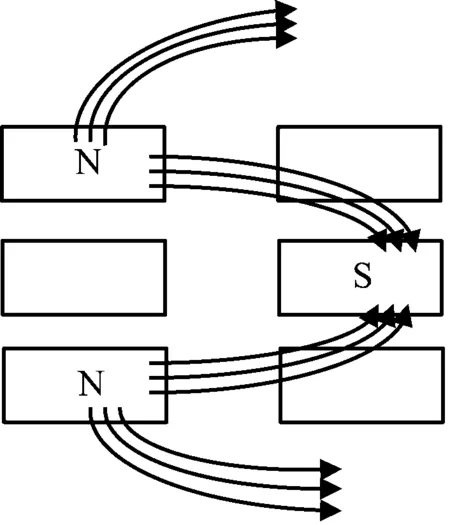
(a)

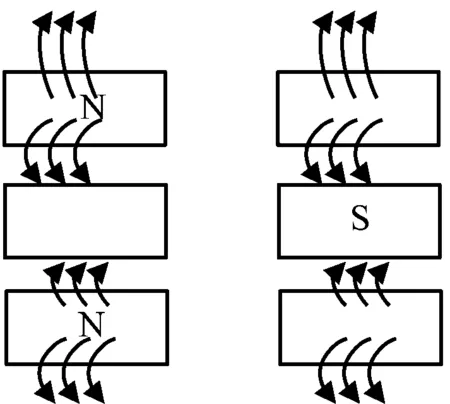
(c)

1.3 优化励磁调节器

在自适应调节过程中，主要使用蚁群算法来完成调控。传统的蚁群算法会设定参数作为初始值，但是可能会丢失最优解，本文将初始值设定为随机生成的n条路径，能够在更大范围内筛选，全局搜索最优解。并根据搜索过程中路径分布均匀度，实现动态的自适应调整信息素浓度，分布均匀度需要通过聚度来衡量[14-15]。当路径上的蚂蚁比较分散时，聚度就比较小，这个时候搜索速度比较慢，且难以强化最优信息。当聚度比较大时，容易早熟停滞。因此要想获得比较好的调节效果，要掌握好聚度的大小。当有m只蚂蚁从某节点x到另外的若干节点中，有r条路径可以选择，那么在上一次迭代过程中，这r条路径上的蚂蚁数分别为a1、a2、…、ar，那么节点x的聚度,如式(5)。

(5)

设r条路径中，有蚂蚁经过的路径数量为s，那么节点x的聚度会随着s的减少而增大。当聚度过小时，需要对正反馈信息进行强化，增大数量较少的较优路径被选取上的概率，增大信息素权重；当聚度过大时，要使解多样化，使较多的路径被选取上。通过这样的动态自适应调节，能够改善蚁群搜索速度，对于励磁系统的电压控制效果更佳理想。当节点聚度较大，说明上次迭代过程中，从该节点到另外节点的路径比较集中，也就是说信息量比较集中，在路径选择过程中，蚂蚁会考虑信息浓度最高的路径，因此需要对蚁群路径转移进行合理化约束，需要计算能见度,如式(6)。

(6)

式(6)表示的含义是：第k只蚂蚁在上次迭代时的路径为path(k,i)，那么这次迭代时，横坐标在i时，纵坐标所有点j的能见度。在实际的应用中，设定蚁群总数和信息素等相应数量，随机生成路径，对各点的信息素浓度进行调整更新，设置最大迭代次数，计算路线转移概率，最终提取到最优参数。至此完成基于电磁耦合的电网定向电压励磁自适应调控方法的设计。

2 发电机组励磁仿真实验

2.1 设计仿真环境

仿真实验主要对空载阶跃、空载短路以及功率因数为0.98时阶跃、短路进行实验。为了更好地检测本文调控方法的有效性，本文的仿真测试以某电厂为原型，将其在仿真软件中进行简化，发电机为水轮机组。系统的结构,如图5所示。

如图5结构所示，从A点到D点的电路为500 kV，在仿真中，将D点等值为无穷大的母线，另外变电站C是A送电的主要输出电，C的总负荷,如式(7)。

PC=(R+jX)+(PL+jQL)

(7)

式中，R+jX表示恒阻抗负荷;PL+jQL表示恒功率负荷。发电机的参数,如表1所示。

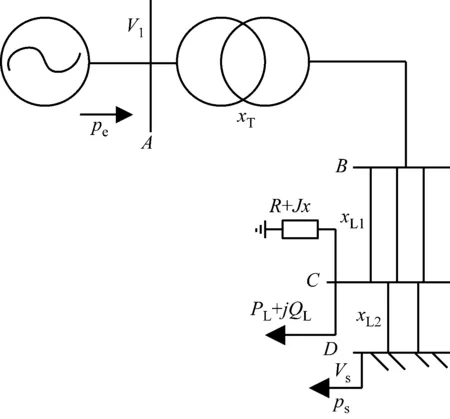
图5 简化的测试系统结构图

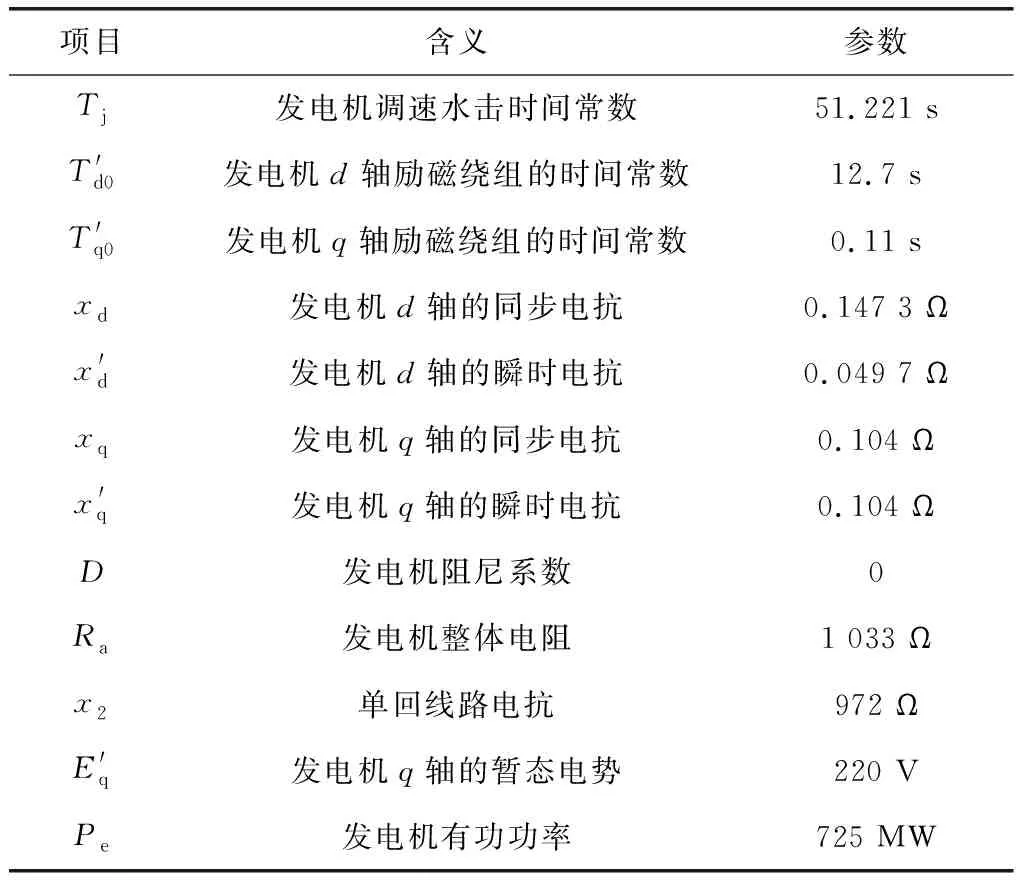
表1 发电机参数

仿真模型中，励磁机类型为自并励可控硅静止快速励磁，时间常数为0.04,励磁的极值为4.7。试验过程中，设置空载仿真时间为40秒，负载仿真时间为60秒。仿真参数选取水轮机组的实际参数，在空载试验中，在1秒时施加10%的电压正向阶跃，15秒时施加10%的电压负向阶跃，30秒时令机端三相接地短路，保持这种故障状态时间为0.1秒；在负载实验中，令功率因数为0.98,1秒时施加5%正向电压阶跃，12秒时施加10%负向电压阶跃，间隔10秒后施加5%正向电压阶跃回到平衡点，30秒时令机端三相接地短路，保持这种故障状态时间为0.1秒。上述实验过程中，分别使用本文设计的调控方法和传统PID调控方法进行实验，并将实验结果进行对比。

2.2 实验结果对比分析

经过两组典型的仿真测试，得到两种调控方法的实验结果,如图6所示。

图6(a)为额定负载情况下，功率因数为0.98时的试验结果;图6(b)为空载实验结果。根据图6能够得到实验结果各项数据的报表,如表2所示。

从得到的实验结果可以看出，传统的PID调控方法虽然电压没有出现震荡和超调的情况，但是上升时间较慢，与国标要求的0.6s相差较大，本文设计的调控方法各项性能均达到要求，这是因为电磁耦合过程中能够感应到AVR的反馈系数，完成了整体参数的调控，且本文调控的阻尼比更大，电压恢复较快，尤其在短路情况下更加明显。综上所述，本文设计的调控方法对于调控电压方面的性能要优于PID调控方法。

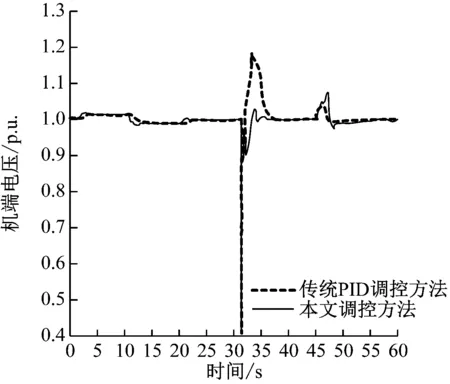
(a)

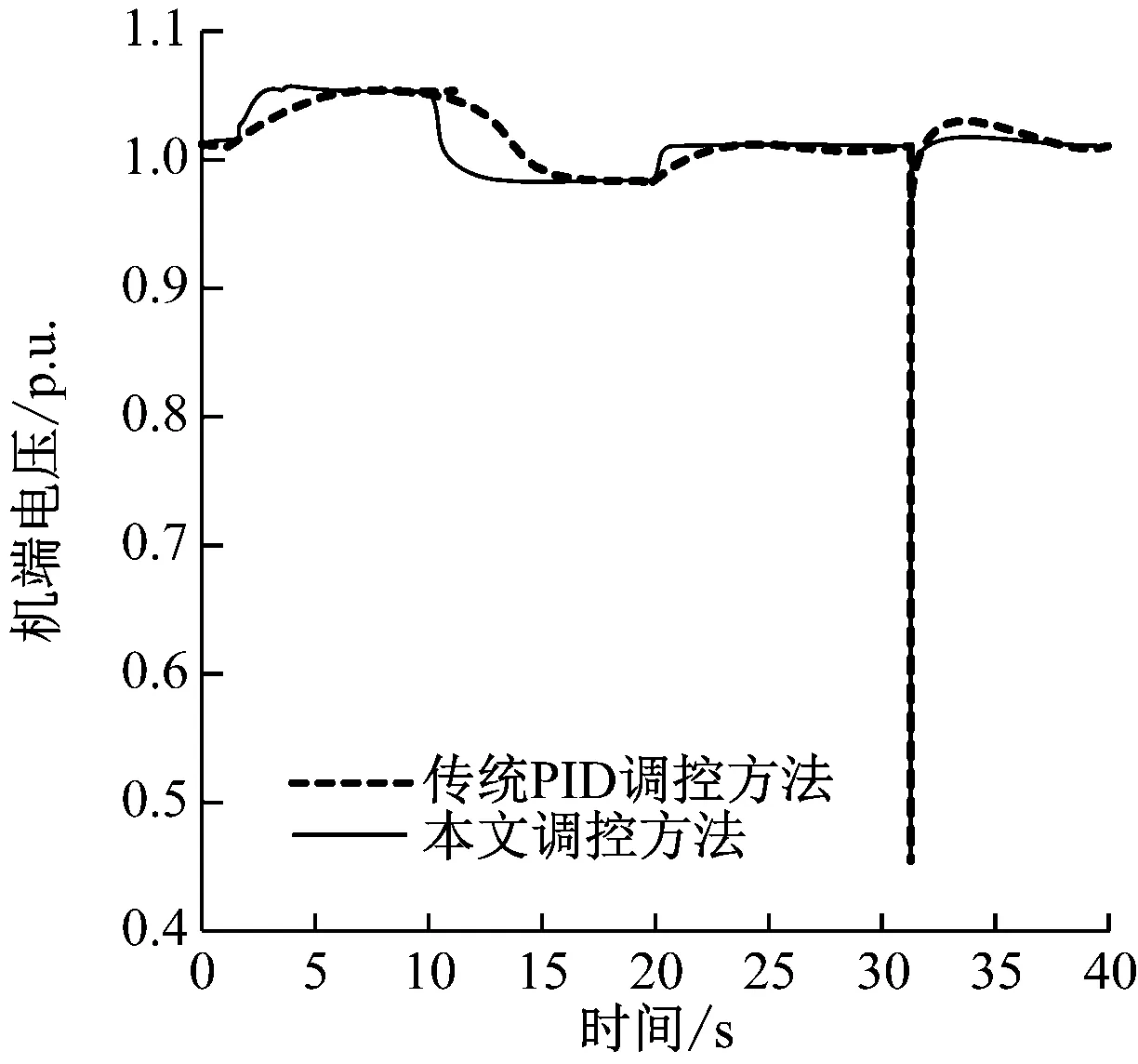
(b)

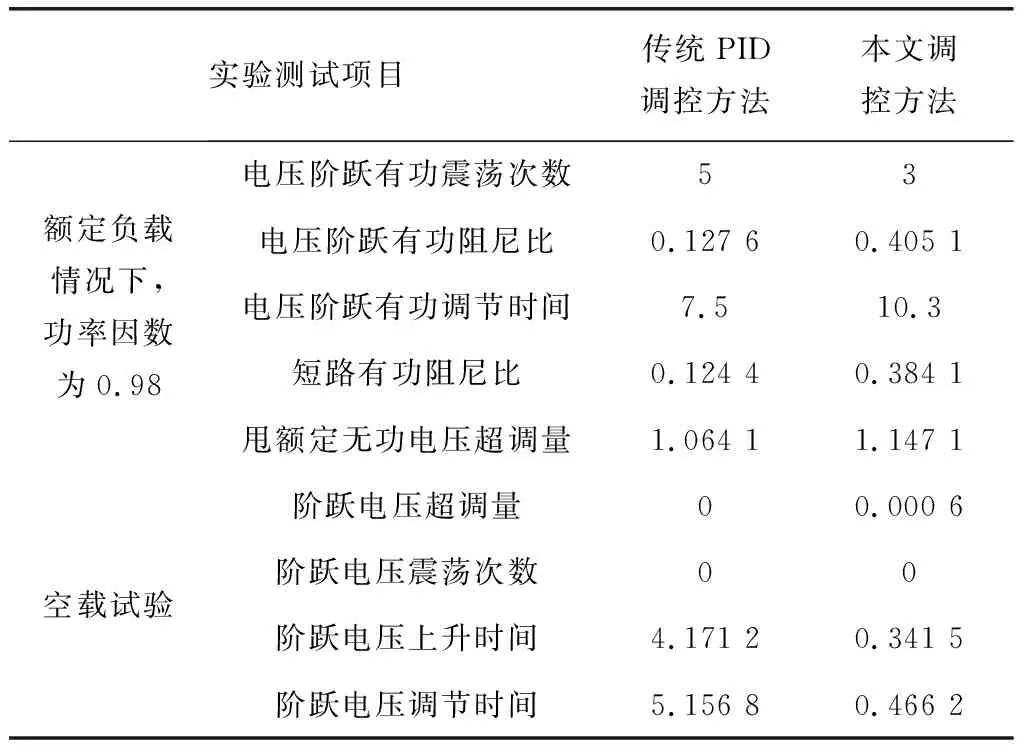
表2 实验结果表

3 总结

电力系统安全稳定运行是发电机组的基本需求，为了保证电力系统在受到外界干扰时，具有较高的抗干扰能力，需要在电网中加入励磁系统来平衡控制电压。本文针对励磁调控方法存在的一些弊端，设计了一种基于电磁耦合的电网定向电压励磁自适应调控方法。通过实验结果表明，本文设计的方法能够在外界干扰的条件下保证电压的稳定。但是本文仍然存在一些不足之处，希望在今后的工作中能够逐步完善。