基于滤波器方法主动吸收式数值水槽研究

刘 宣，白志刚，余海涛，高树军

(天津大学 建筑工程学院，天津 300350)

波浪水槽是研究波浪传播及其与结构物直接相互作用的重要手段之一，具有直观、可靠等优点。其缺点是成本高、过程复杂同时还可能存在比尺问题。随着计算机技术的发展和计算流体力学理论的进步，基于N-S方程建立的粘性数值水槽得到了迅速发展，在模拟波浪破碎、旋涡，波浪与建筑物相互作用等方面问题有着很好的应用。Miyata[1]等采用MAC法追踪自由面，有限差分法离散N-S方程，建立二维数值波浪水槽。Phung[2]基于VOF法建立两相流数值模型，并将其应用于波浪与潜堤的相互作用以及波浪在斜坡上破碎的数值模拟。Lin[3]通过求解雷诺时均方程，采用k-ε模型模拟紊流作用，实现了孤立波和椭圆余弦波的数值模拟。王永学[4]采用VOF法捕捉自由表面，利用雷诺时均模型模拟波浪在直立墙前的破碎过程，得到直墙面上波压力。齐鹏和王永学[5]基于VOF法建立三维数值波浪水槽，设置动网格造波边界，较好地模拟了规则波和结构物的相互作用。李胜忠[6]基于FLUENT软件建立二维数值波浪水槽，很好地完成了线性规则波、Stokes波、孤立波以及不规则波的模拟。

但无论是物理实验还是数值模拟，受到波浪水槽长度和宽度影响，造波板产生的行进波在遇到结构物后会发生一次反射，一次反射波与原行进波叠加后传递到造波板上会发生二次反射。因此在进行一段时间的造波后，水槽内波浪的多次反射、叠加将严重影响实验精度。Salter[7]等以摇板板上所受波压力为反馈信息，设计递归式滤波器，对造波板的速度进行调整，以解决二次反射的问题。Bullock 和 Murton[8]以板上波高信号为反馈信息，不考虑造波板前的衰减驻波和波浪非线性的影响设计了递归式滤波器，得到造波板的位移，在物理水槽中实现了楔形造波机规则波和不规则波的主动吸收式造波测试。国内方面，陈汉宝[9]等根据势函数计算造波机参数，探讨了无反射造波机的实现思路。柳淑学[10-11]等提出代表频率时域控制法用于不规则波的主动吸收，实现了推板式造波机不规则波的主动吸收式造波实验。顾民[12]等采用频域滤波器方法设计完整具有主动吸收功能的造波装置，实现了摇板式造波机规则波和不规则波主动吸收式造波实验。李宏伟[13]在时域控制法和频域滤波器方法的基础上，设计了基于S面控制的主动吸收造波系统。杨洪齐[14]在时域和频域两个方向实现了规则波和不规则波的主动吸收，提出了带有延时补偿的主动吸收控制方程，提高了造波质量。

将滤波器方法应用在主动吸收式造波中，可以针对不同频率的波浪做出不同的反应效果，对不规则波有着更好的吸收效果。但同时由于滤波器方法对频率的敏感特性，很容易受到横波、不规则杂波等问题影响，经常会出现造波板异常抖动、造波质量较差等问题。通过数值模拟方法可以更好地验证设计滤波器主动吸收效果，但目前主动吸收数值波浪水槽[15-16]大多采用时域控制主动吸收算法，滤波器方法在数值模型中很少涉及。本文基于开源软件OpenFOAM，利用动网格技术模拟推板式造波，自定义滤波器主动吸收式造波边界，建立粘性水槽数值模型验证滤波器方法的准确性和可靠性，为物理模型实验提供参考。

1 数值水槽基本方法及理论

1.1 黏性波浪数值水槽的控制方程

采用VOF方法追踪自由表面，其原理是定义项体积分数α，当α=0时表示该网格内均为空气，当α=1时表示该网格内均为水，当0<α<1 时表示为空气和水的交界面。二相流的平均密度和动力粘性系数为

ρ=αρ1+(1-α)ρ2

(1)

μ=αμ1+(1-α)μ2

(2)

故黏性数值水槽的控制方程包括连续性方程、包括项体积分数的动量方程和体积分数函数。

连续性方程

·U=0

(3)

动量方程

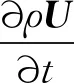
(4)

体积分数函数

(5)

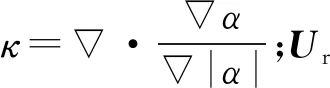
1.2 推板造波理论

(6)

根据线性叠加法，不规则波波面可由有限个规则波波面线性叠加而成

(7)

N为规则波的数量，φi为随机初相位，位于[0，2π]内，Ai为第i个规则波的振幅，其表达式为

(8)

式中：ωi为第i个组成波的代表频率；△ωi为频率间隔；S(ωi)为代表频率为ωi下的谱能密度。

根据线性造波理论，不规则造波时推板式造波板的位移为

(9)

1.3 频域滤波器主动吸收理论

造波板运动产生的波浪传播到建筑物上发生一次反射，一次反射波与原行进波叠加后传递到造波板上会发生二次反射，所以在进行一段时间的造波后，水槽内的波浪经过多次反射、叠加后对试验精度产生较大影响。主动吸收式造波是在造波板原有位移上添加一个修正位移来消除二次反射波，在水槽内得到稳定波场。造波板的位移可以用下式表示

x=xp+xa

(10)

造波板上波面为

η0=ηp+ηa+ηps+ηas+ηr+ηrr

(11)

式中：η0为造波板上实测的总波高；ηp和ηa为由xp和xa所产生的行进波；ηps和ηas为xp和xa所产生的非传播模态项；ηr为水槽中的反射波；ηrr为在造波板上产生的二次反射波。在满足主动吸收的条件下，有

ηa+ηrr=0

(12)

由此联立方程推导出频域传递函数为

(13)

式中：C0为水动力传递系数；ECn为推板前驻波影响因子，分别与波数k0、虚波数kn和水深h有关。

得到的F即为主动吸收式造波系统的主动吸收传递函数，故滤波器法主动吸收系统可以认为是一个输入为2ηp-η0，输出为x，频率响应特性为F的单输入、单输出的线性时不变系统。

2 滤波器设计

对于一个典型的单输入、单输出的离散线性时不变系统，可用线性常系数差分方程来表示

(14)

将上式的N阶线性常系数差分方程变换形式，取a0=1得

(15)

已知一个离散时间系统可用式(15)的差分方程表示，则在z域中系统函数可表示为

(16)

在主动吸收系统中，输入信号为目标波高与实测波高的差值，是一个有界量；输出信号为造波板位移，受到造波板幅值限制也是有界的。从定义上说，如果输入有界，则输出必定有界的系统是稳定的，因此频域滤波器的设计也应满足稳定性要求。但由于IIR滤波器系统函数存在分母项，故存在极点，有不稳定的可能。从定义上看，系统稳定的充要条件为系统的单位脉冲绝对可加和，即对于一个稳定系统，存在正数B使得

式中：h(n)为系统的脉冲响应。对于存在极点的滤波器系统，一般常用单位圆方法对系统稳定性进行判断。当极点落在单位圆外时，表示滤波器当前输出需要放大上一时刻的输出，当n→∞，系统的脉冲响应趋于无穷大，不满足绝对可加和条件。当极点落在单位圆上时，当n→∞，系统的脉冲响应趋于常数或等幅值震荡，不满足绝对可加和条件。当极点落在单位圆内时，表示滤波器当前输出需要缩小上一时刻的输出，当n→∞，系统的脉冲响应趋于零，满足绝对可加和条件。对于有多个极点的系统，可根据代数学知识进行分解，将其看做多个单极点并联而成的系统。在并联系统中，只要有一个系统不稳定，整个系统就是不稳定的。因此系统稳定的充要条件为滤波器的极点均落在单位圆内。

滤波器采样频率定义了滤波器每秒从输入信号中提取并组成离散信号的采样个数，所以滤波器的采样频率应小于或等于输入信号——波高传感器的采样频率。本文以天津大学创新研究院的波流水槽作为工程背景，其采用波高仪的采样频率为1 000 Hz，适当减小采样频率在实验室造波实验中会给上位机更多的时间对信号进行处理，保证在每个时间间隔内给出造波板的位移信号；在数学模型实验中可以适当增大时间步长、提高计算速度，因此本文滤波器设计频率选为250 Hz。

本文通过求解色散方程得到不同水深下，C0、ECn与频率的关系，进而得到理论传递函数。采用基于线性最小二乘法(OLS)，选择带控制量的自回归模型(ARX)作为拟合模型对理论传递函数进行模拟。理论上，滤波器阶数越高，拟合精度越高，但同时系统不稳定、计算量增大、延迟问题也会更加明显。并且由于理论传递函数在低频处幅值响应十分大，如果对过低频率的波浪进行主动吸收会导致造波板位移超过造波机限制，无法进行正常造波。而在本文工程背景下，不需要对0.2 Hz以下规则波进行主动吸收，0.2 Hz以下波浪在不规则波的能量占比也较小，故根据实际需要，设计二阶滤波器在低频处对幅值进行抑制，在常用实验造波频率0.3～2.5 Hz范围内进行拟合。

本文通过ARX方法得到在0.5 m水深下主动吸收滤波器参数后首先对滤波器进行稳定性检测，要保证滤波器所有的极值均落在单位圆内。如图1所示，其中×代表极点，○代表零点，两极点坐标分别为(0.998 4,0)和(0.955 4,0)，所有的极点均落在单位圆以内，系统稳定。其次要对滤波器使用要求进行检测，如图2所示，滤波器在低频处对幅值进行抑制，在常用造波频率范围内拟合程度良好，满足实验要求。

图1 滤波器零极点分布图

3 自定义造波边界

根据OpenFOAM自带的网格运动边界基类fixedValuePointPatchFields开发新的滤波器主动吸收式造波边界类。此边界包括私有数据时间序列、波面序列、滤波器阶数和滤波器系数等。根据字典文件读取关键字来得到以上私有数据。通过字典文件读取时间-理论波面序列，得到当前时刻的理论波面。通过VOF方法得到边界上的水深，减去初始水深得到造波板上波面。根据滤波器阶数和参数设计滤波器，以理论波面和实际波面为输入量，通过储存之前的位移及波面，根据IIR滤波器原理，利用差分方程计算得出当前造波板位移。

4 数值水槽的建立及验证

4.1 数值水槽的设置

本文以天津大学创新研究院的波流水槽作为工程背景，如图3所示，根据实际水槽条件建立一个长9 m、高0.8 m、水深为0.5 m的二维矩形水槽模型。根据查晶晶[18]推荐,网格长宽比不应该超过20∶1，垂向波高内网格数不应少于10个，纵向波长范围内网格不应少于40个，故在X方向布置500个网格，在Z方向布置300个网格。左侧为造波边界，右端为全反射墙体边界。根据滤波器的采样频率，时间步长选为0.004 s。据水槽左端3.17 m、3.47 m、3.83 m处分别设置监测点，得到该位置上的波面-时间曲线。在相同的波浪要素条件下，分别进行主动吸收造波和普通推板造波数值对比实验，对结果进行分析处理，验证滤波器法主动吸收的正确性。

图3 数值波浪水槽示意图

4.2 规则波的验证与对比

规则波数值模拟时长定为60 s，目标波形为余弦波。分析对比1号测点上主动吸收造波和普通推板造波波面曲线。从图4中可以看出主动吸收式造波时，入射波在到达水槽右端后形成一次反射波，入射波和一次反射波叠加后传递到造波板时，造波板有效吸收了二次反射波，此时水槽内只有入射波与一次反射波，二者叠加形成稳定驻波。而采用普通推板式进行造波，波浪发生多次反射，无法形成稳定波场。证明了频域滤波器方法对规则波的主动吸收效果十分显著。

4-a T=1.0 s,H=0.04 m 4-b T=1.5 s,H=0.04 m

4.3 不规则波的验证与对比

不规则波主动吸收造波模拟时间为120 s，靶谱选为JONSWAP谱，根据1、2、3号测点上波面情况根据三点法进行入反射分离得到入射波波面曲线。与普通造波时入射波波面对比如图5所示。从图中可以看出开启主动吸收时波峰波谷较普通造波时小，即能量较正常造波时小。初步说明频域滤波器法主动吸收能够对二次反射波进行有效吸收，波场内波浪不会发生多次反射，能量不会反复叠加。

5-a T=1.0 s,H=0.04 m 5-b T=1.5 s,H=0.04 m

为进一步说明滤波器法主动吸收式造波对二次反射波的吸收效果，分别对主动吸收造波和普通造波入射波面进行频谱分析，得到的频谱和目标靶谱对比如图6所示。可以看出开启主动吸收时频谱曲线与靶谱拟合较好，普通造波时谱峰密度远大于靶谱，说明波浪多次反射叠加后能量较大、波场混乱。

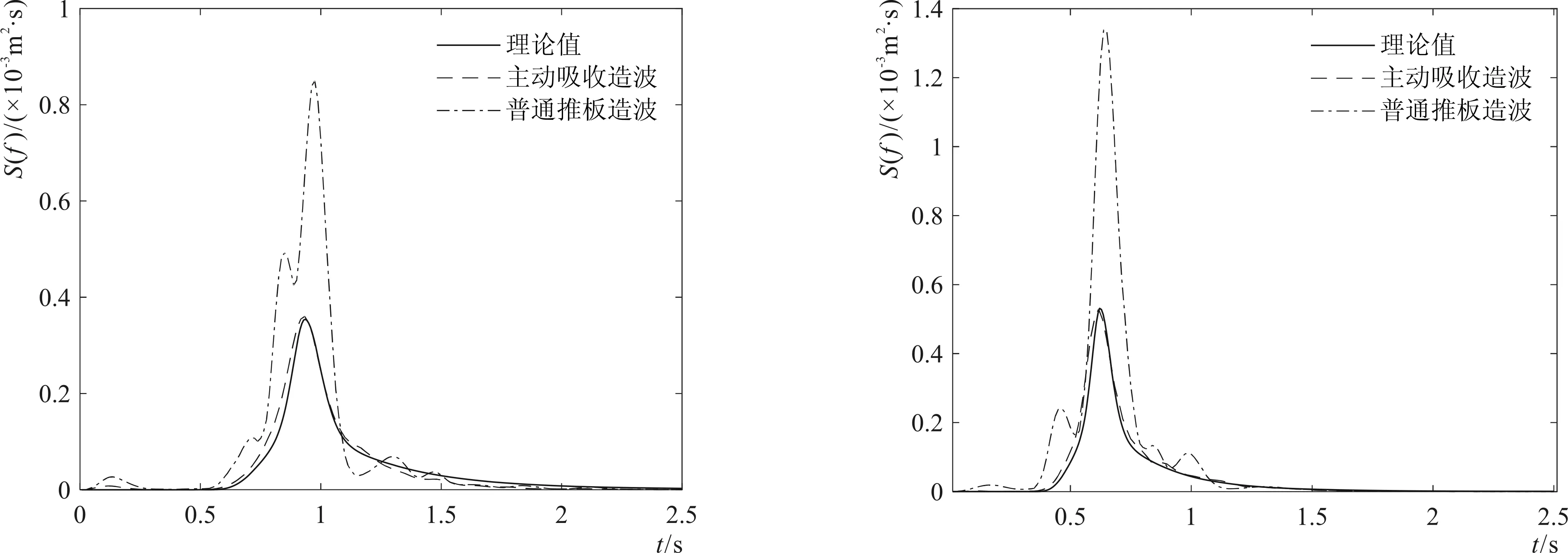
6-a T=1.0 s,H=0.04 m 6-b T=1.5 s,H=0.04 m

为定量分析滤波器法对不规则波的吸收情况，参考王先涛[19]的分析方法定义主动吸收率，根据主动吸收造波前后频谱曲线面积对比来判断吸收效果。主动吸收率ra计算公式如下

(17)

式中：Sp为正常造波频谱曲线；Sa为主动吸收式造波频谱曲线；Sn为理论频谱曲线。

同时分析对比特征周期、谱峰波高、谱峰密度来验证不规则波模拟精度。表1为滤波器法主动吸收造波入射频谱曲线的特征参数与靶谱特征参数的统计结果。不同周期下的特征周期T1/3、谱峰波高Hp和谱峰密度Sp误差均小于3%。在1.5 s周期下，可能普通推板造波时能量较小导致吸收率与其余各组相比较低，为91.15%。其余各个周期下的吸收率均超过95%。综合考虑各类波浪要素和吸收率，进一步说明滤波器法对不规则波有着良好的吸收效果。

表1 不规则波波浪要素统计结果

5 结论

本文基于OpenFOAM 不可压缩二相流求解器interDyMFoam，开发了仿物理造波数值水槽，实现了滤波器法主动吸收式造波。通过继承动边界类fixedValuePointPatchField开发了滤波器法主动吸收造波边界。结合工程背景需要，确定了针对目标水深下的IIR滤波器参数。

在不同周期规则波的造波实验中，滤波器法有效吸收了二次反射波，能够得到稳定波场。在不同周期不规则的造波实验中，波浪要素与靶谱目标参数误差均小于3%，滤波器法对二次反射波的吸收率均在90%以上。对比不同周期下规则波和不规则波造波效果，可以看出滤波器方法对规则波和不规则波的二次反射都有着良好的吸收效果。为后续滤波器方法在物理模型实验的研究提供了重要基础依据。同时滤波器方法将主动吸收问题从时域映射到了频域内，可以通过对理论函数曲线拟合的不断优化，为解决实际造波问题提供了更多可行的方向，也为解决三维水池主动吸收造波问题做好铺垫。