毗邻互通立交特长隧道交通组织方法

马兆有，方守恩，刘 硕,苏东兰

(1．道路与交通工程教育部重点实验室(同济大学)，上海 201804；2．道路交通安全公安部重点实验室公安部交通管理科学研究所)，江苏 无锡 214151； 3.苏州科技大学 土木工程学院，江苏 苏州 215011)

特长隧道作为道路网中的一个特殊路段，受交通流量增加、车辆运行速度较快和独特封闭环境的影响，使其成为了潜在的事故多发路段[1]. 据统计，2015年至2019年全国隧道路段共发生交通事故4 039起，造成1 274人死亡、4 435人受伤，年均发生事故807.8起、导致254.8人死亡，分别占全国交通事故总数的0.37%和0.41%. 隧道事故死亡率为0.32人/起，是同期全部道路交通事故死亡率的1.14倍[2].

为了保障行车安全，特长隧道通常采取禁止车行道变换的交通组织方式[3]. 对双洞多车道的特长隧道而言，简单地禁止车行道变换，可能因交通流中慢车的影响导致通行效率降低，甚至引发排队、缓速通行等问题；同时，也会因车辆通行需求和动力性能的差异，导致交通流车速离散性较大，增加违法变道行为发生几率，影响特长隧道的运营安全. 此外，由于地形限制或规划未预留足够空间等因素的影响，经常会出现特长隧道与互通立交之间的间距较小的特殊情况[4]，进出主线的车辆产生在隧道内完成车行道变换的客观需求. 同时，从驾驶人的行为特征来看，由于特长隧道里程较长，禁止车行道变换可能会降低驾驶人的注意力，因疲劳驾驶或疏忽引发交通事故. 本文基于特长隧道交通安全影响因素出发，结合特长隧道变道通行的交通需求，兼顾行车安全和通行效率，探讨特长隧道不同区段的交通组织和控制方式[5].

1 变道约束条件分析

根据车辆变道的交通需求，可将变道行为划分成强制性变道和判断性变道两类. 强制性变道是指必须发生的车道变换行为，如车辆为完成转向或其它操作而必须进行的变道行为，该行为多发生在匝道入口、立体交织区等特定路段. 判断性变道是一种选择性的车道变换行为，是驾驶人为了获得更大的行驶空间或更高的行驶速度而采取的一种车道变换行为. 在特长隧道出口外无匝道连接时，车辆变道行为属于判断性变道，有匝道连接时还包含强制性变道，毗邻互通立交的特长隧道同时存在强制性变道和判断性变道的交通需求[6].

1.1 变道最小距离模型

车辆在变道过程中受重力、摩擦力和离心力的综合作用，受力情况如图1所示.

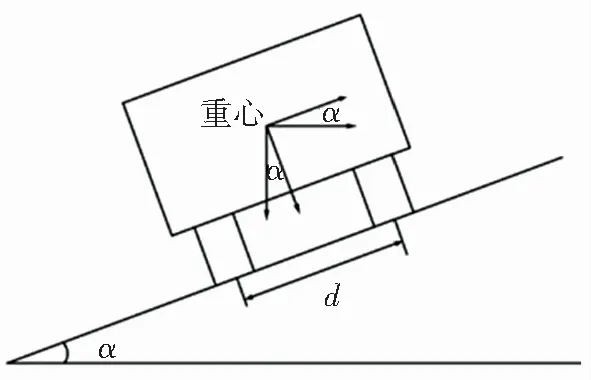
图1 车辆变道过程受力图

1.1.1 防侧滑最小转弯半径

当摩擦力小于重力和离心力合力时，车辆将发生横向侧滑，防侧滑稳定性约束条件为

(1)

对于普通路段而言，超高值较小，sinα≈i，则防侧滑最小转弯半径简化为

(2)

式中：m为车辆质量，kg；v为运行车速，km/h；μ为路面摩擦系数；ih为路拱横坡.

1.1.2 防侧翻最小转弯半径

在离心力作用下，车辆存在以外侧车轮中心为转轴发生侧向翻转的倾向，防侧翻稳定性约束条件为

(3)

防侧翻最小转弯半径简化为

(4)

式中：v为车速，km/h；b为车辆轮距，m；e为曲线超高；h为车辆重心高度，m. 根据常见货运车辆的参数，b取2.00 m，h取1.70 m.

1.1.3 最小车头时距

车辆变道还受目标车道可插入间隙的影响[7]，即变道车辆n应满足不与目标车道上的前车n-1和后车n+1发生碰撞，其安全约束条件为

(5)

(6)

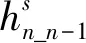
基于运行安全和通行效率考虑，将车辆n与前车n-1的最小车头时距模型作为车辆变道的安全模型：

(7)

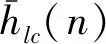
1.1.4 最小变道距离

假设车辆在变道过程车速方向发生变化，而车速大小保持不变，围绕两个半径相同的连续反向圆曲线S1和S2做匀速圆周运动[8]，如图2所示. 将车辆变道抗滑临界圆曲线半径、抗侧翻临界圆曲线半径作为安全约束条件，界定车辆变道临界安全状态.

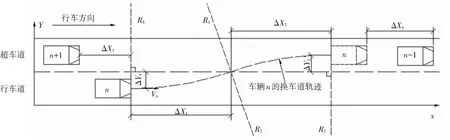
图2 车辆变道过程行驶轨迹示意图

车辆在变道过程中绕行的两个圆曲线半径为R，发生的横向位移为ΔY1和ΔY2、纵向位移为ΔX1和ΔX2，则最小变道距离记为

(8)

考虑目标车道插入间隙的影响，最小变道距离为

(9)

式中Δlmin为考虑目标车道插入间隙影响的最小变道距离，m.

1.2 安全变道概率模型

当特长隧道与互通立交连接段的长度较小时，提供给车辆进行变道的距离有限，基于最小换道距离模型，研究建立特定条件下车辆安全变道成功概率[9].

1.2.1 单次安全变道概率

车辆在变道过程中受交通流量、相邻车道车辆相对速度的影响，为考虑相邻车辆及连接段长度对变道成功概率的影响，构建安全变道概率模型，以安全变道系数ap,v评价变道的安全性.

假设交通流在特长隧道内随机、均匀分布，则平均车头时距可表示为

(10)

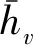
某时刻变道车辆成功变换到目标车道的车头时距间隙hs可表示为

(11)

式中p为单次安全变道概率.

安全变道系数ap,v可表示为

(12)

式中：hsn-1为前车n-1与变道车辆n之间的安全车头时距，s；hsn+1为后车n+1与变道车辆n之间的安全车头时距，s.

在保障前后车安全距离的情况下，单次安全变道概率p为

(13)

1.2.2 二次安全变道概率

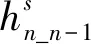
(14)

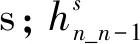
基于车辆变道前的调整时间及连接段允许变道总时长，构建保证以安全距离变道成功的概率计算模型：

(15)

式中：pt为连接段保证以安全距离变道成功的概率，p为某时刻以安全系数ap,v变道成功的概率，t表示连接段允许变道总时长，⎣x」表示对x向下取整.

由于车辆两次变道之间相互独立，则连续两次安全变道概率可表示为

(16)

2 交通组织方案类比分析

根据特长隧道出口外侧一定距离内是否存在匝道出口，可将特长隧道洞口外侧连接段的衔接方式分为两类：1)不存在匝道出口，车辆不需要考虑变道进入特定的车道以进入匝道出口，只存在判断性变道；2)存在匝道出口，当隧道内禁止变道、连接段长度不足以供车辆完全变道进入匝道出口，车辆可能会在分流点前降低车速通过强行变道进入出口匝道，或在隧道内禁止变道区段违法变道进入目标车道；当隧道内允许变道，车辆可以在隧道内完成车道变换进入目标车道.

2.1 仿真试验设计

借助Vissim仿真技术，以某座双洞6车道快速路特长隧道为例，阐述典型交通组织方式比选方法. 该隧道全长为7.9 km，设计速度为80 km/h，平纵断面线形条件较好，南侧出口距互通立交匝道渐变段起点为380 m，中小客车、大型货车、大型客车交通流比例为43.25∶38.04∶3.65，不同阶段交通流量组成见表1. 假设大型车分布在右侧两个车道，小型车从内往外3个车道分别占60%、20%、20%，去往期望方向时发生的变道次数尽可能少且均匀分布. 隧道洞口至连接段的车道数为3，通往城区、远郊方向的匝道数均为2.

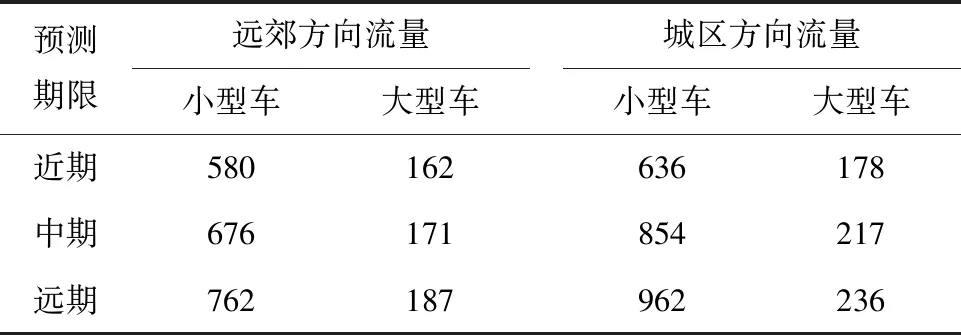
表1 交通流量组成

在仿真试验中，交通流量为600～3 000 pcu/h，相邻流量之间的梯度设为800 pcu/h. 选取小型车和重型货车两种车型，设定小型车交通流量占比50%～100%，相邻比值间的梯度为10%. 结合特长隧道的行车环境特点，设计4种典型交通组织方案：方案1，隧道内允许变道，最内侧车道为小型车专用道，外侧两条车道为大小型车混行车道；方案2，隧道内允许变道，不设置专用车道；方案3，隧道内禁止变道，最内侧车道为小型车专用道，外侧两条车道为大小型车混行车道；方案4，隧道内允许变道，最内侧车道小型车专用道，中间车道为大小型车混行车道，最外侧车道为大型车专用车道.

2.2 交通组织方案比选

选用平均速度、车均延误评价车辆的通行效率，车道变换次数指标评价车辆的安全性，分析不同交通组织方案在高峰交通流量分别为600、1 400、2 200、3 000 pcu/h，小型车占比分别为50%、60%、70%、80%、90%、100%等条件下的通行效率和安全性. 在交通流量设定为2 200 pcu/h时，特长隧道内交通流量密度处于正常范围，对应的交通服务水平较高，本文仅以2 200 pcu/h流量条件下，不同组织方案特征指标类比分析为例.

如图3所示，在交通组成相同的情况下，平均速度随着交通量的增长而降低，随着小型车比例的增加而提升，采用平均速度作为评价指标时方案1最优. 方案2平均速度的变化随着小型车比例的增加而近似服从线性变化，其优势区域在小型车流量占比为80%～100%之间. 方案3平均速度随着小型车比例的上升增长速度较快，且随着交通量的增大上升越加明显[10]. 方案4在小型车比例小于80%的情况下平均速度高于方案2，在大型车流量较高(20%～50%)时平均速度随小型车比例上升增幅较小.

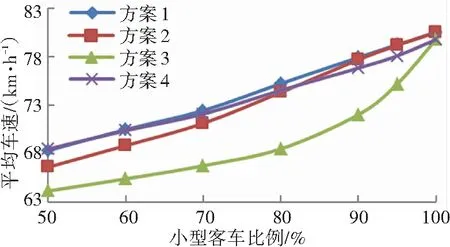
图3 平均速度-交通组成变化

如图4所示，不同交通组织方案下的车均延误均随着交通流量的增长而增加，方案1在各种交通流量和交通组成条件下获得的车均延误最低. 方案2车均延误随着小型车比例的增加而逐渐减少，在小型车比例在80%～100%之间时获得的车均延误较低，是方案2最理想的交通构成区间. 方案3车均延误是各种交通组织方案中最大的，随着交通流量的增大交通流密度变大、每辆车拥有的行驶空间和驾驶自由度降低，大型车后面跟驰行驶而不能超越的车辆逐渐增多，当交通流中重型货车达到一定比例时交通流运行的阻隔作用最大. 方案4车均延误在小型车比例为70%～80%之间时出现一个最大值，在小型车比例为50%～80%之间，得到的车均延误仅高于方案1.

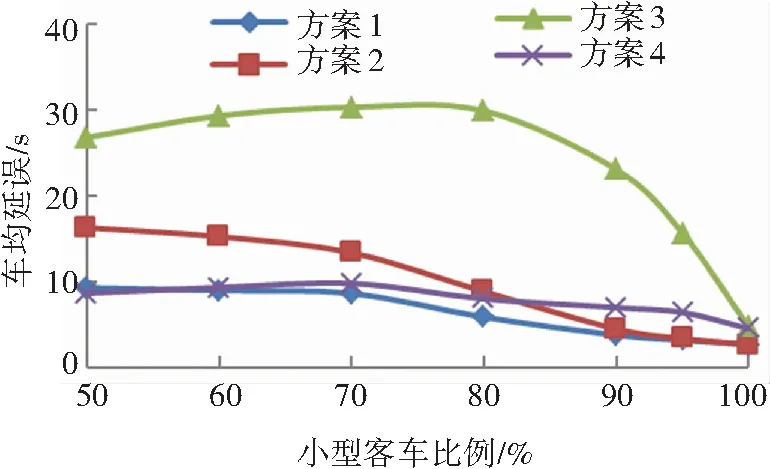
图4 车均延误-交通组成变化

如图5所示，车均变道次数与交通流量之间变化并非呈现简单的正相关或负相关的关系，在交通流量很小的情况下，车辆不需要进行车行道变换就可以保持较高的行驶自由度. 随着交通流量的进一步增大，期望进行车行道变换的车辆数增多，但由于交通流密度较大，可穿越间隙减少，车行道变换难度增大，车均变道次数减少.

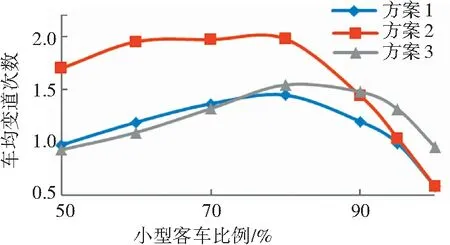
图5 车均变道次数-交通组成变化

如表2所示，在分析案例中采取最内侧车道禁止大型车行驶，外侧两条车道任意车行道变换的交通组织方式，可获得隧道交通流运行安全和通行效率的最优化[11].

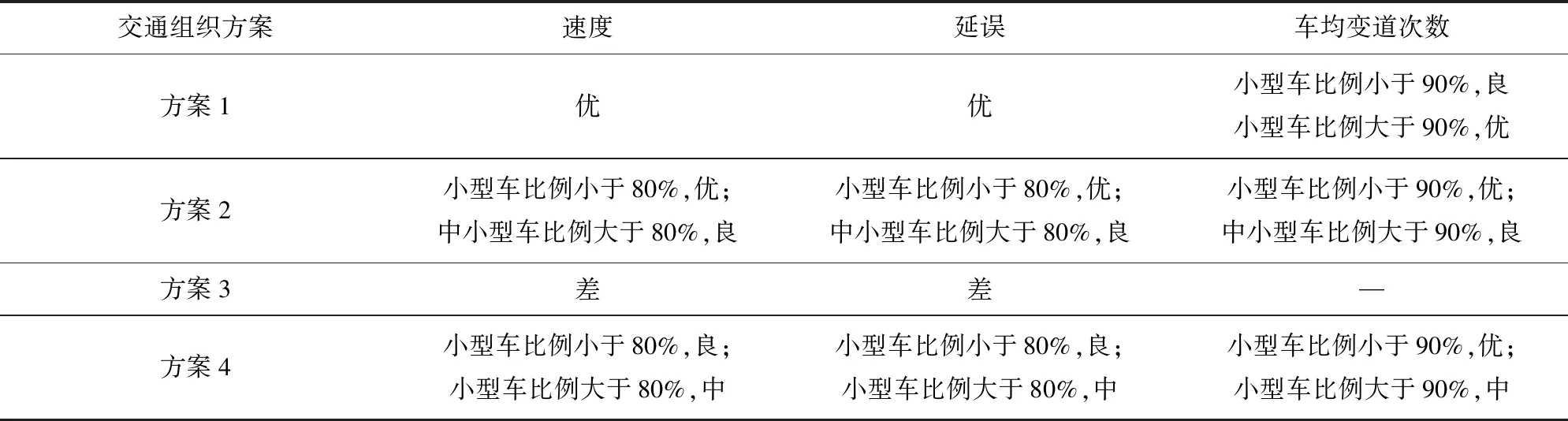
表2 不同交通组织方案特征指标对比

3 车道控制方案类比分析

3.1 仿真试验设计

结合特长隧道内交通组织方案，以及最小变道距离、安全变道成功概率的理论计算结果，将连接段与特长隧道作为整体设计了4种车道控制方案[12]，利用Vissim进行车道控制仿真试验[13].

方案1，隧道出口前后100 m禁止变道，小型车换道在洞内允许变道路段自行完成，连接段允许大型车由右向左单向变道.

方案2，隧道出口前后100 m禁止变道，连接段允许所有车型自由变道.

方案3，隧道内距出口前1.0 km至出口前100 m为定向变道路段，出口前1.0 km至出口前600 m允许由内侧向外侧变道，出口前600 m至出口前100 m允许由外侧向内侧变道.

方案4，隧道内距出口前1.0 km至出口前500 m允许外侧车向内侧变道，出口前500 m至出口前100 m允许由内侧车向外侧变道.

3.2 变道成功概率测算

在隧道-互通立交连接段长度受限的条件下，方案2允许在连接段自由变道，产生的交通冲突较多、通行效率低、安全性差. 如表3所示，方案1、方案3、方案4理论可变道长度基本一致，安全距离成功变道概率基本相同，在近期交通流量条件下按设计速度基本满足安全距离变道. 在远期交通流量条件下，按安全距离成功变道概率约为66%，在实际运行中可能造成部分车辆变道不满足安全距离条件或需要降低行驶速度[14].

3.3 车道控制方案比选

在Vissim数据基础上，选择每车平均延误(s)、车辆密度(pcu/km)、延误比、行车速度(km/h)等指标对车道控制方案进行类比分析. 不同车道控制方案下连接段每车平均延误如图6所示，在近中远期交通流量条件下，方案1每车平均延误无明显增长；方案2、方案3每车平均延误增长较大，在交通流量3 000～3 500 pcu/h时增幅达到200%以上；方案4涨幅介于方案1和方案2、方案3之间.

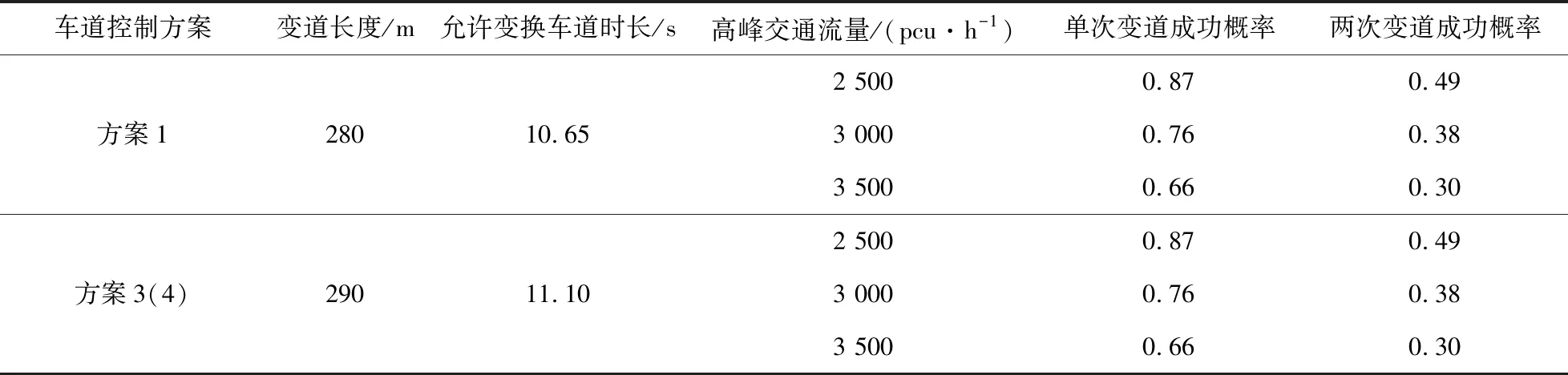
表3 变道成功率计算

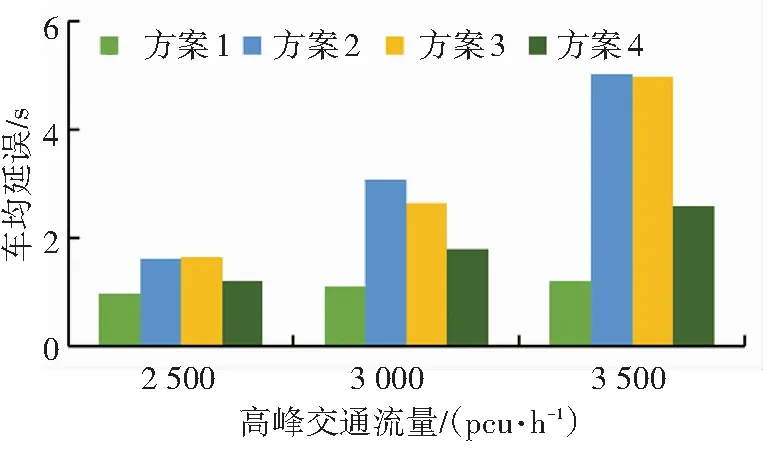
图6 连接段每车平均延误

不同车道控制方案下连接段延误比如图7所示，在近中远期交通流量条件下方案1延误比没有明显增长；方案2延误比增幅明显，在远期3 500 pcu/h交通流量下延误比为0.25，严重影响通行效率；方案3、方案4延误比存在一定增长，但优于方案2.

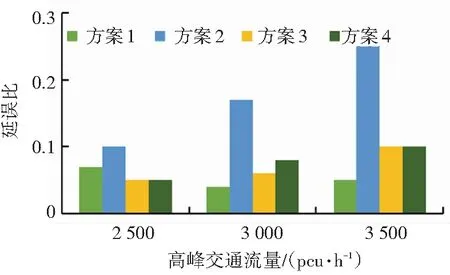
图7 连接段延误比

不同车道控制方案下连接段车辆密度如图8所示，方案2的车辆密度随着交通量增加急剧上升，在远期交通流量3 500 pcu/h条件下，车辆密度达到56.14 pcu/km，而其他3种方案车辆密度增幅较缓，在远期大交通流量条件下基本处于20 pcu/km.

不同车道控制方案下连接段平均速度如图9所示，除方案2在连接段自由变道的交通组织方案外，其他3种交通组织方案在近中远期预测的平均速度均存在小幅降低，但总体车速符合80 km/h的设计速度.

从变道成功概率来看，方案1、方案3、方案4在近中期交通流量条件下，按照设计速度行驶基本能满足按照安全距离变道. 在远期大交通流量条件下，按照安全距离变道成功概率降低明显. 鉴于特长隧道-互通立交连接段长度难以增长，在远期交通量条件下利用连接段变道成功概率会维持在一个比较低的水平[15]. 在交通流量增大时，宜采用方案3、方案4在特长隧道内完成车道变换，变道长度依据连接段变道成功概率计算确定.

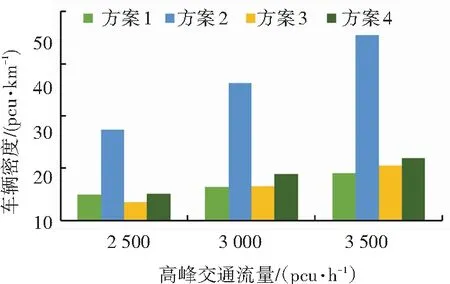
图8 连接段车辆密度

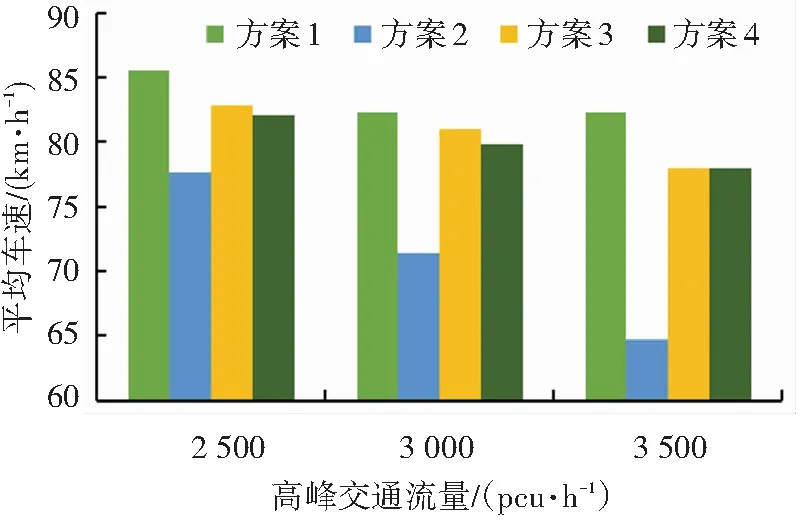
图9 连接段平均速度

4 结 论

1)毗邻互通立交的特长隧道交通组织方案设计时应进行连接段安全变道最小距离验算，并进行基于安全距离单次及两次变道成功概率测算. 在连接段长度不满足安全变道条件时，宜整体考虑特长隧道及连接段的交通组织方式，在隧道内完成驶出匝道车辆的车道变换需求.

2)在隧道线形条件较好、安全性指标较高时，多车道特长隧道宜采取内侧车道禁止大型车通行、外侧两条车道大小型车混合通行的交通组织方式，可以提高隧道运行安全性和通行效率最高.

3)综合考虑驾驶人行车需求、隧道交通事故分布特征等因素，示例特长隧道宜采取入口外200 m至入口内300 m、出口内外100 m禁止变道，隧道洞内基本段允许自由变道，距出口前1.0 km至出口前100 m的路段允许交替定向变道的交通组织方式.