深部高地应力环境下含白云母及石墨炭质板岩蠕变模型构建及其应用
2021-03-17谢云鹏陈秋南贺泳超陈正红田伟权周亚军黄小城李松
谢云鹏,陈秋南,贺泳超,陈正红,田伟权,周亚军,黄小城,李松
(1.湖南科技大学土木工程学院,湖南湘潭,411201;2.中铁十六局集团第三工程有限公司,浙江湖州,313000)
青藏铁路通车后,连接雪域高原的滇藏、川藏铁路成为世界关注热点。其中,高海拔地区的山岭隧道稳定性常受到围岩大变形影响,而滇藏铁路丽香段隧道受围岩大变形特征显著,炭质板岩段围岩的支护难题一直是西部地区高地应力隧道支护面临的重要挑战。为解决隧道围岩大变形的问题,国内外诸多学者[1−4]通过岩石蠕变模型及其损伤机理等方面进行研究、分析变形规律,进而优化围岩支护并控制变形。刘新喜等[5]通过对泥质粉砂岩进行分级增量加载三轴压缩蠕变试验,根据稳态蠕变速率与应力关系及给定蠕变速率阈值确定岩石长期强度。黄旻鹏等[6]对江西九江地区板岩进行单轴压缩蠕变试验,探究板岩各向异性对蠕变的影响,得出瞬时弹性应变随着层理面倾角变化规律。杨圣奇等[7]通过软岩流变中微裂纹的压闭和扩展研究,提出非线性损伤流变模型。谢云鹏等[8]对深埋隧道炭质板岩进行微观结构及单轴压缩试验,得到随含水率增大炭质板岩σ−ε曲线峰值后应力跌落减缓规律。宋勇军等[9]对炭质板岩试样进行单轴压缩蠕变试验,验证了Burgers 模型可反映炭质板岩的单轴蠕变特性。胡波等[10]通过单裂隙红砂岩压缩蠕变试验和PFC2D分析探究硬岩蠕变特性,结果表明只出现衰减和稳态蠕变变形。李松等[11]通过不同围压下室内炭质板岩加卸载三轴蠕变试验证明:当应力水平为抗压强度的60%~70%时,岩石仅出现衰减蠕变或等速蠕变,为抗压强度的80%时,发生加速蠕变。杨文东等[12]通过FLAC3D改进Burgers模型揭示了损伤参数对蠕变曲线的影响规律。刘圣等[13]通过三轴压缩下峰后蠕变试验分析了红砂岩峰后蠕变特征,得到了红砂岩峰后长期强度仅为其峰值强度的42.56%。FABRE等[14]对3种黏土含量较高的岩石进行蠕变试验,总结了其应变率与泥质含量的关系。GAO 等[15]采用Abaqus 对隧道中岩体进行等效锚固方法分析,分析了节理材料模型可用于模拟各向异性特征。TRZECIAK等[16]通过对波兰古生代页岩进行长期蠕变试验,改进Maxwell模型的适用性黏弹性本构模型。MANSOURI 等[17]通过对伊朗南部盐岩开展单轴压缩蠕变试验,得到轴向峰值应力−应变随弹性模量的增加而增大,蠕变量和蠕变率随轴向应力的增加而增大。
这些研究大多基于蠕变试验对弹黏塑性变形规律进行量化分析,对高地应力环境下富含白云母和石墨的炭质板岩蠕变特性及其蠕变模型构建的研究较少,尤其是结合应变损伤理论的适用蠕变模型及FLAC3D二次开发则更少。为此,本文作者针对高围压环境下富含白云母和石墨的炭质板岩蠕变特性展开研究,构建有针对性的蠕变模型,对新模型进行FLAC3D二次开发和验证,并将其应用于炭质板岩地层隧道围岩变形量的模拟,为解决深埋炭质板岩隧道大变形难题提供新理论和新技术参考。
1 工程概况
1.1 工程地质水文地质条件
丽江—香格里拉段铁路是滇藏铁路中的重要组成部分,地处青藏高原东南边缘的三江并流区。沿线岩溶发育、高地应力和突水涌水等不良地质条件复杂。其中某段隧道为Ⅱ级风险隧道,长度为9 527 m,最大埋深为1 155 m,属深埋隧道。隧区属剥蚀构造中高山深切河谷地貌,全线相对高差1 390 m,围岩岩体卸荷强烈,在施工中应对该隧道高地应力炭质板岩大变形区段高度重视。DK51+927—DK61+585 高地应力段炭质板岩分布如图1所示。
X射线衍射实验发现,富含碳质的层状板岩的原岩含有极完全解理的白云母(质量分数为17%)和具有润滑性的石墨(质量分数为3%),对炭质板岩的力学性能起到弱化作用。
1.2 围岩大变形情况
该隧道存在122 m大变形段出现边墙围岩侵限约20 cm、钢拱架出现麻花状扭曲变形(见图2),导致施工被迫中断。根据现场围岩变形监测数据显示,DK61+285断面拱顶沉降单日最大变形量达到41.5 mm,累计变形量达525.8 mm(图3);水平收敛单日最大变形量达到29.2 mm,累积变形量达264.6 mm。经现场地应力测试结果表明:深孔实测水平地应力最大值为38.84 MPa。
2 蠕变试验
2.1 试样制备及试验方案
针对高地应力环境下炭质板岩蠕变特性,开展室内三轴分级加载蠕变试验,试样取自隧道内原位大变形段。将所取岩样严格参照规范制成高×直径为100 mm×50 mm 标准试样,使用RYL−600三轴伺服流变仪,将岩石置于水中浸泡90 d 使其饱和,并对饱和试样进行不同围压的三轴分级加载蠕变试验。由常规力学试验得到饱和炭质板岩强度参数如表1所示。可见:当围压为0 MPa 和40 MPa 时,抗压强度分别为46.70 和159.05 MPa,这说明:围压增大对抗压强度影响显著。
根据地应力测试结果为38.84 MPa,设定三轴加载蠕变试验围压为40 MPa。试验加载方式为分级加载,根据常规力学试验测定炭质板岩三轴抗压强度,第一级轴向加压荷载为抗压强度的40%,随后每级加荷抗压强度10%并持续70 h 以上,直至最大荷载使岩石发生加速蠕变且试样被破坏为止。试验中水平围压以加载速率0.5 MPa/s 施加至设定最大围压,轴向荷载以加载速率100 N/s 加至预设值。
2.2 试验结果
围压为40 MPa 条件下炭质板岩试样分级加载全过程蠕变曲线如图4所示。由图4可以看出:试样在应力水平(σ1−σ3)处于较低状态时蠕变速率减小且未出现蠕变破坏现象;随应力水平增大到95.24 MPa,蠕变速率趋于稳定,进入稳定蠕变阶段;当应力水平增大到107.11 MPa 时,经历近10 h 的稳定蠕变后,岩石试样发生加速蠕变破坏。试样呈脆性断裂破坏,轴向与径向蠕变效应一致,但相较于轴向,径向的蠕变效应较弱。

图1 隧道纵断面图Fig.1 Profile diagram of tunnel

图2 初期支护变形破坏Fig.2 Initial support deformation and damage

图3 围岩监测曲线Fig.3 Surrounding rock monitoring curve

表1 饱和炭质板岩的强度参数Table 1 Strength parameters of saturated carbonaceous slate
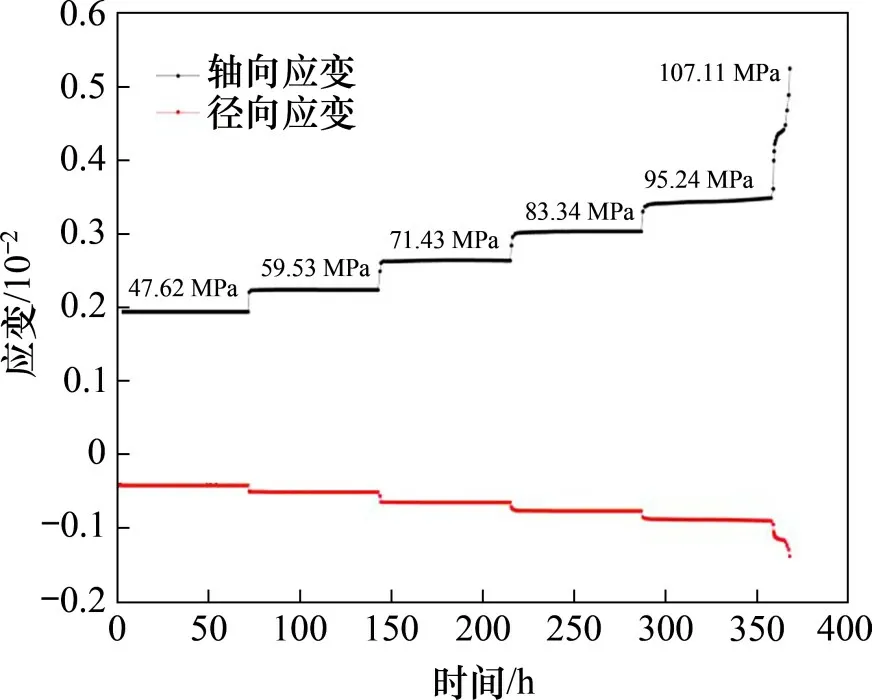
图4 全蠕变曲线Fig.4 Whole process creep curve
为分析不同应力水平下的蠕变特性,依照Boltzmann叠加原理将分级加载蠕变曲线拆分为不同应力水平下加载蠕变曲线(图5),并进一步绘制分级蠕变速率局部曲线(图6)。可见:当应力水平达到抗压强度σs的60%以上时才出现蠕变特性,故可认为存在蠕变应力阈值,在此应力阈值以下不发生蠕变;当应力水平达到σs的60%~75%时,主要呈现衰减蠕变,但蠕变速率较小,且衰减时间均在6 h 以内;当应力水平达到σs的75%~80%时,呈现加速蠕变,当轴向应变达到0.004时,发生蠕变破坏。因此,在高围压状态下,岩石加速蠕变直至破坏阶段是导致围岩破坏的主要原因。
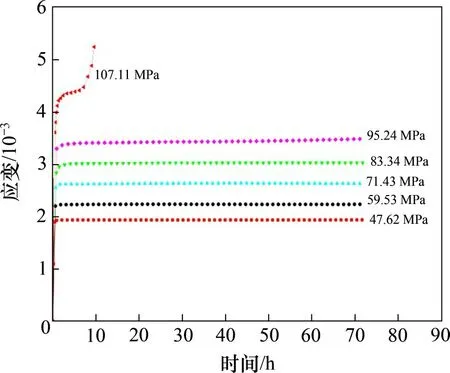
图5 分级蠕变曲线Fig.5 Graded creep curve
2.3 长期强度
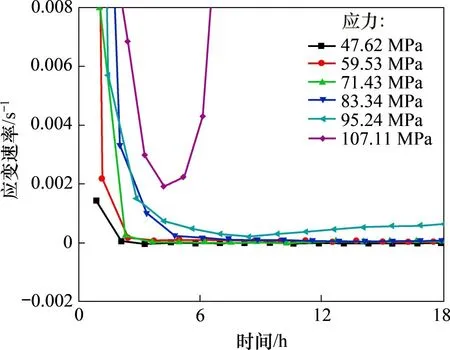
图6 分级加载蠕变速率局部曲线Fig.6 Local curve of graded load creep rate
将岩石长期强度作为评判岩石处于稳定和不稳定蠕变状态的临界值,对隧道工程设计有着重要的现实意义[18−19],故需要确定炭质板岩长期强度。本文通过室内分级加载蠕变试验,采用常用的等时曲线法间接确定炭质板岩长期强度。等时应力−应变曲线的拐点标志着岩石由黏弹性转为黏塑性阶段,岩石内部结构发生改变并开始破坏。恒定时间内所对应的蠕变与应力关系如图7所示。从图7可以看出,随轴向应力增大,等时应力应变曲线由线性曲线转为非线性曲线,且逐渐呈现放射状分散曲线,选定拐点出现在应力水平83.5 MPa处,故判定炭质板岩的长期强度约为123.5 MPa,为σs的76.8%。

图7 等时应力应变曲线Fig.7 Isochronic stress-strain curve
3 损伤蠕变模型
由等时应力−应变曲线可见,不同应力水平下炭质板岩蠕变呈非线性分布特征。在FLAC3D中常用的蠕变模型有Burgers 和CVISC 流变模型,Burgers 模型能较好地描述材料的衰减蠕变和等速蠕变行为,但是存在不能描述加速蠕变和不能响应塑性状态的缺陷;而CVISC 模型虽然能够响应材料的塑性状态,但不能描述应力状态小于屈服应力的加速蠕变变形。故基于CVISC 模型,根据硬化损伤理论引入损伤因子D,建立非线性硬化损伤蠕变模型HDCVISC (Harding Damage CVISC),以实现更准确描述炭质板岩加速蠕变特性。
3.1 硬化损伤理论
由分级加载蠕变试验发现,炭质板岩蠕变特性存在阈值即蠕变下限,在低应力水平时仅发生衰减蠕变,随应力水平增大出现等速蠕变,当应力水平增大到75%σs以上时,发生加速蠕变,此过程描述为炭质板岩随应力水平增大呈现先发生塑性硬化后进入损伤破坏阶段。故引入损伤体描述加速蠕变阶段,参照Kachanov 蠕变损伤律[20]可表示为
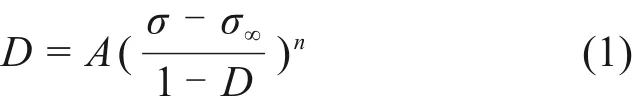
两边积分可得:
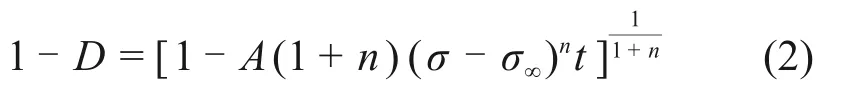
其中:D为损伤因子;A和n为材料性质常数;t为时间;σ∞为产生损伤蠕变的应力阈值,可以将其视为长期强度。理想状态下,由0时刻至蠕变破坏过程中,损伤因子D在0~1之间随时间t变化,如图8所示。
3.2 损伤蠕变模型变形与受力表达式
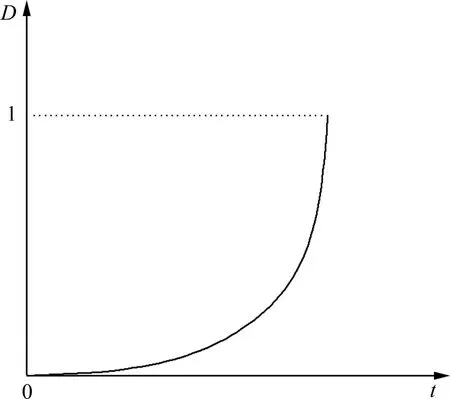
图8 损伤因子D随时间变化曲线Fig.8 Change of damage faction D with time
引入损伤因子的硬化损伤蠕变模型结构如图9所示,其中,σ为总应力;Ei为i部分弹性模量;σi为i部分模型所受应力,ηi为i部分黏滞系数;i=1,2,3,4,分别表示模型中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分。第Ⅰ部分为弹性体,用于描述蠕变应力阈值以下仅发生弹性应变阶段;第Ⅱ部分为硬化黏弹塑性,用村山体描述超过蠕变下限的稳定蠕变阶段;第Ⅲ部分为损伤蠕变,用损伤因子描述加速蠕变状态下岩石结构损伤蠕变阶段;第Ⅳ部分为塑性体,用于响应应力状态已超过岩石屈服面的塑性蠕应变阶段。
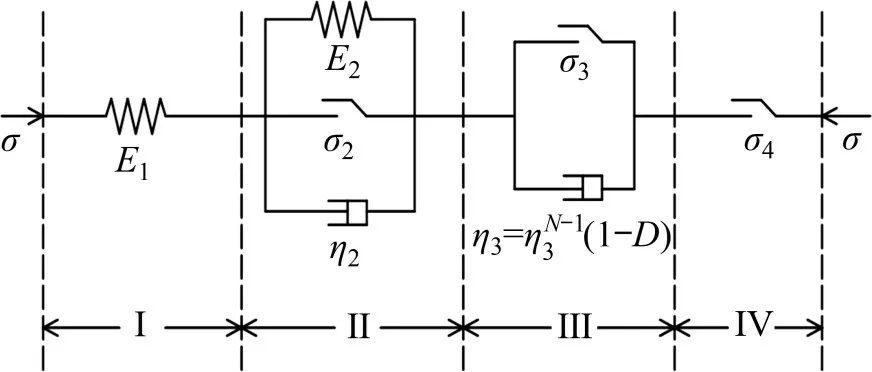
图9 HDCVISC模型结构Fig.9 Structure of HDCVISC model
基于FLAC3D软件中4 部分模型受力与变形公式,将模型变形速率代入变形差分形式中,得到对应模型随时间步长更新的新变形方程分别为:
新差分受力方程分别为:
弹性体:FN=E1Δu1+FN-1
其中:上标N和N−1分别表示当前时步和上一时步的迭代参量;ui为变形。
塑性体的受力与变形服从M-C 屈服准则和流动准则。村山体受力开关函数为

其中:Eiui为弹性体受力;Fs0为摩擦体受力。
由新差分受力方程得到硬化损伤模型在不同应力状态下变形方程表达式如下:
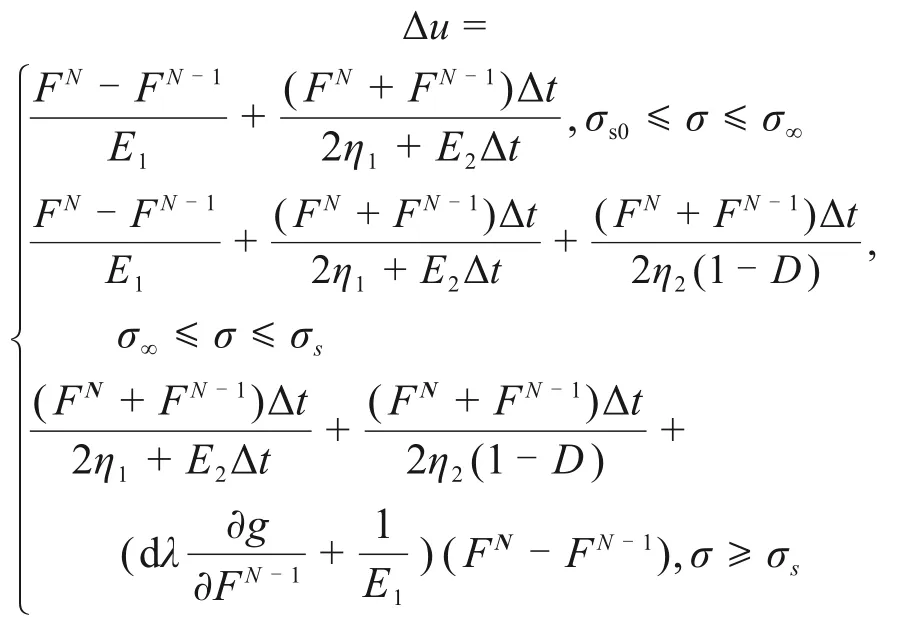
不同应力状态下受力表达式如下:

3.3 三维蠕变差分方程
对新建HDCVISC 模型进行了FLAC3D二次开发,为了便于该模型在程序运行的每一时步迭代程序化,推导了三维蠕变差分方程。
基于三维蠕变理论中的现有假设(即材料体积变形与时间无关;球应力不引起蠕变,偏应力才能产生蠕变;泊松比为常量),FLAC3D中所述蠕变本构模型是由偏应力−偏应变表达,球应变中不存在蠕变特性,且偏应变和球应变存在于弹塑性应变中[16]。
1)当σ≤σs0时,应力增量Δσij与应变增量Δεij分别为:

式中:下标ij表示应力面张量;K1和G1分别为弹性体的体积模量和剪切模量;S为偏应力;e为偏应变;δ为蠕变总伸长率。
偏应力S和偏应变e更新为:

式中:上标e表示硬化损伤模型中弹性体参量。
2)当σs0≤σ≤σ∞时,偏应力由村山体和弹性体构成:
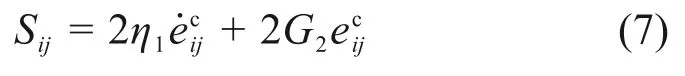
式中:上标c表示村山体参量。总应变率为

式(7)偏应力的增量形式为

村山体的应变更新为:
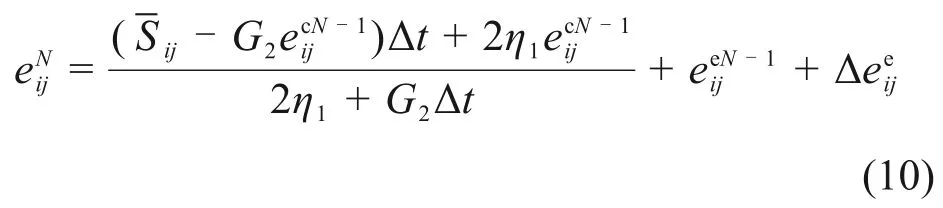
由式(9),偏应力更新为

球应力σm、应变εm在蠕变计算中相对独立,体积应变εvol的应力应变更新式为:

3)当σ∞≤σ≤σs时,由弹性体、村山体和损伤体应变率组成总应变率:

式中:上标s表示损伤体参量。
将总应变率两边积分,得到更新偏应变和更新偏应力分别为:

4)当σ≥σs时,总应变率为弹性体、村山体、损伤体和塑性体应变率之和:

式中:上标p表示塑性体参量。
塑性体偏应变在蠕变差分计算过程中相对独立,其偏应变更新式为

球应力只与球应变中的弹性应变相关:

其差分式和应力更新迭代式为:

总更新偏应变和偏应力为:

程序迭代时,应力应变更新式是运行计算的核心算式,蠕变数值模拟时每一时间步长将执行不同的应力应变更新式。
4 HDCVISC模型FLAC3D二次开发及验证
4.1 HDCVISC模型的开发
1)开发环境设置。将推导得到的硬化损伤蠕变三维差分方程、应力应变更新式,采用FLAC3D软件提供的本构模型二次开发程序接口,使用CPP语言在Visual Studio 2010 CPP 平台上对CVISC 模型源代码进行修改,模型命名为HDCVISC。在设定存放位置后,在Help示例文件、h文件名以及程序中模型名称中将出现ModelHDCVISC 的模型名称。
2)头文件编译。在HDCVISC.h 的头文件中可以对模型的预处理块自定义,包括开发编程过程中所需的私有变量名称、公共部分和基函数。定义私有变量时,HDCVISC 模型部分继续沿用CVISC 模型中的字符,包括体积模量bulk_、村山体剪切模量(以原Kshear_代替)、损伤体剪切模量(以原Mshear_代替)、村山体黏滞系数(以原Kviscosity_ 代替)、损伤体黏滞系数(以原Mviscosity_代替)、损伤变量包含的参数adamage_和ndamage_、M-C模型的强度参数等。
3)核心程序。新建HDCVISC 模型应力−应变张量与损伤变量随计算中每一时步更新将于Run()函数部分执行,程序执行流程如图10所示。二次开发的主要任务包括应力应变更新方程、损伤变量的更新和应力状态开关。程序编写完成后,将自定义本构模型代码编译成动态链接库文件,在FLAC3D软件中调用该文件即可应用自定义本构模型。
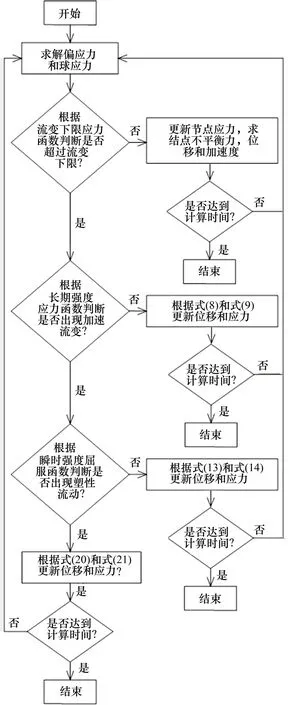
图10 程序流程图Fig.10 Program flow diagram
4.2 模型验证
将分级加载蠕变模拟试验所得蠕变曲线与室内试验结果进行对比,验证模型的一致性。在FLAC3D软件中参照室内试验中标准岩石试样尺寸建立模型,模型验证计算参数如表2所示。
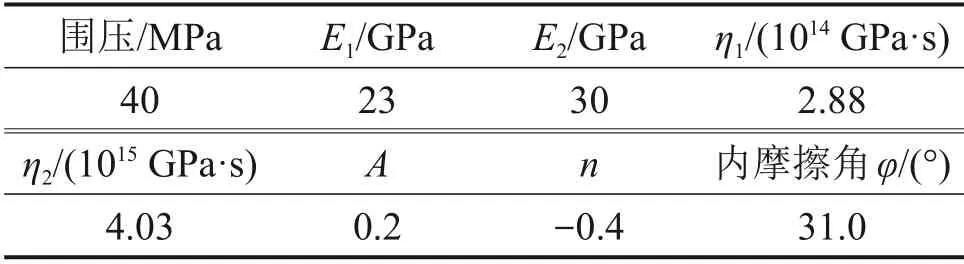
表2 模型验证计算参数Table 2 Model validation calculation parameters
模拟中施加固定约束于模型底部,此模型分为4 800个单元、5 061个节点(图11),计算中监测上顶面中心点的位移−时间曲线。
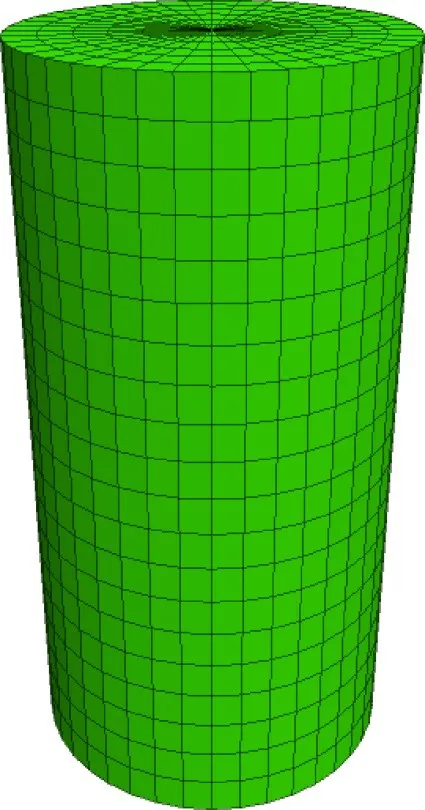
图11 HDCVISC模型网络Fig.11 Mesh of HDCVISC model
在数值模拟中,HDCVISC 模型通过history 命令,记录试验数据所监测到的岩石试样模型轴向应变和加速蠕变曲线,如图12和13所示。由于数值计算是单元计算迭代的过程,故模拟结果与室内试验的变化趋势以及轴向应变总应变存在一定差异,且数值模拟所得加速蠕变曲线的发展趋势较快,曲线斜率较大。
从图12和图13可以看出:新模型中模拟所得曲线与室内分级加载试验结果发展趋势基本一致;HDCVISC模型可以模拟岩石试样的蠕变特性(即衰减蠕变、蠕变下限以及加速蠕变的应力界限),基于该模型的模拟计算结果与现场岩石试样蠕变变形规律基本一致。
综合以上分析,基于CVISC 新建的硬化损伤蠕变模型可以正确反映出炭质板岩加速蠕变特性以及全蠕变曲线,表明该模型的二次开发是可行的,其内置的单元应力状态分析和参数独立赋值算法均可用于实际工程模拟分析。
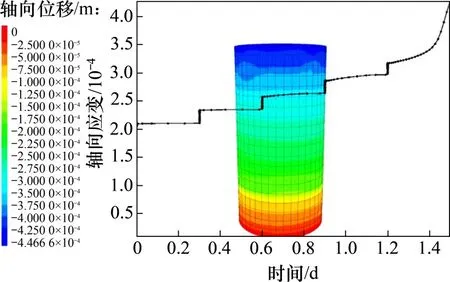
图12 分级加载轴向应变Fig.12 Axial displacement curves

图13 室内试验与数值模拟加速蠕变曲线对比Fig.13 Comparison of attenuation creep curves between laboratory test and numerical simulation
4.3 工程应用
在现场隧道施工中,按原支护方案施工出现了围岩持续大变形不可控难题[21]。在提出变更支护方案后,采用FLAC3D中新建HDCVISC 模型对变更设计方案模拟,将数值模拟所得围岩变形规律与现场实测围岩变形规律进行对比,验证新建模型的有效性。变更方案中衬砌支护参数如表3所示。
基于实际工况,采用上下台阶法模拟开挖—在隧道开挖模拟后及时施加初期支护—设置仰拱并施做二次衬砌的过程,并循环以上命令至隧道贯通。在模拟中,对拱顶沉降和上台阶左拱腰单边水平收敛位移进行监测,得到隧道围岩变形值,模拟结果如图14所示。可见:拱顶沉降和左拱腰单边水平收敛变形量均呈现前期以恒定变形速率增大,在施做二次衬砌后趋于稳定,与上台阶单边水平收敛变形相比,拱顶沉降速率更快、变形累积量更大。
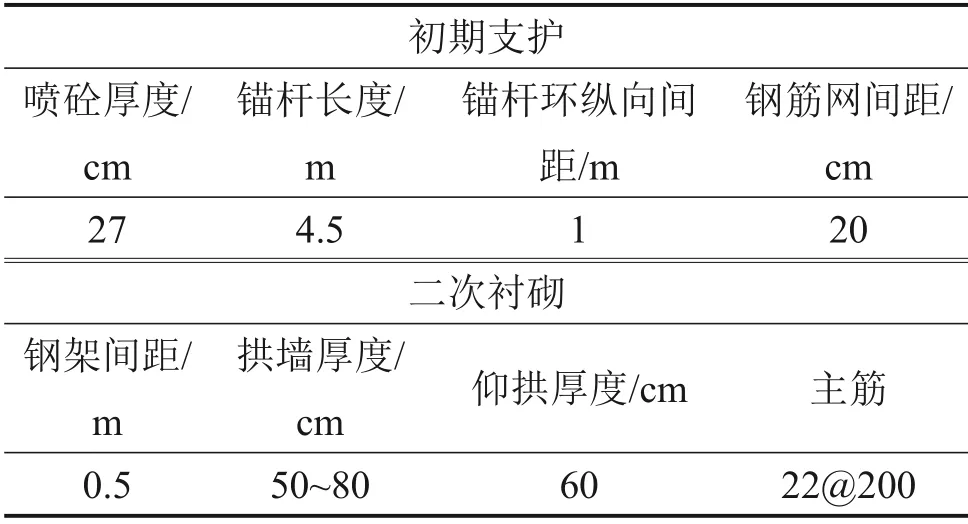
表3 变更方案中衬砌支护参数Table 3 Support parameters in modified program
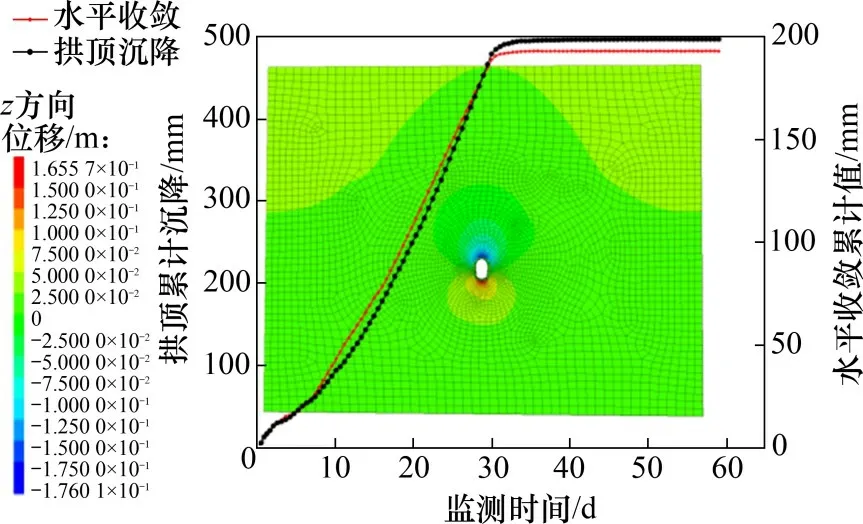
图14 二衬后拱顶沉降和水平位移模拟曲线Fig.14 After secondary lining simulated curves of vault settlement and horizontal displacement

图15 初期支护后模拟变形与实测变形曲线对比Fig.15 Comparison of simulated and measured deformation curve after initial support
模拟结果与现场实测围岩变形数据对比图15所示。可见:采用变更后衬砌方案,围岩拱顶沉降和水平位移均在施工期逐步趋于稳定,单边水平收敛进一步控制;拱顶沉降实测值比模拟结果偏大,相对误差为3.9%;单边水平收敛实测值比模拟结果偏小,相对误差为9.4%;模拟结果与现场实测结果一致,表明在开挖支护后28 d 围岩变形趋于稳定。在实际施工中,应在28 d 时进行二次衬砌。由此可得HDCVISC模型围岩变形模拟结果与高地应力环境下炭质板岩围岩现场实测变形数据发展趋势拟合较好,优化的模型能有效反映高地应力围岩变形特征,可为高地应力炭质板岩隧道设计和施工提供参考。
5 结论
1)通过室内分级加载蠕变试验,基于CVISC流变模型,结合硬化损伤理论,建立了40 MPa 围压条件下富含白云母和石墨的炭质板岩硬化损伤蠕变模型,推导出不同应力水平下变形与受力表达式。
2)基于新建蠕变模型结果,推导得到三维蠕变差分方程,进行HDCVISC 模型的FLAC3D二次开发,实现模拟计算中每时步的三维应力应变差分计算更新。二次开发流程及核心内容具有普遍性,可对同类岩石蠕变模型的FLAC3D二次开发提供参考。
3)将新模型所得蠕变曲线及工程实测围岩变形量与室内蠕变试验结果进行对比,验证了高地应力环境下富含白云母和石墨的炭质板岩硬化损伤蠕变模型及二次开发的正确性,说明程序是合理的。
