差序格局、社会网络与合作博弈研究

张 驰，岳中刚，王 飞

(1.南京邮电大学 经济学院，江苏 南京 210023 2.国家税务总局 税务干部进修学院科研所， 江苏 扬州 225007)

社会网络分析使用网络对社会结构进行研究，它通过节点以及连接对网络结构特征进行分析[1-2]。节点可以是人、社区、群体、组织、国家等，而连接则是节点之间的关系或信息交流，网络分析的焦点便是这些关系和交流反映出的现象或数据[3]。近年来，随着互联网的兴起，大量社交互动数据让社会网络分析所涉及的领域不再限于社会学，而是和经济学等其他领域交叉融合并发挥作用。

在社会网络中，网络的形成以及稳定依赖于某些特定节点的存在，这些节点多位于关键位置，起着促进网络连接和信息流通的功能，因此在网络中的地位也更加重要。图1展示了15世纪佛罗伦萨关键家族之间的通婚网络[4]，其中每条连接表示在两个家族成员之间存在婚姻关系。从图中可以看出，Medici家族在通婚网络中处于较中心地位，不同家族之间的连接路径多要经过Medici家族，如Barbadori家族与Albizzi家族。在这一时期，Medici家族通过联姻以及其他手段逐步加强和巩固了对佛罗伦萨商业和政治的控制，并提升了自己在经济关系和政治庇护网中的中心地位，为佛罗伦萨的后续兴盛奠定了基础。上例表明，对社会网络的运用有助于资源获得以及地位提升。因此，在社会网络中辨别节点的位置具有重要意义[5]。

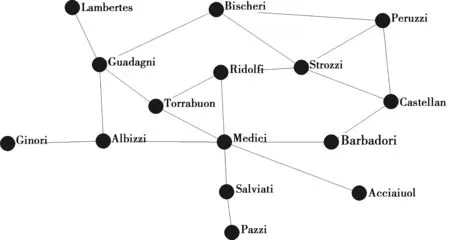
图1 15世纪佛罗伦萨婚姻网络

使用社会网络分析社会群体的优势在于将个体间的相互联系纳入考虑范畴，并考察节点在网络中所发挥的作用。节点在网络中的重要程度，可以从不同角度以及使用不同指标进行度量。现有社会网络分析研究中主要包含三类中心性度量指标[6]，分别是度中心性[7]、中介中心性[8]和紧密中心性[9]。但上述三类中心性度量都仅仅针对社会网络结构，即个体和个体之间是否存在联系，并未考虑其他可用信息。

基于以上问题，本文借鉴了“差序格局”部分思想，试图将新古典经济学的“理性人”[10]假设与“关系人”的分析相融合。“理性人”是在完全竞争条件下的“关系人”，“经济人”的有限理性不仅限于认知上的局限[11]，而且限于“关系人”之间关系强度的大小，关系强度受制于“关系人”的先赋差异，也就是“差序格局”中的位置和交往频率。通过“差序格局”，不仅可以理解“差”，即以个体为中心的向外扩散的社会圈，还可以通过研究“序”体现“差”。当前，学术界关于“差序格局”的研究多从社会学角度探讨其对社会结构[12-13]、心理认知[14-15]等的影响，或依靠调研数据提炼相关指标并代入模型进行回归分析[16-17]。相比较于上述研究，本文尝试从复杂网络角度刻画“差序格局”，通过借用费孝通“差序格局”理论思想，基于合作博弈理论分析社会网络中团体合作与分配问题并进一步刻画关键节点的特征，以期为社会网络研究做出理论上的贡献和实践上的指导。

一、模型构建

在网络经济学中，社会网络可以使用图G(N,E)表示，其中节点集N={1,2,…,n}代表了网络中的所有成员集合，而连接集E是一个n×n的实值矩阵，代表了成员之间所有联系的集合，gij表示i和j(可能是有权重和/或有向的)之间的联系。以15世纪佛罗伦萨婚姻网络为例，则节点集N的成员即网络中的所有家族，若给不同家族分别编号，则连接集E中所包含的gij则表示i家族和j家族的联姻状况，在此网络中，若存在联姻，令gij取1，反之则取0。E通常被称为邻接矩阵，因为它列出了那些彼此连接的节点。当E的各项取值大于2并且能够表示关系强度的情况下，则图为权重图；否则E的各项值只能取0或1，并且该图是无权重图，上例中婚姻网络即为无权重图。如果成员i和j之间存在联系，那么即认为gij∈E。如果对于所有的i和j，当gij≠gji时，则网络为有向的；而当gij=gji时，则网络为无向的。无向图的邻接矩阵为对称矩阵且gii=0，由于联姻为相互的，因此该婚姻网络是无向图。在本研究中，假定社会网络是无向图，即节点之间的关系是相互的。此外对于一个联盟(coalition)S⊆N，则子网络(subnetwork)Gs包括S中的所有成员以及它们在E之中的联系，即Gs=(S,Es)，其中Es={gij∈E|gij∈S}。在经济网络中，传统的中心性度量包括度中心性、中介中心性和紧密中心性，而不同的中心性指标分别从不同的角度对一个节点的重要性进行刻画。

度中心性通过节点的度来衡量它的中心性，如果单个个体在网络中认识的个体最多，那么它就是最重要的那个个体，因此一个节点的度中心性就是：

Cd(i)=d(i)/(n-1)

(1)

其中，d(i)代表节点i的度，也即和个体i直接相连的人数，n是网络中节点总数，可以看出0≤Cd(i)≤1，其中Cd(i)=0表示节点和其他所有节点均没有连接，为孤立节点，Cd(i)=1则表示节点与网络内剩余的所有节点均存在直接连接。在上例婚姻网络中，Medici家族与其他6个家族存在联姻关系，其度中心性位于首位，不过仅以微弱优势胜过Strozzi家族和Guadagni家族，为了更加准确地理解网络结构以把握Medici家族成功的关键，需要引入中介中心性指标。

中介中心性最早由Freeman[8]提出，是以一个节点在它所处路径上的位置有多优越为依据，考察节点如何促进了其他节点之间信息的流动。设Pi(kj)表示i所位于k和j之间的测地线(1)节点i和j之间的测地线代表这两个节点之间的最短路径，也就是说，不多于这两个节点之间的任何其他路径的连接个数的路径。(最短路径)的个数，设P(kj)是k和j之间的测地线总数，通过检查Pi(kj)/P(kj)可以估计出i在连接k和j中的重要性。将所有的节点对进行平均，则节点的中介中心性为：

(2)

对于Medici家族来说，其中介中心性指标值为0.522，说明在婚姻网络中所有不同家族之间的所有最短路径中，Medici家族位于它们中的一半以上，而具有高度中心性的Strozzi家族和Guadagni家族的中介中心性指标值分别为0.103和0.255。按照中介中心性的观点，Medici家族以婚姻关系作为交流信息、从事商业交易和获得政治决策的手段，比其他家族处于更佳的位置。

不同于中介中心性，紧密中心性度量了一个特定节点和任一其他节点的接近程度。Borgatti和Everett认为紧密中心性的本质是网络中信息流动的时间单位，而中介中心性则是网络中信息流动的频率[9]。节点的紧密中心性为：

Cc(i)=(n-1)/∑i≠jlij

(3)

其中，lij是i和j之间最短路径中连接的个数，同样，可以看出0≤Cc(i)≤1。

在现实的经济活动中，存在参与人通过网络转移资源、服务或其他可以相互影响的状态。例如，如果连接表示友情，则说明朋友之间可以通过交换而相互受益；如果连接代表商业合作，则指代产生货币支付行为。这些转移的模式决定了网络中每个参与人的最终盈利情况，能否盈利又取决于网络结构、网络中各参与人的位置、网络参与人的生产价值，以及参与人讨价还价能力等各方面。而分配法则根据网络参与人的背景细节对其最终盈利情况进行预测。

合作博弈论以所有参与人的社会为起点，提供了一个社会中创造的总价值在它的成员之间分割的预测。它把参与人的每个可能子集将要创造的相对价值考虑进来，当参与人在如何分配社会创造的总价值上讨价还价时，把参与人不同联盟的价值考虑进来，则所产生的分配可以解释为对结果的预测。

根据以上内容，做出如下设定：在合作博弈中，存在(N,v)，其中N代表着有限的参与人；v是一个函数，负责为每个联盟S⊆N分配价值v(S)，代表了联盟对总体社会价值的负责或贡献程度。另外，规定v(∅)=0。那么对于所有的参与者，分析的核心就是社会价值如何在成员之间分配。衡量一个参与者对整个网络的负责或贡献程度将通过一种归责(2)归责(imputation)是指一个函数φ:W(N)→n，使得∑iφi(w)=w(N)。实现，而夏普利值作为一个著名的归责法，通过衡量参与者对每一个它所参加的联盟的边际贡献分配v值[18]。夏普利值计算公式如下：

(4)

其中，n为参与人总数，联盟S不包括参与人i，(式)4的含义是：假设联盟每次只吸收一个参与人，每一个参与人都要求w(S∪{i})-w(S)作为其对联盟贡献的合理补偿，参与顺序的不同会产生不同的贡献值，每一个顺序出现的概率是(#S!(n-#S-1)!/n!)，而贡献值在这所有顺序上的平均值即为夏普利值。

本文受“差序格局”启发，该词由费孝通先生提出，旨在描述亲疏远近的人际格局，如同水面上泛开的涟晕一般，由自己延伸开去，一圈一圈，按离自己距离的远近来划分亲疏[19]。根据“差序格局”，人之间的关系是由血缘、地缘、经济地位、政治地位和知识文化水平决定的[20- 21]，由血缘、社会和法律关系不同构成人之间不同的关系。不同的关系产生不同的等级，而有赖于等级的不同，中国文化中的尊卑上下、长幼有序得以存续，进而影响着中国社会的资源配置、奖惩机制、社会流动乃至文化制度[22]。可以看出，“差序格局”较为精准地解释了中国的社会结构，研究“差序格局”，不仅能够了解社会如何组成，也可以帮助理解作为社会成员的个体的人格是怎样形成的[23]。因此，人在不同人面前或者不同人群中表现出的理性程度并不相同，因为关系的亲疏而改变，即每人面对相同事情时，因为关联事情的人或人群不同，行为方式也将不同。假设一个人拥有多个关系圈，关系越紧密其行为之间效用越大，按照“差序格局”的逻辑，亲缘关系形成的效用最大，以后依次递减。当然，此类效用可取决于其他因素，如距离与交往频率，中国人认为“远亲不如近邻”便是交往频率可以提高彼此关系强度的现实概括。

鉴于此，本研究根据假设建立模型：个体之间关系程度取决于两个变量，其一，关系强度R={kij}kij∈E,kij≥0(如亲人、朋友、同学和同事等)；其二，节点的个人禀赋I={wi}i∈N,wi≥0(如血缘、身份和特殊技能等)，因此，对于个体i，其与个体j的关系程度可表示为：

eij=wi*kij

(5)

通过式(5)可以看出，个体交往是通过关系，不同强度的关系对于“关系人”之间的影响并不一样，某一个“关系人”的关系总程度是其与所有相关联个体的关系程度加总，因此有：

(6)

但当个人的关系程度扩展到联盟的关系程度时，式(6)对于联盟的关系程度的描述缺乏解释力，对不同节点的关系程度的单纯加总也会导致重复计算问题，因此，为了衡量联盟的关系程度，引入以下定义：

当S⊆N时，如果Gs是连通(3)连通网络，是指如果网络中的每两个节点是通过网络中的某一条路径相连通的，否则，称为不连通网络。的，则称S为一个连通联盟，否则S则为不连通。对于一个连通联盟S，有定义：

(7)

其中，g是关于S,I,R的非负函数，用以衡量网络中联盟的关系程度，能够反映当前所具有的信息和所处的状态。当联盟S不连通时，有定义：

σ(S)=maxT⊂S,T连通σ(T)

(8)

从式(8)可以发现，对于每一个不连通的联盟，其σ值取决于这个联盟中关系程度最强的连通部分。为了通过节点的“差”反映节点的“序”，有定义：

(9)

通过式(9)，可以判断出网络中重要节点及其连接，为后期的收益分配提供理论依据。当网络中某一节点自身能力得到提升或它和其他节点的联系强度加深时，其在整个网络中的重要性都可获得提高，在式(6)中可通过调整权重来实现这一点。

随后，基于I,R对网络G=(N,E)进行合作博弈下收益分配度量：

Cm(i)=vi(σ)

(10)

其中，vi(σ)是个体i在网络G中的夏普利值，即个人所获得对应收益。而所有成员相对应的“序”都将通过Cm值的大小进行排列，从而发现网络中关键节点。Cm的计算通过下例说明。

假设存在网络G=(N,E)，如图2所示，网络G包括5个节点，分别用A，B，C，D，E表示，以及6条连接，分别代表各节点之间的相互关系。假设节点E由于之前的某种行为提升了自己的个人强度，而其他节点的个人强度保持不变，那么在评估E点在网络之中的重要性时需要将这一点考虑进去，此处令E点的个人禀赋wE=3，而其余各点的个人禀赋均为1。此外，假设观察到节点A和B之间的信息交流强度或频率要高于其他成员，因此，为A,B之间的关系强度赋予权重kAB=2，而其他连接为1，具体详情见图3。

图2 社会网络G=(N,E)

图3 赋予个人强度和关系强度的社会网络G′=(N′, E′)

根据之前的定义，可以计算出每一个联盟的σ值。表1提供了32个联盟所分别对应的σ值，而每个成员的中心性度量指标Cm在表2中显示，对应的排名顺序为：D，A，B，E，C。可以看出，A，B之间更频繁的信息交流为他们带来了更加靠前的位置，表示其在网络中有着较高的重要性。而D与网络中其他4个点均有联系，因此成了网络中排名第一的节点。E虽然身处网络边缘，但由于其自身所具有的个人强度要大于其他4个点，因此在网络中的重要性要高于C。

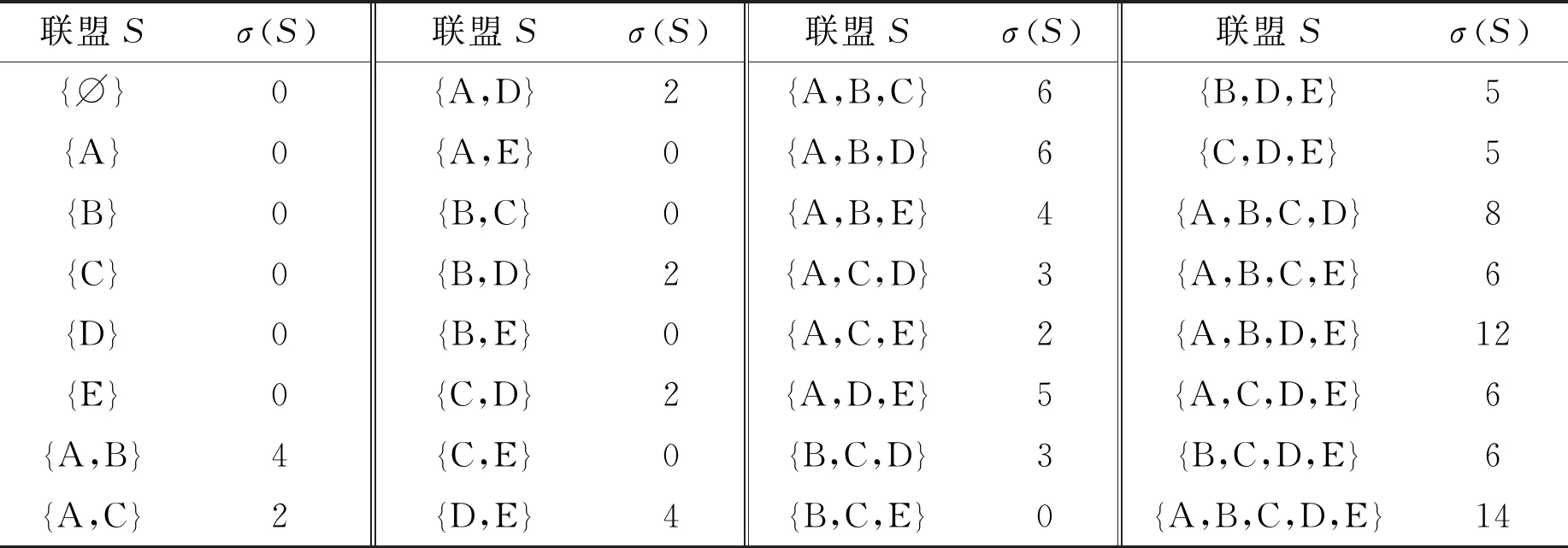
表1 网络G′中各联盟σ值

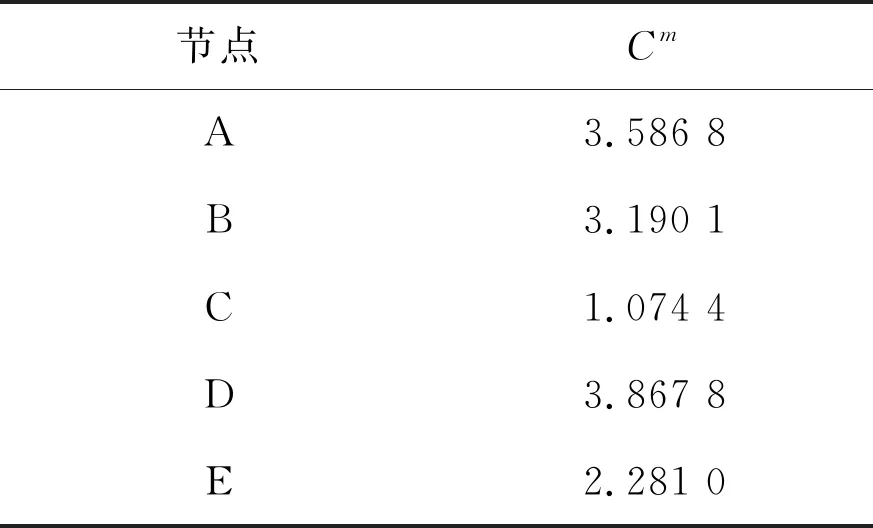
表2 网络G′中各节点合作博弈收益值Cm

二、 仿真分析

虽然东西方文化中关系的内涵不同，如在英文文献中关系(relationship) 也可以用拼音Guanxi来代替[24-25]，相比较于西方，东方对待关系的态度也不尽相同，但不可否认的是，无论在东方的“差序格局”中还是在西方的“团体格局”中，网络中的关系都是维系网络存在的重要纽带。一方面，关系作为纽带维系一个网络的存在时，可以通过相互的连接施加影响，从而推进整个网络的发展，这是关系的优点；另一方面，关系的滥用也有可能会毁掉整个网络，如企业中的裙带关系等。为了模拟社会网络中收益分配的情形，使用Matlab软件仿真构建了一个连通的社会关系网络H(见图4)，并使用UCINET软件予以展示，网络中的节点通过直接或间接的方式相互连接。现实生活中的微观、中观、宏观网络中的重要节点定位皆可以使用此种方式进行描绘并求解。

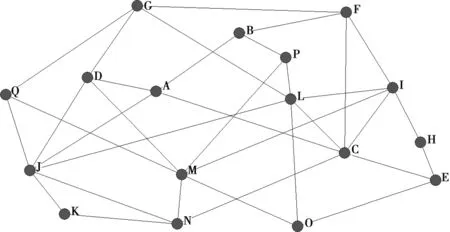
图4 模拟社会网络H

在网络中，需要为不同节点赋予个人禀赋，此处假定1，2，3，4四种禀赋值，取值越大，代表节点自身能力越强。节点个人禀赋的赋予可以采用如下方法：首先假定所有节点的个人禀赋为1，然后对于存在上下级关系的节点，即如果A为B的上级，B为C的上级，则A,B,C的个人禀赋分别赋值为3，2，1。在其他存在亲属、朋友、同学、合作伙伴等关系的网络中，视情况为其赋值。本文中所有节点个人禀赋I={wi}i∈N，见表3。此外，在现实中，节点之间的沟通强度或频率，即关系强度无法为外界准确得知，且此处为计算简便，假设所有节点之间的关系强度R={kij=1}ij∈E。在实际应用中，可以根据对历史数据的整理和总结更加准确地为I和R赋值。为了检查此次赋值的效果，后续会对使用I和R得到的排序进行灵敏度分析。

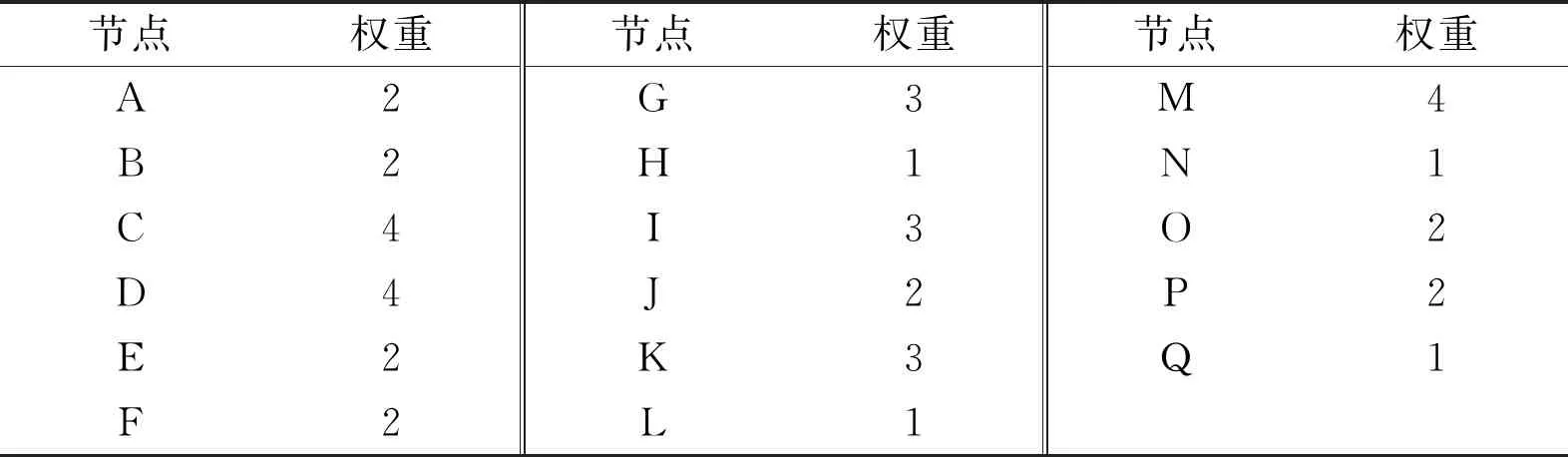
表3 模拟社会网络H中节点禀赋

首先需要根据模型构建节点排序序列，使用式(7)中的g(S,I,R)函数，根据其合作博弈收益Cm将节点降序排列在表4的2，7列中，而其在网络中的重要程度也可以通过第1列所对应的排名体现。通过与其余列的度中心性、中介中心性和紧密中心性相互比较可以发现，传统的中心性度量仅仅将网络结构考虑在内，而忽略了节点本身携带的额外信息。此外，传统的中心性度量方式不可避免地会产生多个节点中心性值相同的情况(表中每列节点上标星数目相同即代表中心性值相同)，当相同值较多时，无法更加准确地分辨节点的重要性，也导致了在社会网络分析中，无法确认最重要的一部分节点。例如，假设这是消费者之间的协同消费网络，则意味着平台需要花费大量人力物力对整个网络的消费者实现数据追踪，这对大型企业当然不会构成问题，但是当企业规模较小，无法承担起整个网络的追踪成本时，将有限的资源集中到主要的个人身上，可以帮助企业节约资金、提高效率。在现实中，无论社会关系网络是何种类型，其存在以及维系是依赖于部分节点的，而由于对全局的观察受到较多因素限制，因此，只针对部分节点，即表4每列的前5位进行分析。

在表4中，可以发现，无论采用哪一种计算方式，M，C，I都占据前5名的位置，这说明此方法相对于传统的中心性度量方法，不仅考虑了网络的结构，也考虑了节点的个人强度，而且根据合作博弈中心性进行排序的最终结果也是唯一的。

表4 模拟社会网络H中节点中心性排序

对合作博弈收益的排序进行灵敏度分析需要对比不同的排列。例如，假设网络H中的连接并未全部被观察到，导致遗漏了4条连接，只能观测到网络H′(见图5)，此网络中所有节点合作博弈收益的降序排列见表5的第二列Cn。为了对比方便，第一列为Cm。Cm和Cn的差异通过ρ(Cm,Cn)予以计算，其方法如下：

图5 移除4条连接后的模拟社会网络H′

表5 模拟社会网络H和H′中节点合作博弈收益排序

首先，在Cm排序表内，每一个节点根据自己的位置被赋予相应的权重，见表6。随后计算离开Cm前5名位置节点和进入Cn前5名位置节点所对应的权重的加总，这种权重赋予方式会导致：当Cm内排名前5名的节点离开它的位置，而较低排名的节点进入Cn前5名位置时，会产生较大的ρ值。在本研究例子中，ρ值最大的情形出现在Cn的前5名由Cm的最后5位组成，则ρ的最大值为1+4/5+3/5+2/5+1/5+8/12+9/12+10/12+11/12+1=(15/5)+(50/12)=7.17。当两列并没有显著差异时，ρ的值较小(并接近于0)。通过对比网络H和H′，可得ρ(Cm,Cn)=1/5+1/12=0.28。可以看出对于网络的微小变动，此方法的结果依旧保持稳健。

表6 模拟社会网络H中各位置赋予权重

三、结 论

本研究受“差序格局”启发，结合网络理论与博弈理论，为识别社会网络中的重要节点提出了一种新的定量方法——合作博弈收益，即对社会网络中的“差”异进行排“序”。此方法结合了社会网络分析与合作博弈论中的夏普利值归责法，其优势在于不仅将网络特征纳入考虑，也吸收了非网络特征，如节点的能力、社会地位，以及和其他节点的关系强度等。和度中心性、中介中心性和紧密中心性相比，合作博弈收益能够更加准确地对节点的重要性做出区分，在传统三种中心性无法对部分节点的重要性做出判断时，合作博弈收益通过衡量网络连通性、节点强度和关系强度对重要性做出了更加准确的判断。为了验证这一点，采用了灵敏度分析，结果表明，相对于网络中的微小变动，合作博弈收益的分析结果仍能保持稳健。

合作博弈收益能够充分考虑网络结构之外的信息，它在度量节点重要性方面相对于传统的中心性指标具有显著的优势，这为现实生活中的社会网络分析提供了新的视角。通过对信息的深层挖掘，合作博弈收益也能为社会网络分析提供更多有价值的见解。因此，在未来的研究中，此类方法可适用于多个领域，如协同消费网络，使用此方法可以帮助相关企业或组织更好地进行收益分配或成本分担，进一步地，通过挖掘和使用关键节点的有效信息，从而达到提升效率以及改善福利的目的。随着通信技术的加强，现实中个人、组织间网络的形成也愈发便利，通过对大数据进行分析，可以收集大量社会网络结构以外的信息，这些信息有利于为节点和连接赋予适当的禀赋和权重。然而在现实环境下，社会网络并非一成不变，而是处于一种动态演化状态下，那么，网络的动态演化，新旧节点的消失、加入，新旧关系的消逝、产生又会对合作博弈收益分配结果产生何种影响？笔者会在将来的研究中继续深入探讨。