考虑对近邻管线影响的隧道洞口段施工爆破药量优化研究

韦建昌　潘峰　王潮鑫

摘要：山岭隧道洞口段存在燃气管道时，根据设计和相关规范的要求，必须要对管道附近的振动速度进行控制。文章以实际隧道工程建设为背景，基于萨道夫斯基经验公式设计了三种装药方案，并通过数值模拟分析了管道对三种方案爆破的动力响应。研究结果表明，增加爆破中的起爆段位能够减小爆破振动速度，在相同段位下优化辅助眼各段的炮孔数量和装药参数能够大为降低爆破振动速度，从而达到规范和设计的振动速度控制要求;基于萨道夫斯基经验公式计算的药量能得到一个初步的装药量，通过数值模拟能够进一步优化装药量，使振动速度满足规范和设计要求;当隧道洞口附近存在建筑物或者构筑物时，应尽量增加二者之间的最小空间距离。

关键词：爆破工程;减震技术;数值模拟;方案优化

中国分类号：U445.53文章标识码：A381464

0 引言

山岭隧道建设大多使用钻爆法施工，爆破振动势必会对周围建筑物或构筑物造成影响[1-4]。爆破振动影响的表征参数主要为峰值速度[5]，而爆破振动特征的影响因素有很多，如爆孔的布置及特征、药量药性的选择、抵抗线的确定等[6-8]。其中爆破方式对其振动效应的影响是十分显著的[9]，故对爆破方式的优化是极具研究价值的。学者们通过理论分析、数值模拟和现场实测等方式研究了爆破振动时结构的响应速度和应力，通过爆破药量与实际药量进行对比优化及运用现场监控量测优化爆破药量等手段，使得隧道爆破所产生的影响在规范规定的范围之内[10-12]。学者们分析了爆破对洞口的边仰坡影响、最大起爆药量安全阈值及高边坡的动力响应[13-15]。故本文为了得到洞口段爆破施工对近邻管道的最佳施工方案，以实际隧道为工程依托，基于三维有限元计算软件分析不同爆破段数、不同炮孔数量、不同单孔装药量条件下不同距离的三个测点的震动速度，以期得到最优方案。

1 工程概况

某隧道在设计时因条件限制，始终无法大距离避开一条燃气管道。在平面设计图上该隧道与燃气管道相距约24～240 m，现场实测表明该隧道出口段距离天然气管道最近水平距离是35.68 m。该隧道出口方向洞口仰拱的最低高程高于天然气管道高程，竖向高差约为18.2 m。该隧道为山岭隧道，采用钻爆法施工。根据设计要求，与燃气管道相距150 m范围内隧道采用冷开挖，当两者距离在150～250 m时采用控制爆破，根据规范的规定要求，爆破振动速度必须控制在2 cm/s以内。

2 基于萨道夫斯基经验公式的爆破药量设计

为了保障出口段距洞门150～250 m采用控制爆破时，燃气管道处的爆破振速能满足设计和规范要求，必须对爆破装药参数进行优化。隧道工程实践中，爆破参数确定常用萨道夫斯基经验公式，见式（1）。岩土体参数K、α、爆心距和最大振动速度均已知，根据萨道夫斯基经验公式即可求出装药量。

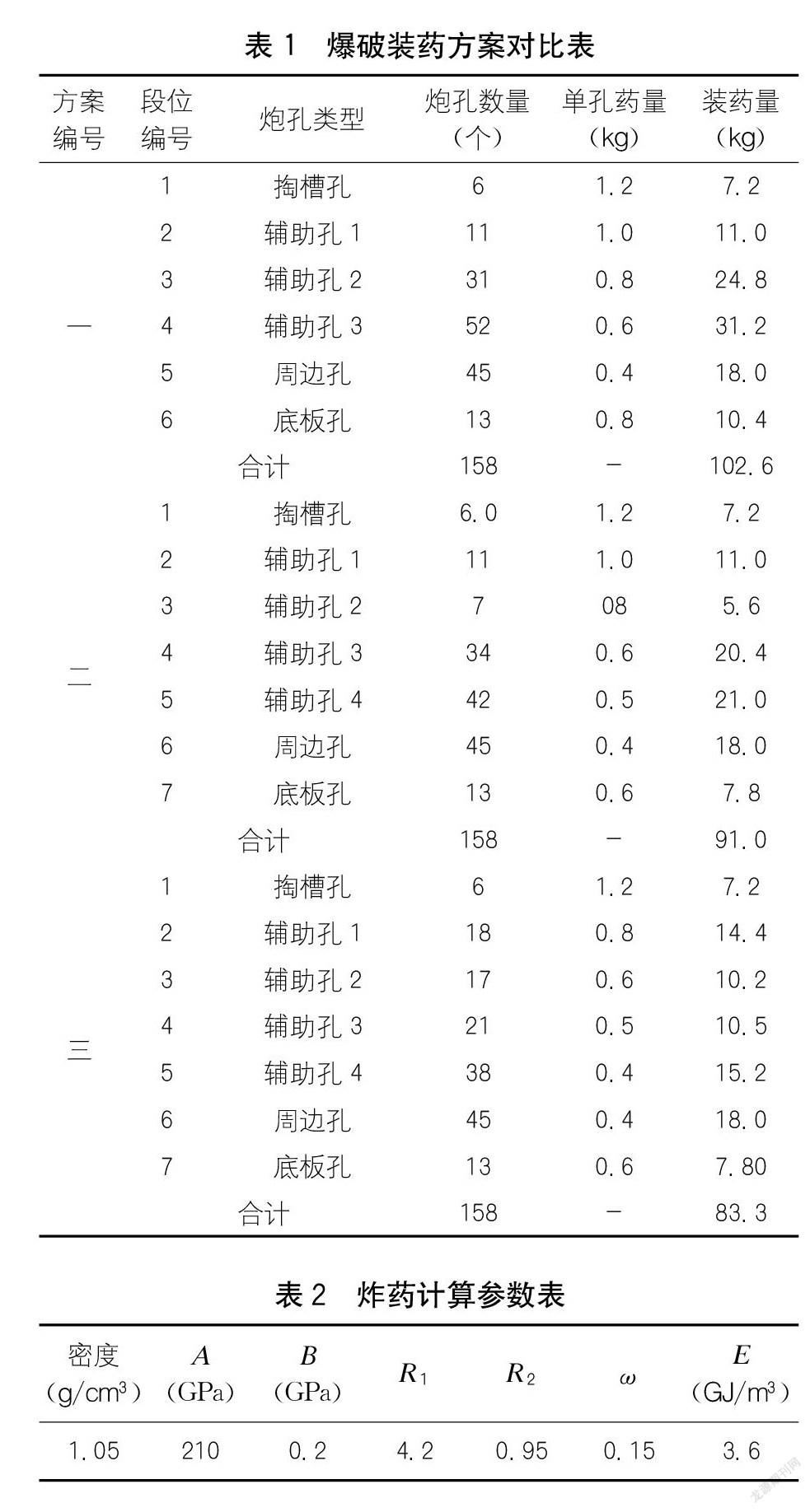
隧道出口洞段开挖的方法为台阶法。根据工程地质情况、实践经验与萨道夫斯基经验公式，本文在出口方向洞口段提出了三种不同的装药方案。三种爆破方案的炮孔数量均为158个;方案一的起爆段数为6段，其余两个方案的段数均为7段;方案一的总装药量为102.6 kg，方案二的总装药量为91.0 kg，方案三的总装药量为83.3 kg。不同方案的各段位炮孔数量及单孔装药量见表1。

3 理论依据及参数拟定

3.1 计算假定与状态方程

数值计算采用了以下假设：

（1）岩土体为理想弹塑性介质;

（2）考虑岩土体变形的时间效应;

（3）岩土体为各向同性均匀介质;

（4）模型无反射边界条件。

高能炸药起爆以后，常用JWL（Jones-Wilkens-Lee）状态方程，见式（2），求得炸药爆炸内部单元所受压力P。JWL状态方程描述了高能炸药爆炸时化学能的变化情况：

3.2 计算参数

根据该工程勘察设计资料，爆破施工拟采用2号岩石硝铵炸药。本数值模拟采用2号岩石硝铵炸药的密度为1.05～1.25 g/cm3，爆炸力度為295 mL，炸药猛度为12 mm，爆炸速度为3 250 m/s，其计算参数如表2所示。

数值模拟使用有限元ANSYS/LS-DYNA软件，数值模型中的岩土体、C30混凝土采用塑性模型，模型定义方式为*MAT_PLASTIC _KINE MATIC。岩土体与混凝土的计算材料参数如下页表3所示。

3.3 数值模型

数值计算采用三维计算模型，模型尺寸为：X方向上宽度为175 m，Y方向上最大高度为148 m，Z方向上最大长度为177.3 m，模型顶面以实际地形建模。计算模型中四周边界约束水平位移以模拟场地的半无限元边界，底面边界约束沿竖直方向位移。有限元计算模型共有740 276个体单元、138 392个节点。有限元模型如图1所示。

在燃气管道线路位置上共布置3个监测点（见图1），分别在距右线隧道洞口最短空间直线距离为83.68 m处布置一个监测点，距右线隧道洞口100 m处左右各布置一个监测点。通过监测爆破过程中各测点振速，以设计和规范的临界振速优化装药参数。

4 计算结果分析

本文通过数值模拟了三种装药方案，分析布置的三个测点振动速度在不同装药方案条件下的变化规律，详述如下。

（1）方案一计算结果

方案一计算结果表明（见图2），测点2的X方向振速最大，为1.66 cm/s，比测点1处X方向振速大69.3%，比测点3处X方向振速大40.6%;Y方向振速最大值也在测点2处，为1.51 cm/s，比测点1处Y方向振速大23.7%，比测点3处Y方向振速大34.8%;Z方向振速最大值也在测点2处，为2.32 cm/s，比测点1处Z方向振速大34.1%，比测点3处Z方向振速大31.1%。测点1和测点3的距离相差不大，所以两者各个方向的振速大小都相差不大。因为测点2距离天然管道的距离最近，所以测点2的振速最大，

其在Z方向的振速最大，比在X方向的振速大39.8%，比在Y方向的振速大53.6%。离爆破点的距离越近，响应振速越大，各振速分量中Z方向振速最大。测点2的Z方向振速>2 cm/s，不满足设计和规范要求。

（2）方案二计算结果

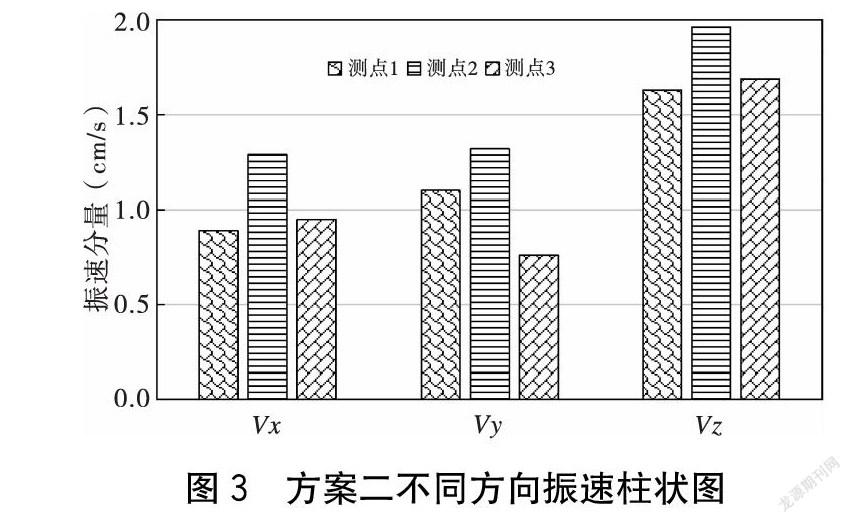
方案二计算结果表明（见图3），测点2的X方向振速最大，为1.29 cm/s，比测点1处X方向振速大44.9%，比测点3处X方向振速大35.7%;Y方向振速最大值也在测点2处，为1.32 cm/s，比测点1处Y方向振速大20%，比测点3处Y方向振速大73.6%;Z方向振速最大值也在测点2处，为1.96 cm/s，比测点1处Z方向振速大20.2%，比测点3处Z方向振速大15.9%。测点2的Z方向上的振速最大，比在X方向上的振速大51.9%，比在Y方向上的振速大48.4%，相比于方案一的Z方向振速降低了24%，故爆破段数增加能有效降低爆破振动对管道的影响，三个测点各方向的振速都<2 cm/s，满足设计和规范要求。

（3）方案三计算结果

方案三计算结果表明（见图4），测点3处X方向振速最大，为0.89 cm/s，比测点1处X方向振速大50.8%，比测点2处X方向振速大11.2%;Y方向振速最大值在测点2处，为1.3 cm/s，比测点1处Y方向振速大94%，比测点3处Y方向振速大125%;Z方向振速最大值也在测点2处，为1.58 cm/s，比测点1处Z方向振速大125%，比测点3处Z方向振速大90.3%。

各测点振速分布规律与方案一、二不同，X方向上振速最大的不是测点2而是测点3处。由此可知，在起爆段位相同的情况下，调整各段位炮孔数量和装药系数能够进一步降低爆破对周围建筑物和构筑物振动的影响。

（4）不同方案各测点振动合速度

由图5可知，方案一振动合速度最大值在测点2处，为2.55 cm/s，比测点1大18%，比测点3大17.7%;方案二振动合速度最大值也在测点2处，为2.24 cm/s，比测点1大19.1%，比测点3大16%;方案三振动合速度最大值也在测点2处，为1.71 cm/s，比测点1大10.3%，比测点3大11.2%。方案一振动合速度最大值比方案二大13.8%，比方案三大86%。三个方案中测点2的最小振动合速度为1.71 cm/s，与其他两个测点的振动速度仅相差10%左右，因此方案三比较合理。

5 结语

（1）当管线与隧道洞口的空间距离从83.68 m到100 m时，振动合速度至少减小10%。距离起爆位置的空间距离越短，爆破产生的振动速度越大。当隧道洞口附近存在建筑物或者构筑物时，应尽量增加二者之间的最小空间距离。

（2）增加爆破中的起爆段位能够减小爆破振动速度。本项目的起爆段位由六段增加到七段后，振动合速度至少减少13.8%。在相同段位下优化辅助眼各段的炮孔数量和装药参数能够极大降低爆破振动速度，从而达到规范和设计的振动速度控制要求。

（3）数值分析表明，基于萨道夫斯基经验公式计算的药量能得到一个初步的装药量，但是不一定能够使振动速度满足规范和设计要求，而通过数值模拟能够进一步优化装药量，使振动速度满足规范和设计要求。

参考文献：

[1]梁 瑞，包 娟，周文海，等.地铁隧道掘进爆破对既有埋地管道的动力影响[J].爆破，2021，38（1）：41-50.

[2]赵晨阳，雷明锋，施成华.大跨地铁车站爆破施工优化设计研究[J].现代隧道技术，2020，57（S1）：747-755.

[3]王海涛，金 慧，贾金青，等.地铁隧道钻爆法施工对邻近埋地管道影响的模型试验研究[J].岩石力学与工程学报，2018，37（S1）：3 332-3 339.

[4]郑爽英，杨立中.隧道爆破地震下输气管道动力响应数值试验[J].西南交通大学学报，2017，52（2）：264-271.

[5]史秀志，薛剑光，陈寿如.爆破振动特征参量的粗糙集模糊神经网络预测[J].振动与冲击，2009，28（7）：73-76，213-214.

[6]周声才，李 栋，张凤舞，等.煤层瓦斯抽采爆破卸压的钻孔布置优化分析及应用[J].岩石力学与工程学报，2013，32（4）：807-813.

[7]贾海鹏，刘殿书，方真刚，等.地铁隧道钻爆法施工中敏感区间及安全药量确定[J].北京理工大学学报，2021，41（1）：23-29.

[8]雷 振，黄永辉，陈文梦，等.爆炸冲击荷载下扩腔体积和能耗随抵抗线的变化规律研究[J].振动与冲击，2021，40（4）：66-71.

[9]杨年华.不同爆破工程的地震特点分析[J].工程爆破，2014，20（5）：1-7，17.

[10]喻 军，卢彭真，龚曉南.两种不同建筑物的振动特性分析[J].土木工程学报，2013，46（S1）：81-86.

[11]李建辉.爆破施工对邻近既有隧道的振动响应[J].建筑工程技术与设计，2021（24）：2 591-2 592.

[12]李景龙，李术才，李廷春，等.隧道下穿既有铁路爆破的稳定控制技术研究[J].岩石力学与工程学报，2007（S1）：3 596-3 600.

[13]曹淑学.隧道爆破开挖作用下洞口高边坡的动力响应[J].铁道建筑，2020，60（7）：77-80.

[14]郑明新，伍明文.爆破振动下偏压隧道洞口段边坡稳定性分析[J].铁道科学与工程学报，2019，16（8）：2 018-2 027.

[15]贾党育.隧道爆破开挖对洞口段边坡稳定性影响的数值分析[J].矿冶工程，2017，37（1）：25-28.

3441501908223