永磁电动悬浮系统三维解析建模与电磁力优化分析

巫 川 李冠醇 王 东

（海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033）

0 引言

永磁电动悬浮系统（Permanent Magnet-Electrodynamic Suspension, PM-EDS）通过永磁体与导体板相对运动在导体板内感应出涡流，与源磁场相互作用产生电磁力使永磁体悬浮于空气中，具有无摩擦、能耗低、悬浮气隙大、结构简单等优点，在磁悬浮交通、电磁发射和航天发射助推领域具有广泛的应用前景[1-2]。以美国为主的发达国家正抓紧对高速永磁电动悬浮系统关键技术进行攻关，美国通用原子能公司（GA）建造了一条基于Inductrack技术的 200m长的全尺寸试验系统，劳伦斯利弗莫尔国家实验室（LLNL）在 NASA的资助下建立了应用于航天电磁发射的悬浮系统，并取得一系列的研究成果[3]，国内的西南交通大学[2,4]、国防科技大学[3,5]、中科院电工所[6-7]等研究机构也对永磁电动悬浮技术开展了一系列研究，并建立了不同的试验平台。电磁力的准确计算是对 Halbach阵列永磁电动悬浮系统进行研究和设计的基础，结构优化是提高系统性能和减少工程化建设成本的关键，但相关的文献调研表明，在悬浮系统横向端部效应量化分析和全尺寸优化方面还需要进一步研究。

由于 Halbach永磁阵列的长和宽均有限，直线型永磁电动悬浮系统的磁场在纵向和横向都会产生畸变。这会引起在直线电机分析中广泛考虑的端部效应[8]，因此电磁场分析在系统研究设计过程中尤其重要。目前常用的电磁场分析方法为有限元法和解析法。其中，有限元法计算较为准确，尤其在一些必须考虑3-D电磁场分布的场合应用较多，但有限元法计算时间较长且对计算设备性能要求较高，不适合在系统分析设计阶段使用。针对这个问题，许多学者尝试采用解析法计算永磁电动悬浮系统的电磁场分布。目前国际上的研究者主要利用磁矢位和傅里叶空间分解法对系统的电磁场进行2-D建模分析[9-10]，但基于周期无限长的 2-D模型忽略了系统横向端部效应和纵向端部效应对电磁力的影响，这使得电磁力计算结果与实际相比有较大误差；有学者采用导体板电导率修正系数等效横向端部效应的方法求解悬浮系统所受的电磁力[11]，但修正系数只对气隙磁场的垂直分量进行了矫正，纵向分量未得到矫正，因此电磁力计算的最后结果仍存在较大误差。陈殷和 Z. B. Jonathan博士等采用二阶矢量势法对系统的三维电磁场进行建模分析[4,12-14]，但该模型基于导体板无限宽假设，导体板宽度无法得到优化。王厚生博士对有限宽导体板的三维电磁场进行了分析[6,15]，但建模过程中源磁场计算存在较大误差并且忽略了导体板横向分界面磁场透射对导体板涡流的影响。P. Subhra博士研究了横向边界面源磁场对导体板的影响[16-17]，较为准确地计算出了电磁力，但磁轮与直线形永磁阵列相比磁场分布差别较大，同时只研究了永磁体相对于导体板特定位置的电磁解析模型。目前关于系统结构参数对横向端部效应影响的研究仍存在空白，尤其是导体板宽度和永磁体宽度对系统电磁力的影响尚不明确。由于电磁力解析模型计算的限制，以往对永磁电动悬浮系统优化方面的研究多基于 2-D模型和导体板无限宽假设的3-D模型，无法对全系统尤其是导体板宽度进行优化设计[18-20]，而对于永磁电动悬浮系统，导体板铺设在轨道上，其宽度显著影响系统成本，因此明确永磁体阵列宽度和导体板宽度对系统横向端部效应的影响，将导体板宽度纳入优化过程，对系统基于工程应用背景下的轻量化和小型化研究具有重要意义。

以图1所示基于五模块Halbach阵列的永磁电动悬浮系统为研究对象，建立包含系统横向端部效应和纵向端部效应的三维电磁场解析模型，通过对比 2-D、3-D解析模型计算结果与 3-D有限元仿真结果，验证了所建三维解析模型计算结果的准确可靠性。利用三维解析模型对永磁电动悬浮系统进行参数化分析，研究结构参数对浮阻比和浮重比两个优化指标的影响。最后利用多目标粒子群优化算法（Multi-Objective Particle Swarm Optimization, MOPSO）对系统结构尺寸进行了迭代寻优，通过对比MOPSO设计解和基于参数分析的系统优化设计解，证明本文提出的优化设计方法快速可靠。

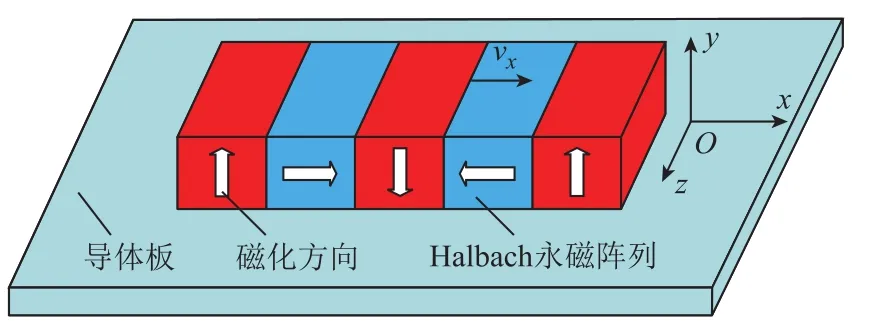
图1 永磁电动悬浮系统3-D结构示意图Fig.1 3-D structural schematic view of PM-EDS system

1 系统建模及验证

1.1 模型分析

图2为五模块Halbach阵列永磁电动悬浮系统xOy和yOz截面展开图。系统将所处的空间划分为Ⅰ～Ⅴ五个区域，各结构的尺寸参数如图2所示，其中，τ为永磁体极距，h为永磁体厚度，2w0为永磁体宽度，g为气隙，d导体板厚度，wz为导体板横向伸出宽度，l0为Halbach阵列周期延拓长度。为方便分析，对系统三维模型做如下假设[1,11,16]：①导体板在x方向无限延伸，在z方向宽度有限；②永磁体阵列位于导体板横向宽度中心，导体板厚度有限；③Halbach永磁体阵列沿x轴以速度vx运动且远小于光速，系统电磁场为似稳电磁场；④各区域的物理参数是均匀的、各向同性的。

图2 永磁电动悬浮系统xOy和yOz截面图Fig.2 The xOy and yOz section views of PM-EDS

基于Maxwell电磁场方程组和磁矢位[1-2]

经分析推导可得导体板区域的磁矢位微分方程为

式中，μ为磁导率；σ为电导率。对于非导体板域，由于电导率为0，所以其磁矢位方程为

对于导体板域，根据文献[16-17]，将导体板内的感应电流等效为源磁场分别通过边界T、B和边界e、r透射入导体板激发的感应电流的叠加结果，则导体板内磁矢位A可表示为

式中，下标 1、2表示源磁场分别通过T、B边界、e、r边界与导体板反应产生的感应场的磁矢位。

研究表明，垂直于边界面的涡流分量并不会因为源磁场的变化有明显改变[17]，且不考虑漏磁情况下垂直于源场透射边界面的涡流分量不存在[6]，因此在理想情况下解析计算可以忽略垂直于源场透射边界面的涡流分量，可以得出

1.2 边界条件

假定导体板区域和空气域的磁导率相同，在T边界面，根据安培环路定理，磁场强度的切向分量相等，即有

根据磁通连续性定理有

式中，上标r表示导体板涡流在区域Ⅱ激发的感应磁场；上标s表示永磁体激发的源磁场。B、e、r边界面的磁场衔接条件同边界面T相同。

为了实现磁矢位A各分量解耦，引入库仑规范，则有

根据文献[16]在导体板各边界面上有

其中，nⅡ为边界面的方向向量，在x方向上有

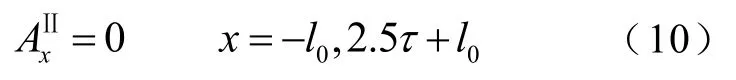
其他各区域的外层边界条件为

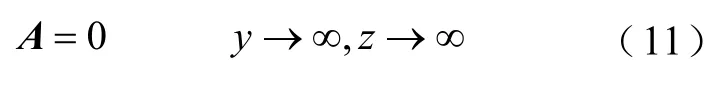
1.3 各区域磁矢位方程通解

将式（5）代入式（2），运用分离变量法[21]先求出源磁场通过上、下边界T、B与导体板反应产生的涡旋磁场磁矢位，考虑到z方向的涡流分布情况及式（9）和式（10），则区域Ⅱ中各分量的双重傅里叶级数解[16]为

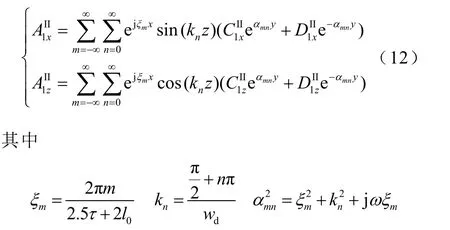
式中，2.5τ+2l0为x方向上考虑系统纵向端部效应的修正周期，认为纵向端部磁场在l0长度内衰减为0；2wd=2(w0+wz)为导体板的横向宽度。同理，区域Ⅱ中各分量的通解为

对于非导体Ⅰ区域，考虑导体板中涡流在此区域产生的磁场要与区域Ⅱ中的场一一对应[16-17]，由式（11）可解得

区域Ⅲ、Ⅳ、Ⅴ内磁矢位解的形式同区域Ⅰ类似。

1.4 源场计算

由式（6）和式（7）可以看出，在边界条件中需要源场值，采用面电流法[22]对五模块永磁体构成的 Halbach阵列的外部磁场进行建模求解，最后对源场进行双重傅里叶级数变换。分析边界条件发现，源场磁通密度的数学表达形式与磁矢位A的各分量有关。为使源场与感应场逐项关联便于求解，源场磁通密度各分量的傅里叶级数形式必须和感应场有相同本征值，因此在T边界面的源磁场经过傅里叶变换后的数学表达形式为

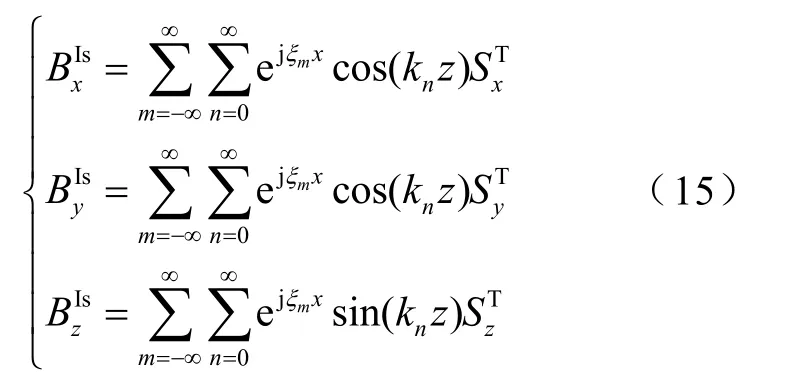
1.5 电磁力计算验证

将计算出的源场和各域磁矢位的通解代入边界条件，可求解出通解中的未知数，进而根据式（1）求出磁通密度分布，采用麦克斯韦应力张量法求解悬浮系统受到的电磁力，面T、面B受到的电磁力为F1，面e、r受到的电磁力为F2。

对于面T、B，有

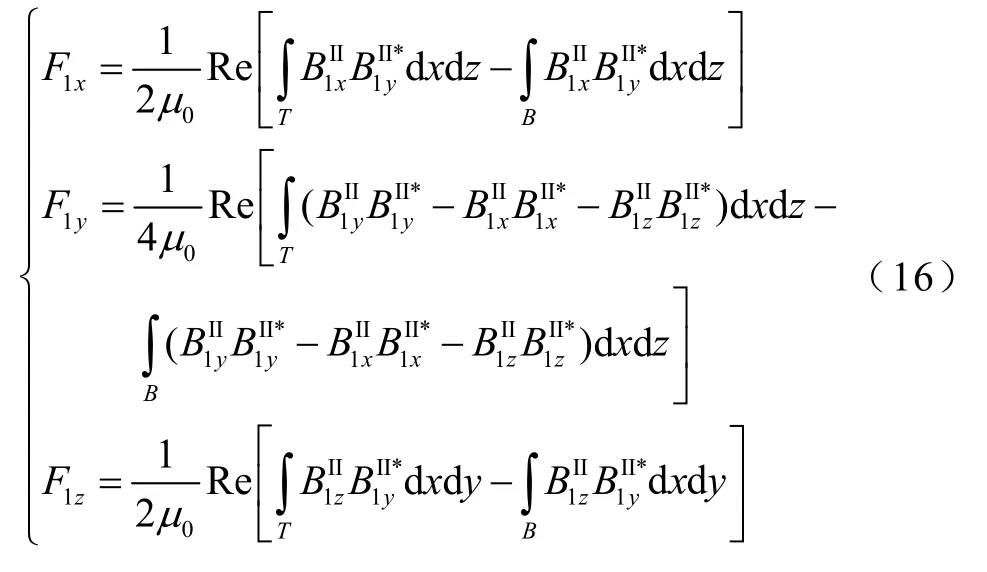
对于面e、r，有

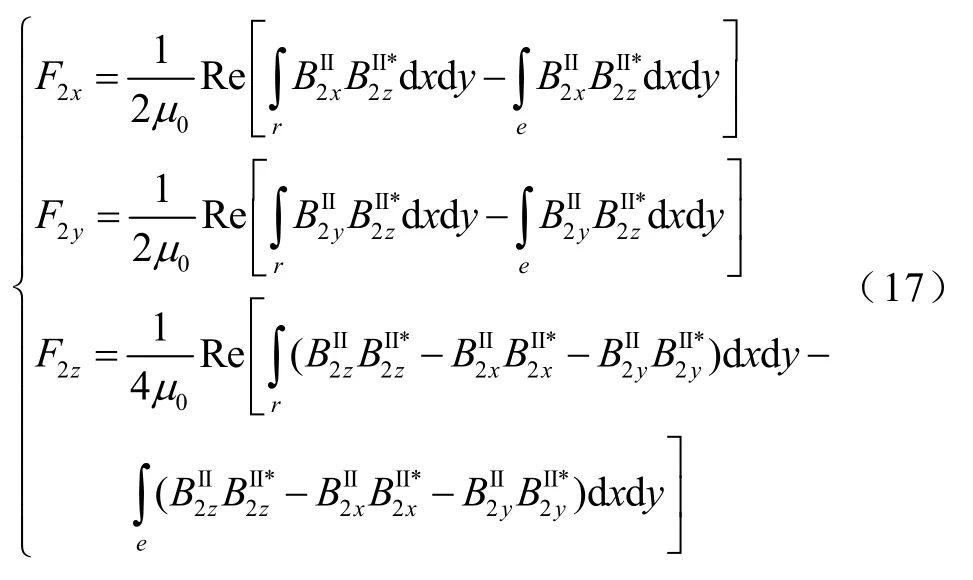
所以，导体板所受的总电磁力各方向分量为

为了验证解析模型准确性，利用Ansys Maxwell软件建立3-D有限元仿真模型，如图3所示，永磁电动悬浮系统的结构参数见表1。

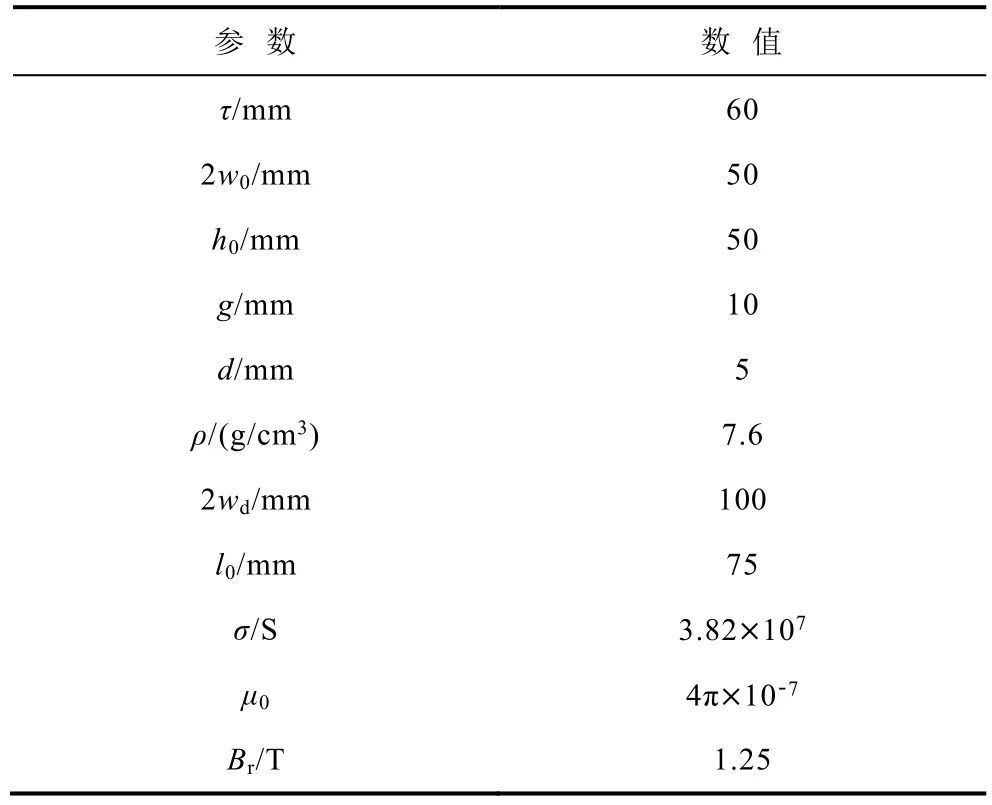
表1 永磁电动悬浮系统基本尺寸参数Tab.1 The basical parameters of PM-EDS

图3 3-D有限元模型Fig.3 3-D finite element model

图 4为二维解析模型（2D_model）[1,2,8,11,23]与本文建立的三维解析模型（3D_model）电磁力计算结果的对比，以三维有限元仿真结果（3D_FEA）作为参考标准。分析图中的计算结果可以看出，本文建立的三维解析模型相较于传统的二维解析模型能大幅度提高电磁力的计算精度，且计算结果与有限元结果基本一致，这验证了三维解析模型的计算准确性和可靠性。图5为导体板横向中心处磁感应强度沿x轴的分布情况，三维解析模型对磁场的计算结果同有限元仿真结果能较好地吻合，进一步证明了模型的准确可靠性。

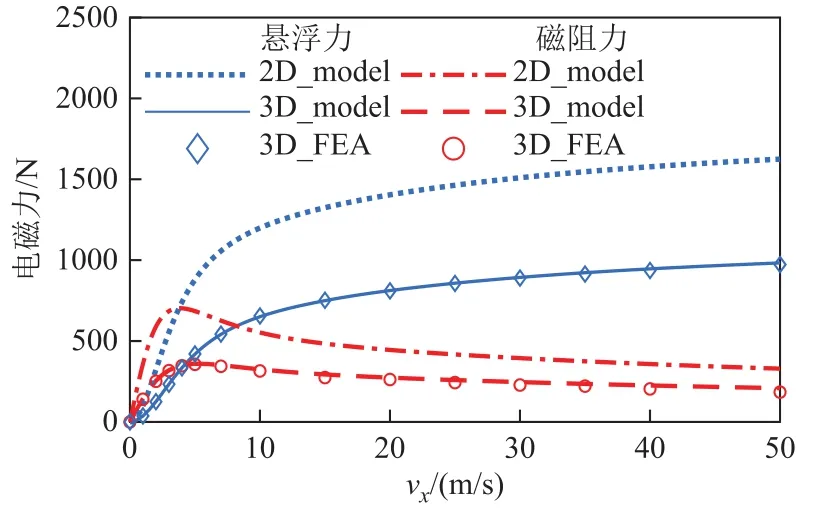
图4 不同模型电磁力计算结果对比Fig.4 The comparison of electromagnetic force calculations using different models

图6为本文建立的三维解析模型与三维有限元模型在不同导体板宽度下的电磁力计算结果。从图中可以看出，在不同导体板宽度下解析模型的电磁力计算结果与有限元仿真结果相差不大，验证了模型能够计算导体板有限宽时系统所受的电磁力，这为下一步量化分析永磁体宽度和导体板宽度对系统横向端部效应的影响奠定了基础。

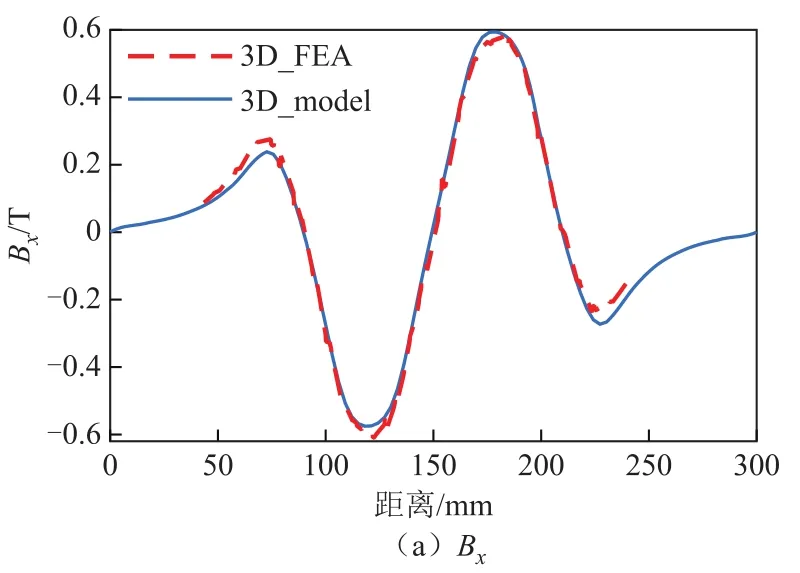
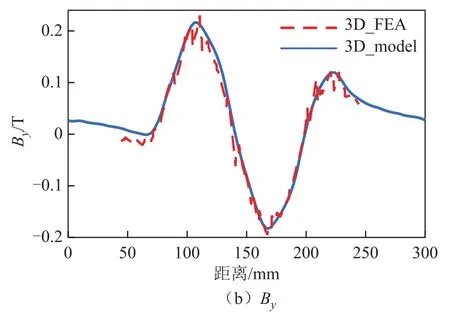
图5 磁感应强度在导体板横向中心沿x轴的分布情况Fig.5 The distribution of magnetic flux density along xaxis at center of the plate width.

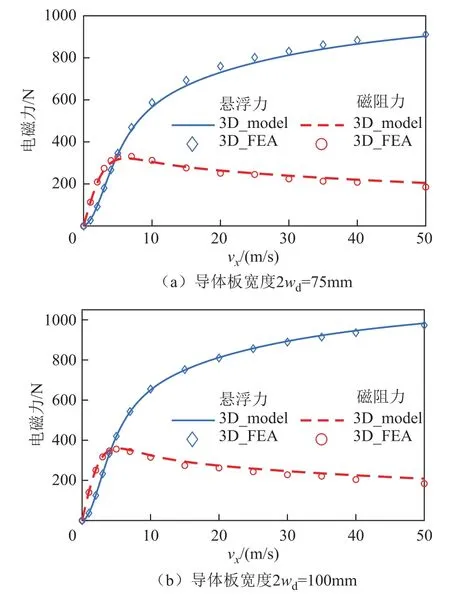
图6 不同导体板宽度下三维解析模型与有限元模型电磁力计算结果对比Fig.6 The comparison of electrimagnetic force calculations using 3D_ model and 3D_FEA in case of different conductive plate widths

2 参数分析

基于三维解析模型对系统进行参数分析，研究结构参数变化对永磁电动悬浮系统性能的影响。令永磁体阵列始终位于导体板横向宽度中心，以式（19）定义的系统浮阻比和浮重比为优化指标，改变特定参数分析优化指标受到的影响，给出最优参数取值标准。

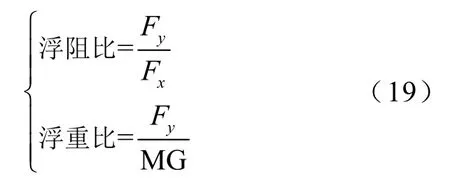
式中，Fy和Fx分别为悬浮系统所受的悬浮力和电磁阻力，已在式（18）中计算得出；MG为Halbach永磁体阵列所受的重力，可通过永磁体阵列的体积和密度直接计算。

已有的研究表明，Halbach永磁阵列单块永磁体的最优长度与气隙有关，即 Halbach的最优极距长度与气隙的选取高度有关[23]，为避免工作的重复性，本文主要研究除极距外的其他结构参数变化对系统优化指标的影响。单独研究某个参数的取值是毫无意义的，这里主要分析各参数与极距之比的最优取值标准，以保证结果的通用性。在对永磁体参数进行分析时，先将导体板宽度设定为无限宽以消除其对系统性能的影响，然后参数化分析永磁体宽度与极距之比对优化指标的影响，接着研究永磁体宽度与厚度之间是否存在耦合关系。在上述分析的基础上研究永磁体厚度与极距之比对优化指标的影响，然后分析导体板宽度与永磁体宽度之比变化对优化指标的影响，最后研究导体板厚度对优化指标的影响。最终，给出各参数的最优取值标准。

2.1 永磁体参数分析

图7和图8分别为不同极距下和不同永磁体厚度下优化指标受永磁体宽度与极距之比变化的影响。

图7表明随着永磁体宽度的增加，系统的浮重比先增大后保持不变，浮阻比基本不受影响，极距变化对最优永磁体宽度与极距之比取值无影响，2w0/τ的最优值取为2.5。通过改变永磁体厚度扫描分析永磁体宽度与厚度对系统性能的耦合影响，图8表明永磁体厚度变化对最优 2w0/τ取值基本无影响，认为永磁体宽度与厚度对系统性能的影响是彼此解耦的，因此对永磁体厚度优化的研究可采用二维解析模型以加快分析进程。

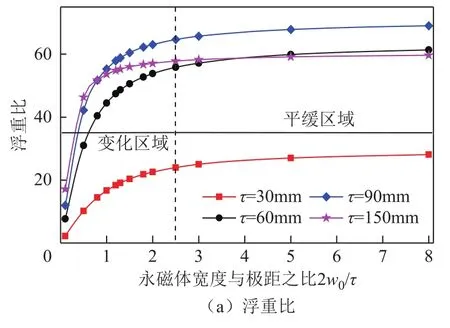
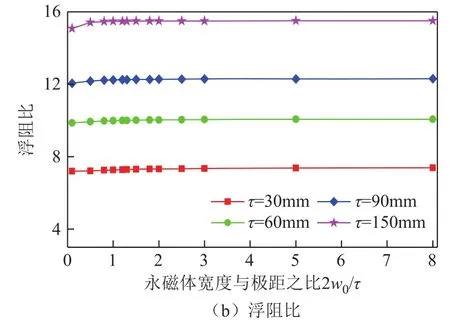
图7 不同极距下优化指标受永磁体宽度与极距之比变化的影响Fig.7 The impact of the ratio of permanent magnet width to pole pitch on optimization objectives in case of different pole pitches

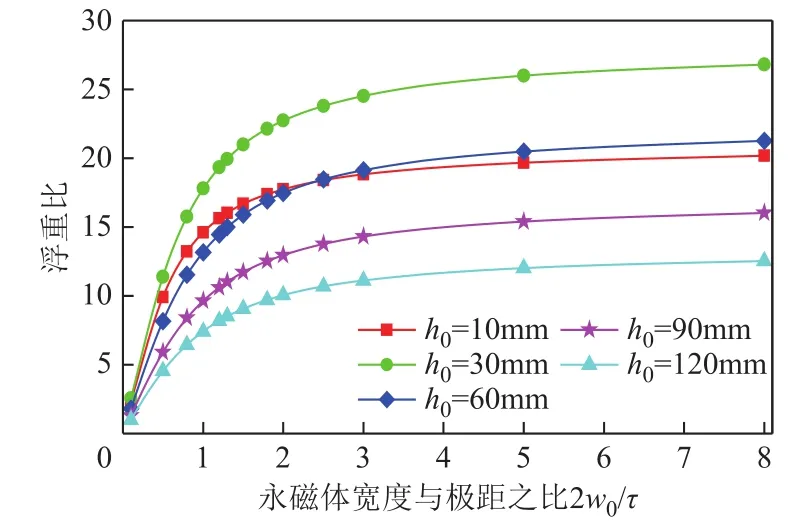
图8 不同永磁体厚度下优化指标受永磁体宽度与极距之比变化的影响Fig.8 The impact of the ratio of permanent magnet width to pole pitch on optimization objectives in case of different magnet thicknesses

不同极距下浮重比受永磁体厚度与极距之比变化的影响如图9所示。图9表明随着永磁体厚度的增加，系统的浮重比先增大后减小，永磁体厚度与极距之比（h0/τ）存在最优取值。将图中不同极距下浮重比极值和该点对应的h0/τ提取出来，绘制图10所示的最优h0/τ和极距之间的关系图，分析可以看出，随着极距的增长，h0/τ的最优取值逐渐趋近于0.4。当极距较小时，最优h0/τ较大，这是因为：在极距较小时，永磁体厚度与极距的比值要进一步增大才能使气隙磁场的纵向分量达到最大值，以获得最大浮重比。当处于浮重比极值附近时，把h0/τ的最优取值修正为0.4，画出图10中的修正线，可以看出修正值与实际值之间的浮重比最大差值不超过5%，完全可将修正值代替实际值，因此综合分析最优h0/τ取为 0.4。

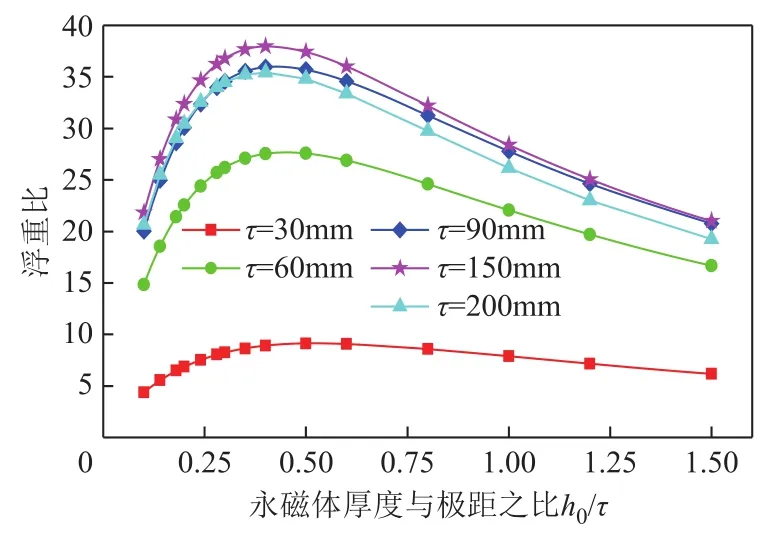
图9 不同极距下浮重比受永磁体厚度与极距之比变化的影响Fig.9 The impact of the ratio of permanent magnet thickness to pole pitch on lift to weight in case of different pole pitches

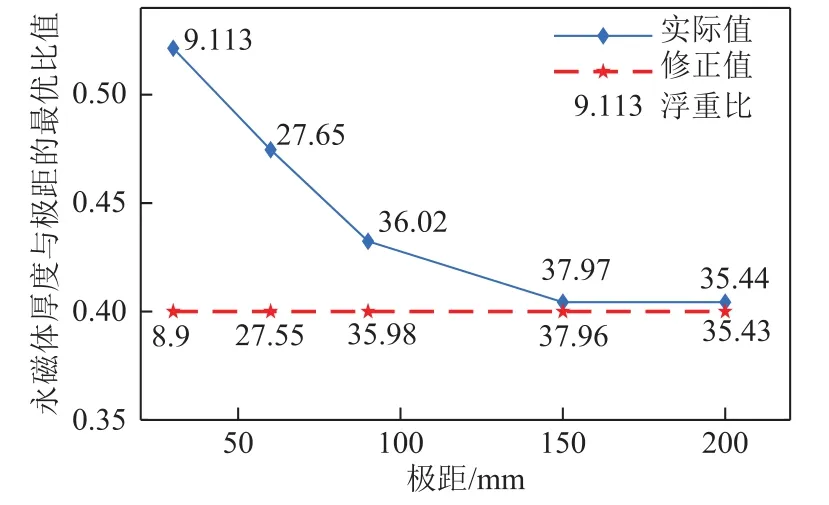
图10 极距对永磁体厚度与极距最优比值的影响Fig.10 The impact of pole pitch on the optimal ratio of permanent magnet thickness to pole pitch

2.2 导体板参数分析

永磁电动悬浮系统本质为动态感应涡流场模型，导体板的结构尺寸对涡流的分布有很大的影响，进而影响系统的电磁力。有关研究表明当磁极的横向宽度与极距之比大于一定值时，电机的端部效应可以忽略不计[8]。图11所示为不同永磁体宽度下浮重比受导体板宽度与永磁体宽度之比变化的影响。图11表明随着永磁体宽度的增加，导体板宽度对系统横向端部效应的影响逐渐变小。但考虑 2w0/τ的最优取值为2.5，在此前提下必须考虑系统的横向端部效应，分析可得最优导体板宽度与永磁体宽度之比wd/w0可取为1.5。

在涡流场分析中趋肤效应的存在会影响导体板厚度的选取，图12所示为导体板厚度对电磁阻力随速度变化的影响。图12的二维解析模型计算结果表明在低速时随着导体板厚度的增加，电磁阻力峰值会逐渐降为一个稳定值，高速时系统阻力受导体板厚度变化的影响不大，为减小推进损耗，在速度小于 50m/s的低速区间可将导体板厚度取为15mm，在中高速运动区间段可根据实际运行速度进一步减小厚度，降低建设成本。

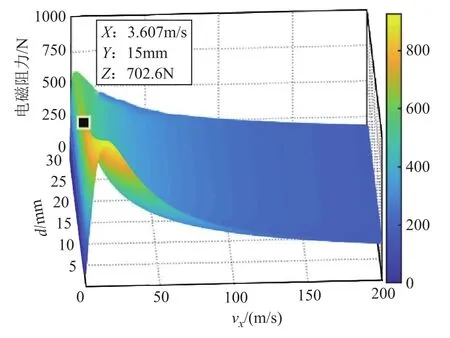
图12 导体板厚度对电磁阻力随速度变化的影响Fig.12 The impact of the conductive plate thickness on drag force changing along vx

2.3 参数分析系统优化设计法

2.1节和2.2节参数分析首次探究了导体板宽度对系统横向端部效应的影响，研究了结构参数对系统横向端部效应的影响，给出的结构参数最优取值标准可有效加快系统优化的速度，减少优化时间成本。基于参数分析系统优化设计法的永磁电动悬浮系统优化步骤总结如下：根据气隙和实际应用场景选定系统 Halbach阵列的极距，根据参数分析将永磁体的宽度取为极距的2.5倍，厚度取为极距的0.4倍。确定永磁体结构后，可将导体板宽度取为永磁体宽度的 1.5倍，对于导体板厚度，在速度小于50m/s的低速区间可将导体板的厚度取为15mm，中高速运动区间结合二维计算方法选取合适的厚度。

3 多目标优化

3.1 优化函数

利用多目标粒子群优化算法对系统的结构进行优化，优化目标为系统浮重比和浮阻比最大化，其中优化目标函数定义为

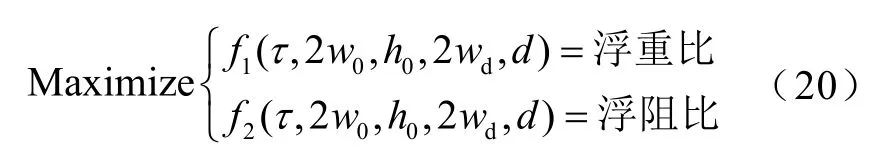
优化时，系统的运行速度vx=200m/s，g=10mm，系统结构参数组成的参数集合矢量如式（20）所示，每一个结构参数的变化范围由第 2节参数分析确定，见表2，其他参数固定不变（见表1）。

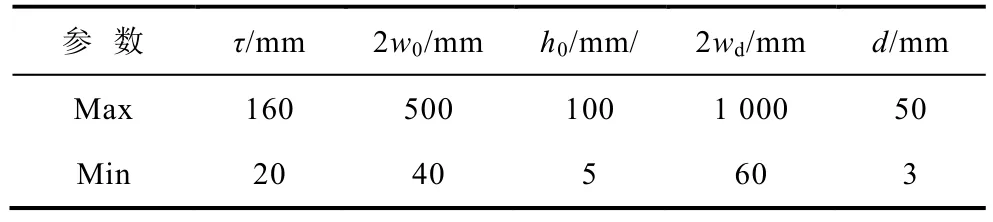
表2 优化设计参数取值范围Tab.2 The ranges of optimization design

3.2 多目标粒子群优化算法

多目标粒子群优化算法（MOPSO）目前已发展为比较成熟的优化算法之一，其算法中的粒子具备记忆功能，粒子之间可以相互交流自己存储的信息，在代表全局最优解的粒子和代表局部最优解的粒子的共同引导之下迭代寻优，最终使整个粒子群不断收敛到最优解集上。多目标粒子群优化算法的主要关系函数为[24-25]

式中，n为目前为止的迭代次数；i为种群的第i个粒子；xi为粒子的位置，即式（21）中的优化参数矢量；vi为粒子的速度，即迭代寻优时参数集合矢量的增量；Pbesti和Gbest分别为迭代过程中每个粒子的局部最优解和整个种群的全局最优解；ω为惯性权重，代表该粒子当前速度对迭代得到的该粒子的下一代位置的影响；c1为自我学习因子；c2为社会学习因子；r1和r2为0～1之间的随机数。整个种群通过迭代寻优找出合适的Pareto最优解集，画出Pareto前沿面轨迹，最后找出符合设计指标的最优解。

3.3 优化结果

将粒子的初始种群数量设置为 100，通过随机数在参数取值范围内生成100个初始化粒子，如果导体板宽度小于永磁体宽度，则将导体板宽度直接设置为永磁体宽度的 1.5倍，Pareto最优解集的大小设置为100，最大迭代次数设置为300。为了防止粒子进入局部寻优，在迭代过程中设置与迭代次数相关的突变因子，当系统生成的随机数小于突变因子时，将该粒子的本次迭代解变异为与突变因子有关的新解。

经过优化以后，Pareto前沿面轨迹如图13所示。选择其中的A、B、C三个点作为优化设计解（优化指标f1和f2），并与初始设计进行对比，其参数及性能对比见附表1中MOPSO设计解。优化点A的浮重比（55.17）和浮阻比（16.51）皆大于初始设计点（49.04, 10.04），C点的浮重比（74.12）大于A点，但浮阻比（11.14）比A点小且与初始设计点接近，B（62.25,14.47）处于整个轨迹的中点平衡处，对优化设计指标的权衡达到最佳，它及其周围的解是最佳设计目标选取区域。

图13 多目标优化Pareto前沿面Fig.13 Pareto front of the muti-objective optimization

从附表1中可以看出MOPSO优化解的导体板横向宽度较大，由优化算法寻找出来的设计解是指标最优解。此时保持A、B、C三点的极距不变，其他参数取值采用 2.3节参数分析系统优化法进行计算，得出附表1中的基于参数分析的系统优化设计解Ac、Bc、Cc，并计算出设计点的优化指标，可以看出后者的优化指标与前者基本接近，误差不超过10%，分析得到误差主要来源于参数分析系统优化法给出的结构参数计算规则，规则基础为相关指标变化的拐点值，拐点以后的增长被忽略，但优化算法计算了拐点后优化指标的增长值，同时相应的结构尺寸也大幅增大，所以最后会产生一定的误差。但从附表1的结果对比中可以看出，基于参数分析的系统优化设计解在对系统性能影响较小的情况下能大幅减小导体板的宽度，降低建设成本，且优化设计时间相比于MOPSO可以忽略不计，这验证了参数分析给出的最优参数取值标准的可靠性和实用性，减少了工程设计中的计算量，节约了设计成本，最优参数取值标准见表3。

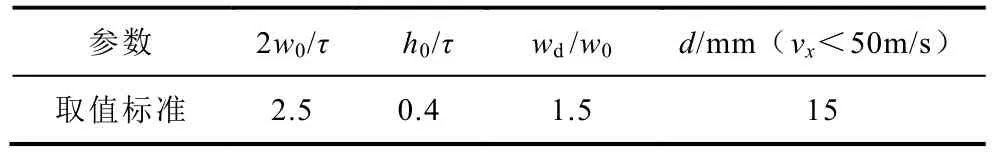
表3 最优参数取值标准Tab.3 The standard of optimization parameters calculating

4 结论

准确计算电磁力是对永磁电动悬浮系统进行深入研究和分析的基础，本文建立了直线型永磁电动悬浮系统三维电磁解析模型，考虑了系统的横向端部效应和纵向端部效应计算问题，基于构建的三维解析模型分析了结构参数对系统性能指标的影响，主要结论如下：

1）建立的三维电磁解析模型考虑了直线型永磁电动悬浮系统的横向端部效应和导体板横向边界面磁场透射对系统性能的影响，能够有效分析导体板宽度对悬浮系统性能的影响。解析模型适用于直线型永磁电动悬浮系统永磁体与导体板任意位置关系，更具通用性。与二维计算模型相比，大幅提高了电磁力计算精度，与3-D有限元仿真相比，将单个设计解的电磁力计算时间缩短为20s左右，大大节约了计算时间。

2）基于参数分析对直线型永磁电动悬浮系统的横向端部效应进行了量化研究，提出一种系统优化设计方法，得到了系统结构参数最优取值标准，见表 3。通过对比参数分析系统优化设计解和MOPSO的优化解，表明在对系统性能影响较小的情况下参数分析系统优化设计法能大幅减小导体板的宽度，降低系统建设成本，且优化设计时间相较于MOPSO计算时间可以忽略不计，减少了工程设计中的计算量，节约了设计成本。

目前作者所在的课题组正有序推进桶式旋转试验平台的建设，下一步将利用试验平台验证理论模型的准确性。

附 录

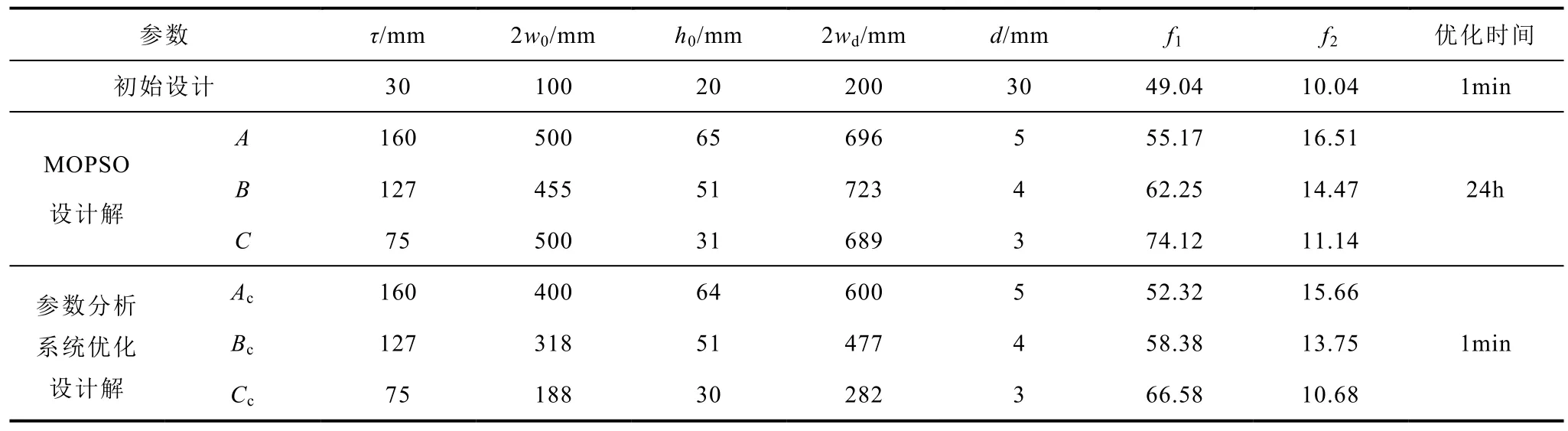
附表1 MOPSO设计解与参数分析系统优化设计解对比App.Tab.1 The comparison of design given by optimization based on parameter analysis and that given by MOPSO