直线感应电机效率优化控制技术综述

2021-03-16肖新宇董定昊唐一融

电工技术学报 2021年5期

徐伟肖新宇董定昊唐一融胡冬刘毅

（1.强电磁工程与新技术国家重点实验室（华中科技大学）武汉 430074 2. 中国中车株洲研究院有限公司株洲 412001）

0 引言

得益于无需借助机械传动结构即可实现直线运动的优势，直线感应电机在交通、工业、军事等诸多领域得到广泛应用，如城轨交通、直线伺服、电磁弹射、抽油机等[1-6]。然而受限于磁路开断、半填充槽、大气隙等因素（如图1所示），直线感应电机运行效率比传统旋转感应电机低不少，严重限制了其在大功率场合的发展应用[7-11]。同时，在许多场合（如城轨交通、传送带）下，直线感应电机长期运行于轻载状态，采用恒定励磁时其运行效率十分低下[12-13]。因此，采用合理的效率优化控制来提升直线感应电机的运行效率，意义十分重大。

基于电机参数或测量反馈等信息，效率优化控制技术通过合理调节磁链、电压、电流、转差等变量，可以实现运行效率的提升[14-15]。根据技术原理的区别，效率优化控制技术基本可分为两类：模型法和搜索法。模型法基于电机参数建立损耗模型，并求解使得损耗最小时的最优解来实现效率优化；搜索法利用迭代算法不断调整控制量（如磁链），并实时监测输入功率，直至输入功率达到最小。根据应用工况的不同，效率优化控制技术又可大致分为稳态法和暂态法两类，前者对应电机稳态运行工况，即恒定速度、恒定负载；后者则对应速度或负载变化的情况。

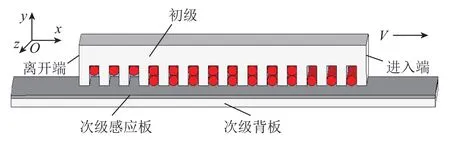
图1 直线感应电机结构示意图Fig.1 Structures of linear induction machine

受磁路开断、初次级宽度不等的影响，直线感应电机运行过程中存在横向边缘与纵向边端效应（以下简称“边端效应”），致使参数耦合严重、变化剧烈[16-18]。相比旋转感应电机，直线感应电机损耗模型更为复杂，计算求解最优控制量的难度更大。与此同时，半填充槽、大气隙的机械特征使得直线感应电机漏感比重相比旋转感应电机显著增大，因而需要特别考虑。此外，作用于初级、次级之间的法向力将影响电机视在质量，进而影响电机运行工况和控制效果[19]。总之，这些因素或导致电机损耗模型复杂度显著增大，或对搜索算法的收敛速度提出了严峻要求，进而极大地增加了直线感应电机效率优化控制技术的难度及挑战。

虽然直线感应电机和旋转感应电机的效率优化基本思路和推导过程相似，但因直线感应电机具有的大气隙、端部效应等独有的结构特点，如何准确并简炼地在数学模型和损耗模型中体现出这些特点，是直线感应电机效率优化研究过程必须关注的关键问题。

此外，在实际轨道交通中，逆变器调制频率较低，输出谐波电压成分较多，加之直线电机两端开断磁路导致的磁场畸变，从而致使电机次级磁场谐波含量较大，对电机驱动特性造成一定的负面影响。因此，在对直线感应电机进行效率优化时，如何与电机参数辨识有机结合、如何对谐波损耗进行合理分析等，也是直线感应电机效率优化亟需关注的关键问题。

本文将逐一介绍前述各类效率优化控制技术的国内外研究现状，对比旋转感应电机与直线感应电机效率优化控制技术的异同点，分析并总结迄今所存在的关键问题，同时简明扼要地讨论未来直线感应电机高效控制技术的发展方向。为便于读者理解，本文中主要参数定义见表1。

表1 本文中主要参数定义Tab.1 Definitions of main parameters in this paper

1 模型法

1.1 旋转感应电机模型法

模型法基于电机参数建立损耗模型，选取合适的控制量并求解其最优解，借助其他控制方式（如标量控制、矢量控制等）来实现效率优化控制，其基本控制框图如图2所示。可见，模型法的核心是损耗模型，其控制效果直接受损耗模型准确度影响。因而如何建立准确且实用的损耗模型，是模型法的研究关键。

图2 模型法基本控制框图Fig.2 Basic control diagram for loss model-based efficiency optimization control

针对传统旋转感应电机稳态运行工况，许多学者提出了诸多类型的损耗模型与相应的模型法效率优化控制技术，选取的优化变量包括转差、转差频率、励磁磁链和转子磁链等。文献[20]通过分析旋转感应电机单相等效电路，建立了电机铜损、铁损、气隙功率与转差s的关系，提出了相应的效率优化模型，即

式中，P1、Pc、Pg、PR分别为定子铜损、铁损、气隙功率和转子旋转损耗。实验结果显示，采用效率优化控制后，轻载时电机效率至多可提升7.46%。

文献[21]建立了包含旋转感应电机定转子铜损、铁损的损耗模型，并将其表征为关于转差频率的函数，借助牛顿-拉夫逊法求解出最优磁链后，通过矢量控制框架实现效率优化。相关电机的损耗模型为

式中，km、k1～k5为相应的系数。

文献[22]通过对稳态工况下的损耗模型线性化处理，简化了损耗模型，从而求解获得最优转差频率的一般形式，即

式中，除ωsl、ωr外，其余参数均为常系数（稳态下）。

文献[23]推导了如式（4）所示的损耗模型，并选取电压与定子角频率之比（V/ωs）作为控制量，通过遗传算法寻找最优比值。实验结果显示，相比常规控制（恒定磁链），采用效率优化控制可在0～30%负载范围内有效降低电机损耗，最高时可降低60%。

式中，Z1～Z3为相应的阻抗系数。

基于同一损耗模型，文献[24]同样选取电压与定子角频率之比作为控制量，但采用离线方法计算得到不同运行工况下的最优比值，再查表选择效率优化控制所需的最优控制参数。实验表明，在轻载时，电机效率最高可提升12%。文献[25-29]亦采用离线计算并查表选择最优控制量，但该种方法工作量大、实用性较差，现已鲜有应用。

文献[30]将杂散损耗引入损耗模型，建立了以励磁磁链为变量的旋转感应电机损耗函数，其损耗模型与最优励磁磁链分别为

式中，各系数定义详见文献[30]。该方法可直接求得最优励磁磁链的解析解，算法简单、实用性强。与传统恒压频比控制方式相比，该方法可在轻载工况下显著降低定子电压和输入功率。

文献[31-38]将转子磁链作为控制量，其中文献[31]推导并通过实验验证了电机输入功率与转子磁链之间的凸函数关系，从而证明了输入功率（或损耗）存在极小值；文献[32]借助庞特里亚金极大值原理求解获得损耗最小且时间最短的解，从而实现暂态过程的最优控制；文献[33]基于矢量控制框架，在得到包含初级、次级铜耗和铁耗的损耗模型后，基于灰狼优化算法求得最优的d轴转子磁链，从而实现最小损耗控制。文献[34]提出了式（7）所示的简化损耗模型，并借助遗传算法求解最优转子磁链。显然，由式（7）可知，该模型为关于转子磁链的凸函数。

K. Matsuse等[38]基于旋转感应电机输入、输出功率平衡，进而提出了以转子磁链为控制量且包含铁损影响的损耗模型，并推导了基于该模型的最优转子磁链解，分别如式（8）、式（9）所示。揭示了铁损对最优磁链的影响——为降低铁损，最优磁链随着转速的上升而降低。此外，文献[38]的结果表明，为实现重载下电机损耗的降低，其最优磁链要高于额定磁链。

文献[39-41]选择定子电流作为控制量，基于电机损耗模型式（10）求解获得了最优定子电流的一般形式为式（11）。

式中，Rqs为定子 q轴铁损电阻；Rq为等效 q轴电阻；Rd为等效d轴电阻，各参数具体表达式详见文献[39]。相比文献[30]中所述的方法，该方法更为简单，很容易在矢量控制框架下实现。通过实验验证，相比矢量控制，该方法可在轻载下获得 5%～50%的效率提升。同时，文献[39]还分析了效率优化控制对电机各参数的敏感性，并指出次级电阻对优化控制的效率影响最大。

虽然以上方法选取的优化变量不同，但基本只考虑了常规的铜耗和铁耗，忽略了电机漏感、饱和和逆变器等影响。实际上，电机损耗模型越准确，推导得到的最优控制量和实际最优量越接近，这样电机效率的优化及提升效果也将越好。

在式（10）模型的基础上，文献[42]进一步建立了完整包含铜损、铁损和定转子漏感影响的损耗模型。该模型认为，通过铁损支路的电流远小于励磁支路电流，因此可将铁损支路单独提取出来，从而简化等效电路与损耗计算，最终的损耗表达式为

由式（12）可见，该损耗模型相比式（10）更为全面、复杂，但两者形式一致，因此其定子电流最优解亦和式（11）具有相同的形式。此外，文献[35]还分析了在电压电流限制条件下、不同运行工况下的最优定子电流值。

实验结果显示，相比传统不考虑漏感的效率优化控制技术，文献[42]所述方法能在不同速度、转矩下进一步降低电机损耗。为简化损耗模型的推导过程，文章在损耗模型建立过程中忽略了铁损电流，从而和实际情况存在一定误差。为此，M. Uddin等[43]提出了一个较为全面、准确且简单的旋转感应电机损耗模型。推导出以转子励磁电流为参考的等效电路，并采用漏感系数将定、转子漏感等效为单一漏感，从而极大简化了转子电路部分（不含漏感），提高了损耗模型的准确度，其表达式为

式中，各等效参数定义为

为反映磁饱和对损耗的影响，进而建立更为精确的损耗模型，文献[44]将励磁电感、铁损电阻表征为关于定子磁链的非线性函数，其表达式为

式中，Lmu为未饱和时的励磁电感；β、S为正实系数；kh、ke分别为磁滞损耗与涡流损耗系数；uc为铁损电阻上的压降。文献[44]继而建立了以定子磁链sψ为变量的损耗函数为

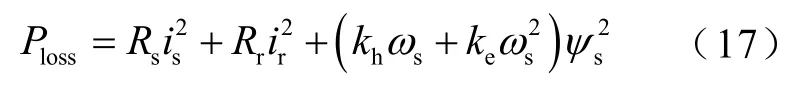
文献[44]中的仿真与实验结果显示，尽管大多数效率优化控制方法关注轻载工况下的效率提升，但效率优化控制亦可通过调节磁链使之高于额定磁链，从而提升过载时的电机效率，这与文献[38]的结论一致。

M. Piazza等[45]基于旋转感应电机动态空间矢量模型和输入输出功率平衡原理，推导了完整的感应电机损耗模型和最优磁链控制量，即

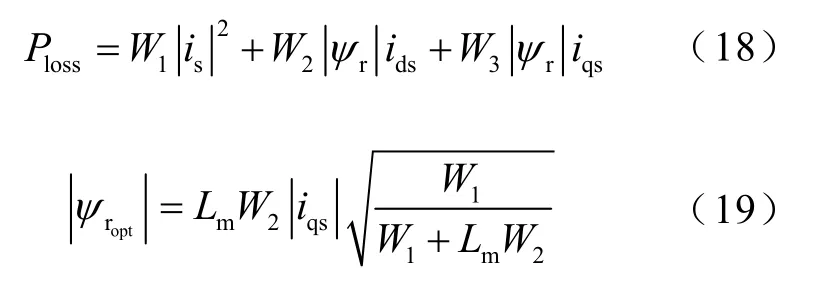
文献[46-48]同样基于输入输出功率平衡，推导并验证了任意参考坐标系下的旋转感应电机铁损模型，即

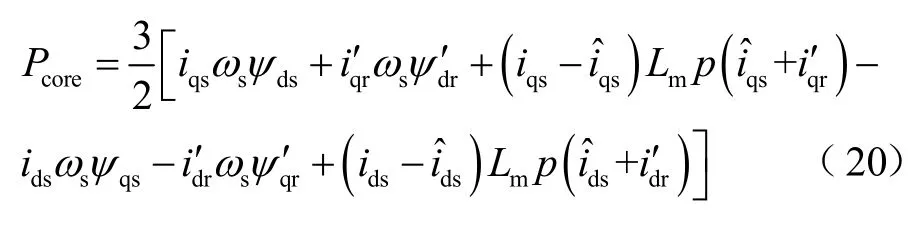
式中，相关系数的定义详见文献[45-48]。实验表明，该损耗模型在正弦供电误差小于1%，在变频供电时误差小于7%。

变频器损耗亦是旋转感应电机驱动系统损耗重要的一部分，因而降低变频器损耗将有助于提升驱动系统整体效率。文献[49]分别计算了电机铜损、铁损、杂散损耗与逆变器导通损耗、开通关断损耗，建立了相应的损耗模型，并扼要分析了温度与磁饱和对电机损耗的影响。文献[48]根据逆变器拟合特征曲线建立了逆变器损耗模型，并结合前述铁损模型建立了旋转感应电机驱动系统损耗模型。文献[50]分析了不同控制框架（矢量、直接转矩控制）下驱动系统损耗模型对不同参数的敏感性。文献[51]则分析了是否考虑逆变器损耗情况下效率优化控制的区别——只考虑电机损耗时的最优磁链比同时考虑逆变器和电机损耗时的最优磁链小，且两者的区别随着转速、开关频率的上升而增大。文献[52]分析了基于电流源逆变器的感应电机驱动系统直流母线电流与转子磁链的关系，提出了基于最优磁链控制的直流母线电流最小化方法。文献[53]则详细分析了基于电压源逆变器的旋转感应电机驱动系统各部分损耗——电机铜损、铁损、滤波电阻损耗、直流母线损耗和逆变器损耗，并通过离线方法计算获得了不同运行工况下的最优控制图。其结果表明，相比只针对电机进行效率优化控制的方法，该方法可降低7%的系统损耗。

针对传统旋转感应电机动态运行工况，亦有不少研究成果。一方面，基于动态过程损耗优化目标，文献[54-55]在假设电机转速与负载变化可知的前提下，采用离线方法计算获得了动态最优磁链，实验结果表明，相比恒定磁链控制，采用动态最优磁链控制可有效降低动态过程中的总损耗，但相应的动态过程持续时间会变长；文献[56]借助变分法求解了动态过程最优控制轨迹，但该解析解过于复杂，难以应用于实际电机控制系统；在文献[56]的基础上，文献[57-58]采用数值法获得了动态过程损耗最优的控制轨迹，并成功嵌入基于 PC处理器的控制系统中，不过该方法需多次迭代求解，计算量大，对控制系统处理器要求高，难以应用于基于DSP处理器的系统中；文献[59]推导了如式（21）所示的动态过程定子电流最优比例，并离线计算各运行工况下的近似电流比例系数，最后通过查表实现相关控制。该方法较为简单，但需要提前获取定子d、q轴电流的函数关系，并通过查表实现二者的动态分配，因而前期工作量大，通用性较差。

需要特别说明的是，由于动态过程中电机参数变化较为复杂，上述相关方法中的电机损耗模型均进行了不同程度的简化，进而降低了电机的控制难度。比如，文献[58]忽略了定转子漏感的影响，从而获得简化损耗模型为

式中，系数k1～k4具体表达式详见文献[58]。

另一方面，基于动态过程时间优化目标，文献[60-66]分别提出了不同的定子电流分配方式，其基本思路均是在限幅范围内最大程度地输出电流，以期迅速建立所需的磁场。由此可见，此时电机损耗已不再是优化目标，取而代之的是动态响应速度。此外，部分学者试图借助其他快速响应控制方法来提升效率优化控制下的电机响应速度，如无差拍控制[67-68]、滑模控制[69-70]、模型预测控制[71-72]等。整体而言，因相关方法基本上沿用前述损耗模型，故不再做赘述。

1.2 直线感应电机模型法

以上介绍的旋转感应电机效率优化控制方法，理论上可直接应用于直线感应电机。但考虑到直线感应电机磁路开断、初次级宽度不等、半填充槽、大气隙等特征，为准确地考量其损耗、更有效地提升其效率，需要针对直线感应电机所存在的特殊现象进行深入分析，推导出切合直线感应电机的损耗模型，进而提出相应的效率优化控制策略。

直线感应电机不等dq轴电路如图3所示。基于图 3，文献[73-75]建立了包含纵向边端效应影响的直线感应电机损耗模型如式（23）所示。由此可见，该损耗模型与式（10）形式一致，因而其最优初级电流求解方法同式（11）。

式中，Q为纵向边端效应因子。

图3 直线感应电机不等dq轴电路Fig.3 Unbalanced dq axis circuit of linear induction machine

基于同一不等dq轴电路，文献[76]建立了以次级磁链为变量的直线感应电机损耗模型，并获得了最优磁链解析解，即

式中，np为电机极对数；τ为极距。

更一般地，文献[77]基于直线感应电机的空间矢量等效电路，建立了以初级电流为变量，包含铜耗、铁耗及端部效应损耗的损耗模型，如式（26）所示。同样地，该损耗模型最优初级电流求解方法与式（11）相同。

式中，α和β为与电机励磁电感和次级漏感有关的变量，详细定义见文献[77]。

直线感应电机由于气隙大、励磁电感较小、初级漏感相对励磁电感的比例较大，从而对电机损耗产生一定影响。为进行定量衡量，任晋旗等[78-79]建立了如图 4所示直线感应电机 dq轴电路，其将铁损电阻置于初级漏感之前，以反映初级漏感所引起的铜损与铁损。基于该电路，文献[78-79]推导了以初级电流为控制量的直线感应电机损耗模型与相应的效率优化控制策略，具体如下。

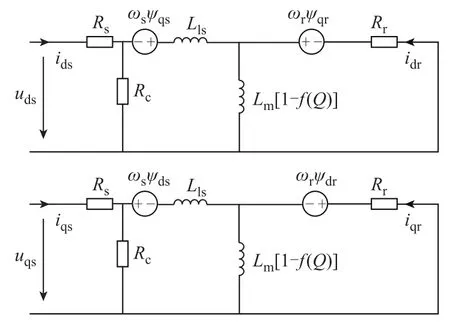
图4 含铁损的直线感应电机dq轴电路Fig.4 Linear induction machine dq axis circuit with core-loss

电机损耗模型为

最优初级电流比例为

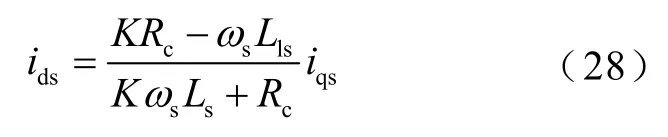
式中，系数K为

通过一台6kW弧形直线感应电机的实验得知，相比传统旋转感应电机损耗模型，新模型计算更为准确，更能客观反映直线感应电机的驱动特性。实验结果还显示，相比传统矢量控制，该效率优化控制技术可在不同速度、推力条件下有效提升电机效率，使之达到或接近额定运行效率，同时对直线感应电机动态特性没有明显的影响。

在文献[78-79]基础上，Hu Dong等[80-81]进一步提出了图5所示的直线感应电机dq轴电路：Kr、Kx为直线感应电机纵向边端效应修正系数，Cr、Cx为横向边缘效应修正系数。通过衡量直线感应电机初级、次级漏感对损耗的影响，建立了损耗模型为

式中，a1～a5为损耗系数。可见，该损耗模型同样为关于次级磁链的凸函数，即可通过求导直接获得最优次级磁链的解析解为

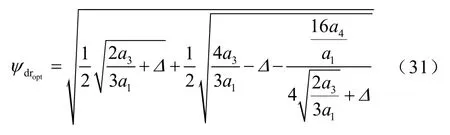
式中，Δ为与损耗系数a1～a5相关的变量，具体表达式详见文献[81]。

图5 改进的直线感应电机dq轴电路Fig.5 Improved linear induction machine dq axis circuit with core-loss

同时，文献[81]还进一步研究了考虑逆变器损耗的直线感应电机驱动系统效率优化控制技术，其逆变器损耗模型与驱动系统整体损耗模型分别为

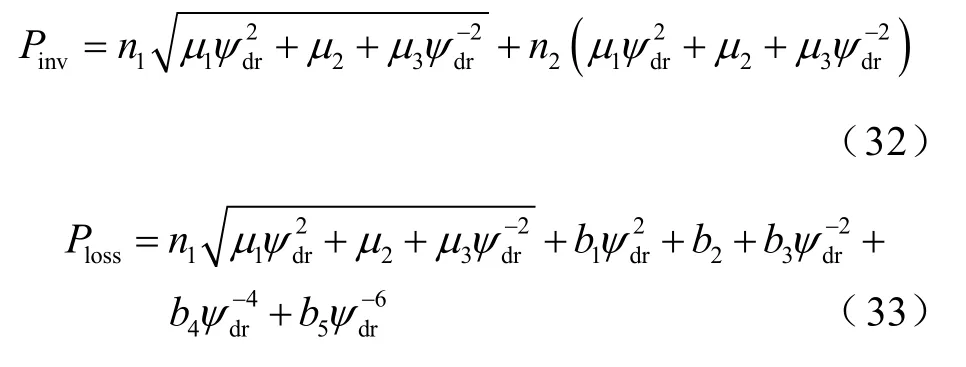
式中，系数为与电机和逆变器参数相关的变量，具体表达式详见文献[81]。由于损耗模型较复杂，文献[81]利用牛顿-拉夫逊法迭代求解直线感应电机驱动系统效率优化控制所需的最优次级磁链。通过设置式（31）所示磁链值为迭代初值，该方法仅需3、4次迭代即可获得最优磁链。其实验结果显示，相较于传统方法，该方法可降低电机损耗约3%，降低逆变器损耗约 12%，降低驱动系统总损耗约 4%。同时，其动态测试表明，该方法在多数动态工况下可满足电机的运行响应要求。

在效率优化控制中，直线感应电机法向力也是不可忽视的一部分。法向力包含斥力和吸力两部分，但多数情况下表现为吸力，且数值可达推力的5倍。法向力将显著增大电机的视在重量，进而引起损耗上升，加剧部件磨损等。文献[82]将法向力造成的摩擦力作为优化目标之一，得到优化函数为

式中，μ为摩擦系数；λ为拉格朗日因子；法向力Fn定义为

式中，ka、kr分别为法向力吸力、斥力系数。文献[82]最终得到最优磁链控制量为

文献[83-84]将转差频率作为控制量，通过离线计算获得不同速度下的最优转差频率，从而降低法向力的影响，提升磁浮列车牵引效率且对悬浮系统无明显影响。

L. Ramesh等[94]推导了直线感应电机法向力与次级磁链的关系，并提出了法向力与新型损耗优化目标函数，分别为

式中，kn为法向力系数；vr为直线感应电机线速度；fn为法向力权重系数。该目标函数右侧两项同量纲，通过调节fn即可获得不同损耗与法向力优化效果。

同时，文献[85]还分析了该模型下直线感应电机损耗、法向力对参数的敏感性。相关实验结果表明，电机损耗对参数变化鲁棒性较强，而法向力则对励磁电感、次级电阻参数依赖大。例如，当励磁电感误差为30%时，电机损耗仅上升了6%，而法向力则增大了70%。

针对动态运行工况，文献[86]提出了直线感应电机动态损耗模型为

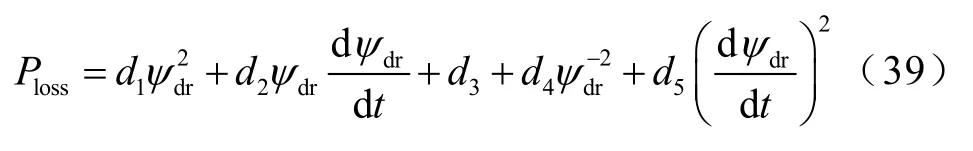
式中，各系数具体表达式详见文献[86]。

基于式（40）所示优化目标函数，文献[86]通过求解相应的欧拉-拉格朗日方程，获得了动态过程近似最优次级磁链轨迹，如式（41）所示。

式中，ψ0、ψ1分别为磁链初值与终值。相比传统方法，该方法可明显降低在线计算量。并且实验结果表明，在动态过程中，电机损耗降低 4.76%，而动态性能没受明显影响。

值得注意的是，以上介绍的多种基于损耗模型的效率优化控制方法，虽然采用搜索迭代算法来求解最优控制量，但这些方法均以损耗模型为基础，因而其本质上仍属于模型法。

2 搜索法

搜索法通过不断调节控制量（磁链、电流等）并实时监测电机输入功率，直至输入功率最小时停止。搜索法不需要电机参数，也不受电机类型限制，可选取压频比、电流和转子磁链等作为优化变量，其基本控制框图与搜索流程分别如图6和图7所示。

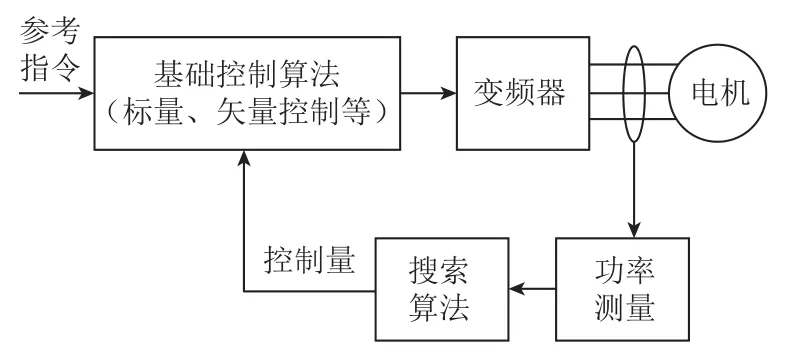
图6 搜索法基本控制框图Fig.6 Basic control diagram for search controller-based efficiency optimization control

文献[87]选择压频比作为控制量，从额定电压和额定频率开始搜索，逐渐降低电压、增大频率，从而降低磁链，直至获得最小损耗。其结果显示，轻载时电机效率可提升12%，但搜索迭代过程长达数分钟。文献[88]同样选择压频比作为控制量，不同之处在于其先调整频率使速度达到参考值后，再降低电压，从而实现输入功率降低。

图7 搜索流程Fig.7 Flow chart of search controller

文献[89]则选择转子磁链作为控制量，按0.04(pu)的幅度递减搜索最优磁链，并基于矢量控制框架实现电机效率优化。其搜索时间约7s，可降低输入功率约3.6%。文献[90-93]分别采用斐波那契算法、黄金分割法和梯度法来加快搜索收敛速度，其收敛时间最快可缩短至1s以内。

除了常规的迭代搜索方法，搜索法也可与现代优化方法相结合。文献[94-98]借助模糊逻辑控制器来搜索最优控制量。其中，文献[94]将定子 d轴电流作为搜索对象，建立了输入功率变化与定子d轴电流变化之间的隶属函数，并用其来确定定子d轴电流的调整方向（增大或减小），其搜索时间约为7s。文献[95]则采用动态更新的隶属函数，借助神经模糊逻辑控制器搜索定子电压最优值。结果显示，低速时该方法可提升电机效率约 27%。文献[96]采用罗森布鲁克法迭代搜索定子d轴电流，并通过监测直流母线功率来确定最优电流，从而实现驱动系统效率最优。该方法的迭代原理为

式中，ΔP(n)为第n次测量功率与前一测量值的比较。实验结果表明，该方法的搜索时间约为15s。

文献[99]将黄金分割法应用于直线感应电机，搜索确定初级d轴电流与初级q轴电流之间的最优比例，并基于矢量控制框架实现直线感应电机效率优化。该方法搜索时间约2s，且电机负载变化时无需重新启动搜索，在一定程度上降低了电流的波动。文献[100]同样将初级电流作为搜索优化对象，但采用直接推力控制框架，以期在实现直线感应电机效率提升的同时获得较好的推力响应，其搜索收敛时间约为2s。

3 讨论

3.1 两类方法对比

鉴于上述介绍，可对模型法、搜索法这两类方法进行简要总结，具体如下。

（1）搜索法不受电机种类与参数影响，但有迭代收敛要求，且收敛时间一般较长（数秒以上），在线计算量大，对硬件要求高。

（2）由于电机损耗曲线在最小值附近较为平坦，因而搜索法在最优值附近易出现反复寻优，从而引发电流、转矩波动。

（3）搜索法受电机功率等级影响较为明显。这是由于大功率电机通常惯性大，每一次迭代调整控制量后恢复至稳态的时间更长，从而致使整个搜索过程时间变长。

（4）模型法无收敛要求，计算快（数毫秒至数十毫秒），对硬件要求低，但受电机类型和参数影响较明显，从而影响优化效果。

（5）得益于计算快的优势，动态工况下更适合采用模型法。同时需要指出的是，多数动态工况下，优先关注的是响应速度而非损耗。

两类方法的具体对比结果见表2。

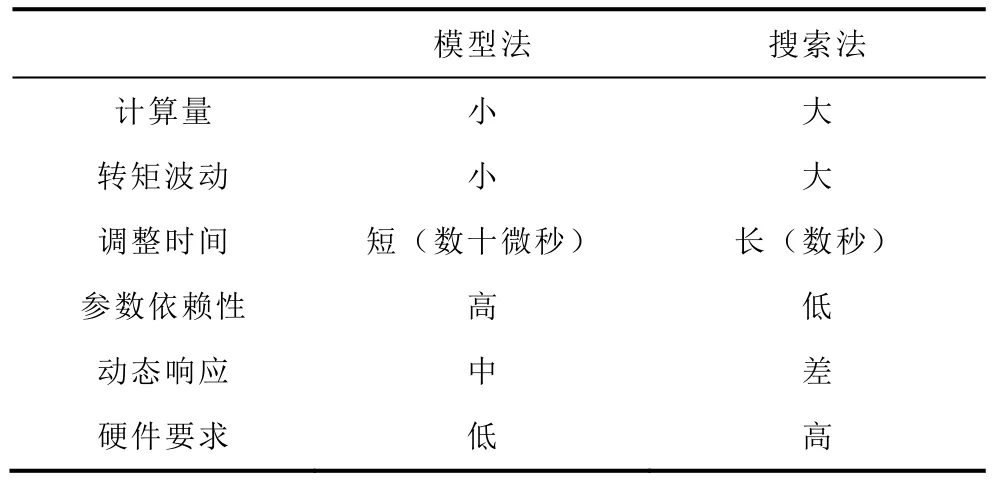
表2 模型法与搜索法对比Tab. 2 Comparison between model and search methods

3.2 直线感应电机效率优化控制关键问题

（1）直线感应电机受边端效应影响，励磁电感、次级电阻参数变化剧烈且复杂。因此，对于直线感应电机模型法效率优化控制技术而言，准确描述参数变化是提升优化效果的关键点。一方面，参数变化导致计算最优控制量偏离实际最优量；另一方面，为准确反映参数的变化，损耗模型复杂度将增加，致使求解困难。因此，如何在不影响效率优化效果的前提下，对电机数学模型和损耗模型做出适当简化，是未来发展的一个重要方向。

（2）直线感应电机模型法效率优化控制技术面临通用性问题。不同电机制造材料、工艺存在差异，运行工况千差万别，致使电机损耗模型不尽相同。例如，城轨交通直线感应电机的气隙磁通密度通常较低、运行速度也较低（通常不高于 80km/h），因而铁损占比较小；但由于其气隙特别大（通常不低于10mm），导致初级漏感占比大，从而对损耗模型产生影响。而对结合变频器损耗的直线感应电机驱动系统模型法效率优化控制技术而言，这一问题尤为严重——变频器拓扑与调制方式都将直接影响损耗模型的精度。如何提升模型法的通用性问题，如何与参数辨识方法有机结合，也是未来发展的重要方向。

（3）谐波同样影响模型法效率优化控制效果。前述损耗模型都基于基波模型而建立，而在谐波影响下，所得到的计算最优控制量并非实际最优量。由于磁路开断、初级半填充槽、边端效应等特征，直线感应电机在实际运行中面临三相不平衡等问题，其谐波对驱动性能的影响相对旋转感应电机更为突出。因此，合理考虑谐波影响的效率优化方法也亟需进行研究。

（4）受制于收敛速度，搜索法应用较少。提升搜索算法收敛速度，并降低搜索过程中电流、转矩（推力）波动，是搜索法一直面临的难题。值得庆幸的是，近年来微处理器的快速发展，将不断提高效率优化控制技术的实用性，并进一步拓展其应用范围。因此，搜索法有望在未来得到一定的应用。