深度学习模型融合正则化方法在高维数据特征筛选中的应用研究*

王 萌 王 策 栗思思 卢宇红 宋佳丽 李 康 侯 艳△

【提 要】 目的 探索基于深度学习模型联合正则化方法在小样本高维数据特征筛选中的优势。方法 通过模拟实验和实际数据分析比较深度学习模型单独及联合正则化方法在小样本高维特征筛选准确性方面的差异；采用测试集中C指数作为两种模型泛化能力评价指标。结果 在小样本研究中单纯的深度学习模型在变量之间存在复杂相关性时会表现过拟合，而深度学习模型联合正则化的方法比单独的深度学习模型在测试集中体现出防止过拟合的作用，具有更好的泛化能力。通过比较不同正则化的方法，发现深度学习联合组 lasso相比于lasso在测试集中表现出更好的泛化能力。结论 深度学习模型联合正则化的方法在小样本高维数据特征筛选中可以防止过拟合，保证外部测试具有较好的预测效果。

模型介绍

深度学习模型融合正则化方法是指在常规深度学习的输入层与第一隐藏层之间加入正则化方法，剔除对结局变量作用较小的特征组，从而进行特征筛选，以保证使用较少且重要的特征来训练深度学习模型，避免出现过拟合现象[4]。深度学习与正则化融合方法的示意图如图1所示。由于高维组学数据具有特征个数较多、样本量少、数据结构较为复杂等特点，传统的深度学习模型学习数据的特征时常常尝试兼顾所有的数据点，很容易出现过拟合现象。考虑在深度学习模型学习特征的信息前首先利用正则化方法对高维组学数据筛选出对结局变量影响较大的特征，再作为输入变量放入深度学习结构中，可能会具有更为有效的防止过拟合，同时提高模型学习效率等优点。

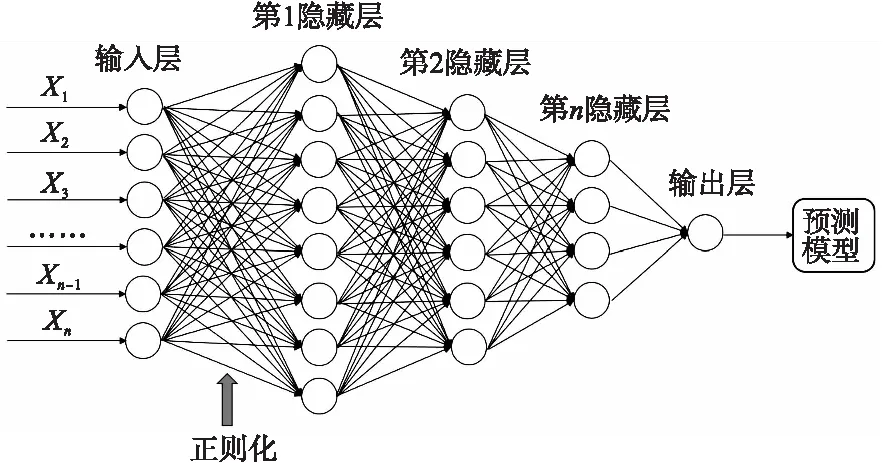
图1 深度学习与正则化融合方法的示意图

1963年Tikhonov提出正则化不但具有降维的作用[5]，同时可以有效防止模型过拟合[6]。正则化主要思想是在估计参数时，引导损失函数的最小值朝着约束方向迭代。正则化的方法有很多，例如lasso、自适应lasso、弹性网等，近年来由于组lasso(group lasso)能够实现生物学有对结局指标类别的筛选，即筛选出对结局变量影响较大的特征组，进而在此类特征组中进一步筛选特征，此种思想在实际应用中较为常用[7]。以下为组lasso的参数估计表达式：

(1)

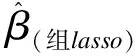
深度学习模型输出层的特征是综合全部特征变量的信息筛选得到的一个或多个特征，将其与各类模型相结合进行有效地预测，便于评估筛选变量结果准确性的指标。本文通过模拟实验和实例数据来评价深度学习联合正则化是否可以筛选出有效特征，提高模型的泛化能力。

模拟实验

1.模拟数据的产生

(1)特征数与样本含量的设定

在实际的组学数据中常常具有成千上万个基因，增加了数据处理与分析的困难性，为了使模拟数据与TCGA中真实的数据结构相似且便于计算，我们在模拟实验中设置特征的个数p=800，样本量n=500，此时符合实际组学数据中基因的数量远远多于患者数量的特点。

梅黎明指出，“乡村振兴战略的内涵十分丰富，将‘四化’同步发展提升为‘农业农村优先发展’，将‘社会主义新农村建设’提升为‘乡村振兴战略’，将‘农业现代化’提升为‘农业农村现代化’，将‘统筹城乡’提升为‘城乡融合’。”

(2)特征组的设定

考虑到组学数据中特征间具有相关性，在分析数据时应将具有相关性的特征分为一组，在模拟实验中设每个组内有4个特征，即将8000个特征平均分为2000个组，同时假定5个组即20个特征对生存有影响。

(3)生存时间及生存结局的设定

本文以Cox比例风险模型作为深度学习模型的预测模型探索方法的有效性，这里模拟500名患者的生存时间和生存结局。每个患者潜在生存时间可表示为：

(2)

βX={β1X1，β2X2，…，βg-1Xg-1，βgXg}

共有g个组，在第j个特征组中：

βjxj={βj1xj1，βj2xj2，βj3xj3，βj4xj4}

1≤j≤g，βj1xj1，βj2xj2，βj3xj3，βj4xj4为第j组内4个特征及其系数。设T1为服从参数为λ指数分布的删失时间，若T1≥T，则生存结局为死亡；若T1

2.评价方法及指标

随机抽取数据集的60%、20%和20%分别作为训练集、测试集和验证集，训练次数为5000次。首先在训练集中训练深度学习模型，然后在验证集中采用梯度下降法不断对模型的超参数进行调整，寻求最佳模型，最后在测试集中评估其泛化能力。选择测试集中C指数客观地评估深度学习模型单独及联合正则化方法后的泛化能力。

3.模拟实验的结果

使用模拟数据集分别训练联合组lasso和lasso的深度学习模型与单纯的深度学习模型，每经过一次训练后记录训练集、验证集和测试集中的C指数，随着训练次数的增加，相应的C指数发生改变如图2所示。

图2反应了不同模型的训练过程中，训练集、验证集和测试集中C指数的变化情况。训练未加入正则化的深度学习模型时(图A所示)，验证集和测试集C指数无明显波动，由表1可知当不同数据集的C指数保持不变时，训练集的C指数较验证集和测试集中C指数0.62高的多，由此可见，未加入正则化深度学习的模型存在过拟合的风险，可能不具有较好的泛化能力。加入lasso(图B所示)和组lasso(图C所示)的深度学习模型在训练过程中验证集和测试集的C指数均有显著增大的趋势，且训练分别至约为2000次和3000次，验证集和测试集的C指数趋向稳定。图B和图C中测试集C指数达到稳定时分别为0.80和0.88。深度学习模型中加入正则化，通过在训练集中不断训练以及在验证集中对模型超参数的不断调整获得的深度学习模型具有很好的泛化能力，在一定程度上可以有效防止训练深度学习模型时出现过拟合，且组lasso防止模型过拟合的效果优于lasso。

图2 不同模型训练集、验证集和测试集中C指数随训练次数增加的变化情况

表1 相同模型不同情况下三个数据集中稳定的C指数

实例分析

1.数据的来源及整理

从TCGA癌症基因库中下载共计630名卵巢癌患者的mRNA、蛋白质组学以及临床信息，将模拟实验中所阐述的方法及评价指标应用于上述实例数据。在上述数据中选择原发卵巢癌患者同时剔除缺失生存结局、生存时间的患者，最终保留196名包含有组学数据和临床信息的原发卵巢癌患者；剔除大于等于70%患者中缺失的特征，若小于70%的患者缺失某个特征值，对其缺失值采取中位数填补[9]。对填补缺失值后的组学数据进行Z标准化。在实例数据中，共有18717个特征，mRNA和蛋白组学中受同一基因调控的特征分为一个特征组。

2.实例分析结果

如图3所示，随着训练次数不断增加，同时模型在不断的优化，此时融入组lasso模型测试集的C指数明显增加，最高可达到0.67，且明显高于常规深度学习模型测试集的C指数。对两种模型测试集C指数的中位数进行Wilcoxon秩和检验，检验得到的P值小于0.0001，二者中位数的差值具有统计学意义，即融入组 lasso模型的测试集C指数中位数高于常规深度学习模型的测试集C指数的中位数。由此可见在模型中加入组lasso可以提高模型的C指数，且融入组lasso模型相比于常规深度学习模型具有更好的泛化能力，过拟合风险相对更低。

图3 未加入正则化与融入组 lasso两种模型测试集C指数随训练次数的变化

讨 论

实验结果显示，使用常规深度学习模型进行预测时模型的C指数中位数仅为0.57，且模型验证集的损失函数并没有减小，此时模型存在过拟合。实际中癌症高维组学数据的样本量较少且与结局变量无关的特征较多是导致深度模型出现过拟合的主要原因。在训练常规的深度学习模型时需要大量的样本，但是在实际癌症组学数据的研究中，样本量较少限制了模型的学习能力，与此同时数据中又存在大量与结局变量无关的特征，因此模型不能充分且有效地学习从而导致模型的预测性能降低。此时我们需要正则化方法对癌症高维组学数据进行降维，为训练模型选择与结局变量高度相关的特征或者特征组(癌症高维组学数据中具有分组信息)，在样本量较少的情况下提高模型的学习效率和预测的准确性，降低模型过拟合的风险。

实际癌症高维组学数据中，大部分特征都不是相互独立的，常规的深度学习模型并不能对彼此之间具有相关性的输入特征进行分组，所以加入组lasso的深度学习模型更适合处理实际的癌症高维组学数据。众所周知，实际癌症组学数据中特征个数以及它们之间的相关性使数据结构较为复杂，在模拟实验中是将所有特征均匀分组，即每特征组中特征个数相等，而在卵巢癌患者的组学数据中某些基因可能同时调控多个组学的不同特征，亦可能仅调控一个组学特征，因此并不能保证每个特征分组内的特征个数相等，在一定程度上也增加了数据结构的复杂性。但模型中融入正则化方法可以使模型在小样本的数据中具有较强的学习能力，防止模型过拟合，减少无用功，节约运算时间。

虽然本研究通过在深度学习模型中加入正则化方法使得在实际组学数据中训练模型较少的出现过拟合，但是如果将同一通路中组学特征分为一组，需要考虑同一组学特征出现在不同的通路中，换言之，同一特征同时出现在不同的特征组中时，本文所述的lasso、组lasso不再适用，它们能够改善过拟合的问题，但不能彻底解决，在未来的研究中我们尝试将重叠lasso应用于深度学习模型中，改善用组间具有重叠特征的组学数据训练深度学习模型时出现的过拟合问题。随着高维组学数据研究不断发展，正则化方法在进行高维特征筛选方面具有较好的应用前景。