小型甘蔗收获机振动特性的研究与分析

2021-03-16何桂庆莫瀚宁曹铂潇

装备制造技术 2021年11期

何桂庆，赖晓，莫瀚宁，2＊，曾邦，曹铂潇，滕筱

（1.广西大学，机械工程学院，广西南宁 530004 2.梧州学院，机械与资源工程学院，广西梧州 543000）

0 引言

甘蔗是我国重要的经济作物，而甘蔗产量直接影响着蔗农的收入，由于人工收获的成本居高不下，甘蔗收获机的研发与推广就越来越受到人们的重视。但机械化收获时，甘蔗的宿根破头率高是严重影响甘蔗收获机研制和推广的瓶颈问题之一。现有甘蔗收获机切割甘蔗时的宿根破头率高达20%[1]。很多国内外学者对甘蔗收获机切割系统的动态特性、甘蔗蔸破头原理进行了研究。美国Valco TD 等[2]进行了高压水切割甘蔗试验，结果发现，高压水切割甘蔗仅限于在室内可行而田间作业时并非理想的切割方式；Mello 等[3]通过高速摄像对比分析了弯角形刀片和光刃刀片的切割效果，结果发现，弯角形刀片比光刃刀片更有利于减少切割损失，提高切割质量；蒙必胜[4]对甘蔗收割机部分结构参数与工作参数影响宿根破头率破的机理进行了研究，同时提出参数计算公式及优化措施。杨家军等[5]通过混合模态综合法建立了小型甘蔗收割机的整体动力学模型，并在该模型的基础上对其切割器进行动态结构设计。上述研究仅对刀盘和刀片的结构参数、工作参数进行优化，而在动载荷冲击的情况下甘蔗破损率过高的原理还未从得知，也未曾从动态响应的角度考虑各种激励载荷的影响规律，其中切割系统与车架连接方式、液压缸的结构参数的变化等均会影响动态特性和刀盘振幅。

本研究以多体动力学为理论基础建立整机的动力学模型和虚拟样机模型，多工况下求解切割器的动态响应，以此分析各激振源对振动的影响规律。

1 建立力学模型

甘蔗收获机切割系统主要受到路面不平度激振、发动机周期激振和砍蔗力激振等激励源的影响，但是激振源安装位置，整机刚度和质量分布对整机动态特性的影响也相当显著。因此，为了探究激振源安装位置，整机刚度和质量分布对甘蔗收获机切割系统振动的影响，将甘蔗收获机整机简化为质量—弹簧—阻尼系统[6]，四个车轮简化为弹簧阻尼，如图1 所示。基于对甘蔗切割质量的敏感性，该动力学模型只考虑垂向振动（沿Z向移动）、横向扭振（绕Y轴转动）和纵向扭振（绕X轴转动）三个方向的自由度，则动力学模型存在车架质心垂向位移X1、绕X轴质心转角θ1、绕Y轴质心转角θ2，以及发动机质心垂向位移X2和切割系统垂向位移X3共5 个自由度。

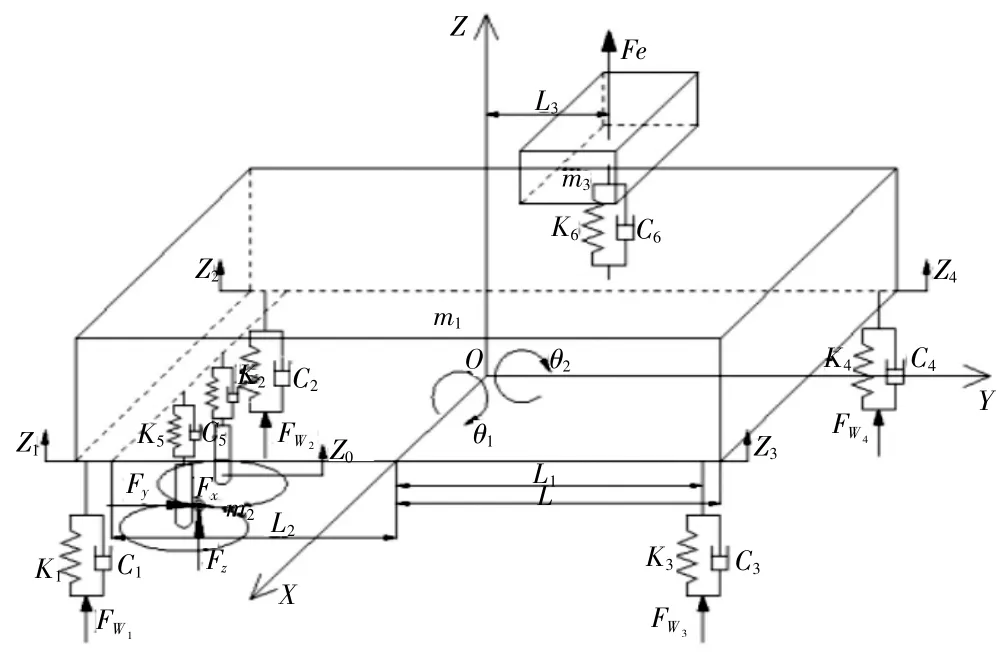
图1 甘蔗收获机5 自由度动力学模型

各符号含义，m1、m2、m3分别为：车架质量、切割系统质量、发动机质量；K1、K2、C1、C2分别为：前导向轮的刚度、阻尼；K3、K4、C3、C4分别为：后驱动轮的刚度、阻尼；K5、C5分别为：切割系统和车架之间提升液压缸的刚度、阻尼；K6、C6分别为：发动机悬置的刚度、阻尼；Fwi为各车轮受到的路面不平度激励载荷；Fe为发动机垂向激振力；Fx为径向切割力；Fy为切向切割力；Fz为轴向切割力；L为车架长度距离的一半；L1为前轮或后轮到车架质心的距离；L2为切割系统到车架质心的距离；L3为发动机质心到车架质心的距离；zi为各车轮的垂直向位移；zq为切割系统的垂向位移；θ1为车架绕质心的纵向转角；θ2为车架绕质心的横向转角；垂直向上为正方向，ζ为路面不平度拟合函数，此为简支梁形式的力学模型，建立以下方程。

Z5为提升液压缸和车架连接点的铅锤位移（向上），Z6为发动机的位移（铅锤向上），Z7为车架位移（铅锤向上）可得

式中a为1/2 前后轮距，ye为发动机对车架的激振力到车架质心的距离，可得：

将（11）、（12）、（13）、（14）、（15）式矩阵化为MZ¨+CZ˙+KZ=F得整机的数学模型：

式中，M、C、K分别为质量矩阵、阻尼矩阵、刚度矩阵；Z、Z˙、Z¨分别为广义坐标位移矩阵、广义速度矩阵、广义加速度矩阵；F为广义力矩阵。

通过分析甘蔗收获机5 自由度动力学简化模型，发现甘蔗收获机各部件的质量、安装位置变化都会对矩阵产生影响，从而影响砍蔗系统的动态响应。由于直接求解砍蔗系统的动力学微分方程组比较困难，而且对于多种激励作用下砍蔗系统动态响应求解更加困难，因此考虑使用多体动力学软件进行求解。

2 复杂激励分析

复杂激振工况下激振源主要包括路面不平度激励、发动机激振力和砍蔗切削力。课题组前期已经使用五轮仪法采集

广西丘陵地区甘蔗产地的路谱信号，再通过去均值滤波、积分得到路谱激励的位移信号，如2 图所示[9]，利用Matlab 工具箱的功能组件cftool 对课题组前期试验测量的路面不平度时域信号进行最高阶为8 阶的函数拟合，拟合的结果如图2 曲线X（t）所示，该拟合函数是由八个正弦函数叠加而成的，其表达式见式（16）。由位移函数可进一步推导出甘蔗收获机受到路面不平度的激振力，如式（17）所示。甘蔗收获机样机的发动机采用四缸直列柴油发动机YCD4J22T-95[10]，其往复激振力可由式（18）计算。由前期大量试验研究结果发现，砍蔗力可由经验公式（19）计算。

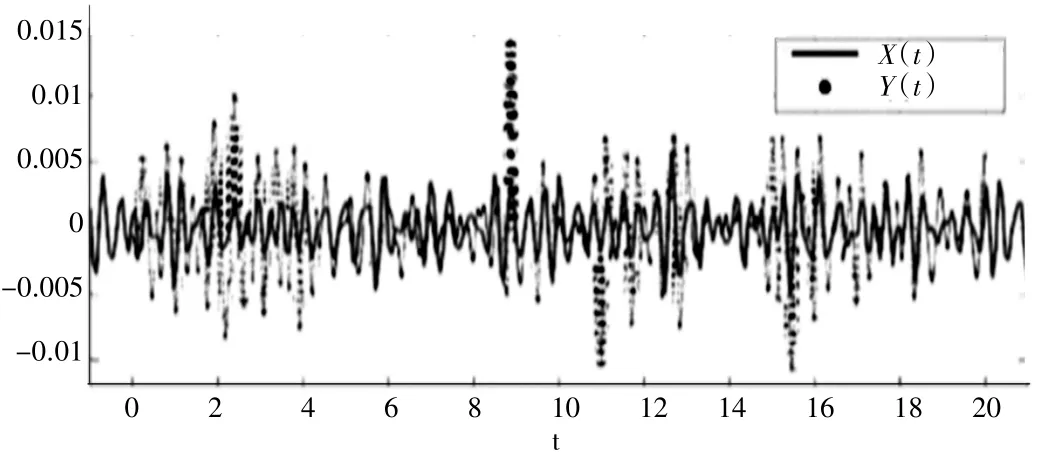
图2 路面激励拟合函数曲线

其中ai，bi和ci为拟合常数。

式中，v为刀盘转速，r为刀盘半径，θ为刀盘倾角。

3 虚拟样机仿真

3.1 建立仿真模型

由于刀架垂直方向上的振动对切割质量的影响最为重要，因此仿真试验只研究路面激励、发动机激励和砍蔗激励共同作用下刀架在竖直方向上的振动特性，并忽略水平方向的振动位移。通过使用Solidworks 三维绘图软件设计甘蔗收获机的模型（图3）后，保存为Parasolid（*.x_t）格式文件后导入ADAMS 虚拟样机仿真软件，如图3 所示。模型车架部分的质量设置为m1，物流架部分设置为m2，切割系统质量设置为m3，发动机质量为m4。前导向轮和后驱动轮的刚度和阻尼系数采用课题组前期研究的参数，液压提升油缸和发动机悬置可视为弹簧阻尼连接[9-11]，各弹性连接的刚度和阻尼系数（表1）。发动机频率为50 Hz，且动态幅值±0.1 mm 时，其动刚度系数为1 980 N/mm，粘性阻尼系数为0.15 N/（mm/s）。

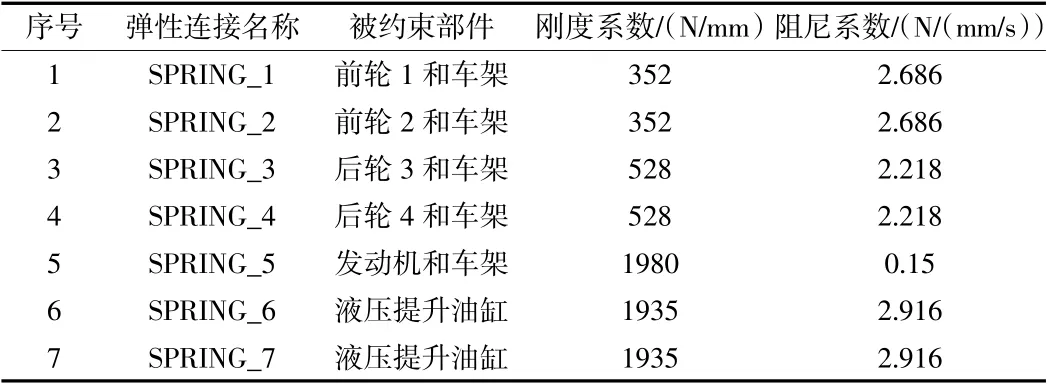
表1 弹性连接

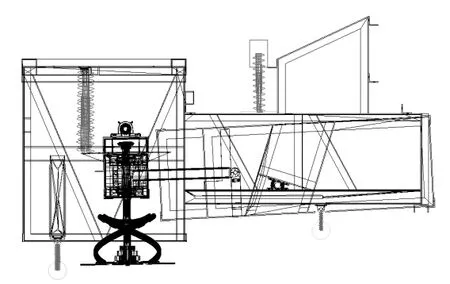
图3 虚拟样机模型

为了模拟甘蔗收获机复杂激励工况，需要在仿真模型中施加路面不平度激励，砍蔗力激励和发动机激励。在车轮弹性连接处设置运动副和路面不平度激振位移驱动，驱动函数为式（1）所示的的位移拟合函数。在发动机质心处施加周期激振力FORCE_1，并由式（2）-（3）定义激振力函数。在切割刀片的切割点位置分别施加径向、切向、轴向切割力，考虑到砍蔗时间约为0.075 s，故可采用ADAMS 内置的step 公式定义三向砍蔗力随时间的变化函数[12]。

3.2 仿真结果分析

只考虑路面激励作用时，发动机激振力和砍蔗力失效，则切割器振动响应如图4（a）所示。由图4（a）可以看出位移响应最大值为1.33 mm，最小值为-3.0 mm，位移的均方根1.356 mm/s，振动速率的均方根值为21.37 mm/s，最大速率为43.96 mm/s。那么在一次砍蔗时间0.0023 s 内刀盘的平均位移和最大位移分别是0.049 mm 和0.101 mm，两次砍蔗间隔时间0.013 s 内刀盘的平均位移和最大位移分别是0.277 mm 和0.571 mm。只考虑发动机激振力作用时，失效路面激励和砍蔗力，切割器振动响应如图4（b）所示，启动平稳后振动具有周期规律性。刀盘位移响应最大值为0.008 mm，最小值为-0.008 mm，均方根是0.0059 mm。振动速率的均方根为1.83 mm/s，最大速率为2.53 mm/s。那么一次砍蔗时间内刀盘的平均位移和最大位移分别是0.0042 mm 和0.0058 mm，两次砍蔗间隔时间内刀盘的平均位移和最大位移分别是0.023 mm 和0.032 mm。只考虑三向砍蔗力作用时，失效路面激励和发动机激振力，切割器振动响应如图4（c）所示，稳定后具有周期规律性。位移响应最大值为0.235 mm，最小值为0.133 mm，均方根是0.192 mm。振动速率的均方根为5.12 mm/s，最大速率为7.98 mm/s。那么一次砍蔗时间内刀盘的平均位移和最大位移分别是0.011 mm 和0.018 mm，两次砍蔗间隔时间内刀盘的平均位移和最大位移分别是0.066 mm 和0.103 mm。相比于发动机激励和砍蔗力激励，路面激励为刀盘振幅的主要激励源。

图4 切割器振动响应

3.3 复杂激励

复杂激励时三种激励共同作用，切割器振动响应如图5 所示。由图5 可知，刀盘位移响应最大值为1.54 mm，最小值为-3.1 mm，均方根是1.501 mm。振动速率的均方根为25.4 mm/s，最大速率为63.6 mm/s。那么一次砍蔗时间内刀盘的平均位移和最大位移分别是0.058 mm 和0.146 mm，两次砍蔗间隔时间内刀盘的平均位移和最大位移分别是0.33 mm 和0.826mm。