线性调频连续波雷达目标参数测量

颜卫忠，陈栋志

(上海航天电子有限公司，上海 201821)

0 引言

线性调频连续波(LFMCW)雷达具有体积小、成本低、分辨率高和不存在距离盲区等优点，在低小慢目标检测[1-3]、汽车防碰撞[4-7]、高精度测量[8-10]和成像[11]等领域有很多应用。

迄今为止，国内外学者对雷达测量目标参数的精度开展了许多研究。Eugin Hyun等[12]基于2D FFT在0.5～3.4 m实现了3 cm的测距精度。国内许多学者基于意形半导体的套片开展了实测，最大可测距离达52 m，测角误差小于0.3°，测速精度小于1 m/s[13-14]。鲍晓丽等人[15]研发了一款24 GHz主动安防雷达，支持距离等参数测量，对人体最远作用距离达77 m[15]。文献[16]基于RFBeam公司的K-MC3 雷达的测速误差小于0.5 m/s，测距误差小于0.6 m。文献[17]基于德国InnoSenT的2款K波段雷达IVQ-905 和RFE3004实现可靠探测距离为60 m，测距误差为0.7 m。文献[18]介绍了一个雷达测速系统，测速误差小于1 km/h，测速范围10～250 km/h。

为实现对道路上不同车道不同目标的雷达监测，需通过实验验证雷达对目标距离、速度及角度的测量精度。为降低实验测试的难度，当前仅考虑单个目标。对于目标角度测量的误差分析，需要保证天线视轴与测角系统中轴线尽可能重合。对于目标速度测量的误差分析主要存在2个问题：① 常规机动目标难以保持匀速运动，而雷达信号处理有一定的延迟；② 市场上的测速仪对最低速度有要求(如>10 km/h)且存在测速误差(<2 km/h)。针对上述问题，本文主要提出了雷达目标测角系统及天线视轴校正方法，校正后天线视轴与测角系统中轴线误差小于1°，通过对电动汽车2个档位的速度进行标定，保证了雷达测速精度估计的准确性。

1 理论模型

雷达发射对称三角形LFMCW信号，经不同目标反射后的回波信号经与发射信号混频得到差拍信号，根据上下扫频的差拍信号信息即可求解目标参数。对称三角形LFMCW雷达收发信号时频关系如图 1所示。图1中，上半部分为三角形发射信号及接收信号的时频关系，实线为发射信号，虚线为回波信号，不同虚线代表不同运动状态的目标，下半部分为差拍信号时频关系，不同状态的目标具有不同的差拍频率。

图1 对称三角形LFMCW雷达发射、接收及差拍信号时频关系Fig.1 Time-frequency relationship diagram of transmitted, received and beat signal in symmetricaltriangle LFMCW radar

目标距离和速度可由差拍频率计算[19]:

(1)

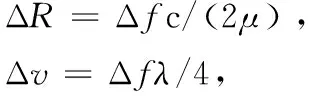
(2)

式中，Δf=fs/NFFT，fs为采样率，NFFT为傅里叶变换点数。

基于单脉冲比相法测量目标的方位角。目标的方位角可以表示为：

(3)

式中，d为2个接收天线间的距离；Δφ表示目标回波在A，B接收天线的相位差：

(4)

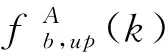
2 实验验证

选用RFbeam公司的24 GHz单发双收雷达传感器K-MC4进行目标参数测量[20]。该雷达最大支持180 MHz调频带宽，天线波束覆盖范围±15°，2路I/Q输出。雷达输出的差拍信号经滤波放大及数字信号处理后，测量结果在上位机显示。雷达参数如表 1所示。下面分别对目标距离、角度和速度3种参数进行实验测量，验证测量误差。

表1 雷达参数Tab.1 Radar parameters

2.1 距离测量

首先，将雷达用三脚架固定，在距离雷达一定距离处放置一个支架，将一块23 cm×60 cm的不锈钢平板垂直固定在支架上，如图2所示。目标距离分辨率可以表示为：

(5)

图2 目标距离测量场景Fig.2 Target range measurement scenario

式中，N为半周期采样点数，N=fs×T/2。由表 1可得距离分辨率ΔR=0.488 m。由于栅栏效应，雷达测量距离与实际距离最大误差为±0.244 m。

将平板放置在距离雷达的4个不同距离处，雷达回波信号经傅里叶变换后的频谱如图 3所示。4次距离测量结果如表 2所示。可以发现，距离测量误差最大为0.29 m，略大于理论误差最大值0.244 m。这可能有2个原因：① 平板容易被风吹动，与实际距离有微小差异；② 雷达实际产生的调频带宽可能小于理论值，这将导致距离分辨率变大，进而导致测距误差变大。为解决上述问题，可取多次测量结果以及通过固定距离目标对雷达带宽进行校正。

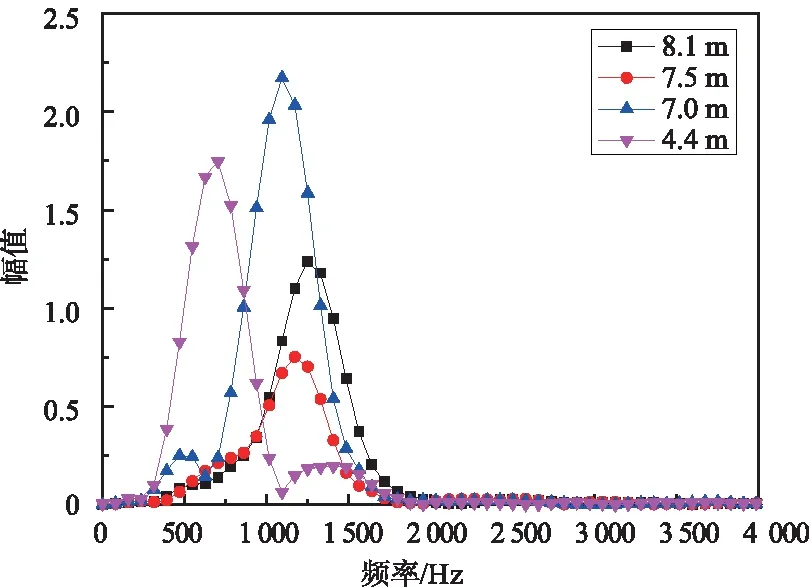
图3 目标回波频谱图Fig.3 The spectrogram of target echo

表2 距离测量误差分析Tab.2 Range measurement error analysis

2.2 角度测量

接下来，验证雷达测量目标角度的误差，步骤如下：

① 架设雷达并确定测量系统各参考线。为便于角度调整，将雷达固定在转台上，天线阵面与转台垂直，转台固定于三脚架上。首先，确定雷达的中轴线，然后确定相对中轴线的各角度标记线。这里规定从中轴线顺时针旋转为正，逆时针旋转为负。雷达测量目标角度的示意如图 4所示。

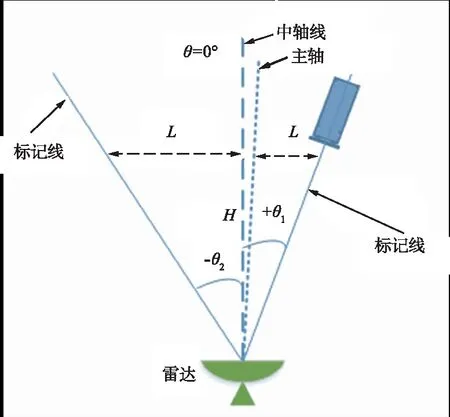
图4 目标角度测量示意Fig.4 Schematic diagram of target angle measurement

② 对天线指向进行校准。在角度测量系统的中轴线上放置定标体，不断调整天线指向并测量定标体的角度，使定标体的角度小于阈值δ，定标体的角度记为θT。雷达天线指向校准步骤为：首次测量系统中轴线上的目标角度θ0，若目标角度小于阈值δ，即|θ0|<δ，则无需校正。否则，当θ0>0，则雷达天线需顺时针转，反之，雷达天线逆时针转。天线固定后，再次测量目标角度θ1。如此反复调整天线指向，直至|θi|<δ，则校准完成，且天线主轴方向记为θT=θi。其中，角度校正误差阈值δ需根据测角精度来设置。

③ 将目标放置在雷达波束范围内的任意角度的标记线上，利用雷达测量目标的角度。

④ 结果处理及分析。

分别选取了±9°，±7°，±5°，±3°设置标记线，然后将角反射器依次放在各标记线上，测角实验如图5所示。设置误差阈值δ=1°。雷达对不同角度目标进行测量，每一个角度均测量一组数据，测量结果如图6所示，图中虚线区域表示目标实际角度偏差±1°。可以发现测角偏差基本小于1°，这与阈值(δ=1°)相符合，如果进一步降低δ，则测角误差有望进一步降低。表 3给出了角度测量均方根误差，各个角度均小于0.35°。

图5 目标角度测量实验Fig.5 Target angle measurement experiment

表3 角度测量误差分析Tab.3 Angle measurement error analysis 单位：(°)

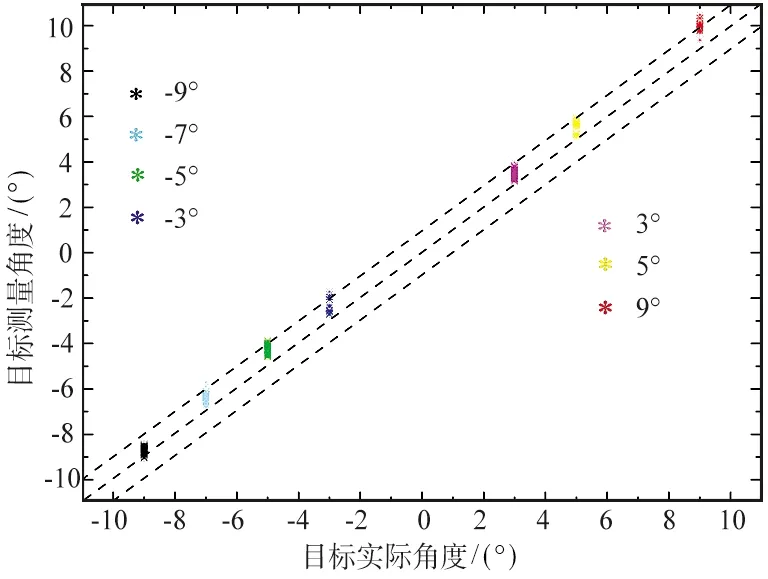
图6 目标角度测量结果Fig.6 Results of target angle measurement

2.3 测速精度

表4 电动车平均速度测量Tab.4 Average speed measurement of electric vehicle

图 7给出了玩具电动车速度的雷达测量结果，电动车先按照1档速度运动(区域①)，后按2档速度运动(区域②)。由图7可以看出，电动车在每个区域基本以匀速运动，区域②的距离曲线的斜率大于区域①，即速度变大了。雷达测量目标速度主要有3个值，分别是-0.732，-0.488，-0.976 m/s。

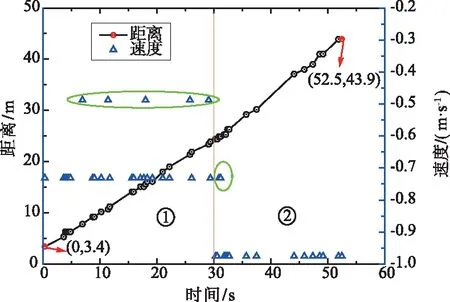
图7 目标速度测量结果Fig.7 Target velocity measurement result

表5对速度测量误差进行了分析。可以看出，区域①和②的雷达测量平均速度与实际平均速度的相对误差分别为0.85%和2.34%。而雷达瞬时测速结果误差较大(3.1%和8.57%)，这主要有2个原因：① 雷达信号处理速度分辨率太大。由式(2)可知，速度分辨率Δv=Δfλ/4=0.243 m/s，则最大速度误差为Δv/2=0.12 m/s；② 目标速度太小。随着目标速度的提高，速度相对误差将不断降低。此外，图6中弧形区域的速度与目标实际速度相差较大，这主要是由于电动车在行进过程中偏离雷达天线视轴后人为调整方向，导致径向速度的降低。

表 5 速度测量误差分析Tab.5 Velocity measurement error analysis

3 结束语

针对线性调频连续波雷达测量目标参数的误差估计问题，提出了角度测量系统校正方法以及针对运动目标的平均速度误差估计方法。利用线性调频连续波雷达对目标距离、角度和速度3个参数进行了实验测量。在当前实验条件下，测距误差小于0.3 m，测速误差小于0.5 km/h，测角平均误差小于1°。目前，国外主要针对77，94 GHz甚至更高频率的雷达及信号处理进行研究，此类雷达能够将测距、测速精度提高10倍，为姿态感知、高精度测距和自动驾驶提供支持。未来，将采用更大带宽以实现更高精度的参数测量及态势感知。