基于独立分量分离的雷达通信一体化接收算法

荆春晖，郭文彬

(北京邮电大学 信息与通信工程学院，北京100876)

0 引言

雷达通信一体化理论近几年来得到广泛研究，其中波形设计方向研究众多，但在接收端信号分离部分研究甚少，接收端的合理设计能够确保信号的有效接收分离，以便信息的提取及应用，本文在选用合理的波形设计前提下，将信号分离作为研究重点。

在一体化信号的设计中，信号共享设计目前主要研究分2个方向，一是基于通信信号，对通信信号进行改进实现雷达探测功能。其中正交频分复用(OFDM)信号应用较为广泛[1]，但是OFDM系统中峰均功率比过高问题始终影响整个系统的性能，波形失真以及传输功率降低的问题十分显著[2]。为了实现高效率的通信传输，Anderson等人[3]提出了连续相位调制(CPM)的恒定包络的通信方案，其连续相位特征可提高频谱效率，恒定包络的特性可以抵抗发射机中非线性组件引入的失真的鲁棒性，其中矩形滤波下的全响应连续相位调制即为CPFSK[4]，因其结构简单近年来得到广泛关注与应用。

基于雷达信号，将通信信息嵌入雷达波形中，同样可以实现信号的一体化。在文献[5]中，利用线性调频信号(LFM)的新型雷达与通信集成，实现稳定通信与雷达探测，但是由于LFM雷达与通信结合后的低容量无法满足高速率传输的需求。调频连续波FMCW雷达分辨率高、无测量盲区同样得到广泛应用，文献[6]将CPM与FMCW结合，提出了相位连接雷达通信(PARC)框架，可以最大化数据吞吐量和目标能量，但是由于雷达通信未能准确分离而引发距离旁瓣调制(RSM)导致的多普勒扩展杂波。因此接收端通信雷达信号的分离尤为重要。

当前的理论研究大部分假设接收端已知雷达信号，将接收信号与雷达信号共轭相乘即可得出通信分量，未能真正实现信号未知情况下的信号分离。结合实际环境，在接收端未知信号相关参数、时域频域分离信号困难的情况下，本文从盲源分离的角度实现一体化信号的有效分离。1991年，Jutten对独立分量分离(ICA)进行了数学阐述[7]，采用神经网络算法处理盲源分离问题。1995年，盲源分离将代价函数与神经网络相结合成功分离语音信号，并引入信息论，证实了ICA算法的简单高效[8]，在后期的研究中，盲源分离大部分采用ICA算法，很多文献将盲源分离与ICA不加区分。ICA算法利用源信号的独立性假设，结合雷达通信一体化信号的复数性质，本文采用复值的ICA算法分离。

复值独立分量分离算法分为2类，一类基于统计特性精确求解，较为典型的复值联合近似对角化(JADE)算法[9]将实值JADE算法中矩阵的转置运算转变为共轭运算，算法实现简单，分离效果好，但是随着信源数目的增加，算法复杂度会增大[10]；一类基于非线性函数，利用高阶统计特性近似处理，其中复值快速不动点(FastICA)算法包括基于最大负熵、峭度、极大似然等类型[11]，只对信号的幅值运算，未考虑信号的相位[12]，只有当信号满足球对称性时，才能保证信号的分离效果。CMN算法[13]采用负熵最大化的准则来衡量信源的非高斯性，使用复解析函数来近似匹配信源的概率密度，同时考虑相位及幅值因素，能够更加有效地分离信号。

为了实现雷达探测的准确性以及通信的可靠性与高效性，本文将通信序列经过CPFSK调制后嵌入FMCW雷达信号中，实现雷达通信一体化。结合一体化信号波形的特性及分离算法性能对比，本文采用CMN及JADE的复值独立分量分离算法分离通信与雷达信号，同时在分离算法前增加小波去噪及预处理模块，提升信号分离的有效性。分离后的通信分量进入通信接收机，采用Viterbi译码方法提取通信分量；雷达分量形成回波返回雷达接收机，对雷达信号进行动目标检测技术实现雷达的距离和速度探测。

1 基于CPFSK-FMCW的雷达通信一体化系统

CPFSK-FMCW雷达通信一体发射机如图1所示。通信符号序列经过预编码后进行CPFSK调制形成通信分量，线性调频序列形成FMCW信号与通信分量相乘，形成CPFSK-FMCW一体化信号，一体化信号经过中心载波Acos(ω0t)调制后发射。

图1 CPFSK-FMCW雷达通信一体化发射机Fig.1 CPFSK-FMCW radar communication integrated transmitter

CPFSK-FMCW联合波形定义为：

(1)

雷达部分采用锯齿波成形的FMCW信号，持续时间Tchirp内的第i次扫描为：

Sr(t)=exp(j2πψr(t-iTchirp))，

(2)

通信部分采用CPFSK调制后的通信信号，表示为：

Sc(t;I)=exp(j2πψc(t;I))，

(3)

2 基于独立分量分离的联合接收算法

传统的雷达通信一体化信号接收机部分，假设已知雷达信号[14]，对接收到的一体化信号与雷达信号的共轭相乘即可得出传输的通信信号，但这种方案无法处理接收端雷达信号未知的情景，由此，本文引入盲源分离的思想处理未知信号的分离。

本文提出的一体化信号为雷达信号与通信信号的乘积，乘性信号的分离较为复杂，对式(1)进行对数运算即可变为加性信号，对加性信号的分离方法多且简单有效，结合盲源分离的常用算法以及一体化信号的复数性质，本文采用盲源分离中基于独立分量复信号分离的方案。

复数ICA模型可表示为：

z=As+N，

(4)

式中，s=[s1(t;I),s2(t;I),…,sn(t;I)]T为n个源信号；A为M×N混合复矩阵且列满秩；z=[z1(t;I),z2(t;I),,zm(t;I)]为m个观测信号；N为零均值高斯随机噪声向量。

ICA算法的目的是构造一个分离矩阵w，从观测信号中恢复出源信号，解混模型为：

r=wz≈s，

(5)

式中，r=[r1(t;I),r2(t;I),…,rn(t;I)]是分离系统的输出，即源信号的估计。

传统的复值ICA算法不考虑噪声的影响，为了所设计的系统更加贴合实际环境的需求，本文考虑噪声存在的环境，增加预处理模块，首先对接收信号解调至基带信号y(t;I)，利用小波变换进行软门限降噪以及中心化、白化处理，然后进行复值ICA算法分离信号，改进的接收机处理系统如图2所示，由于CMN算法及JADE算法代表复值ICA算法2种不同分离形式，二者分别加入系统中，构造出分离矩阵，对比验证对信号分离的有效性。

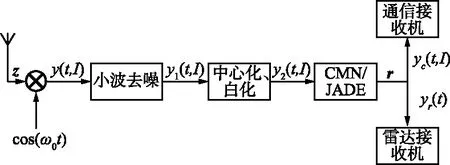
图2 CPFSK-FMCW雷达通信一体化接收机Fig.2 CPFSK-FMCW radar communication integrated receiver

2.1 预处理

本文采用小波变换对接收信号进行软门限降噪[15]，具体步骤如下：

① 小波分解：选定恰当的小波基及分解层数，对基带信号进行小波分解，得到小波分解系数；

② 软阈值处理：对小波分解系数进行软阈值量化处理，得到各层估计小波系数；

③ 小波重构：利用估计的小波系数进行小波重构，重建原始信号[16]。

经过小波去噪后的信号y1(t;I)在进行盲分离前还需要进行中心化和白化处理，以提高算法的收敛性和降低信息的冗余[17]。复值信号经过白化处理后，分离矩阵一般为酉矩阵，提高算法收敛性的同时减少计算量。对y1(t;I)协方差矩阵Ryy特征值分解得：

Ryy=E{y1(t;I)y1(t;I)H}=UΣUH，

(6)

式中，U为正交矩阵；Σ为特征值对角阵。则白化矩阵为V=Σ-1/2UH，将去噪后的信号与白化矩阵相乘，可得到预处理后的信号y2(t;I)。

2.2 非高斯最大化算法原理

CMN算法的代价函数为[18]：

J(w)=E{|G(wHy2(t;I))|2} ，

(7)

式中，G为光滑的非线性函数；w为分离矩阵的一列，满足约束条件‖w‖=1。

此代价函数比复值FastICA算法中的代价函数增加了相位信息，从而可以更加灵活地对信源的概率密度进行匹配。

在约束条件下，通过极大化J确定一个最优的w，从而估计出一个独立分量。CMN代价函数的优化便可转化为以下的约束：

(8)

采用牛顿法，可得出分离矩阵每一列更新表达式：

w(m+1)=-E{G*(x)g(x)y2(t;I)}+E{g*(x)g(x)}w(m)+

E{y2(t;I)y2(t;I)T}E{G*(x)g′(x)}w(m)*,

(9)

式中，x=w(m)Hy2(t;I)；m为迭代次数；g为G的一阶导数；g′为G的二阶导数。

式(9)只针对单一信源，对所有信源的分离，需要对分离矩阵的每一列进行更新。下面给出了CMN算法的具体流程：

① 对经过小波去噪的信号进行中心化和白化处理，得到预处理后的数据y2(t;I)；

② 分离矩阵初始化W(0)=IN，IN为N×N维单位矩阵。同时设定最大迭代次数mmax和允许误差ε；

③ 对W(m)中每一列按照式(9)迭代更新，得到W(m+1)；

④ 正交化分离矩阵；

⑤ 当‖|W(m)HW(m+1)|-IN‖F<ε或m+1=mmax时，停止迭代，此时W=W(m+1)；否则令m=m+1返回步骤③。其中‖·‖F表示Frobinius范数。

2.3 联合近似对角化算法原理

JADE算法构造多个四阶累积量矩阵，通过联合对角化求解分离矩阵[19]，进而对信号进行分离。

对任意一个N×N矩阵M，构造经过预处理后信号y2(t;I)的四阶累积量矩阵：

(10)

式中，y2i(t;I),y2j(t;I),y2k(t;I),y2l(t;I)为y2(t;I)的第i,j,k,l个元素；qij为矩阵Qy2(t;I)(M)中第i行j列元素；mlk为矩阵M第l行k列元素。

综合考虑高阶累积量的特性及ICA算法中的白化矩阵特点，可以证明四阶累积量矩阵为对角矩阵：

Qy2(t;I)(M)=VQz(M)VH=VAQs(M)(VA)H=

UQs(M)UH=UΛUH,

(11)

式中，U为酉矩阵，通过对Qy2(t;I)(M)进行联合对角化即可得出U的估计值。最终分离矩阵为UHV。信号分离后，接收机可分为通信和雷达两部分，分别进行通信信息的提取以及雷达的距离速度检测。

2.4 通信接收机

接收信号通过上述算法分离后，即可得到通信信号：

yc(t;I)≈exp(j2πψc(t;I))。

(12)

将yc(t;I)与参考信号sref(t)混合，带宽降低的同时，将信号下变频至中频信号，并进行带通滤波。中频信号表示为：

yIF(t;I)=ΦBPF{yc(t;I)×sref(t)}，

(13)

式中，ΦBPF{·}为带通滤波器。然后将中频信号混频为基带信号并进行IQ解调得到复数信号：

yI(t;I)+jyQ(t;I)=ΦLPF{yIF(t;I)×exp(-j2πfct)}，

(14)

式中，ΦLPF{·}为低通滤波器；yI(t;I)和yQ(t;I)分别为复数信号的同相和正交相分量。接着对2分量分别进行附加增量计算，得到增量，进而对增量采用Viterbi算法[20]，实现CPFSK解调，恢复发送的通信原始序列I′=[I′1,I′2,...,I′n]。

2.5 雷达接收机

本文采用距离多普勒处理从分离后的雷达信号中提取雷达目标信息。分离后的雷达信号表示为：

yr(t)≈exp(j2πψr(t-iTchirp))。

(15)

首先采用类似的二维傅里叶变换方法进行雷达部分处理，对接收到的反射信号中雷达信号与来自本地振荡器的雷达信号波形混合并进行频差检测。混合后的信号经过去毛刺后可表示为：

yrf(t)=exp(j2π(ψr(t-τ-iTchirp)-ψr(t-iTchirp)))。

(16)

对于距离为R和速度为v的目标反射，延迟时间τ=2(R-vt)/c，频差可表示为：

ψr(t-τ-iTchirp)-ψr(t-iTchirp)=f0τ0+(fr+fd)(t-iTchirp)+ifdTchirp,

(17)

式中，τ0=2R/c;fr=k·2R/c;fd=f0·2v/c。

根据式(17)可以看出,差频信号中包含目标的距离和多普勒信息，采用二维傅里叶变换即可获取[21]。

3 仿真与系统验证

根据所设计场景，对雷达通信一体化系统进行建模仿真，通过分离效果检测分析分离系统的可靠性，通过动目标检测验证雷达的测速测距性能。

3.1 分离效果检测

复数ICA算法分离性能通常采用Amari指数衡量，定义为[22]：

(18)

式中，P=WHVA，W为白化后的分离矩阵，V为白化矩阵，A为混合矩阵;N为信源数目。性能指标IA总是非负的，越接近零表示分离误差越小，分离效果越好。

为了研究CMN算法、JADE算法及小波去噪算法对系统分离效果的影响，采用4种方案对雷达通信一体化信号进行分离。在高斯白噪声的信道下，分别单独采用CMN算法、JADE算法进行信号分离；然后结合小波去噪，分别采用小波去噪联合CMN算法、小波去噪联合JADE算法，其中选用小波基“bior5.5”，小波分解层数为2的小波进行软阈值去噪处理。雷达初始频率f0=3.85 GHz，调频带宽B=150 MHz，Tchirp=160 μs，选用码元速率为RB=0.8 MBaud/s的二进制通信符号序列，调制指数h=0.25。

图3、图4给出雷达通信一体化混合信号以及各方案分离信号的星座图。

(a)雷达通信一体化信号

(b)分离后雷达信号

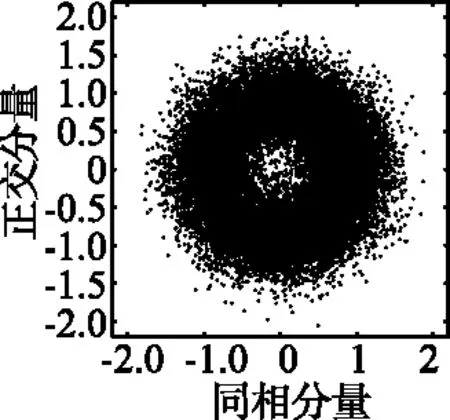
(c)分离后通信信号图3 CMN算法星座图Fig.3 CMN algorithm constellation

(a)雷达通信一体化信号

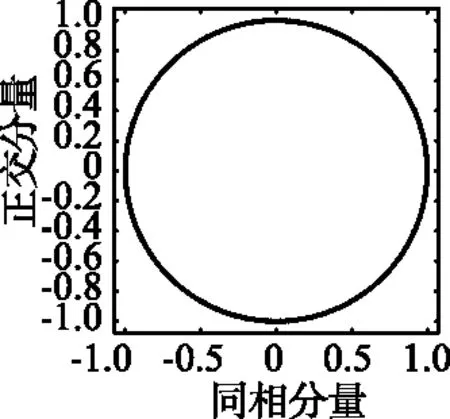
(b)分离后雷达信号

(c)分离后通信信号图4 小波去噪联合CMN算法星座图Fig.4 Wavelet denoising combined CMN algorithm constellation

JADE算法、小波去噪联合JADE算法星座图与图3、图4基本一致，此处不再赘述。从分离后的星座图可以看出，FMCW信号分离不受噪声影响，CPFSK信号的分离采用小波去噪联合CMN算法/小波去噪联合JADE算法比单独使用CMN/JADE算法效果更好。噪声的存在对通信信号引入强烈的非线性，小波去噪能有效缓解非线性的干扰，促使分离性能提升。

为了更加精确验证4种方案分离性能，测试在不同的比特信噪比情况下，通信信号增加不同程度的高斯白噪声，采用上述4种方案进行信号分离实验，计算出不同信噪比条件下不同方案的分离性能指标IA的变化曲线，如图5所示。

图5 不同方案分离性能指标曲线Fig.5 Separation performance index curves of different solutions

由图5可以看出，分离性能指标范围位于(0,1)中，表明分离效果满足理论分离指标要求。随着比特信噪比的增加，整体的性能指标呈下降趋势，即分离效果越来越好。4种方案中，增加了小波去噪的算法分离效果比单独使用独立分量分离算法更好，JADE算法性能整体比CMN算法效果好，对于本文所设计的一体化系统，小波去噪联合JADE算法更加适合。

3.2 动目标检测

雷达接收端对分离后的雷达信号进行差频检测，仿真中码片数为128，扫描周期数为1 024，初始频率f0=3.85 GHz，调频带宽B=150 MHz。根据可探测的最大距离转化为时间得到最大延时，设定最大延时2倍为雷达一次扫描时间，Tchirp=160 μs。假设目标距离雷达R=300 m，速度v=50 m/s，仿真结果如图6、图7、图8所示。

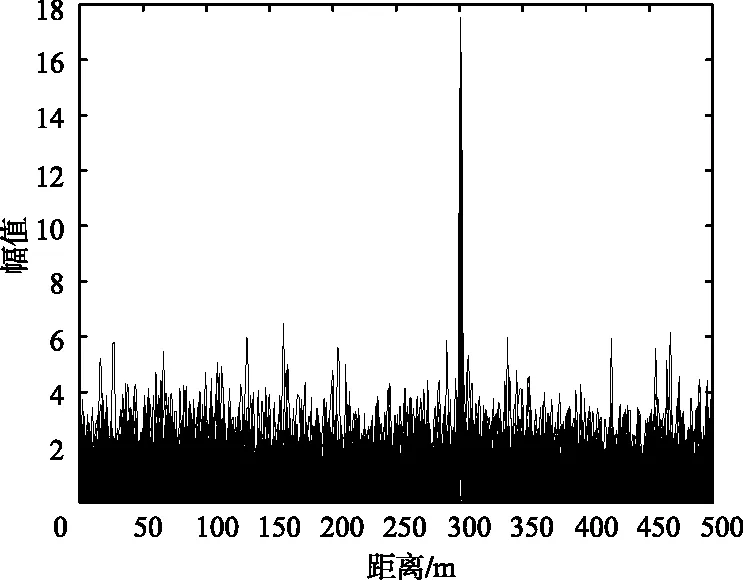
图6 第一次FFT后距离功率谱密度周期图Fig.6 Range power spectral density periodogram after first FFT

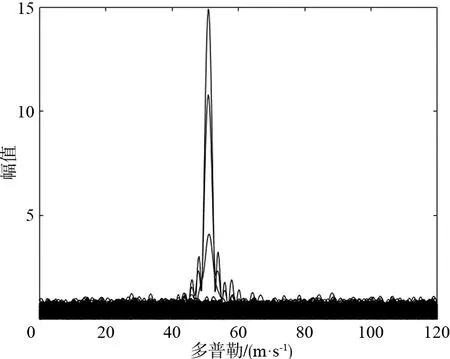
图7 第二次FFT后的多普勒功率谱密度周期图Fig.7 Doppler power spectral density periodogram after second FFT

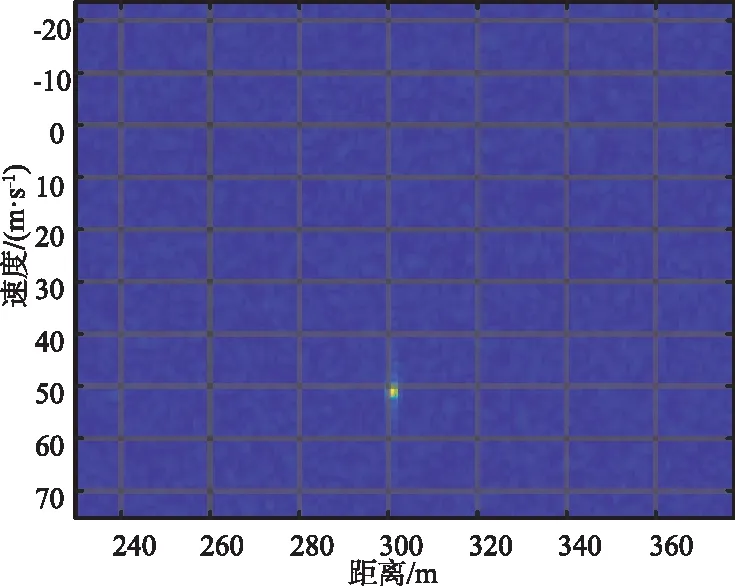
图8 距离多普勒响应Fig.8 Range Doppler response

图6为1 024个扫描周期中经过第一次FFT变换后得到的距离功率谱密度周期幅度图。图7为1 024个扫描周期中经过第二次FFT变换后得到的多普勒功率谱密度周期幅度图，根据幅度最大值得位置可以准确判断目标的距离及速度。图8为距离多普勒响应，可以看出经过一体化结合又分离后的雷达信号探测性能正常，未受到杂波的影响，可以实现目标的距离和速度探测。

4 结束语

本文将CPFSK调制后的通信序列嵌入FMCW雷达信号中，实现雷达通信的一体化传输，接收端采用小波去噪联合CMN算法及小波去噪联合JADE算法有效分离2种信号，分别设计相应的接收机处理，选取合理的雷达通信参数，实现雷达有效探测的同时通信信息的可靠传输。仿真结果表明，本文所设计的一体化信号及接收机分离系统能够有效实现嵌入通信信号的雷达信号的传输与信息提取。在信源数目较少的情况下，本文提出的小波去噪联合JADE算法更能精确分离一体化信号。