基于改进型BP神经网络的大型CCHP系统负荷预测研究
2021-03-16国网上海市电力公司闸北发电厂顾兆雄黄志坚
国网上海市电力公司闸北发电厂 顾兆雄 黄志坚 谢 鸣
上海海事大学 林萌雅 齐家业 高文忠△
0 引言
随着我国经济的迅速发展,全社会整体空调能耗急剧增加,在夏季,空调耗电量已占到居民用电量的40%~50%左右,对雾霾“贡献”显著。近年来,特别是在“十三五”规划政策的大力推动下,推进能源革命,发展绿色能源,建设清洁低碳、能源可持续发展和节约能源的现代能源体系[1]已取得全社会的共识。其中CCHP(combined cooling heating and power)系统(又称冷热电联产系统)得到快速发展,其总能源利用率可以达到75%~90%,是能源综合梯级利用的有效解决方案。
大型CCHP系统通常使用清洁能源天然气作为主要一次能源,在综合考虑初投资、装机容量和运行经济性的基础上,常配置一定容量的电制冷机和蓄能储罐,既可利用电力谷价蓄冷降低成本,亦可调节负荷。其供冷主体主要有3种,即溴化锂制冷机、电制冷机和蓄冷罐。其中,溴化锂制冷机由内燃机余热驱动,能量来自天然气,电制冷机组由电力驱动,该电力首先使用内燃机自发电,不足部分购买市政电力,而市政电力存在峰时、平时和谷时电价,且因季节差异而不同。蓄冷罐兼顾谷电蓄冷和调节作用。因此,在如此复杂的供能体系和价格体系下,只有准确预知第2天的负荷值和变化趋势,才能依据该结果通过具有智能化的控制系统,调配各供能主体运行台数和时间,获得系统运行整体的最优化,包括经济最优、能耗最优和碳排放最优等方面。
一般建筑物的空调冷负荷受气象参数、季节、建筑性质和投用阶段等多种因素影响,存在复杂的非线性关系,利用建筑设计阶段的负荷计算方法难以预知第2天的负荷。近十几年来,众多专家学者针对空调负荷的特点,从运行数据角度提出了一些预测方法。主要有人工神经网络法(ANN)、多元非线性回归法(MNLR)、支持向量回归法(SVR)及时间序列法等[2]。
多元非线性回归法简单易理解,但其通用性差。时间序列法预测速度快,通常用于短期预测,如未来数小时的预测,但模型不能充分利用负荷的影响因素,只适用于负荷变化均匀的短期预测。与其他方法相比,人工神经网络法的优势在于能够对变量之间复杂关系给出的多变量问题进行建模,并通过训练数据的“学习”来提取这些变量之间的隐含非线性关系。近些年来,运用人工神经网络预测负荷得到了一定的发展。如Zhou等人通过对大型商场空调负荷预测的应用,阐述了4种不同的基于机器学习的预测方法,并对它们的预测性能进行了比较[3]。Ling应用BP神经网络-马尔可夫预测模型进行热负荷预测,不仅发挥了BP神经网络预测精度高的特点,而且能够利用马尔可夫模型对波动数据进行较精确预测[4]。Liao采用改进的差分进化算法优化小波神经网络的权阈值,并与传统算法优化神经网络进行了比较[5]。Solmaz等人利用人工神经网络方法来预测汽车小时冷负荷,通过对7~40个隐层神经元数目的逐步检测,寻找最匹配的神经网络结构[6]。Ding等人将输入变量随机形成8个组合,分析各种输入变量对预测精度的影响,利用人工神经网络和支持向量机模型进行预测精度比较[7]。
相对以上研究中的小型空调系统,大型CCHP系统的用户建筑规模通常比较庞大,主要以区域供冷供热为典型特征,建筑类型涉及办公建筑、公寓、酒店等多种形式,虽然每种建筑类型的日、月和季节负荷特征变化规律存在明显差异,但其耦合性却非常显著,往往表现出与气候特征较密切的关联性。基于此,笔者尝试利用人工神经网络的GA-BP模型,结合Speaman秩相关系数对大型CCHP系统的负荷影响因素进行分析,以期利用建筑负荷耦合特征,获得更准确的针对大型CCHP系统空调负荷的预测方法,为此类系统的智能优化运行提供更精确的数据支撑。
1 BP神经网络预测模型的优化改进
BP神经网络是一种典型的递归网络,由输入层、隐含层和输出层构成[8],具有非线性映射能力及强大的学习能力,对规律较复杂、非线性关系的数据具有良好的分析和处理能力[9],且具有信息记忆、自主学习和优化计算的特点[10]。但也存在局限性,即:1) 学习速度慢、维数灾难;2) 很容易陷入局部收敛,无法保证全局收敛最优解;3) 难以科学地确定网络结构。其中,网络结构及输入参数的选取对模型的学习速度和结果存在明显影响,目前多凭经验确定隐含层节点数。
为了解决学习速度慢、维数灾难的问题,首先尝试引入Spearman秩相关系数对影响负荷预测的因素作相关性分析,然后选取相关性较高的影响因素作为输入变量。相对于全部影响因素作为输入变量,运用Spearman秩相关系数选取输入变量,起到降维的作用,从而提高训练速度,增加模型的适用性。Spearman秩相关系数的优势在于,它用来衡量2个变量之间的关联程度与方向,对原始变量分布不作要求,属于非参数统计方法。在满足没有重复数据的情况下,若2个变量间为严格单调函数关系,则Spearman秩相关系数就是1或-1,则称2个变量完全Spearman秩相关。2个变量的Spearman秩相关系数越大,则两者的相关性越大。该方法可用于输入与输出变量间关联程度的分析,避免输入变量过多或人为排除重要的变量,选出相关程度较高的变量。其计算步骤为:1) 将2个列向量X和Y对应的元素xi、yi转换为在各自列向量中的排名,记为x′i、y′i。2) 根据式(1)计算Spearman秩相关系数。
(1)
式中rs为Spearman秩相关系数;n为样本数量;di为秩次差,di=x′i-y′i。
针对BP神经网络很容易陷入局部收敛、无法保证收敛全局最优点的缺陷,采用将其与具有全局搜索能力的遗传算法相结合,从而使神经网络的初始权值和阈值得到优化,进而优化整个网络结构,构成兼顾两者优点的GA-BP神经网络预测模型。其算法结构流程如图1所示。

图1 GA-BP算法的流程图
GA-BP神经网络训练首先对经过Spearman秩相关系数确定的输入参数及其构成的数据集进行训练,然后通过遗传算法具有的选择、交叉与变异操作,在生成的新一代种群中寻找满足适应度条件的个体,从而得到BP神经网络的最佳初始权值与阈值;接着BP神经网络算法以遗传算法提供的最优初始权值和阈值开始训练过程,最后逼近最优解[11]。具体步骤如下:
1) 根据神经网络拓扑结构对初始值进行编码,生成初始群体。
2) 使用初始值训练神经网络。
3) 通过训练结果,计算每个个体的适应度值,筛选出最佳的适应度的个体进行下一代计算。
4) 对筛选出的群体进行选择、交叉和变异等遗传操作,生成一代新的群体。
5) 重复步骤2)~4),直至满足适应度条件,获取最优的权值和阈值。
6) 使用经过遗传算法优化的权值与阈值进行训练,得到结果。
2 原始数据处理和负荷预测模型构建
选取位于上海浦东新区某区域供冷/热的大型CCHP系统为研究对象,该能源中心主要为28栋办公楼及附属商业建筑供能。其供能总面积为647 000 m2,夏季设计日逐时冷负荷峰值为56.8 MW,日总供冷量为660.9 MW·h,冬季设计日逐时热负荷峰值为34.3 MW,日总供热量为441.6 MW·h。整个CCHP系统主要由2台内燃机、2台烟气热水型双效溴化锂机组、6台离心式电制冷机组、3台燃气热水锅炉及蓄能罐组成。其中溴化锂机组的额定制冷功率为4 105 kW,电制冷机组的额定制冷功率为7 000 kW,蓄能罐的蓄冷量为51 502 kW·h,蓄热量为35 000 kW·h。能源系统原理如图2所示[12]。该系统于2016年投入使用,2018年夏季典型日的最大逐时冷负荷为22.5 MW,总供冷量为239.3 MW·h,典型日负荷分布如图3所示。鉴于该能源中心具备较完善的运行数据采集和存储系统,选取2018年7月2日至10月8日(06:00—18:00)的工作日(非工作日负荷极小,忽略)逐时负荷和当地气象局发布的气象数据,利用构建的BP和GA-BP神经网络分别进行机器学习,分析其内在关系。然后对选取日的空调负荷进行预测。
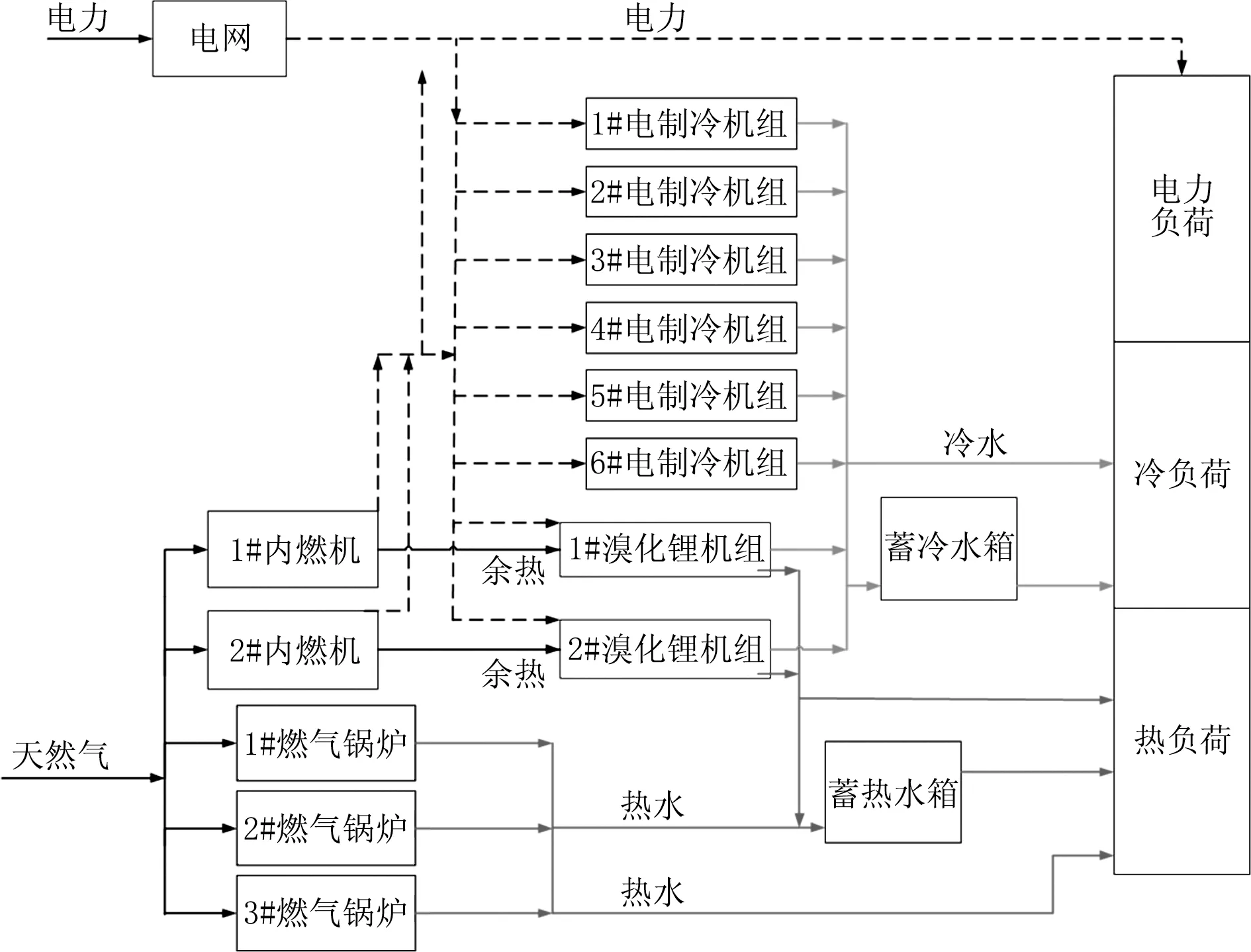
图2 系统原理图
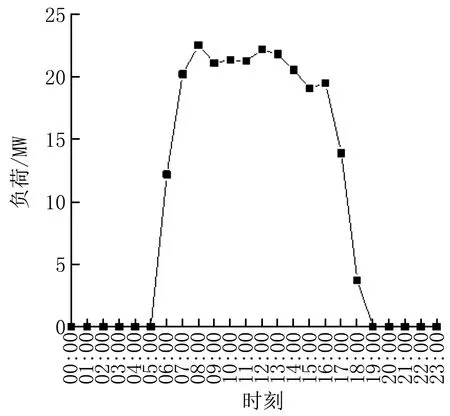
图3 典型日负荷分布
2.1 原始数据处理
空调负荷预测精度主要受数据集质量及模型可用性影响,为提高预测模型精度,对原始数据集进行清洗和处理是关键一步。在能源中心数据采集过程中,可能存在设备调试、断电及网络传输故障等各种干扰,使得少量原始数据出现异常,远远偏离正常水平,剔除异常值有助于提高模型预测的精度。
能源中心供冷时间段为非节假日的06:00—18:00,该时间段内冷负荷为0的值视为异常值。另外,非节假日负荷变化趋势具有相似性,如果某时段负荷值突然远大于或远小于对应时刻附近的负荷值也视为异常值。依此将日供冷时间按时段分为13个时序,通过图示法找出异常值,异常值分布如图4所示。
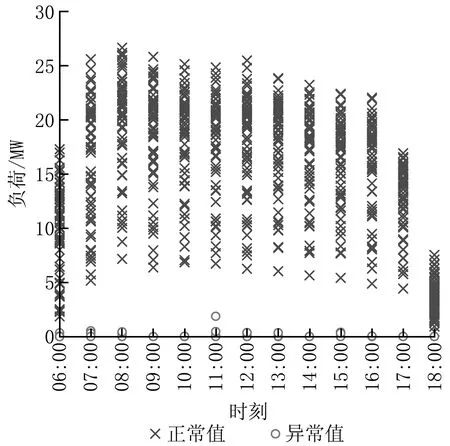
图4 异常值分布
为了避免量纲及数值间差异带来的影响,需要对数据进行归一化处理[13]。模型采用的数据集由逐时冷负荷与逐时气象参数组成,两者的量纲及数值间存在差异。因此,将剔除异常值后的数据集进行归一化处理。即采用最常用的方法:零-均值规范化。经过零-均值规范化处理后的数据均值为0,标准差为1。其处理公式为
(2)

2.2 负荷预测模型的构建
空调负荷影响因素主要有建筑物内扰(如室内人员数量、散热设备使用频率与室内温湿度等)和建筑物外扰(如室外气象参数(温度、湿度、辐射、风速和天气等))[14]。考虑到太阳辐射及室外温度会造成空调冷负荷滞后影响,因此,在模型中加入了(T-1)时刻的温度及湿度影响因素[15]。另外因无法获取建筑物内扰作为变量,但鉴于空调冷负荷存在时间序列性,将(T-1)时刻冷负荷、(T-2)时刻冷负荷、(T-24)时刻的冷负荷作为模型的输入参数,间接实现了内扰的输入,提高预测精度[16]。
为了提高模型学习速度、弱化维数灾难,提高负荷预测模型精度,通过式(1)分别对上述各影响因素与负荷作相关性分析,获得各影响因素与冷负荷的Spearman秩相关系数,具体结果见表1。

表1 影响因素与冷负荷的Spearman秩相关系数
通过表1中数据可以看出:1) (T-1)时刻与T时刻的冷负荷的秩相关系数最高,为0.810 6,说明空调冷负荷时间序列性很强;2) (T-24)时刻与T时刻的冷负荷的秩相关系数为0.573 0,主要是这两日的气象参数存在较大差异,造成负荷存在差异;3)T时刻室外风向和风速的Spearman秩相关系数分别只有0.121 0、0.102 7,这与供冷对象为全封闭外围护建筑结构,无自然通风有关。综合表1中所有数据,选取(T-1)时刻冷负荷、T时刻室外空气温度、(T-1)时刻室外空气温度、(T-2)时刻冷负荷、(T-24)时刻冷负荷和T时刻室外相对湿度作为输入参数。
为了改善BP神经网络预测模型易陷入局部收敛,将预处理后的数据利用遗传算法进行初始权值和阈值寻优,获得最优初始权值与阈值,以最优初始权值和阈值开始训练过程,最后逼近最优解。采用的3层GA-BP神经网络结构如下:
1) 输入层的设计。将上述6个影响因素作为输入参数,则输入变量为6维向量。
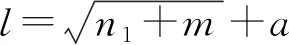
3) 输出层设计。根据对输入参数的训练学习,预测空调冷负荷作为输出层节点。最后构造一个6-11-1型的GA-BP神经网络结构。
2.3 模型精度评价指标
选用期望误差百分比PEE及平均绝对误差EMB作为负荷预测精度评价指标。具体计算公式如下:
(3)
(4)

3 BP和GA-BP神经网络模型训练性能和预测结果分析
3.1 2种模型的训练性能
考虑到算法的随机性,将2个模型分别独立运行20次,并分析模型训练性能。2种算法的训练结果精度如表2所示。
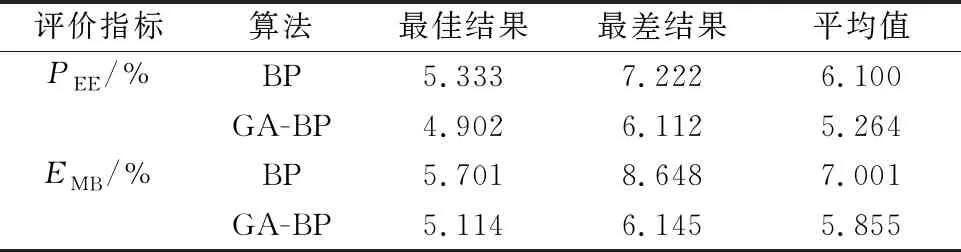
表2 2种算法的训练结果
通过对比表2中数据可知,BP模型的预测能力相对较差,其最差PEE和EMB可达到7.222%和8.648%,20次训练的平均PEE和EMB值分别为6.100%和7.001%。与之对比,由GA-BP模型训练得到的平均PEE值和EMB值分别减小0.836%和1.146%。通过对比2个模型的PEE及EMB的最佳值、最差值及平均值,也显示GA-BP模型相对稳定。因此,在大型CCHP冷负荷预测领域,GA-BP模型具有全局优化能力强、预测精度高等优点。
3.2 模型预测结果分析
随机选取2019年7月2日至10月8日中5天数据作为测试集,来检验模型的预测精度。预测结果如图5所示,预测精度见表3。

图5 2个模型预测值与真实冷负荷值对比

表3 BP和GA-BP神经网络预测精度对比 %
表3和图5中数据显示,无论BP神经网络模型还是GA-BP神经网络模型预测的结果,与冷负荷真实值的变化趋势都基本一致,BP神经网络模型预测值在部分时段误差较大。GA-BP神经网络预测期望误差百分比PEE和平均绝对误差EMB分别为5.86%和6.46%,明显低于BP神经网络。
将2个模型的预测值与实际值分别进行线性回归拟合,结果分别如图6和图7所示,GA-BP模型的拟合点除少部分点,特别是在低值段偏离y=x线外,大部分区域的偏差较BP神经网络小。
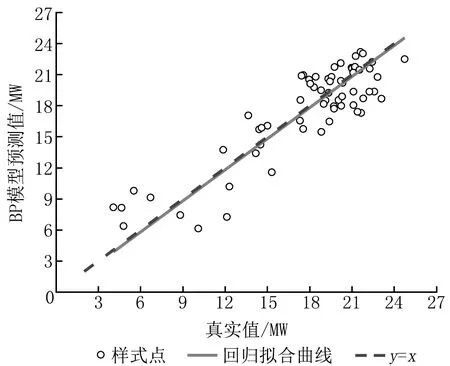
图6 BP模型预测值与真实值回归拟合曲线
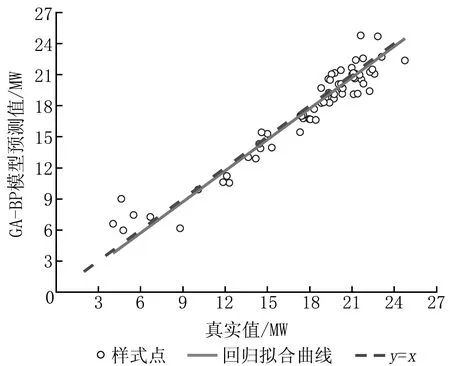
图7 GA-BP模型预测值与真实值回归拟合曲线
对绝对误差值进行比较分析,如图8所示,BP神经网络预测结果的绝对误差值大于2 MW的显著多于GA-BP神经网络预测结果,且随着冷负荷的增大,BP网络预测值绝对误差也显著增大,在相同条件下GA-BP神经网络预测绝对误差变化不明显。

图8 2种模型预测值与真实冷负荷值绝对误差
综上所述,GA-BP模型在预测大型CCHP负荷方面明显优于BP模型,更易获得逼近真实值的预测结果。
4 结论
为了实现对大型CCHP系统用户负荷更准确的预测,为智能化的优化运行提供重要的数据支撑,在利用Spearman秩相关系数对历史运行数据进行相关性分析的基础上,分别利用BP和GA-BP神经网络训练模型对随机选取的验证集进行了预测分析,主要结论如下:
1) 利用Spearman秩相关系数,确定影响大型CCHP系统冷负荷的主要因素,弱化或剔除次要因素,并将主要因素作为负荷预测模型的输入参数。相对于传统BP模型多变量输入,GA-BP模型可显著缩短模型训练时间,规避维数灾难,提高预测精度。
2) (T-1)时刻与T时刻的冷负荷的秩相关系数最大,空调冷负荷时间序列性很强;(T-24)时刻与T时刻的冷负荷的秩相关系数虽小于(T-1)时刻,但也达到接近0.6;室外风向和风速对冷负荷影响较小。
3) 经过遗传算法优化的BP神经网络的网络结构和模型参数,避免了局部收敛,实现了全局最优,可明显提高模型的预测精度。如本案例中GA-BP相对BP模型预测精度分别提高了37.12%和40.84%。
以上改进型BP神经网络,显著提高了预测大型CCHP系统空调负荷的准确性,为此类系统优化调配的人工智能化发展提供了新的思路。
