中深层地埋管换热器传热过程对周围岩土体的热影响
2021-03-16山东建筑大学贾林瑞方肇洪
山东建筑大学 贾林瑞 崔 萍 方 亮 方肇洪
0 引言
传统的地埋管地源热泵技术采用的钻孔深度通常为40~150 m,称之为浅层地热能利用技术,需要足够大的地表区域来布置钻孔,易受到地表面积的限制。为了扩大地源热泵的应用范围,提出了一种新的技术,钻孔深度可达到1 500~3 000 m,称之为中深层地埋管换热器技术[1]。这种技术不需要布置太多的钻孔,便可达到所需的供暖指标。对比发现,长期运行的浅层地源热泵系统可能具有明显的性能降级现象,而利用中深层地埋管换热器的独特技术优势可有效改善这种现象[2]。由于中深层地埋管换热器埋深较浅层地埋管换热器存在数量级的不同,地下岩土层在深度方向的温度梯度就不能忽略,其传热机理也更为复杂。
中深层地源热泵系统研究的核心问题在于地埋管与周围土壤之间的传热,这是一个较复杂的传热问题,涉及到岩土体和换热器2个部分。考虑到系统对管道强度及施工工艺等要求较高,采用性能更优的套管式换热器,套管截面见图1。使用套管式换热器可以显著提高地源热泵系统地下换热装置的换热效率,从而可以减少换热井设置数量、节省换热系统的占地面积、降低换热系统的初投资[3]。

注:R1为外管与钻孔壁之间的热阻,R2为内、外管间的热阻。
目前,关于中深层地埋管换热器的研究方法主要有数值解与解析解2种模型。数值解常用的方法就是运用CFD、FEFLOW等软件计算,如Renaud[4]、Lous[5]等学者的研究;除此之外还可以通过有限差分和有限元的方法编写程序求解,如Holmberg[6]、Morchio[7]等学者的研究。笔者所在的研究团队在已有浅层地埋管理论基础上,同时建立了解析解和数值解传热框架下的中深层地埋管换热器传热模型,并进行了理论和应用基础研究[1,8-9];随后在上述理论基础上提出了一种新的计算中深层地埋管换热器循环水温的解析解模型,经验证,其准确性高于传统的解析解模型[10]。除此之外,搭建实验台进行实验也是常见的研究方法,Song[11]、Wang[12]、Cai[2]等学者运用搭建的实验台研究了中深层地埋管换热器的循环水及岩土体温度的动态响应。目前还未发现相关文献对中深层地埋管换热器的热影响半径进行研究。
研究不同工况下地埋管换热器的热影响半径,对于中深层地埋管换热器的实际应用具有重要的意义。确定钻孔埋管群中钻孔之间的合理距离,可有效预防因热影响区域交叉造成热干扰而降低换热器的运行效率,此外对地下热环境也具有一定的保护作用。本文在以往研究成果的基础上,利用笔者建立的数值模型对中深层地埋管换热器的地下传热及其对周边岩土体温度的影响进行深入研究,分析不同工况下岩土体的温度响应规律,为中深层地源热泵系统的设计及实际应用提供参考。
1 中深层套管式地埋管换热器传热模型
1.1 模型计算假设条件
采用套管式换热器,以线热源理论为基础得到简化传热模型[13-15],理论研究中为了简化计算过程,仅取单个换热钻孔为研究对象。地埋管换热器的传热过程是一个复杂的、半无限大区域内的非稳态过程,实际计算较为复杂,因此假设:
1) 将地埋管换热器周围的岩土层看作一个或几个均匀介质的水平地层,忽略可能的地下水流动。
2) 忽略空气温度及大地表面温度随季节的波动。
3) 认为通过整个地层的大地热流是均匀的。
4) 管内流体介质的流动和传热采用一维模型,即忽略流道横截面上的循环介质的速度和温度分布。
5) 岩土体初始温度分布在径向上是均匀的。假设大地热流是均匀恒定的,在不同的水平地层(导热系数不同)有不同的温度梯度。
1.2 套管式地埋管换热器的传热模型
基于上述假设,该传热问题可近似看作轴对称的传热问题,岩土层的导热方程可写为
(1)
式中α为热扩散率,m2/s;t为温度,℃;τ为时间,s;r为岩土层半径,m;z为深度,m。
套管内流体温度的控制方程应考虑流体的流动方向。流动方向不同时,方程中对流项前的正负号也随之改变。以下方程中设定z坐标的方向向下。
流动方式为外进内出(从两管的夹层中向下流入,流体从内管流出)时,内外管流体的能量方程分别如下:
(2)
(3)
式(2)、(3)中C2为热流内通道单位长度的热容,J/(m·℃);tf2为出水水温,℃;tf1为进水水温,℃;C为循环液的热容流量,W/℃,C=Mc,其中M为质量流量,kg/s,c为循环水比热容,J/(kg·℃);C1为热流外通道单位长度的热容,包括循环液、外管壁和回填料的热容,J/(m·℃);R2为内管流体到外管流体之间的热阻,m·℃/W;R1为外管流体到钻孔壁的热阻,m·℃/W。
1.3 套管式地埋管换热器传热过程的数值计算模型
在求解以上能量方程时采用有限差分法。将中深层地埋管换热器整个传热区域沿径向及深度方向划分为若干个网格。进行径向网格划分时,根据热量传导的特点,采用变步长网格,径向扩大倍数Δσ为1.2,最小网格单元r0=rb=0.14 m,r0、rb分别为径向网格第一个网格节点和钻孔壁的半径;在深度方向上则均匀划分为200个网格节点,钻孔深度H=2 000 m。节点示意图见图2。
在建立节点差分方程时采用“元体热平衡法”,岩土体及流体的差分方程及初始条件、边界条件如下[2,9]。
1) 岩土体及流体的差分方程。
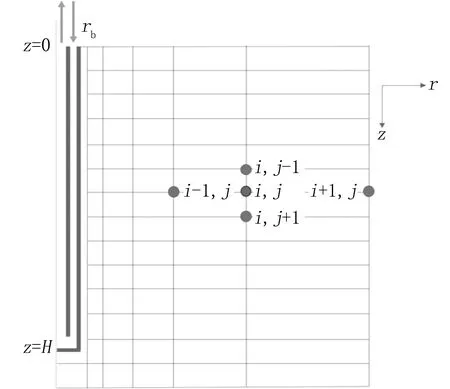
图2 差分区域离散化
(4)
式中 Δτ为时间步长,s;p代表不同时刻;Δz为深度方向离散距离,m。
对钻孔内部的流体沿流动方向也建立了相应的节点方程式,具体建立方法见文献[1,8]。
2) 初始条件与边界条件。
在均匀大地热流的假定条件下,根据能量守恒定律,在任意深度处地层中的初始温度可以表示为
(5)
式中ta为地表以上的空气温度,℃;qg为大地热流密度,W/m2;ha为地表的对流换热系数,W/(m2·℃);m为岩土分层的层数;λ为岩土体导热系数,W/(m·℃);Hj为第j层地层底部的坐标;rbn为数值模型径向边界尺寸,m。
对于固体岩土层中的导热问题,在距离套管中心足够远的径向边界r=rbn处设定为第一类边界条件,即认为边界上的温度在传热过程所涉及的时间内没有变化,即
(6)
同样地,传热区域的下边界设定在钻孔底部以下200 m的位置,此范围对于以30 a为周期的模拟是足够大的。当地埋管从土壤取热时,岩土温度逐渐降低,温降程度随着远离埋管逐渐减小,直至达到某一处后温降为零,此处的温度即为岩土层的初始温度,并以此作为计算边界,即定壁温边界条件。
地表边界设定为第三类边界条件,即假设地表以上的空气温度及对流换热系数始终保持不变。
(7)
将各点的平衡方程列出后得到整个求解区域的差分方程组,采用追赶法[14]求解方程组,即得到不同时刻岩土体的温度分布。
2 中深层地埋管换热器传热性能及热影响半径分析
2.1 热影响半径定义与参数的选择
为了更准确地描述不同取热状态下,埋管的持续取热对周围岩土体热环境的影响程度,引入热影响半径r*。
Δtr*,z,τ=tr*,z,τ-tr*,z,0
(8)
式中 Δtr*,z,τ为τ时刻半径为r*处的温度tr*,z,τ与该点处岩土初始温度tr*,z,0的差值。
当Δtr*,z,τ取值不同时,计算得到的热影响半径也不同。
理论研究中为了简化计算过程,仅取单个换热钻孔为研究对象,并将钻孔周围的岩土体看作一个均匀介质的水平地层,且忽略可能的地下水渗流。钻孔直径db取0.28 m,钻孔深度为2 000 m,地表温度为10 ℃,钻孔内布置套管式换热器,外管材料为钢管,内管选用高密度聚乙烯管,其余主要参数见表1。根据经验及初步计算可知,一个深度为2 000 m左右的钻孔,在一个供暖季120 d内的平均取热功率大约为150~250 kW。为保守起见,本文取150 kW的取热功率为计算依据。

表1 主要设计参数
2.2 地下岩土体温度热响应
本文仅讨论地埋管单取热工况的地下传热问题。假设一个供暖季连续取热120 d,每天运行24 h,地埋管的总取热功率为150 kW。根据上述数学模型可以计算出埋管周围岩土体在不同时刻不同位置的温度响应。图3显示了地埋管取热前的岩土体初始温度分布及系统运行20 a后地埋管周围岩土体温度分布。系统运行时,地埋管从周围岩土体取热,使周围岩土体温度降低。在图3可以看到,距离埋管越近,岩土体温度变化越大,但沿着半径方向最终趋于平稳,接近岩土体初始温度。当埋管换热器的取热负荷不同时,对周围岩土体热环境的影响程度也会不同。
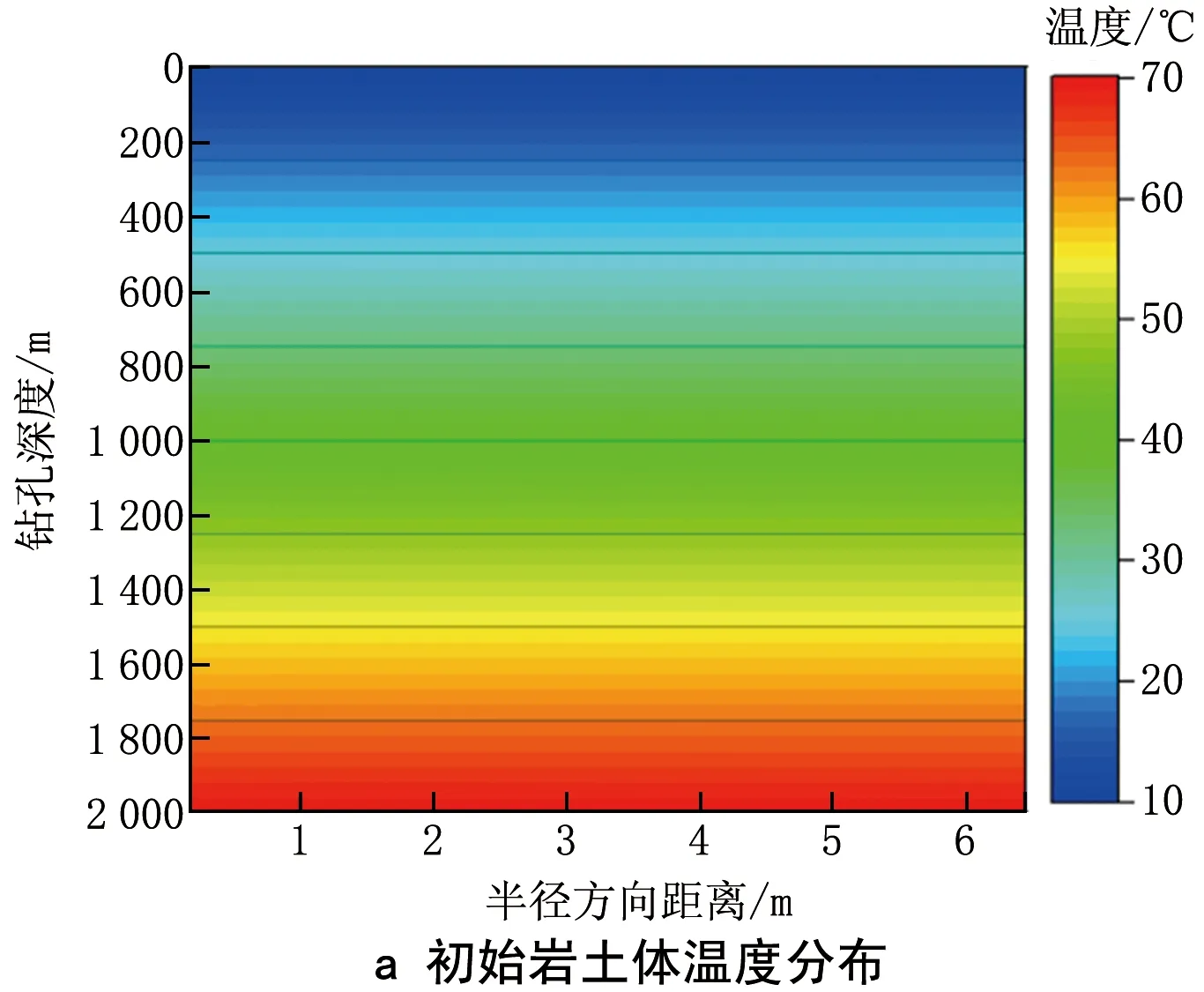
图3 地埋管周围岩土体温度分布云图
由于钻孔的有限深度及地表面边界条件的影响,地埋管换热在不同深度处引起的热影响半径是不同的。图4a显示了不同半径处在深度方向的温度分布,图4b显示了热影响半径沿深度方向的变化。可以明显地看到:在0~600 m深度范围内温降为负值,产生这种逆向传热现象的原因是在浅层换热区,从地埋管外管进入的循环水的温度高于周围浅层岩土体的温度,热量由循环水向岩土体传递,致使岩土体温度升高,高于初始温度;在600~1 900 m处,沿着深度方向土壤温度与初始地温的差值Δt逐渐增大,直到在1 900 m处达到最大值。温度变化率最快的地方热影响半径最大,在图4a中可以看到不同半径处的温度数据对深度求导的结果,1 400~1 800 m处的温度变化率最快。经过进一步计算发现,钻孔深度1 750 m处的热影响半径最大(见图4b),因此,可选用此处作为设计依据。
2.3 运行时间对热影响半径的影响
由非稳态导热机理可知,地埋管换热在半无限大岩土体内产生热影响半径的关键因素之一是传热时间。图5、6分别显示了地埋管换热10、15、20 a后沿半径方向的温降及热影响半径随时间的变化趋势。随着系统的运行,埋管不断从岩土层取走热量,靠近埋管处的温度降低,远处的热量向埋管方向传递,而且这种热量传递范围在空间上的尺度不断扩大,因此热影响半径增大。以温降0.5 ℃的岩土体位置为热影响半径判断依据,运行10、15、20 a后的热影响半径分别为40.98、51.02、51.22 m。从第15年到第20年热影响半径仅增加了0.20 m。因此可定性判断,20 a后岩土体温度分布基本处于稳定状态,热影响半径也基本不再扩大。
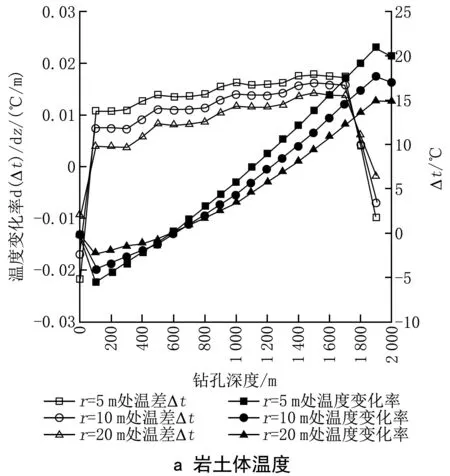
图4 岩土体温度及热影响半径沿钻孔深度方向的分布

图5 运行时间对温降Δt的影响

图6 热影响半径随运行时间的变化
不同地区的供暖期长短不一,与气象参数关系较大,气象参数对地表温度的影响较大,本文研究的重点是岩土层中的最大热影响半径,其深度约为1 750 m。经过验证后发现,地表温度的变化对热影响半径的取值基本没有影响,为了简化计算,选取平均温度。为了研究不同供暖期时间对热影响半径的影响,取3个工况,每年运行2 160 h(3个月)、2 880 h(4个月)、3 600 h(5个月)。图7、8分别显示了运行20 a后沿半径方向的温度变化及热影响半径随供暖季运行时长的变化。由图8可以看出:随着每年供暖季运行时长的增加,热影响半径逐渐增大,且基本呈线性增加。表2显示了运行20 a后不同运行工况下热影响半径取值。可以看出,全年取热对地下热环境的危害极大,不利于土壤温度场的恢复,且持续运行与实际情况不符,但在未确定供热期长短时可将此值作为设计参考值使用。
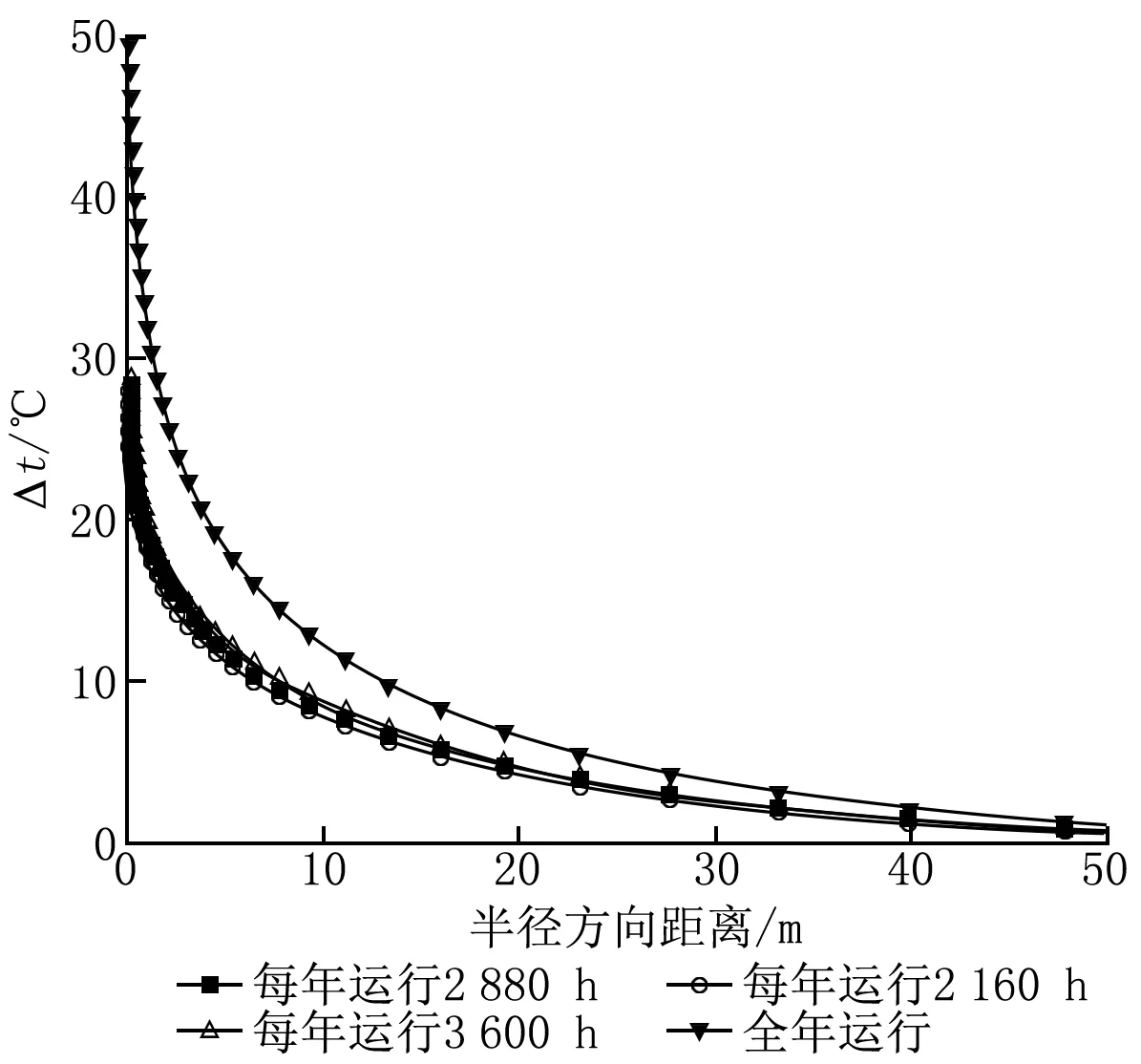
图7 运行20 a后沿半径方向的温度变化
图8 热影响半径随供暖季运行时长的变化
表2 运行20 a后不同运行工况下热影响半径取值(Δtr*,z,=0.5 ℃)

表2 运行20 a后不同运行工况下热影响半径取值(Δtr*,z,=0.5 ℃)
每年运行时间/h热影响半径/m2 16051.002 88051.223 60052.88全年运行59.89
2.4 取热负荷对热影响半径的影响
影响地埋管换热器热影响半径的另一个关键因素是地埋管的取热强度。图9、10分别显示了不同取热负荷时径向温度的变化及热影响半径随取热负荷的变化。由图9可以明显看出,随着取热负荷的增大,岩土体温差Δt相应增大,但是沿半径方向,不同负荷间的差值越来越小。由图10可以发现,热影响半径与取热负荷基本上呈线性关系。当Δtr*,z,=0.5 ℃,系统运行20 a后,50、150、250、350 kW取热负荷下的热影响半径分别为49.74、51.22、55.60、57.38 m。

图9 不同取热负荷Q时沿半径方向温度变化

图10 热影响半径随取热负荷的变化
3 基于热影响半径的多孔换热下单孔名义取热量
在实际工程应用中,由于供热负荷的不同,往往需要设置多个钻孔作为供热热源,多个钻孔之间的热干扰使热影响区域的传热分析更加复杂。因此,下文主要研究多根埋管共同运行时,埋管与埋管之间的相互影响程度及热影响半径在实际中的应用。
引入名义取热量Qm[1],即在特定运行工况下1个深层钻孔可以提供的最大取热量。
在本文中特定工况指的是:1) 取热量在运行的20 a间是恒定的;2) 地埋管换热器的进口温度在取热期间不得低于5 ℃;3) 岩土层的初始温度分布是预先确定的。
以3×3的埋管布置形式为例,布置示意图见图11。由图11可以看到,埋管群中有3种位置的埋管:中心处(1#);45°(2#)、135°、225°、315°处的埋管;0°、90°(3#)、180°、270°、360°处的埋管。很明显,运行最不利的是1#埋管,3#埋管次之,2#埋管最好。

注:L为埋管间距。


图随埋管间距的变化(运行20 a后)

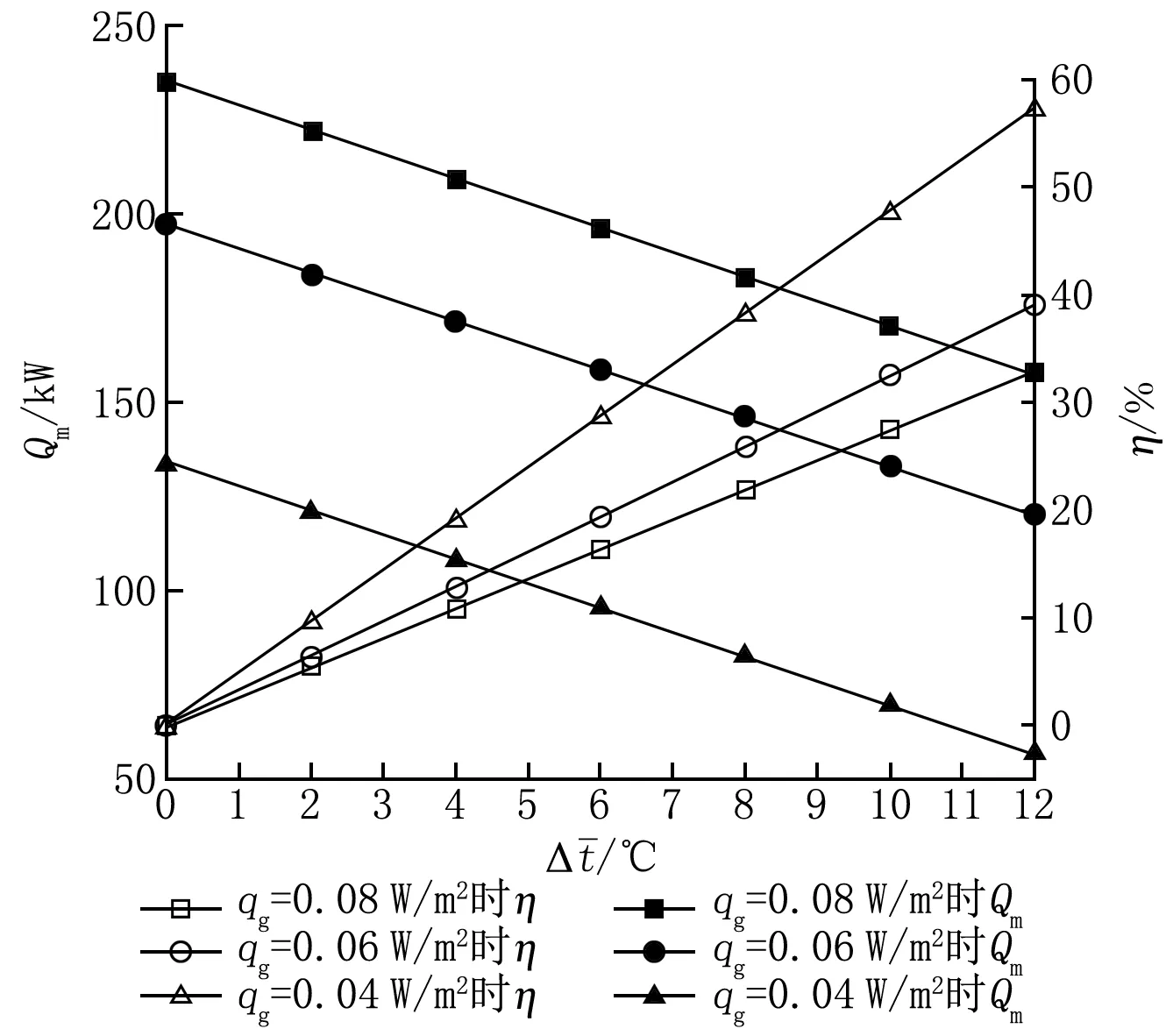
图13 名义取热量和误差η随的变化
η的计算式为
(10)

4 结论
1) 经计算,当取热负荷为150 kW、钻孔深度为2 000 m时,热影响半径最大值出现在1 750 m深处,而非钻孔底部或中部。
2) 影响热影响半径取值的主要因素包括取热负荷和运行时间,并与负荷强度及传热时间成正相关。运行20 a后,热影响半径基本不再变化。
3) 当采用3×3布置形的钻孔群取热时,建议钻孔间距大于100 m,此时名义取热量损失率小于5%。
