一种鲁棒GPS/INS组合导航滤波算法设计
2021-03-16王伟丛宁邬佳
王伟, 丛宁, 邬佳
(哈尔滨工程大学 智能科学与工程学院,黑龙江 哈尔滨 150001)
GPS/INS组合导航系统能够充分利用2种导航系统的优点进行互补,具有高精度、高可靠性的特点,在动态定位领域获得了极为广泛的应用。GPS/INS中常用的滤波方式主要是卡尔曼算法[1-3],但该算法会出现过于依赖噪声特性准确性的情况,鲁棒性较差,有诸多学者对其进行了研究和改进。文献[4]提出了基于协方差匹配技术的自适应UKF算法,解决了惯性器件和GPS的噪声分布不准确时UKF的精度下降的问题。文献[5]提出的自适应鲁棒CKF,应用马氏距离减弱了异常量测值对估计的影响,一定程度上增强了系统的鲁棒性。文献[6]提出一种改进的自适应扩展卡尔曼滤波算法,该算法可以基于残差实时估计系统噪声。但当系统噪声或量测噪声不确定,再或初始条件不具备时,上述Kalman衍生算法均不能实现精确估计。
为解决上述问题,Shmaliy等[7]提出了一种在滤波过程中能够无视噪声统计特性的无偏有限冲击响应滤波算法(unbiased finite impulse response filter, UFIR)。该算法在不明确系统噪声、量测噪声的统计特性且初始条件未知的情况下,仅利用最佳窗口长度1个参数就能对系统做出精确估计。最佳滤波窗长的大小会影响滤波精度和运算时间。为了提高确认最佳滤波窗长的效率,文献[8]提出一种在线估计方法,但该方法没有实现真正的在线估计,影响系统的实时性。且由于UFIR自身的滤波原理所限,其导航精度要略差于卡尔曼滤波及其衍生滤波。
针对上述问题,本文将UFIR应用于GPS/INS组合导航系统中,提出一种级联式导航滤波器,设计一种在线估计最佳窗口长度算法的同时,引入了级联自适应卡尔曼滤波器以提高滤波器的导航估计精度。
1 UFIR及其改进算法
1.1 UFIR算法
设系统状态方程和量测方程为:

(1)
式中:X(t)为系统状态矢量;F(t)为状态转移矩阵;W(t)为系统噪声矢量;Z(t)为量测矢量;H(t)为量测矩阵;V(t)为量测噪声矢量。
离散后为:
(2)
式中:Xk表示第k时刻的系统状态矢量,即X(t),同理,Zk为Z(t),Wk为W(t),Vk为V(t),Fk为F(t)。当已知第k时刻的量测时,利用从m=k-N+1时刻到k时刻的N组量测可以实现对k时刻的系统状态估计。
1.1.1 滤波过程
UFIR不需要设置噪声协方差矩阵和初始误差,它以最佳滤波窗长代替了上述初始条件。在最佳滤波窗长下获取的估计值具有最小的均方误差(the mean-square error, MSE)。UFIR算法从k-N+1时刻开始通过滤波获得估计值,且通过并行计算降低了窗口滤波的运算量,不需要为获得某一时刻的估计值而重复运行N遍。对上文中建立的状态空间模型进行扩展[9]
(3)
将状态转移矩阵作如下扩展:
(4)

本文中观测矩阵Hk为时不变矩阵,可简化表示为H,故H的状态扩展可表示为:
(5)

与卡尔曼滤波原理相似,UFIR滤波也利用类似的思想,令UFIR增益为[10]:
(6)
(7)
则:
(8)
1.1.2 批处理过程
UFIR滤波初始条件由批处理滤波获得:
(9)
(10)
式中s=m+M-1,M为批处理窗长。
由上述推导可看出,滤波窗长N的大小决定了矩阵的维数,同时也决定了UFIR算法的运算速度,而找出算法的最佳滤波窗长是滤波的前提。
1.2 在线估计设计与实现
UFIR滤波器是一种窗口滤波器。虽然在使用中不需要提供初始状态向量、初始协方差矩阵、系统噪声和量测噪声的统计特性,但需要对其滤波窗口大小N进行估计。N越大,估计效果可能越好,但同时运算量急剧增大;N过小,达不到要求的滤波精度。所以最佳滤波窗长的在线估计是UFIR滤波算法的重点。
本文对文献[8]中提出的在线估计方法进行了改进,提出了一种适用于时变系统的在线估计最佳滤波窗长算法。为保证滤波性能只与滤波窗长N有关,将批处理窗长M设为定值(批处理窗长M≪N)。
1.2.1 确定Nmin和Nmax
为了能够更快的确定最佳滤波窗长,首先需要确定窗长的变化范围。现有方法中窗长的范围一般为经验值,不能适应不同条件下的需求,且若给定的范围过大,则影响运算速度,范围小则不能包含最佳滤波窗长。
针对上述情况,本文设计了详细的运算步骤来计算范围Nmin和Nmax,主要包括下列2个阶段:

(11)
(12)

(13)
Gk=tr(MN)
(14)
(15)

取Nmin和Nmax之间的整数对剩下的数据进行处理。范围内的每个N都会对剩余n-L+1组(n>L)数据进行1次UFIR滤波处理,每σ组数据为一批次(σ为滤波窗口大小N与批处理窗口大小M的差值)。
(16)
再利用lN|m可得:
(17)
(18)
(19)
(20)

2 级联滤波算法设计
与KF算法不同,UFIR不是最优估计,由于自身的滤波原理所限,在系统噪声特性变化不大时,其滤波精度略低于卡尔曼算法。为了兼顾系统的鲁棒性和精度,本文提出一种级联式GPS/INS导航滤波算法。图1为INS/GPS组合导航系统的原理框图。GPS为系统提供速度、位置和航向信息:速度位置与惯导解算出的速度位置之差作为主滤波器改进UFIR算法的量测,继而通过主滤波器对速度和位置信息进行校正;将通过加速度计和GPS航向信息获得的姿态与惯导解算出的姿态之差作为从滤波器的量测,再利用主滤波器的新息、UFIR增益等信息获得自适应因子,通过从滤波器完成对姿态信息的校正。
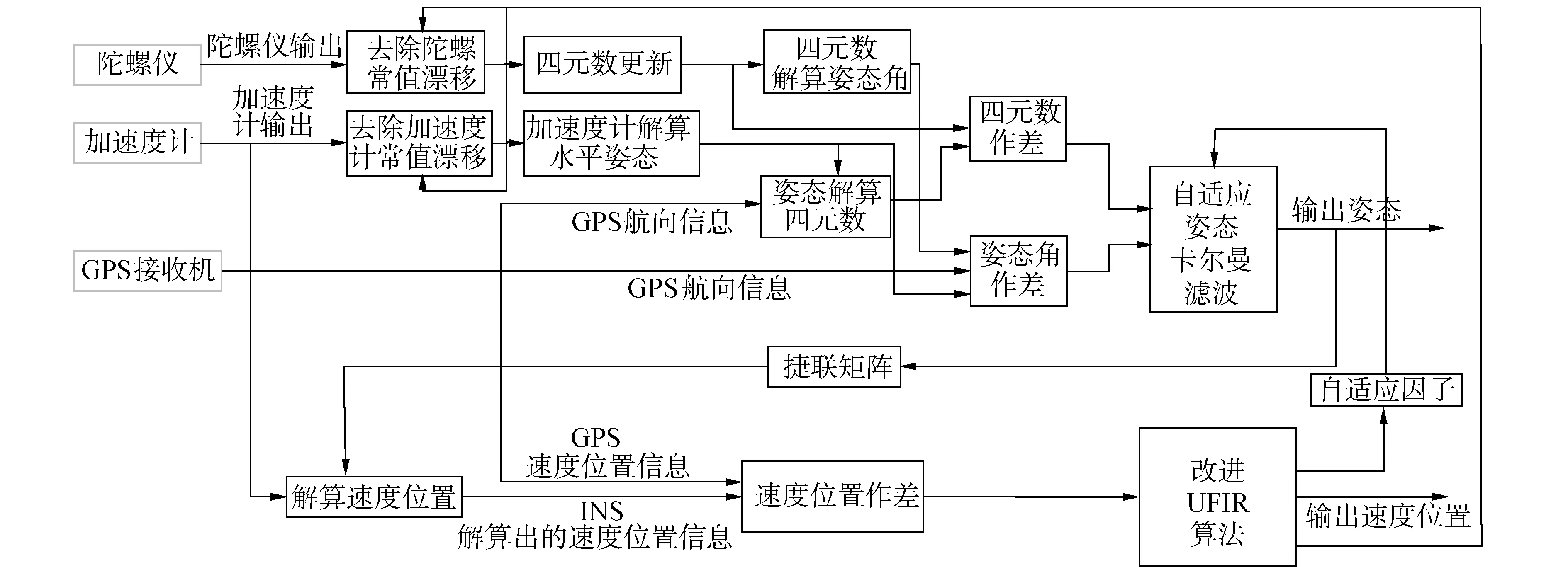
图1 INS/GPS组合系统原理Fig.1 INS/GPS integrated system block diagram
2.1 主滤波器设计
采用间接法建立状态方程,INS选取东北天坐标系作为导航坐标系。
选取系统的状态量:

(21)
取速度位置差值作为观测量:
(22)
相关参数变量见文献[13],这里不再赘述。
2.2 从滤波器设计
从滤波器状态方程为四元数误差线性微分方程,将姿态角误差作为量测量,量测方程利用四元数误差与姿态角误差之间的转换关系得到。
2.2.1 滤波算法模型
通过加性四元数误差微分方程整理出的状态方程为:
(23)

观测量设为加速度计与双天线GPS航向构成的姿态角与惯导系统解算出的姿态角之差:
(24)
而上述姿态误差角不能直接当成观测量使用,需要利用变换矩阵将其转换为数学平台失准角才可用于导航滤波。
利用四元数与旋转角的关系可知:
(25)
(26)

(27)
式中va(t)为量测白噪声。
2.2.2 自适应性改进
本文将UFIR(主滤波器)的新息引入自适应渐消因子ck[16-17]中,对级联卡尔曼滤波器的从滤波器进行改进:

(28)
式中β为调节因子。
利用式(28)对自适应卡尔曼滤波增益方程进行优化(具体卡尔曼算法流程见文献[13]):
Kk=ckPk|k-1HT[HPk|k-1HT+Rk]-1
(29)
3 仿真评估与分析
通过仿真计算和实验验证对提出的导航滤波算法性能进行了评估,并与文献[6]中提出的改进型自适应扩展卡尔曼滤波算法和最佳滤波窗长下的标准UFIR算法进行了比较。
3.1 仿真计算


图2 仿真轨迹Fig.2 Simulation trajectory
采用增大仿真轨迹的噪声方差的方式来验证级联式GPS/INS松组合导航滤波器在系统噪声和量测噪声统计不准确的情况下的滤波性能。在500~1 000 s,将系统噪声标准差增大10倍,在1 000~1 500 s,将系统噪声标准差增大20倍,在1 500~2 000 s,将系统噪声标准差增30倍,在2 000~2 500 s,将系统噪声标准差增大50倍,在2 500 s之后的时间段,将系统噪声的标准差增大100倍。



图3 最佳滤波窗长曲线Fig.3 The line of optimal filter window length

图4 速度误差仿真曲线Fig.4 Velocity error simulation curve

图5 位置误差仿真曲线Fig.5 Position error simulation curve
3.2 实验验证
通过跑车实验验证CUFIR的实用性,跑车轨迹见图6。
车载INS/GPS组合导航系统包括1套型号为ADIS16488的MEMS和1台LEA-M8S GPS接收机,INS数据更新频率为205 Hz,GPS更新频率为5 Hz。跑车实验的真值由RTK提供。由于车载导航设备受外界环境的影响较大,故其系统噪声统计特性虽会发生变化,但变化幅度会小于仿真所设计的情况。

图6 跑车轨迹Fig.6 The actual driving test route


图7 实测速度误差曲线Fig.7 Measured velocity error curve
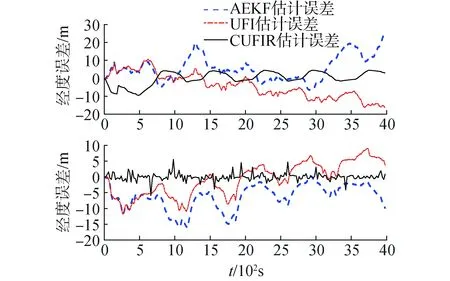
图8 实测位置误差曲线Fig.8 Measured position error curve
4 结论
1)提出的估计最佳滤波窗长的方法能有效地实现窗长的在线估计。
2)通过仿真与实测,级联滤波算法CUFIR能有效提高滤波精度,增强系统的鲁棒性。
